T形截面屈曲约束支撑力学性能的影响因素分析

王永贵, 谢晓杰

(1.河南理工大学 土木工程学院,河南 焦作 454000; 2.郑州工业应用技术学院,河南 郑州 451100)



T形截面屈曲约束支撑力学性能的影响因素分析

王永贵1, 谢晓杰2

(1.河南理工大学 土木工程学院,河南 焦作 454000; 2.郑州工业应用技术学院,河南 郑州 451100)

文章探讨了T形截面屈曲约束支撑构造参数对其力学性能的影响,借助ANSYS有限元分析软件,通过APDL语言二次开发,对外围约束机制为矩形钢管混凝土的屈曲约束支撑受力机理进行分析;系统研究了约束刚度、初始缺陷、宽厚比、间厚比、应变强化及摩擦力等因素变化对支撑力学性能的影响。研究表明,随约束刚度的增大,芯材初始缺陷的影响呈降低趋势,保证屈曲约束支撑稳定工作的最小约束比为2.0;间厚比介于0.05～0.1之间时,支撑的承载力没有明显变化;增大芯材截面厚度、合理控制间厚比取值及降低芯材初始缺陷均有利于降低摩擦力的影响。

屈曲约束支撑;有限元;力学性能;影响因素

为降低结构的振动响应,减轻地震灾害,研究人员对消能减震理论及其应用技术进行了深入研究[1]。屈曲约束支撑通过外围约束单元抑制内部芯材在轴向荷载下产生屈曲失稳现象,不仅起到普通支撑的作用,而且其滞回曲线饱满,可明显改善支撑框架结构体系的延性和抗震性能,已日益受到关注[2-3]。

但是,现有的屈曲约束支撑技术大多来自国外,为实现屈曲约束支撑的标准化及国产化,研究人员在屈曲约束支撑的构造设计、理论分析及抗震性能等方面展开了研究[4]。文献[5]对全钢屈曲约束支撑的局部稳定性进行了研究,结果表明,约束比和厚度比、间隙大小、轴向变形等是影响全钢屈曲约束支撑局部稳定的主要因素。文献[6]对双矩管装配式屈曲约束支撑进行了理论分析,提出了外围约束单元刚度折减系数的计算公式。文献[7]提出了一种钢板装配型开孔式屈曲约束支撑,支撑的芯材及约束机制均为钢板,为实现特定的耗能效果,芯材钢板上设计有开孔,并分析了其力学性能。文献[8]对芯材截面为一字形的屈曲约束支撑进行了有限元分析,主要对低周疲劳性能及多波屈曲模态进行了分析,结果表明,芯材的多波屈曲是导致屈曲约束支撑低周疲劳性能变小的关键因素。

上述分析中均探讨内核芯材截面为双轴对称的情形,对于内核芯材为单轴对称截面的屈曲约束支撑,相关研究较少,文献[9]对T形截面屈曲约束支撑进行了有限元静力分析,指出在轴向压力下支撑芯材的危险截面,未分析构造参数等因素变化对支撑力学性能的影响。为丰富屈曲约束支撑的产品类型,推广其工程应用,有必要对内核芯材为T形截面的屈曲约束支撑的构造要求及其力学性能进行分析。

本文根据非线性理论,借助ANSYS有限元分析软件,探讨了内核芯材截面为T形、外围约束机制为矩形钢管混凝土的屈曲约束支撑构造参数变化对支撑力学性能的影响。通过对不同有限元模型的分析,讨论了包括约束刚度、初始缺陷、

宽厚比、间厚比、应变强化及摩擦力在内的多种因素对支撑极限承载力的影响，为屈曲约束支撑的整体优化设计和细部构造改进提供理论参考。

1 屈曲约束支撑的力学分析模型

屈曲约束支撑在拉压状态下均能实现全截面屈服而不屈曲是其区别于普通支撑的显著特点。屈曲约束支撑可采用Plastic-Wen塑性单元进行模拟,该模型可用(1)式、(2)式表述[10],即

(1)

(2)

2 有限元模型的建立

2.1 试件参数

研究过程中内核芯材截面保持不变,通过调整外围约束机制的截面尺寸及间隙大小等参数,分析支撑的特征值及极限承载力等的变化规律。内核芯材工作段长度为2 000 mm,试件核心段屈服承载力为463 kN,其他参数见表1所列。

表1 屈曲约束支撑试件部分参数

注：h、b、t1、t2分别为T型钢核心段截面参数,单位为mm;B为外围约束机制截面宽度,H为外围约束机制截面

高度,T为外包钢管管壁厚度,B、H、T的单位为mm;E1I1、EcIc、EsIs分别为芯材、混凝土、外包钢管的抗弯

刚度;Pcr为支撑欧拉承载力;Pu为支撑极限承载力;Fy为芯材屈服承载力;ζ为支撑约束比。

2.2 材料定义

屈曲约束支撑的主要材料为钢材与混凝土,内核芯材及外包钢管均为国标Q235,内填混凝土强度等级为C30。钢材为理想的弹塑性材料,遵循Von Mises屈服法则及随动强化法则,弹性模量Es为2.06×105MPa,泊松比为0.3。混凝土遵循Von Mises屈服法则、相关流动法则、多线性随动强化法则及William-Warnke五参数强度破坏法则,初始弹性模量Ec为3.0×104MPa,泊松比为0.2。

2.3 单元定义

屈曲约束支撑通过内核芯材的塑性变形来耗散地震能量,芯材需具有塑性、大应变及大变形的性能,选取SOLID45单元进行模拟,该单元具有8个节点,每个节点有沿着x、y、z3个方向的自由度。屈曲约束支撑工作时,外包矩形钢管受到垂直于其平面的侧向荷载作用,具有板壳结构性质,且钢管不允许出现弹塑性变形,选取SHELL181单元进行模拟,该单元具有4个节点,每个节点具有6个自由度,即节点x、y、z方向的平动及绕x、y、z轴的转动。内填混凝土与外包钢管一起为内核芯材提供侧向约束,在轴向荷载作用下,内填混凝土有压溃和拉裂的可能,通过SOLID65单元进行模拟,该单元由8个节点进行定义,每个节点有沿着x、y、z3个方向的自由度。屈曲约束支撑芯材和外套管之间存在着接触关系,为面与面接触,采用接触单元CONTA173和目标单元TARGE170分别模拟内核单元和外围约束单元的面与面之间接触关系,接触单元CONTA173浮着在芯材表面,目标单元TARGE170浮着在约束外套管内表面,通过相同的常数形成接触对。接触单元不能穿透目标面,但目标面可以在满足位移容差的基础上穿透接触面。接触刚度越大,穿透位移越小,计算精度越好,但是会遇到计算收敛困难,因此需要综合考虑结构精度和计算效率来确定接触刚度。

2.4 网格划分

根据屈曲约束支撑的工作原理,分析时为使内核芯材与内填混凝土出现相对位移,其间设置接触对进行模拟;混凝土与外部矩形钢管不允许出现相对滑移,其接触部分完全黏结。支撑网格划分如图1所示。

图1 支撑分析模型网格划分

2.5 加载方式

本文采用单调加载模式,只在内核芯材端面施加相应面荷载,分析支撑在轴向荷载作用下的材料微观力学性能及试件的宏观力学特征。

2.6 边界条件

为使分析模型与试验情况及工程实际相吻合,分析时,模型两端铰接,轴向荷载施加于耦合节点上。外围约束机制端部及顶部自由,允许内核芯材与外围约束机制之间有相对位移。

3 影响因素分析

3.1 约束刚度

在轴向压力作用下,屈曲约束支撑为实现芯材的塑性变形,外围约束机制需为芯材提供足够的侧向约束,因此,外围套管应具有一定的抗侧刚度。此时,该抗侧刚度被称为约束刚度,通常用约束比来表示[11],计算公式为:

(3)

其中,Pcr为外围约束套管的屈曲荷载,与外套管的截面尺寸、套管长度及材料性质有关;Fy为内核芯材的截面屈服荷载,与芯材的截面面积及材料性质有关。

在分析约束刚度影响时,支撑的轴向应变限值为0.02,间隙厚度为1 mm,且不考虑芯材初始弯曲的影响,支撑极限承载力与约束比的变化关系如图2所示，不同轴向应变下的支撑极限承载力与约束比的变化关系如图3所示。

图2 支撑极限承载力与约束比变化关系

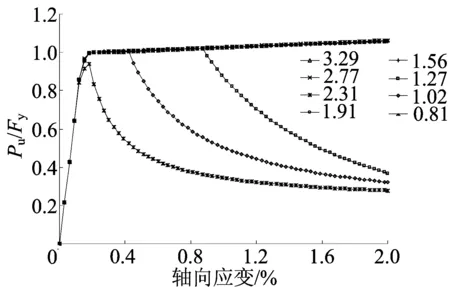
图3 不同轴向应变下支撑极限承载力与约束比变化关系

由图2、图3可以看出,约束比较小(ζ<1)时,内核芯材不能实现全截面屈服;随着外围套管约束刚度的增大,支撑的极限承载力渐趋稳定,并最终实现全截面屈服而耗能;当约束比超过某一限值(ζ=1.56)时,约束比的增加对支撑极限承载力的提高不产生明显影响。

不同约束比情况下的外包钢管相对挠度及其应力变化关系如图4所示。

图4 支撑外包钢管相对挠度及其应力与约束比的变化关系

由图4可以看出,约束比较小时,外围套筒中部的挠度较大并且应力分布极不均匀,此时内核芯材出现低模态屈曲,不利于支撑的整体稳定;随着约束比的增大,挠度及应力下降速率明显加快,且应力分布较为均匀,此时芯材与外套筒之间的接触点数目较多,支撑实现由低模态向高模态的转变,芯材的屈服面增多。

综上所述,约束比是影响屈曲约束支撑性能稳定发挥的关键因素,保证支撑稳定发挥其减震性能的最小约束比为1.51,考虑到其他因素的影响及给予结构一定的安全储备,建议屈曲约束支撑的约束比下限值为2.0,基于经济因素及结构自重考虑,约束比上限值为3.0。

3.2 内核芯材初始缺陷

屈曲约束支撑在加工制作及施工安装时,均对芯材的几何形状产生不同程度的影响,使芯材受荷之前就有一定的初始几何缺陷。芯材初始缺陷为0.001、0.002、0.005及0.010时的支撑极限承载力与轴向位移之间的变化关系，如图5所示。

图5 系列支撑极限承载力与初始缺陷的关系

由图5可知,初始缺陷使T形截面屈曲约束支撑的极限承载力下降,严重影响着支撑的耗能性能;外围约束刚度较小时,支撑对初始缺陷较为敏感,当约束刚度达到一定值时,初始缺陷对支撑性能已不产生影响。由图5a可见,试件TB-3(约束比为1.27)在0.001初始缺陷下,极限承载力在轴向应变超过0.9%时开始下降;0.002初始缺陷下,极限承载力上升趋势仅维持到0.6%的轴向应变;0.005及0.010的初始缺陷下,极限承载力低于屈服荷载,内核芯材不能实现全截面屈服。随着约束刚度的增加,不同初始缺陷下的屈曲约束支撑极限承载力渐趋稳定。由图5b可见，试件TB-4(约束比为1.56)在0.002初始缺陷下,轴向应变为2%时可实现全截面屈服;由图5c可见,试件TB-5(约束比为1.91)在0.005的初始缺陷下,轴向应变为2%时可实现全截面屈服,但在0.010初始缺陷下,在轴向应变超过0.5%时,极限承载力开始呈下降趋势;由图5d可见,试件TB-6(约束比为2.31)已对初始缺陷不敏感,在0.010初始缺陷下仍可实现全截面屈服。

支撑在0.010初始缺陷下的荷载位移变化规律如图6所示。由图6可知,即使在较为严重的初始缺陷下,随着外围约束刚度的增加,屈曲约束支撑由较低荷载下的屈曲失稳逐渐过渡为内核芯材的全截面屈服。

图6 0.010初始缺陷下支撑极限承载力

不同初始缺陷下的支撑临界约束比如图7所示。

图7 不同初始缺陷下的支撑临界约束比

由图7可知,支撑的临界约束比均随芯材几何初弯曲变大而非线性变大,初始缺陷为0.001、0.002、0.005及0.010时的临界约束比分别为1.343、1.415、1.622及1.986。

通过上述分析可知,随着初始缺陷的增大,屈曲约束支撑稳定工作的需求约束刚度亦随之增大;为保证屈曲约束支撑具有稳定的工作性能,建议约束比下限值取2.0。

3.3 芯材宽厚比

内核芯材的宽厚比指芯材翼缘宽度与其厚度之比,是屈曲约束支撑设计控制的要点。具有过大宽厚比的芯材,即使在合理间隙值及约束比情况下也可能出现局部受压屈曲失稳,进而影响支撑的耗能性能。现仅就TB-7试件进行分析，芯材截面面积、间隙厚度及外围套管截面尺寸均不变,仅调整芯材截面的宽度与厚度。宽厚比分别为5、10、15、20时的支撑极限承载力变化曲线如图8所示。

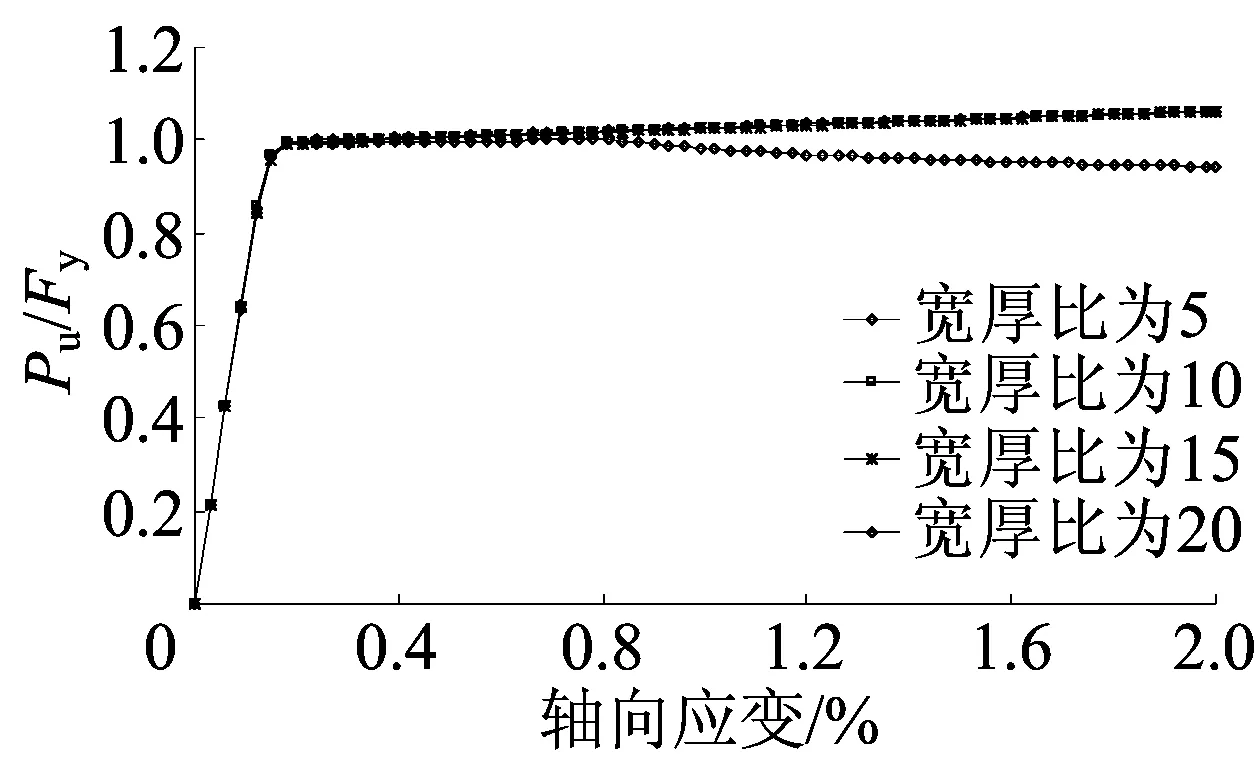
图8 芯材宽厚比变化与极限承载力关系

由图8可知,宽厚比控制在15以内时,试件的极限承载力随宽厚比的变化没有明显差异,在轴向应变为2%下均不出现下降趋势,可实现全截面屈服;当宽厚比为20时,在较小的轴向应变情况下,试件极限承载力的大小及其变化趋势与其他3个工况相同,但是,当轴向应变超过0.8%时,极限承载力呈现下降的态势,在轴向应变为2.0%时,试件极限承载力已降至屈服荷载的94.3%。这说明宽厚比过大时,试件在经历一定的变形后承载力降低,此后的过程均不能实现芯材的全截面屈服。

不同轴向应变下的支撑临界宽厚比如图9所示。分析表明,随着芯材轴向应变的增大,其临界宽厚比呈降低趋势,但降低趋势变缓。

图9 不同轴向应变下的临界宽厚比

3.4 间厚比

内核芯材与外围约束机制之间的间隙是屈曲约束支撑稳定工作的重要保证,是屈曲约束支撑重要的设计参数。内核芯材在轴向压力下因材料的泊松效应而出现横向变形,为有效防止横向变形对外围约束机制的挤压作用,需根据芯材的截面尺寸合理选择间隙厚度。定义间隙厚度与对应芯材截面厚度的比值为间厚比。当间厚比过大时,在轴向荷载作用下,由于缺乏足够的侧向约束,芯材出现半波甚至多波屈曲失稳而不能实现全截面屈服,降低支撑的滞回性能;如果间厚比较小,在轴向荷载作用下,芯材正常的横向变形被约束,使芯材由轴向受压演变为三向受力,支撑的极限荷载明显高于屈服荷载,但同时由于芯材的挤压,外围约束机制易产生横向裂纹而破坏,影响其约束能力,也降低支撑的抗疲劳能力。现以TB-7试件为例进行讨论,其中内核芯材截面尺寸、外围约束套筒截面尺寸均不变,仅改变间隙大小。间厚比分别为0.001、0.05、0.1、0.5、1.0时的支撑极限承载力变化如图10所示。

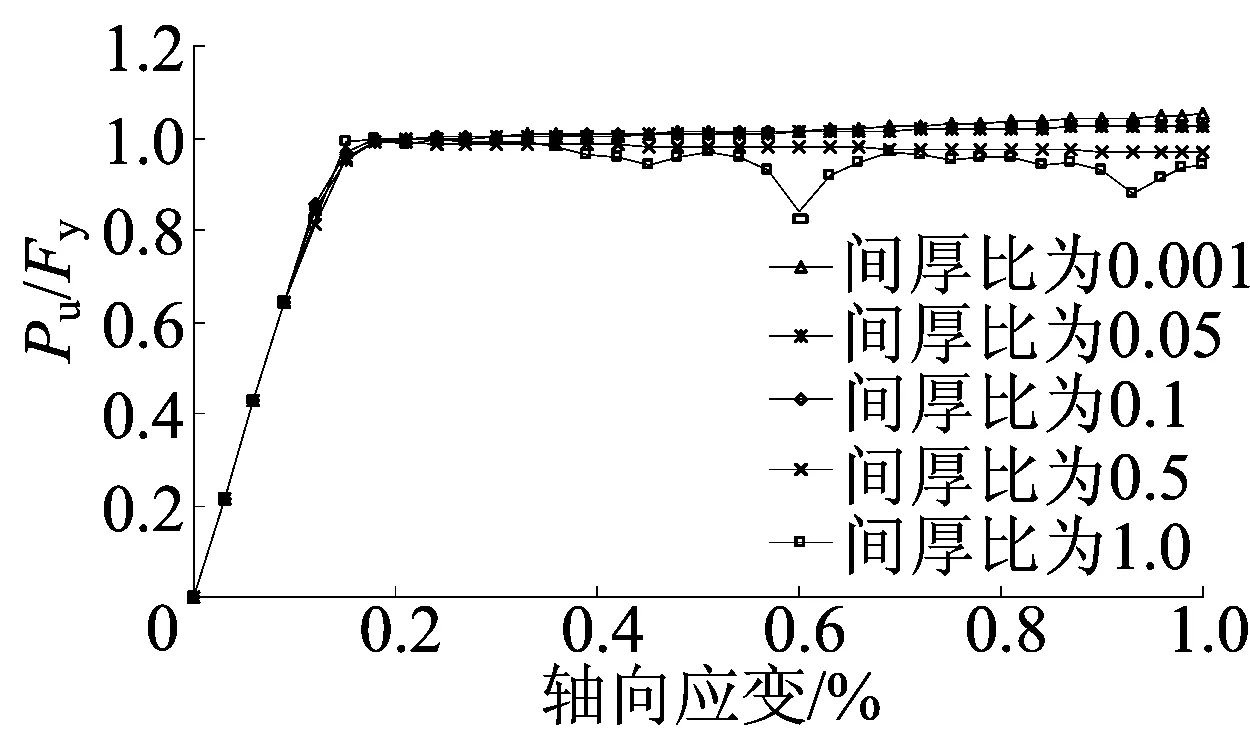
图10 间厚比变化与极限承载力关系

由图10可以看出,间厚比为0.001工况下,在轴向应变达0.6%时,支撑承载力开始出现明显增大趋势,轴向应变达1.0%时芯材压应力超过间厚比为0.1工况时的10%,同时可发现0.001工况时外围混凝土裂缝沿全长均匀分布;间厚比为0.5工况下,承载力在轴向应变为0.3%时开始下降,在1.0%轴向应变时,芯材压应力是间厚比为0.1工况的94.5%;间厚比为1.0工况下,当芯材轴向应变超过0.2%时,支撑承载力整体呈下降趋势,并且中间出现极值点,说明在该应变时接触突变,波形出现变化。分析表明,间厚比为0.05～0.1时,支撑的承载力及取值没有明显变化,且滞回性能较为稳定。

3.5 应变强化

上述有限元分析均假定内核芯材为理想的弹塑性材料。工程中所用钢材均为非理想的弹塑性材料,受力过程中产生应变强化现象。为分析钢材应变强化对支撑性能的影响,定义强化因子Ω[12]为:

(4)

其中,fm为钢材强化后的应力;fy为钢材的屈服应力。强化因子与试件的加载模式及变形过程无关,反映了钢材在某一时刻的应变强化程度,表明钢材内部结构的蠕变。现以TB-7试件为例,分析试件在不同强化因子下的约束比临界值变化情况,如图11a所示。为反映临界约束比随强化因子的变化关系,定义临界约束比强化系数ρζ[12]为:

(5)

其中,ζ0,Ω为强化因子为Ω时的临界约束比,ζ0,1为强化因子为1时的临界约束比。临界约束比强化系数与强化因子的变化关系如图11b所示。

图11 不同强化因子下支撑临界约束比及其强化系数

由图11可知,随着强化因子的增大,临界约束比及临界约束比强化系数均增大;临界约束比强化系数略小于强化因子,随着强化因子的增大,增加的幅度变小。偏于安全设计时,可用强化因子代替临界约束比强化系数。

3.6 摩擦力

上述有限元分析均未考虑内核芯材与外围约束机制的摩擦力影响,但是,轴向荷载作用下芯材出现横向变形,由于外围套筒的约束作用,在芯材轴向位移下,芯材与外围套筒的摩擦不可避免。

以试件TB-7为例,讨论摩擦系数分别为0、0.1、0.2、0.3下的支撑承载力与位移变化关系,分析结果如图12所示。

由图12可知,没有摩擦时支撑的约束端反力最大,在轴向荷载作用下,内核芯材实现全截面屈服;随着摩擦系数的增大,外围套管分担的轴力愈大,芯材的轴向力沿纵向由加载端到约束端变小,当摩擦系数为0.3时,在2.0%轴向应变下,约束端反力仅为加载段的61%。

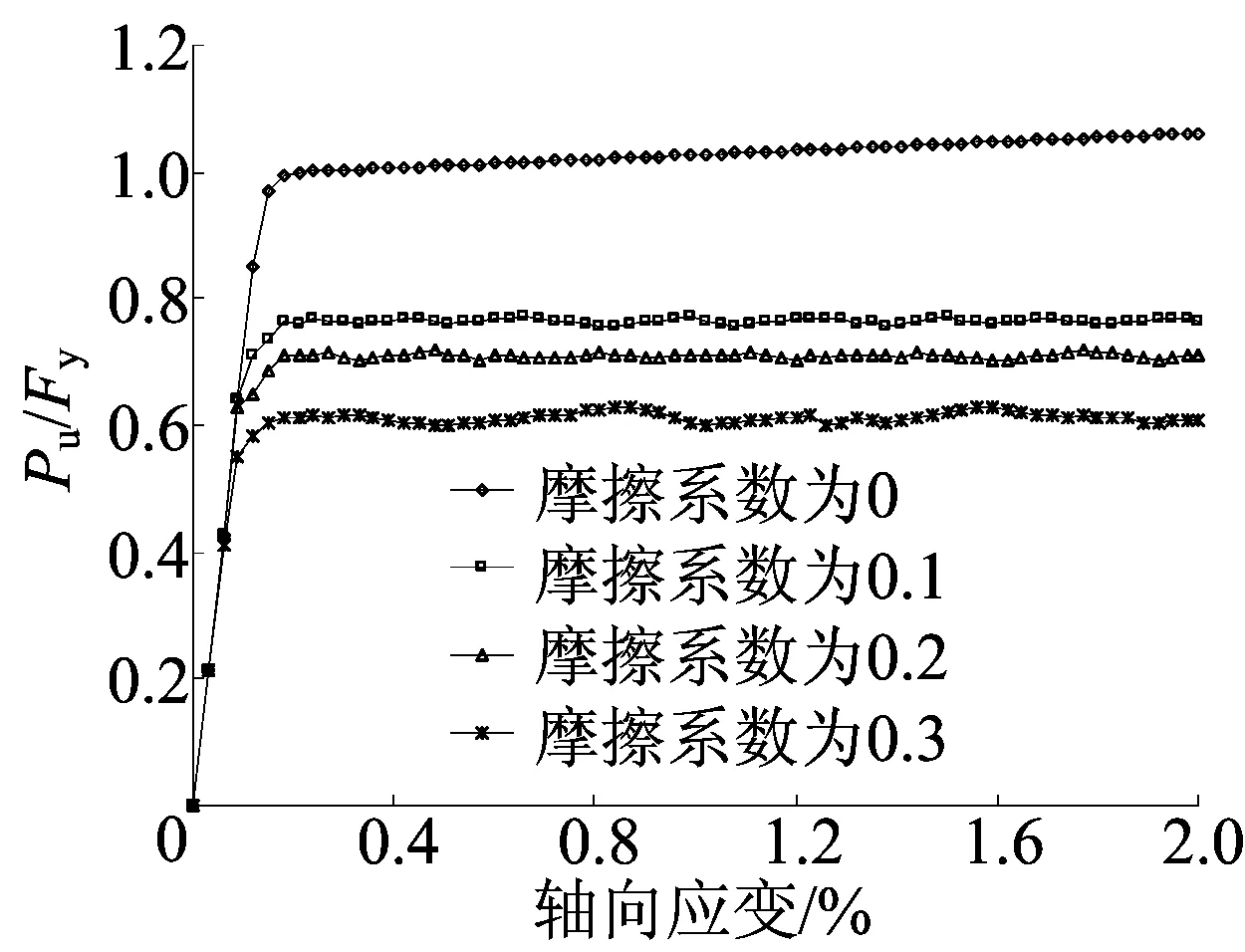
图12 不同摩擦系数时的支撑约束端反力变化曲线

通过上述分析可知,芯材对约束机制的挤压力与芯材屈曲半波的个数是决定摩擦力大小的主要因素。研究表明,间隙大小的改变直接影响挤压力的增减,当间厚比增大时,挤压力随之呈线性提高,所以,在合理的取值范围内尽量取较小的间厚比;芯材的初始缺陷也影响挤压力的变化,初始缺陷愈大,挤压作用愈明显;芯材宽厚比的大小对芯材屈曲时半波的个数及波长起决定作用,宽厚比较大时,屈曲失稳时波长较小,半波的个数变大,使芯材与外围套筒的接触面较多,外套筒承受的摩擦力较大,所以,根据实际情况,优先考虑宽厚比较小的芯材截面。

综上所述,摩擦力的存在使约束端的反力下降,不利于支撑的抗疲劳性能及耗能性能。增大芯材截面厚度、降低间厚比及初始缺陷的影响、合理控制间厚比取值范围均可降低摩擦力影响。

4 结 论

(1) 保证支撑稳定发挥其减震性能的最小约束比为1.51,考虑到其他因素的影响及给予结构一定的安全储备,建议屈曲约束支撑的约束比下限值为2.0,基于经济因素及结构自重考虑,约束比上限值为3.0。

(2) 随着初始缺陷的增大,屈曲约束支撑稳定工作的需求约束刚度亦随之增大;为保证屈曲约束支撑具有稳定的工作性能，建议约束比下限值为2.0。

(3) 宽厚比越大的试件,其承载力下降点所对应的轴向应变值越小;相同轴向应变情况下,宽厚比越大,试件的极限承载力越低,且下降的幅度越大。

(4) 为保证支撑综合性能的稳定发挥,建议间厚比介于0.05～0.1。

(5) 随着应变强化因子的增大,临界约束比及临界约束比强化系数均增大;临界约束比强化系数略小于强化因子,偏于安全设计时,可用强化因子代替临界约束比强化系数。

(6) 摩擦力的存在使约束端的反力下降,不利于支撑的抗疲劳性能及塑性变形;增大芯材截面厚度、合理控制间厚比取值及减小初始缺陷均有利于降低摩擦力的影响。

[1] 齐永胜,顾强,李卫青.中心支撑钢框架顶部薄弱层地震倒塌现象[J].合肥工业大学学报(自然科学版),2015,38(12):1668-1673,1710.

[2] DUSICKA P.Global restraint in ultra-lightweight buckling-restrained braces[J].Journal of Composites for Construction,2013,17(1):139-150.

[3] ZONA A,RAGNI L,DALL A A.Sensitivity-based study of the influence of brace over strength distributions on the seismic response of steel frames with BRBs[J].Engineering Structures,2012,37(3):179-192.

[4] 周云,唐荣,钟根全.防屈曲耗能支撑研究与应用的新进展[J].防灾减灾工程学报,2012,32(8):393-407.

[5] 马宁,吴斌,欧进萍.全钢防屈曲支撑局部稳定性设计[J].工程力学,2013,30(1):134-139.

[6] 郭彦林,姜子钦,王小安,等.双矩管装配式防屈曲支撑约束刚度取值研究[J].工程力学,2015,32(4):22-32.

[7] 周云,尹绕章,张文鑫,等.钢板装配式屈曲约束支撑性能研究[J].建筑结构学报,2014,35(8):37-43.

[8] 吴京,梁仁杰,王春林,等.屈曲约束支撑核心单元的多波屈曲过程研究[J].工程力学,2012,29(8):136-142.

[9] 梁峰.T形截面防压曲支撑静力分析及防压曲支撑布置方案研究[D].北京:北京工业大学,2007.

[10] 赵林.屈曲约束支撑钢框架设计及抗震性能研究[D].西安:西安建筑科技大学,2011.

[11] 刘建彬.防屈曲支撑及防屈曲支撑钢框架设计理论研究[D].北京:清华大学,2005.

[12] 高向宇,张慧,杜海燕,等.防屈曲支撑恢复力的特点及计算模型研究[J].工程力学,2011,28(6):19-28.

(责任编辑 张淑艳)

Study of factors influencing mechanical properties of T-shaped cross-section buckling restrained braces

WANG Yonggui1, XIE Xiaojie2

(1.School of Civil Engineering, Henan Polytechnic University, Jiaozuo 454000, China; 2.Zhengzhou University of Industrial Technology, Zhengzhou 451100, China)

To investigate the effect of structural factors on the mechanical properties of T-shaped cross-section buckling restrained braces(BRB), the stress mechanism of the outsourcing rectangular steel tube concrete BRB was analyzed with the finite element analysis software ANSYS by APDL secondary development. The effect of factors such as restraint stiffness, initial defect, width-to-thickness ratio, gap-to-thickness ratio, core material strain hardening and friction on BRB was studied. The results showed that the impact of initial defect of core material decreased with the increase of restraint stiffness, and the minimum restraint ratio to maintain the stable state of BRB was 2.0. The bearing capacity of BRB did not change significantly when the gap-to-thickness ratio was between 0.05 to 0.1. The influence of friction was reduced with the increase of cross-sectional thickness of core material, the reasonable control of gap-to-thickness ratio and the decrease of initial defect of core material.

buckling restrained braces(BRB); finite element; mechanical property; influencing factor

2015-04-16；

2016-02-23

河南省科学技术重点资助项目(14A560001);河南理工大学博士基金资助项目(B2015-69)

王永贵(1977-),男,河南确山人,博士,河南理工大学副教授,硕士生导师.

10.3969/j.issn.1003-5060.2016.09.018

TU352.11

A

1003-5060(2016)09-1241-07