利用快速傅里叶变换的双层搜索目标跟踪算法

张 浪,侯志强,余旺盛,许婉君

(空军工程大学信息与导航学院,陕西西安 710077)

利用快速傅里叶变换的双层搜索目标跟踪算法

张 浪,侯志强,余旺盛,许婉君

(空军工程大学信息与导航学院,陕西西安 710077)

针对视觉跟踪中目标表观变化、尺度及旋转变化问题,提出了利用快速傅里叶变换的双层搜索目标跟踪算法.算法在直角坐标系和对数极坐标系分别构建目标核岭回归模型并进行目标双层搜索,同时利用快速傅里叶变换将时域运算转换到频域运算提高跟踪效率.首先在直角坐标系中建立目标核岭回归模型并构建循环结构矩阵进行穷搜索得到目标中心位置;然后以目标中心位置为原点将跟踪区域变换到对数极坐标系再次建立目标核岭回归模型,并穷搜索得到目标在对数极坐标系的平移量;最后依据搜索结果确定目标状态并进行模型更新.实验结果表明,这种算法不仅对表观变化、尺度及旋转变化具有较强的鲁棒性,而且跟踪实时性较好.

视觉跟踪;双层搜索;对数极坐标;快速傅里叶变换

随着计算机视觉和多媒体技术的迅速发展,目标跟踪问题受到越来越多学者的关注[1-3].目标运动过程中表观、尺度及旋转角度不断变化是跟踪失败的重要原因,因此如何构建鲁棒的表观模型及实现目标的快速搜索是当前研究的热点.Mean Shift算法[4]利用颜色直方图特征构建目标模型,但容易匹配到具有相似颜色直方图特征的背景中去;文献[5]提出融合多种特征进行目标跟踪,增强了对背景变化的适应性;文献[6]提出利用局部分块构建目标模型,能有效地解决遮挡问题;文献[7]增强了目标分块的自适应能力,能较好地适应目标形变问题;基于循环结构的检测跟踪法[8-9]提出利用循环结构矩阵建立目标回归跟踪模型,但算法对于复杂背景干扰及遮挡变化比较敏感.近年来,基于压缩感知和稀疏子空间理论为构建目标模型提供了新思路.文献[10]通过目标的正负样本集建立目标的稀疏相似图,然后利用该相似图搜索与目标最相似的候选目标.文献[11]将目标模型映射到一组由特征基张成的子空间,并利用稀疏理论对目标进行压缩感知描述.

笔者提出在直角坐标系和对数极坐标系分别构建目标核岭回归模型,并利用快速傅里叶变换进行双层搜索.利用目标表观信息在直角坐标系构建表观模型精确搜索目标位置,进而利用对数极坐标的尺度旋转不变性确定目标的尺度和旋转变化量.同时,算法通过构造循环结构矩阵将时域运算变换到频域运算以提高跟踪效率.实验结果表明,该算法不仅能较好地适应表观、尺度及旋转变化,而且跟踪实时性较好.

1　相关理论介绍

笔者采用在直角坐标系和对数极坐标系分别构建目标核岭回归模型,并利用快速傅里叶变换进行双层搜索.先介绍核岭回归及对数极坐标理论.

1.1基于快速傅里叶变换的核岭回归

线性回归是利用数理统计中的回归分析,输出变量是输入变量的线性组合[8]:

其中,wTx是变量之间的内积;ζ表示预测值与真实值的偏差,一般服从标准正态分布,即ζ∝N(0,δ2).

通过构造代价函数并求解得到岭回归解:

其中,λ为正则化参数.

利用核技巧,可将线性回归转化为非线性回归.将内积x xT用核矩阵K代替,得到核岭回归的解:

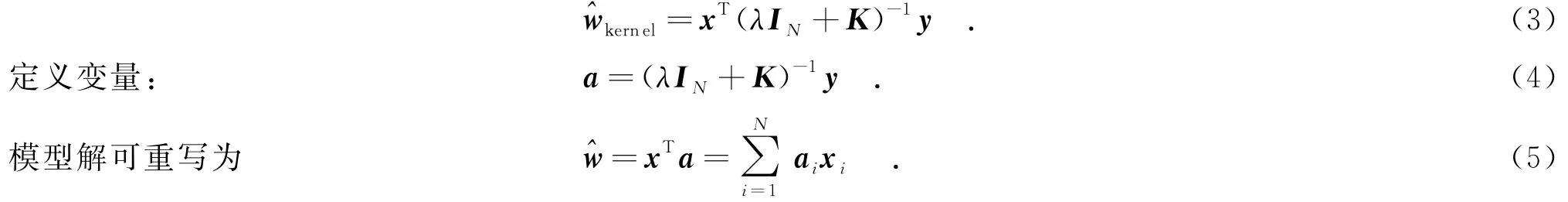
对于新的图像样本x′,根据模型可以预测该样本属于目标的响应:

类似一维序列构造循环结构矩阵原理,通过构造循环结构矩阵可将式(4)从时域变换到频域求解[8]:

需要注意的是,二维矩阵循环沿水平和垂直两个方向进行[9],其示意图如图1所示.

图1　构造循环结构示意图

由于一幅图像对应一个像素矩阵,则对一个图像块x,通过对原始图像进行水平及垂直方向循环移位,可得到一系列训练样本,从而构造循环结构矩阵并建立目标模型.笔者取图像块x为目标区域的M倍,定义y为与x等大小且满足高斯分布的函数,y的每个取值对应不同训练样本的响应值,通过构造循环结构建立目标训练样本与对应响应值的映射关系,并利用快速傅里叶变换将模型构建从时域运算转换到频域运算.需注意,循环结构矩阵由原始图像矩阵循环移位得到,其频域运算可快速求得所有训练样本与响应值映射关系.在下一帧图像块x′中,利用目标模型在频域进行模型学习,可快速实现对所有位置遍历穷搜索.

1.2对数极坐标变换(LBP)

一幅图像可以用直角坐标系(x,y)描述,也可以用对数极坐标(ξ,ψ)描述,它们的关系如下[12]:

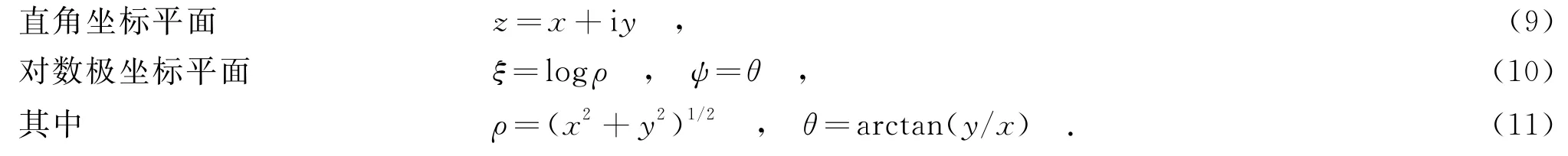
图像的对数极坐标表示具有重要性质,在直角坐标系下的尺度和旋转变化可转化为对数极坐标系下沿半径和角度轴的平移变化.假设图像在直角坐标系下以目标为中心变为原来的k倍、旋转φ弧度时,则

可以看出,在对数极坐标系中,图像的尺度变化表现为沿极半径平移,旋转变化表现为沿极角平移.

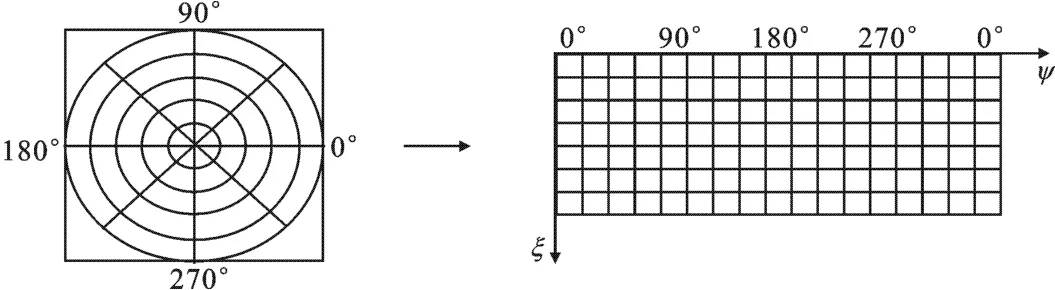
图2　对数极坐标变换原理图

2　跟踪算法

算法实现分两步:首先,在直角坐标系中,在包含目标的跟踪区域建立目标核岭回归模型,构造循环结构矩阵进行穷搜索得到目标中心位置;然后,在对数极坐标系中,将以目标中心为原点的跟踪区域变换到对数极坐标再次建立核岭回归模型,并利用对数极坐标系的尺度旋转不变性估计目标的尺度和旋转变化.

2.1直角坐标系目标穷搜索

在直角坐标系中,笔者采用基于快速傅里叶变换的目标穷搜索方法.由于利用目标表观信息构建目标模型,算法对表观变化、背景干扰等适应性较好.目标模型通过在第一帧图像中手动标注获得训练样本,然后利用上述介绍的核岭回归理论建立模型.目标的直角坐标系模型表示为

其中,(x,y)表示手动标注的目标中心位置.

在对目标进行搜索时,该算法将搜索区域设定为以上帧跟踪结果为中心的4倍目标尺寸的区域,通过构建循环结构矩阵并将时域运算转换到频域运算进行快速穷搜索,得到目标的中心位置(x′,y′).

2.2对数极坐标系目标穷搜索

对数极坐标具有尺度旋转不变性,但很少有好的模型能利用该性质来估计目标的尺度和旋转变化.笔者将基于快速傅里叶变换的穷搜索方法引入对数极坐标域,通过搜索目标在对数极坐标系的平移量来精确估计尺度和旋转变化.以目标中心位置为原点将跟踪区域变换到对数极坐标并建立目标对数极坐标系模型:

其中,(i,j)表示目标对数极坐标区域中心位置.

通过对数极坐标穷搜索得到目标在对数极坐标系的平移(m,n),则其在直角坐标系的尺度和角度为

其中,Wt和θt分别为目标在t帧的尺度和角度,k1和k2分别为极半径与极角的映射因子.

2.3模型更新

为适应目标变化及减少背景的干扰,采用线性加权机制来对目标模型进行更新.算法设置两个模型更新因子α和β分别对直角坐标系模型wcar和对数极坐标系模型wlog进行实时更新:

其中,wt表示第t帧的直角坐标系模型wcar或对数极坐标系模型wlog,υ为对应的模型更新因子.

2.4算法流程

基于快速傅里叶变换的双层搜索目标跟踪算法如下.

输入:图像Ik,初始目标位置O0,初始跟踪框Obb0.

输出:当前帧目标状态(Ok,Obbk).

如果k=1:

第1步 根据初始条件确定目标区域,并变换到对数极坐标系.

第2步 在直角坐标系和对数极坐标系分别建立目标核岭回归模型wcar和wlog.

如果k＞1:

第1步 在直角坐标系中,根据输入条件确定搜索区域,构造循环结构矩阵穷搜索得目标中心位置Ok.

第2步 将以Ok为中心的目标区域变换到对数极坐标系,并利用模型wlog搜索目标的平移量(m,n).

第3步 根据上述搜索结果确定目标状态(Ok,Obbk),并进行模型更新.

笔者提出算法的流程图如图3所示.

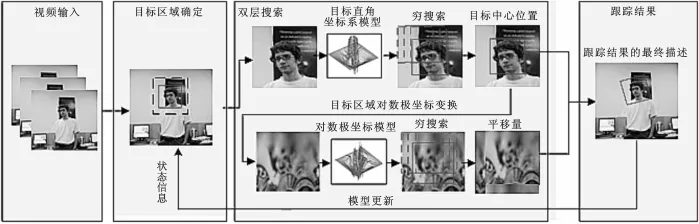
图3　算法流程图

3　实验结果与分析

为验证上述跟踪算法的有效性,进行了大量的实验仿真.实验中设置直角坐标系目标穷搜索范围为目标大小的4倍,对数极坐标系穷搜索范围为目标大小的2倍,核岭回归模型正则化参数λ=0.01,高斯核方差δ=0.1,直角坐标系和对数极坐标系的模型更新因子为α(0.05≤α≤0.15)和β(0.05≤β≤0.15).α和β取值区间是经过大量实验得到的,对不同视频需人为设定最佳值.

为说明该算法在处理目标表观变化、尺度及旋转变化等的优势,有针对性地选取了6组具有挑战性的测试视频和4种对比算法:除Sylvester-2008视频、Cliffbar视频及目标真实位置来自文献[10]外,其余视频及真实位置均来自文献[3];4种对比算法分别为BHT[7],CSK[8],CT[11]和DSSM[10].为保证对比试验的公平性,CSK算法和CT算法的跟踪结果直接使用文献[3]的公开结果,其余算法均为多次实验取最优结果.所有实验都在联想CPU-E5300,2.60 GHz,3.25 GB内存的台式机进行,算法通过MATLAB 2009a实现.

3.1定性对比

3.1.1Boy序列

“Boy序列”的跟踪难点是快速运动、尺度和旋转变化.如图4(a)所示,当目标快速运动时,BHT算法出现跟踪丢失,CT算法出现一定程度偏差;与CSK算法相比,虽都进行了穷搜索,笔者提出的算法通过双层搜索具有更好的鲁棒性,而CSK算法跟踪丢失,如第602帧所示;DSSM算法和笔者提出的算法均能较好地跟踪目标.

3.1.2Dog1序列

“Dog1序列”的跟踪难点是目标表观变化和明显的尺度变化.如图4(b)所示,当目标尺度发生明显的变化时,BHT算法和CSK算法由于不能适应尺度变化而出现一定程度的偏差;DSSM算法虽然也具有尺度自适应能力,但也未能较好地适应尺度的明显变化,如第1 001帧所示(图左上角为当前帧数);笔者提出的算法通过建立核岭回归模型进行双层穷搜索,不仅能较准确地搜索目标位置,而且能较好地适应目标尺度的变化.

3.1.3David2序列

“David2序列”的跟踪难点是目标表观变化、背景干扰及平面内的旋转变化.如图4(c)所示,由于背景的干扰,CT算法未能正确地区分目标和背景而导致跟踪目标丢失;当目标进行连续的转动时,BHT算法也丢失跟踪目标;CSK算法、DSSM算法及笔者提出的跟踪算法均能成功地跟踪目标,但是笔者提出的算法通过双层穷搜索能更好地适应目标的变化,跟踪精度更高,如第485帧所示.

3.1.4Cliffbar序列

“Cliffbar序列”的跟踪难点是目标表观变化、复杂背景干扰及尺度和旋转变化.如图4(d)所示,由于目标表观不断变化及背景干扰,BHT算法、CT算法和CSK算法均丢失跟踪目标,如第342帧所示;笔者提出的算法和DSSM算法均能成功地跟踪目标,但后段序列目标尺度和旋转的快速变化,使笔者提出的算法亦出现一定误差.

3.1.5Sylvester-2008b序列

“Sylvester-2008b序列”的跟踪难点是由平面外旋转导致的表观变化及光照变化.如图4(e)所示,当目标在灯光下运动时,由于存在平面外的转动,目标表观姿态改变较大,CT算法跟踪丢失,BHT算法、CSK算法及DSSM算法均出现一定程度的偏差,如第343帧所示;笔者提出的算法相对能更好地跟踪目标.

3.1.6Singer序列

“Singer序列”的跟踪难点是存在尺度变化及复杂背景干扰.如图4(f)所示,由于复杂的背景干扰,BHT算法和CT算法均出现偏差;当目标尺度不断缩小时,CSK算法虽能成功地跟踪目标,但不能适应目标的尺度变化;DSSM算法和笔者提出的算法均能较好地跟踪目标,但笔者提出的算法对目标的变化适应性更好.

图4　跟踪算法性能的定性比较

3.2定量分析

为衡量跟踪算法的跟踪性能,笔者采用中心位置误差、跟踪成功率和平均每帧运行时间来对笔者提出的算法和对比算法进行对比分析.中心位置误差和跟踪成功率衡量跟踪精度.误差值越小,跟踪精度越好;成功率值越大,跟踪精度亦越好.平均每帧运行时间衡量跟踪效率,时间值越小,跟踪效率越高.

3.2.1中心位置误差

图5所示为中心位置误差对比曲线.BHT算法在Sylvester-2008b序列跟踪误差相对较小,CT算法在David2序列和Cliffbar等序列跟踪误差较大.除了Boy序列和Cliffbar序列,CSK算法在其他序列跟踪精度较高,这是由于算法通过构建循环结构矩阵进行目标穷搜索,能在一定程度适应目标表观变化.DSSM算法通过正负样本构建目标模型,增强了算法对表观变化及背景干扰等的适应能力,除了Dog1序列,DSSM算法在其他序列跟踪结果均较理想.笔者提出的算法分别在直角坐标系和对数极坐标系构建目标核岭回归模型,并进行双层搜索,增强了算法对目标表观变化、尺度和旋转变化等的适应能力,因此在所有序列均取得较小的中心位置误差.

图5　中心位置误差比较

表1中每种算法第1列所示为目标中心位置平均误差值(CLE),其中粗正体表示最优算法,粗斜体表示次优算法.可以看出,笔者提出的算法除在Boy序列和Cliffbar序列取得次优跟踪结果外,在其他视频序列均取得最优跟踪结果,具有最优的平均跟踪误差值.

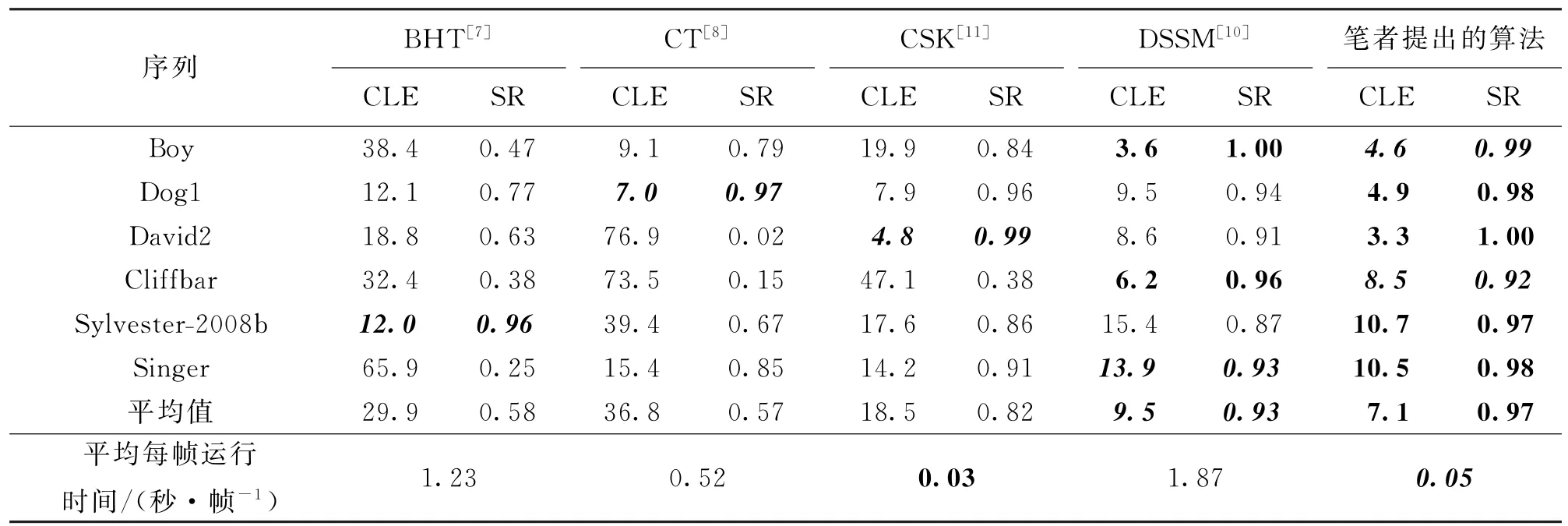
表1　中心位置误差和跟踪成功率比较

3.2.2跟踪成功率

表1中每种算法第2列所示为跟踪成功率(SR).笔者提出的算法在所有测试视频序列中取得4组最优结果和2组次优结果,在平均跟踪成功率上取得最优结果.DSSM算法在Boy序列和Cliffbar序列取得最优结果,在Singer序列取得次优结果,在平均跟踪成功率上取得次优结果.

表1中最后一行是算法平均每帧运行时间.笔者提出的算法和CSK算法都具有较高的跟踪效率,主要是这两种算法均利用快速傅里叶变换将时域运算转换到频域运算,虽然笔者提出的算法在直角坐标系与对数极坐标系分别构建目标模型进行双层穷搜索增加了算法复杂度,但跟踪效率较一般算法仍具有较大优势.

3.3讨 论

实验发现,笔者提出的算法相比其他算法在跟踪精度和跟踪效率上具有一定优势,但是在极坐标系的穷搜索模型是以在直角坐标系的目标定位为前提的.当目标定位误差较大时,在极坐标系穷搜索得到的目标平移量将不准确,由此估计目标尺度和旋转变化量将存在一定误差,如图4中Cliffbar序列第342帧和Sylvester-2008b序列的343帧所示,这是笔者提出的跟踪算法的不足.

4　总 结

笔者提出了一种利用快速傅里叶变换的双层穷搜索目标跟踪算法,在直角坐标系和对数极坐标系分别构建目标核岭回归模型,并利用快速傅里叶变换进行双层穷搜索.首先,在直角坐标系构建目标表观模型并穷搜索得到目标中心位置,然后在对数极坐标系搜索目标平移量,进而利用对数极坐标的尺度旋转不变性确定目标的尺度和旋转变化量,同时,算法通过构造循环结构矩阵将时域运算变换到频域运算,有效地提高了跟踪效率.实验结果表明,笔者提出的算法能较好地处理目标表观变化、尺度及旋转变化等问题,取得较好的跟踪精度和跟踪效率.需要指出的是,笔者提出算法的跟踪精度对直角坐标系目标位置定位依赖度较大,当目标位置定位误差较大时,对目标尺度和旋转估计误差较大,从而在模型更新时会引入较多的背景信息,这是笔者提出算法的不足.下一步工作将考虑通过跟踪检测判断机制来避免上述问题发生,进一步提高算法的有效性和鲁棒性.

[1]SMEULDERS A W,CHU D M,CUCCHIARA R,et al.Visual Tracking:an Experimental Survey[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2014,36(7):1442-1468.

[2]侯志强,韩崇昭.视觉跟踪技术综述[J].自动化学报,2006,32(4):603-617. HOU Zhiqiang,HAN Chongzhao.A Survey of Visual Tracking[J].Acta Automatica sinica,2006,32(4):603-617.

[3]WU Y,LIM J,YANG M H.Online Object Tracking:a Benchmark[C]//International Conference on Computer Vision and Pattern Recognition.Washington:IEEE Computer Society,2013:2411-2418.

[4]COLLINS R T.Mean-shift Blob Tracking through Scale Space[C]//Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition.Los Alamitos:IEEE Computer Society,2003:234-240.

[5]李远征,卢朝阳,李静.一种基于多特征融合的视频目标跟踪方法[J].西安电子科技大学学报,2012,39(4):1-6. LI Yuanzheng,LU Chaoyang,LI Jing.Robust Video Object Tracking Algorithm based on Multi-feature Fusion[J]. Journal of Xidian University,2012,39(4):1-6.

[6]ADAM A,RIVLIN E,SHIMSHONI I.Robust Fragments-based Tracking Using the Integral Histogram[C]//Proceedings of IEEE International Conference on Computer Vision and Pattern Recognition.Los Alamitos:IEEE Computer Society,2006: 798-805.

[7]NEJHUM S M S,HO J,YANG M H.Online Visual Tracking with Histograms and Articulating Blocks[J].Computer Vision and Image Understanding,2010,114(8):901-914.

[8]HENRIQUES J F,CASEIRO R,MARTINS P,et al.Exploiting the Circulant Structure of Tracking-by-detection With Kernels[C]//Proceedings of European Conference on Computer Vision.Heidelberg:Springer Verlag,2012:702-715.

[9]HENRIQUES J F,CASEIRO R,MARTINS P,et al.High-speed Tracking with Kernelized Correlation Filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2015,37(3):583-596.

[10]ZHUANG B H,LU H C,XIAO Z Y,et al.Visual Tracking via Discriminative Sparse Similarity Map[J].IEEE Transactions on Image Processing,2014,23(4):1872-1881.

[11]ZHANG K,ZHANG L,YANG M H.Real-time Compressive Tracking[C]//12th European Conference on Computer Vision.Heidelberg:Springer-Verlag,2012:864-877.

[12]METTA G,GASTERATOS A,SANDINI G.Learning to Track Colored Objects with Log-polar Vision[J].Mechatronics,2004,14(9):989-1006.

(编辑:郭 华)

Two-level searching tracking algorithm based on fast Fourier transform

ZH ANG Lang,HOU Zhiqiang,YU Wangsheng,XU Wanjun
(Information and Navigation College,Air Force Engineering Univ.,Xi’an 710077,China)

In order to solve the problems of appearance change,scale and rotation change in the visual tracking,a two-level searching tracking algorithm based on Fast Fourier Transform(FFT)is proposed.It achieves two-level searching by establishing the object’s kernel ridge regression model in the Cartesian coordinates and log-polar coordinates,respectively,and the efficiency can be improved by transforming the operation into the frequency domain based on FFT.First,the kernel ridge regression model is constructed in the Cartesian coordinate and the object’s center position is obtained by the exhaustive search method based on the circular structure matrix.Then,it transforms the object area to the log-polar coordinates and searches the shift using the kernel ridge regression model in the log-polar coordinates.Finally,the object’s state is calculated according to the searching results and the object’s model is updated.Experimental results indicate that the proposed algorithm not only can obtain a distinct improvement in coping with the appearance change,scale and rotation change,but also have a high tracking efficiency.

visual tracking;two-level searching;log-polar coordinate;fast Fourier transform

TP391

A

1001-2400(2016)05-0153-07

10.3969/j.issn.1001-2400.2016.05.027

2015-07-21 网络出版时间:2015-12-10

国家自然科学基金资助项目(61175029,61473309);陕西省自然科学基金资助项目(2011JM8015,2015JM6269)

张 浪(1990-),男,空军工程大学硕士研究生,E-mail:zhanglangwy@126.com.

网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.054.html