多核处理器中并行自适应索引算法优化

袁 通,刘志镜,刘 慧

(西安电子科技大学计算机学院,陕西西安 710071)

多核处理器中并行自适应索引算法优化

袁 通,刘志镜,刘 慧

(西安电子科技大学计算机学院,陕西西安 710071)

针对现有的多核并行自适应索引算法不能高效地利用多核处理器的并行资源,且不能较好处理顺序查询的问题,提出了一种改进的多核并行自适应索引算法.该算法在优化现有Refined Partition Merge算法的基础上,将加锁并行方法与Refined Partition Merge算法相结合,在索引中数据块较少时,使用优化的Refined Partition Merge算法,降低线程之间冲突的概率,减少线程等待时间,提高线程利用率.当索引中数据块较多时,使用加锁并行方法,充分利用了多核处理器的并行资源.除此之外,还提出了一种提升自适应索引鲁棒性的优化方法,使多核并行自适应索引算法能够适应两种常用查询样式.实验结果表明,该算法使多核并行自适应索引在查询时间上明显降低,使查询速度提升25.7%～33.2%,并且能够适应多种常用查询样式.

自适应索引;多核处理器;Database Cracking算法;数据库系统

随着海量数据时代的到来,系统数据库的规模越来越大,如何快速检索数据成为数据库领域一个重要的课题.索引技术可以大幅提高检索数据的效率,常用的索引包括:平衡二叉树、B+树索引、哈希索引[1]、ART树索引[2]等.但这些索引技术有以下缺点:索引需要在查询之前创建完成,这个过程消耗大量的时间和空间;索引需要涵盖表中的所有行,即使其中的一些行极少的被查询.

自适应索引技术[3]自提出以来,受到了广泛的关注[4-8],较好地解决了传统索引的缺点.与传统的索引不同,自适应索引的核心思想是根据查询条件动态地、自适应地建立和优化索引结构,索引的建立是查询任务的一个部分.该技术对表中经常查询到的行会建立更好的索引,对那些没有被查询到的行不会建立索引.

当今的中央处理器(Central Processing Unit,CPU)拥有更多的核心,每个核心拥有更多的线程.IBM推出了新一代的POWER 8处理器,支持12核心96线程,共享96 MB的三级缓存,这说明多核CPU具有广阔的应用前景.但目前对于多核并行自适应索引技术的研究还不是很多,仅有的一些研究成果[4-5]也存在一定的不足.文献[4]提出用加锁的方式避免线程之间的冲突,实现并行索引,然而频繁的加锁和解锁操作耗费了大量的时间.文献[5]提出了Partition Merge算法,在该算法中所有线程每次共同处理一个查询任务.该算法虽然避免了频繁的加锁解锁操作,但当所有线程共同处理一个较小的查询任务时,不能高效利用处理器并行资源,容易造成资源浪费.

针对上述问题,笔者提出了一种改进的多核并行自适应索引算法,该算法在优化传统并行自适应索引的基础上,将加锁并行方法与优化的Refined Partition Merge算法相结合,充分利用了多核处理器的并行资源,取得良好的效果.除此之外,文中提出的优化方法使自适应索引能够较好地适应常用的两种查询样式(随机查询和顺序查询),提升了自适应索引的鲁棒性.

图1　Database Cracking算法流程示例

1　相关工作

Database Cracking算法[3]作为自适应索引的核心被广泛采用.Database Cracking首先将表中需要建立索引的数据复制到一个连续的空间作为索引的物理结构,其次根据每次查询条件对索引进行重新划分,重新划分的过程类似快速排序,查询的边界点类似快速排序中的支点.最后还需要一个二叉树来保存划分信息(该二叉树称为Cracker index),树节点〈X,Y〉表示在索引中从位置Y开始的所有数据都大于X.图1给出了Database Cracking方法的基本流程.当进行查询(10,30)时,索引被划分为了3块:小于10的部分、(10,30)的部分、大于30的部分,其中(10,30)的部分作为查询结果返回.节点〈10,2〉和〈30,7〉也同时保存在树中.当进行第2次查询(25,40)时,(10,30)的块再次被分成(10,25)和(25,30)两块,大于30的部分也被分成(30,40)和大于40的两块,其中,(25,30)和(30,40)两块作为查询结果返回.同时,节点〈25,5〉和〈40,10〉也保存在树结构中以便后续查询使用.Database Cracking算法的优势是:每次查询只需处理索引中包含查询边界的两个数据块,并不需要处理整个查询范围之间的数据块.所以当查询次数越多,索引被划分的越细,索引中每块数据越小,则索引被建立的越好,该范围内后续查询所用的时间越短.

目前针对Database Cracking算法的研究主要在以下3个方面:提高算法收敛速度、提高算法鲁棒性以及利用并行提高算法效果.Hybrid Cracking算法[6]结合了Adaptive Merging算法[7]和标准Database Cracking算法各自的优势,在保证较低初始化花销的同时,提高了算法的收敛速度.Buffered-swapping算法[9]利用两个堆结构存储需要交换元素,提升了算法的收敛速度.文献[10]针对顺序查询样式引出的问题,提出了DDR,DDC以及MDD1R等算法,以提高算法鲁棒性,其中DDR算法取得了较好的效果.文献[4]研究了并行Database Cracking算法,通过加锁的方式避免线程间的冲突,实现算法并行化.文献[5]提出了Refined Partition Merge算法,在该算法中所有线程每次共同处理一个查询任务.

2　多核并行自适应索引优化

2.1实验环境

文中的实验环境基于新型英特尔Sandy Bridge架构的Xeon 8核处理器(E5-2670 2.6 GHz),每核包含2个线程.具体配置为:核数为8,线程数为16,一级缓存大小为每核32 KB;二级缓存大小为每核256 KB;三级缓存大小为共享20 MB;内存大小为4×8 GB DDR3内存(1 600 Hz);Cache line大小为64 B.

实验采用与相关论文相同的数据集.该数据集有108条数据,每条数据是大小为4 B的整型数,108条数据在[0,108)范围内随机产生且均匀分布.

采用的查询格式为:SELECT SUM(R.A)FROM R WHERE Ql＜R.A＜Qh.

文中讨论两种查询样式:随机查询和顺序查询,这两种查询均为相关论文所讨论的主要查询方式.图2给出随机查询样式和顺序查询样式,其中黑圈表示查询下限Ql,白圈表示查询上限Qh,两种查询的选择率均为1%.

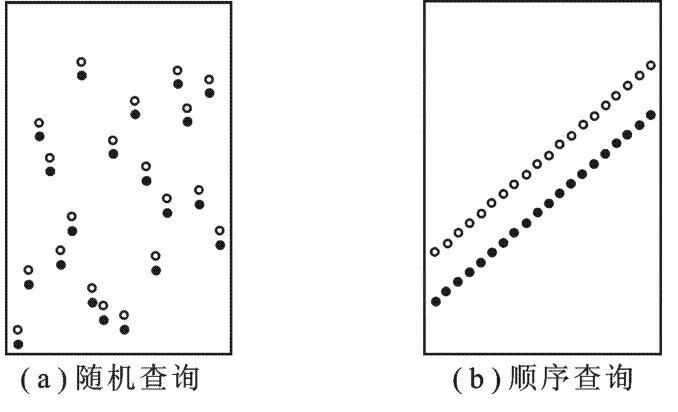
图2　文中所用的两种查询样式

2.2Refined Partition Merge算法的优化

文献[5]提出了Refined Partition Merge算法,所有线程共同处理一条查询任务.假设索引结构中有S个元素,线程数量为T,现将索引结构划分为T块.前T-1块中,每块含有S/T个元素,且由两个不相邻的子块组成,每个子块有S/(2T)个元素,每个子块的位置对称于索引中心位置的两侧;第T块含有剩余元素(考虑元素不能等分的情况),其元素连续的分布于索引中心位置两侧,如图3所示.在划分阶段,每一个线程负责一块数据,并行地执行标准Database Cracking算法;在合并阶段,将位置错误的元素进行位置交换,最终得到正确的Database Cracking结果.在该算法中每一个线程负责两个不相连的数据子块,这样避免了Merge阶段大量元素的交换,提高了合并阶段的效率.

图3　Refined Partition Merge算法示例

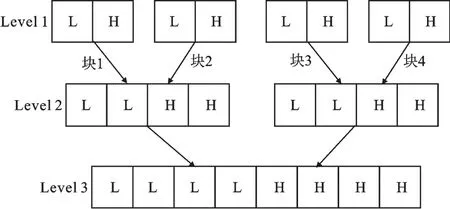
图4　并行合并示例

在Refined Partition Merge算法中,合并阶段是由一个线程独立完成的,没有充分利用处理器的并行资源.文中的优化是对合并阶段进行并行化处理,利用多路并行归并的思想,分层将块中位置错误的元素进行交换.在图4中,L代表小于支点的数据,H代表大于支点的数据.块1和块2分别经过Database Craking处理后,块内相对有序,块间无序.如图4所示,一个线程将块1和块2中位置错误的元素进行交换后,形成一个新块,等待进行下一层的交换.每层之中的交换可以多线程并行处理,经过多层交换以后最终得到元素位置正确的索引.图4举例说明并行合并过程,其中每层的交换可以并行处理,经过两层交换后得到最终正确的结果.

2.3改进的多核并行自适应索引算法

在加锁并行方法中,每一个线程每次负责一条查询任务,索引中的每一个数据块有一个读写锁,整个Cracker index(即保存划分信息的二叉树)有一个读写锁,这些读写锁避免了线程之间的冲突.当一个线程对某一数据块处理时,会对该数据块加锁.这时对数据块进行任何操作的其他线程都会被阻塞,直至该数据块被解锁.算法对Cracker index允许多线程并行读操作,但不允许并行写操作.

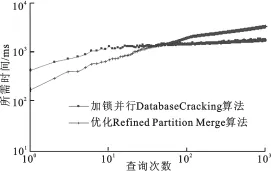
图5　两种并行算法性能比较

以上两种算法都有各自的优缺点,图5给出了两种算法在8线程环境下进行1次至1 000次随机查询时分别所需的时间.从图5可以看出,当查询次数较少时优化Refined Partition Merge算法效果较好,当查询次数较多时加锁并行Database Cracking算法效果较好.这是因为:当查询次数较少,索引中数据块较少时,特别是前几次查询时,加锁并行Database Cracking算法中线程之间冲突的概率增大,算法性能降低.以第1次查询为例说明:当进行第1条查询任务时,整个索引只是一整块数据,没有任何划分,此时只有一个线程可以工作,其余线程需要等待.这耗费了大量时间,浪费了并行资源,特别是当索引数据特别大时.此时优化Refined Partition Merge算法不会浪费其他线程的计算资源,所以取得较好的效果.当查询次数较多,索引中数据块较多时,加锁并行Database Cracking算法中线程之间冲突的概率较小,线程等待锁的平均时间大大降低,所以此算法效率较高.然而此时,优化Refined Partition Merge算法依然让所有线程并行处理一个数据块,即使该数据块很小,这样大部分时间花费到线程建立、数据分配等操作上,所以当查询次数增加,优化Refined Partition Merge算法性能降低.文中提出了一种改进的多核并行自适应索引方法.该方法将优化Refined Partition Merge算法和加锁并行Database Cracking算法相结合,在前几次查询时或者处理索引中较大的数据块时,使用优化的Refined Partition Merge算法,降低线程之间冲突的概率,减少线程等待时间,提高线程利用率.随着查询次数和索引中数据块的增加,之后的查询则使用加锁解锁方法,避免了Refined Partition Merge在处理索引中小数据块时的不足.在此提出的优化方法适用于同一数据集上的多次范围查询.当查询次数较少时,利用2.2节提出算法即可.

2.4提升算法鲁棒性的优化

鲁棒性是自适应索引算法一个关键的因素,强壮的鲁棒性可以使文中算法适应多种样式的查询.标准的Database Cracking算法(单线程)和加锁并行Database Cracking算法(多线程)都不能很好的处理顺序查询.图6给出了加锁并行Database Cracking算法处理随机查询和顺序查询的实验结果,从图中可以看出,加锁并行Database Cracking算法能够很好处理随机查询,但对顺序查询处理效果不佳.主要因为:加锁并行Database Cracking算法仅根据每个查询的边界对数据块进行划分.在顺序查询中,每次划分将一个数据块分为两个大小相差很大的数据块,其中一个数据块很大,另一个却很小.这使后续的查询需要遍历较大的数据块,增加了开销.

图6　两种查询样式的性能比较

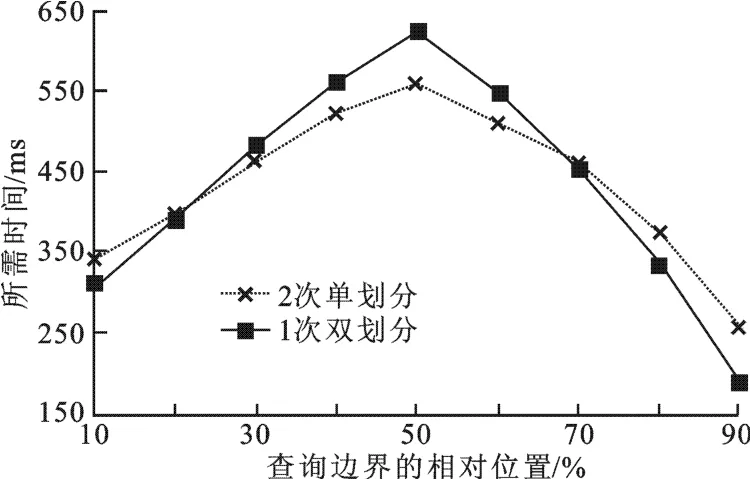
图7　划分支点位置对性能的影响

针对上述问题,在DDR算法[10]的基础上,提出了一种优化方法.思路是:在改进的多核并行自适应索引方法中,无论优化Refined Partition Merge算法还是加锁并行Database Cracking算法,在进行一次由查询驱动的划分后,都额外进行一次随机划分,并将产生的两个新节点均加入Cracker index之中.

3　实验结果及分析

3.1优化Refined Partition Merge算法的实验结果

为了验证对原Refined Partition Merge算法的优化效果,将优化的算法(2.2节)与原算法在不同线程数下进行了比较.实验采用2.1节所述的数据集和随机查询样式,实验结果如图8所示.从图8可以看出:优化后的算法与原算法相比,性能有所提高;当线程数为1时,两个算法所需时间一样;当线程数从8增加到16时,算法性能提升不明显.这是因为,首先,采用了并行合并算法,减少了合并阶段的时间消耗,算法性能得到了提升;其次,当线程数为1时,不需要进行合并操作,所以两个算法所需的时间相同;最后,由于实验机器为8核16线程,总线资源和缓存资源按核分配.所以当线程数量为16时,核内线程之间会竞争总线、缓存等资源,所以,当线程数从8增加到16时,算法性能提升不明显.

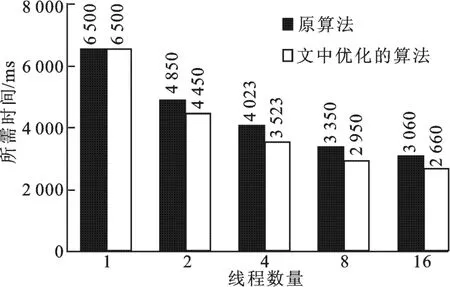
图8　优化Refined Partition Merge算法的实验结果

图9　改进的多核并行自适应索引算法实验结果

3.2改进的多核并行自适应索引算法的实验结果

图9给出了改进的多核并行自适应索引算法(2.3节)与其他两种常用的并行自适应索引算法在不同线程数量下的对比结果.实验采用2.1节所述的数据集和随机查询样式,文中算法在前5%次查询(即前50次)使用优化的Refined Partition Merge算法,剩余查询使用加锁并行Database Cracking算法.由图9可以看出,文中算法与原有的算法相比,性能有了明显的提高.这是由于在前50次查询时使用优化的Refined Partition Merge算法,提高了算法处理大数据块时的效率;在剩余查询时使用加锁并行Database Cracking算法时,由于此时索引中数据块较多,线程之间冲突的概率减小,且与优化的Refined Partition Merge算法大幅减少了线程创建、数据分配等操作的开销.当线程数量为16时,核内线程之间会竞争总线、缓存等资源,所以当线程数从8增加到16时,算法性能提升不明显.

3.3算法鲁棒性优化的实验结果

图10给出了算法鲁棒性优化(2.4节)的实验结果,实验采用2.1节所述的数据集和顺序查询样式.图10进一步验证了2.4节中加锁并行Database Cracking算法不能很好的处理顺序查询的结论.实验结果表明,并行DDR算法和文中优化算法针对顺序查询时都取得了较好的效果,且文中优化算法效果最好.这是因为:增加一次随机划分可以避免大数据块的出现而影响后续查询;文中优化算法可以针对不同的划分位置,选取更好的划分策略(两次Cracking-into-two操作或者一次Cracking-intothree操作),所以,文中算法比并行DDR算法性能有所提升.

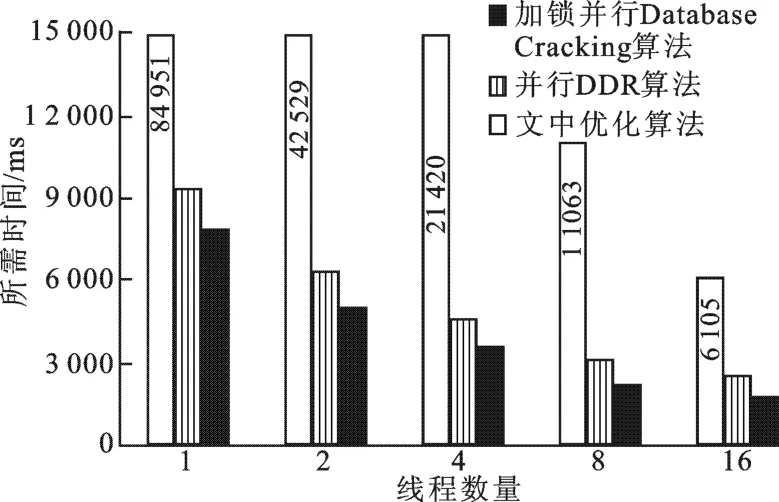
图10　算法鲁棒性优化实验结果

4　结束语

为了解决多核并行自适应索引算法不能高效地利用多核处理器的并行资源,且不能较好处理顺序查询的问题,笔者优化了传统的多核并行自适应索引算法.在改进Refined Partition Merge算法的基础上,将加锁并行方法与改进的Refined Partition Merge算法相结合,在索引中数据块较少时,使用优化的Refined Partition Merge算法,降低线程之间冲突的概率,减少线程等待时间,提高线程利用率.当索引中数据块较多时,使用加锁并行方法,充分利用了多核处理器的并行资源,且提高了算法的鲁棒性.实验证明了笔者提出方法的有效性和鲁棒性.

[1]马艳萍,姬光荣,邹海林,等.数据依赖的多索引哈希算法[J].西安电子科技大学学报,2015,42(4):159-164. MA Yanping,JI Guangrong,ZOU Hailin,et al.Data-oriented Multi-index Hashing[J].Journal of Xidian University,2015,42(4):159-164.

[2]LEIS V,KEMPER A,NEUMANN T.The Adaptive Radix Tree:Artful Indexing for Main-memory Databases[C]// Proceedings of the 29th International Conference on Data Engineering.Washington:IEEE Computer Society,2013: 38-49.

[3]IDREOS S,KERSTEN M L,MANEGOLD S.Database Cracking[C]//3rd Biennial Conference on Innovative Data Systems Research.Asilomar:CIDR,2007:68-78.

[4]GRAEFE G,HALIM F,IDREOS S,et al.Concurrency Control for Adaptive Indexing[J].Proceedings of the VLDB Endowment,2012,5(7):656-667.

[5]PIRK H,PETRAKI E,IDREOS S,et al.Database Cracking:Fancy Scan,Not Poor Man’s Sort[C]//10th International Workshop on Data Management on New Hardware.New York:ACM,2014:25-32.

[6]IDREOS S,MANEGOLD S,KUNO H,et al.Merging What’s Cracked,Cracking What’s Merged:Adaptive Indexing in Main-memory Column-stores[J].Proceedings of the VLDB Endowment,2011,4(9):585-597.

[7]GRAEFE G,KUNO H.Self-selecting,Self-tuning,Incrementally Optimized Indexes[C]//13th International Conference on Extending Database Technology.New York:ACM,2010:371-381.

[8]IDREOS S,KERSTEN M,MANEGOLD S.Updating a Cracked Database[C]//2007 ACM SIGMOD International Conference on Management of Data.New York:ACM,2007:416-424.

[9]SCHUHKNECHT F,JINDAL A,DITTRICH J.The Uncracked Pieces in Database Cracking[J].Proceedings of the VLDB Endowment,2014,7(2):97-108.

[10]HALIM F,IDREOS S,KARRAS P,et al.Stochastic Database Cracking:Towards Robust Adaptive Indexing in Mainmemory Column-stores[J].Proceedings of the VLDB Endowment,2012,5(6):502-513.

(编辑:王 瑞)

Optimizing the parallel adaptive indexing algorithm on multi-core CPUs

YUAN Tong,LIU Zhijing,LIU Hui
(School of Computer Science and Technology,Xidian Univ.,Xi’an 710071,China)

An improved parallel adaptive indexing algorithm on multi-core CPUs is proposed to solve the problems that the parallel adaptive indexing algorithms cannot take full advantage of the CMP’s parallel execution resource,and properly process the sequential query pattern.Based on the optimization of the Refined Partition Merge algorithm,our improved parallel adaptive indexing algorithm combines the Parallel Database Cracking method with the Refined Partition Merge algorithm.In our algorithm,when fewer data chunks are in the index,we use the optimized Refined Partition Merge algorithm so as to reduce the probability of conflict between threads,decrease the waiting time,and increase the utilization of the threads,and when more data chunks are in the index,we use the Parallel Database Cracking method so as to take full advantage of the CMP’s parallel execution resources.Besides,we propose an optimization for the robustness,which makes our algorithm suitable for two common query patterns.Experiments show that our method can reduce the query time by 25.7%～33.2%,and suit with common query patterns.

adaptive indexing;multicore processors;database cracking algorithm;database system

TP392

A

1001-2400(2016)05-0057-06

10.3969/j.issn.1001-2400.2016.05.011

2015-07-22 网络出版时间:2015-12-10

国家自然科学基金资助项目(61202177)

袁 通(1987-),男,西安电子科技大学博士研究生,E-mail:yuantongxd@gmail.com.

网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151210.1529.022.html