基于裂缝梁动力特性和自振频率的参数敏感性

石鲁宁， 闫维明， 何浩祥， 陈彦江

(北京工业大学工程抗震与结构诊治北京市重点实验室 北京, 100124)



基于裂缝梁动力特性和自振频率的参数敏感性

石鲁宁， 闫维明， 何浩祥， 陈彦江

(北京工业大学工程抗震与结构诊治北京市重点实验室 北京, 100124)

基于Bernoulli-Euler理论，将开口裂缝梁视为变截面梁，利用模态摄动方法建立了一种求解带任意数量开口裂缝简支梁和连续梁动力特性的半解析分析方法。在等截面无损梁的模态子空间内将裂缝梁的变系数微分方程的求解转化为非线性代数方程组的求解；利用无损梁的自振频率和振型函数摄动求解裂缝梁的模态参数；通过矩形开口裂缝简支梁和两跨连续梁的动力试验验证了笔者方法的准确性；最后，利用开口裂缝梁动力特性的半解析解研究了简支梁和两跨连续梁的自振频率对裂缝尺寸和位置的敏感性。

开口裂缝； 自振频率； 振型函数； 模态摄动法； 裂缝参数

引 言

简支梁和连续梁广泛应用于结构工程和机械工程中，在长期或者偶然荷载作用下不可避免的会出现损伤，而损伤的直接表现形式就是裂缝。裂缝的出现将会引起结构刚度的下降，进而引起结构自振频率、振型和阻尼等模态参数的变化。模态参数的变化还与裂缝的位置和尺寸有着密切关系[1-3]；通过模态参数的变化还可以对结构的损伤程度和位置进行识别。因此,研究裂缝梁的动力特性并分析裂缝参数对结构动力特性的影响具有重要的工程意义。

Dimarogonas等[1,4]基于断裂力学理论提出在裂缝梁的损伤位置利用无质量等效转动弹簧模拟裂缝，给出了弹簧刚度的计算公式，通过理论和试验研究了裂缝对结构动力特性的影响。Khiem等[5-6]利用转动弹簧模型和传递矩阵方法研究了带任意数目裂缝梁的动力特性，分析了裂缝数量和边界条件等对自振频率的影响。Krawczuk等[7]将裂缝等效为无质量的转动弹簧利用谱元方法研究了带裂缝Timoshenko梁的动力特性。Hamed等[8]研究了带裂缝预应力混凝土梁的非线性动力特性。Baris[9]利用转动弹簧模型研究了的轴向力下多个开口裂缝梁的振动问题。Zheng和Kisa等[10-11]利用有限元方法通过添加附加刚度矩阵反映结构的损伤进而获得损伤梁的自振频率和振型，分析了裂缝位置和深度对自振频率的影响。Cheng等[12-13]研究了呼吸裂缝梁的动力特性，但是呼吸裂缝梁的振动过程是非线性的，其分析方法与开口裂缝存在明显的不同。Zheng等[14]利用改进的Fourier级数方法研究了带任意数量开口裂缝Timoshenko梁的动力特性，分析了裂缝位置和尺寸对结构自振频率的影响。Torabi等[15-16]研究了变截面裂缝梁的动力特性，并分析了裂缝参数对结构动力特性的影响。Rezaee等[17]将裂缝梁简化为带弹簧质量阻尼的单自由度体系，采用摄动方法研究了呼吸裂缝简支梁的动力特性。郭智刚等[18-19]基于一阶摄动理论推导了带多条开口裂缝的欧拉梁的特征模态参数的理论计算公式，研究了简支梁和悬臂梁自振频率对裂缝参数的敏感性，但是文献[17-19]的研究不适用于连续梁也未考虑裂缝形式的影响在算法上与模态摄动方法也有明显的区别。Zheng等[20]利用改进的Rayleigh法获得损伤梁的频率方程，分析了裂缝参数对自振频率的影响。冀伟等[21]对波形钢腹板简支箱梁竖向频率的影响因素进行了分析。肖和业等[22]对变阻尼层复合梁动力特性进行了优化分析。综上所述，现有的裂缝模拟方法大致分两类：a.通过转动弹簧模拟裂缝;b.通过截面刚度的折减。裂缝梁振动方程的求解方法有：Fourier级数法、Rayleigh-Ritz法、传递矩阵法、能量法、摄动法和有限元法等。受制于裂缝模拟方法和振动方程求解方法，现有的针对于带任意数量开口裂缝连续梁的动力特性和裂缝参数对结构动力特性影响的研究尚不成熟。提出将开口裂缝梁视为变截面梁，基于模态摄动法给出了带任意数目开口裂缝简支梁和连续梁动力特性的半解析解，并通过试验验证了方法的准确性。利用裂缝梁动力特性的半解析解研究了裂缝参数对简支梁和连续梁动力特性的影响。

1 裂缝梁振动方程

1.1 裂缝梁动力特性计算模型

等截面n跨连续梁第i跨(1≤i≤n)损伤前后模型如图1所示。无损梁的惯性矩和面积分别为I0和A0，如图1(a)所示。连续梁共有N个矩形开口裂缝，其中第j个开口裂缝起点距坐标原点的距离为xj，裂缝宽度为bj，高度为hj，如图1(b)所示。

图1 裂缝梁模型Fig.1 The modal of crack beam

(1)

连续梁由无损状态转变为损伤状态惯性矩和面积的变化量为

(2)

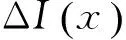
如图1(a)所示，无损梁的自由振动方程为

(3)

其中：EI为梁截面抗弯刚度；A为梁截面面积；ρ为密度；μ(x,t)为结构的位移。

如图1(b)所示，损伤梁的自由振动方程为

(4)

将式(2)代入式(4),整理得

(5)

定义矩形窗函数

(6)

将窗函数式(6)代入式(5),整理得

(7)

显然，损伤梁可看作是无损梁经过截面参数变化后得到的变截面梁。为了求解该变截面梁(损伤梁)的振动方程式(7)，可利用无损梁的模态参数摄动求解损伤梁的模态参数。

1.2 裂缝梁振动方程的求解

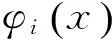
(8)

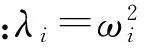
裂缝梁振动方程式(7)可采用变量分离方法求解，假定解的形式为

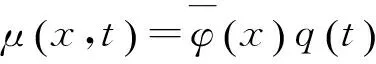
(9)

将式(9)代入式(7)，整理得

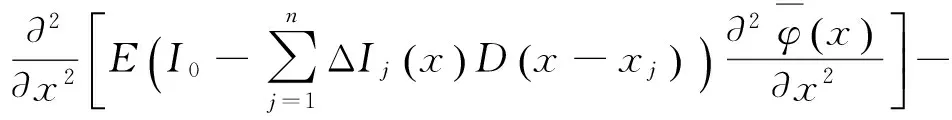
(10)

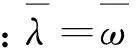
根据模态摄动理论[23]，把式(7)所表示的开口裂缝梁看作是如图1(a)所示的等截面无损梁经过截面惯性矩I0和面积A0变化后得到的新体系，这个新体系主模态函数及特征值可以利用无损梁的模态函数进行摄动求得。假设

(11)

(12)

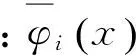
(13)

其中：qj为模态线性组合系数。

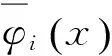
将式(11),(12)代入式(10)，利用式(8)进行简化整理得

(14)

(15)

其中

(16)

(17)

(18)

显然，式(16)～(18)需要利用无损梁的前η阶主模态参数进行积分获得，第2节将详细推导式(16)～(18)的具体表达式。

分别令式(15)中k=1,2, …,η，可获得η个关于未知数Δλi和qj(j=1,2,…,η;j≠i)的非线性代数方程，整理简化为矩阵形式如下

(19)

其中

其中：未知向量q的第i个元素qi=Δλi/λi。

这样,就把开口裂缝梁的变系数微分方程式(10)转化为非线性矩阵方程式(19)。本方法也适用于其他形式的开口裂缝梁动力特性的计算。

1.3 非线性方程组的求解

非线性矩阵方程组式(19)可采用Newton-Raphson法或遗传算法等并行智能算法求解，笔者采用Newton-Raphson法求解式(19)。Newton-Raphson法对于初值选取非常重要，给定合理的初值不仅可以减少迭代次数,还可以获得更加准确的收敛结果。根据式(19)的物理意义以及向量q内各组合系数的含义，给定q的初值为

q=0

(20)

迭代终止条件[19-20]可采用

(21)

其中：上角标κ为方程迭代次数；ξ为收敛误差。

将求得的未知向量q代入式(11)和式(12)，可获得开口裂缝梁的第i阶自振频率和振型。令式(11)和式(12)中i=1,2,…,n,重复迭代过程可获得开口裂缝梁的前n阶模态参数。

1.4 无损梁的频率方程和振型函数

为了求解式(19),首先需要获得等截面无损梁的自振频率和振型函数。根据文献[21],简支梁的第n阶频率方程和归一化振型函数为

(22)

(23)

其中：L为梁长。

连续梁的频率方程和振型函数可采用如下方法获得。取n跨等截面连续梁的第i跨梁段为研究对象，如图2所示。

图2 连续梁第i跨梁段模型Fig.2 The ith span beam

假设第i跨梁段起点i的转角位θi,i+1，弯矩为Mi,i+1，终点i+1处的转角位θi+1,i，弯矩为Mi+1,i，第i跨梁长Li。第i跨的自由振动方程为

(24)

第i(2≤i≤n-1)跨与相邻两跨的支座处的弯矩和转角需满足如下关系式

(25)

第一跨和最后一跨与其相邻跨的弯矩和转角需满足如下关系式

(26)

连续梁第i跨梁段的振型函数为

Cisinh(ax)+Dicosh(ax)

(27)

其中：ω2=a4EI/m；Ai，Bi，Ci和Di为实常数，可由梁端边界条件(位移、转角和弯矩)计算得到。

根据图2第i跨梁段梁端位移和弯矩分别为

(28)

将式(26)代入上述边界条件可得

(29)

将Ai,Bi,Ci和Di代入式(27)可得

(30)

对于支座i，由于Mi=Mi,i+1=Mi,i-1，则支座i(2≤i≤n)两侧转角可写为

(31)

n跨连续梁相邻两跨转角需满足θi,i-1=θi,i+1(2≤i≤n)，则由式(31)可得

(32)

取

整理式(32)得

(33)

将式(33)整理成矩阵形式，并利用n跨连续梁两端的弯矩M1=0，Mn+1=0，简化得

(34)

其中：M0=[M2,M3,…,Mn]T;

对于n跨连续梁在任意激励作用下，式(34)必存在非零解，则有

(35)

式(35)为n跨连续梁的频率方程。将ωi代入振型方程组式(30)即可求得n跨连续梁的第i阶振型。笔者给出两跨和三跨连续梁的振型函数表达式。

两跨连续梁第n阶振型函数

(36)

三跨连续梁第n阶振型函数

(37)

通过上述方法可获得n跨连续梁的频率方程和振型函数的表达式。将振型函数和自振频率代入式(16)～(18)通过求解即可获得非线性矩阵方程各系表达式。仅以带任意数量矩形开口裂缝简支梁为例给出了各系数的计算方法和具体表达式。

2 矩形开口裂缝简支梁系数的计算

2.1 系数mk的计算

将简支梁的振型函数式(23)代入式(16)积分,得到系数mk值为

(38)

2.2 系数Δkki的计算

根据文献[23]，式(17)可简化为

(39)

将式(2)代入式(18)，得

(40)

将式(23)代入式(40),积分可得

(41)

2.3 系数Δmki的计算

将式(2)代入式(18)，得

(42)

将简支梁振型函数式(23)代入式(42),积分可得

(43)

将系数mk，Δkki和Δmki值代入非线性矩阵方程组式(19)，通过求解式(19)即可获得开口裂缝梁的模态参数。对于两跨和三跨裂缝梁,需将振型函数式(36)和式(37)代入式(16)～(18),按同样的方法进行分段积分,即可获得系数mk，Δkki和Δmki值。

3 试验验证

通过矩形截面简支梁和两跨连续梁的动力试验对本方法获得的开口裂缝梁动力特性半解析解的准确性进行验证。钢梁截面为5 cm×5 cm，梁长为1.8 m；材料参数采用试验值，弹性模量为195 GPa，钢材密度为7 830 kg/m3。利用该钢梁同时做1.7 m简支梁和0.85 m+0.85 m两跨连续梁的动力试验。在简支梁和两跨连续梁动力试验的各个工况中7个轻质加速度传感器布置位置不变。试验中首先用橡胶锤施加激励以获取简支梁的振动响应，然后将中间支座固定于简支梁跨中位置用同样的方法采集两等跨梁的振动响应。裂缝采用切割机切割产生，首先在主裂缝位置分级切割，然后在次裂缝处分级切割。简支梁和两跨连续梁的高跨比分别为0.029 4和0.058 8，显然试验梁的高度远小于跨度属于Bernoulli-Euler梁，在裂缝梁动力特性计算中可以忽略转动惯量和剪切变形的影响。裂缝位置和传感器布置如图3(a)所示，简支梁和两跨连续梁的试验照片如图3(b)和3(c)所示。

试验采用锤击激励方式，裂缝采用切割机切割产生，信号采样频率为1 000 Hz。裂缝尺寸和试验工况如表1所示。图4为工况2简支梁和两跨连续梁的加速信号和频谱图。

将实测加速度信号进行傅里叶变换获得各工况试验梁的自振频率；利用Matlab软件编程求解非线性矩阵方程组式(19)。简支梁和两跨连续梁在不同

表1 裂缝尺寸和试验工况表 (单位：mm)

图3 试验梁图Fig.3 Test beam

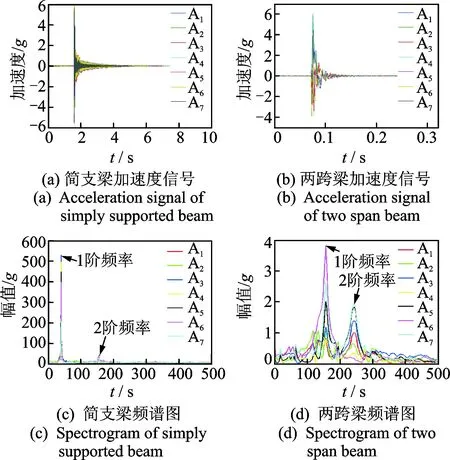
图4 试验梁振动信号处理Fig.4 The test results of signals

工况下的自振频率实测值和本方法计算值如表2,3所示。其中，简支梁在工况1下实测获得的结构1阶和2阶自振频率分别为39.10和156.40 Hz；两跨连续梁在工况1下实测获得的结构1阶和2阶自振频率分别为156.10和243.87 Hz。

表2 简支梁自振频率(单位：Hz)

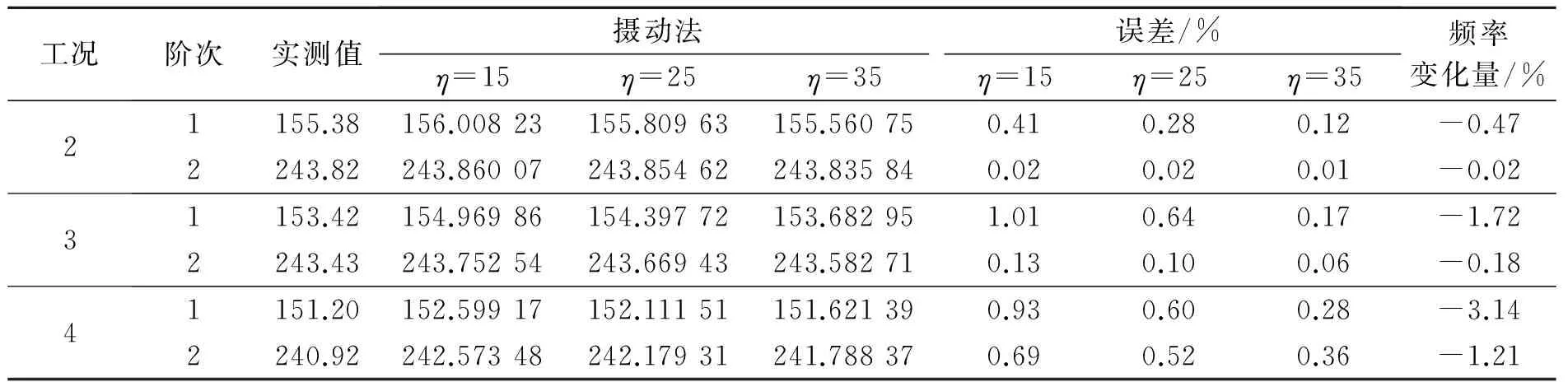
表3 两跨连续梁自振频率(单位：Hz)

由表2,3可知，摄动方法求得的矩形开口裂缝简支梁和两跨连续梁的前两阶自振频率与实测值较接近，随着损伤程度的增加摄动绝对误差稍有增大，但相对于损伤引起的频率变化量而言这种计算误差是比较小的，在实际工程中是可以接受的；当η=35时，摄动方法的最大误差仅有0.36%，当η=15时，最大误差也仅有1.01%。这表明本研究方法可以较准确地获得开口裂缝梁的模态参数。随着η值的增大摄动法计算结果趋向于实测值，理论上当η取值越大，计算结果越接近于真实值。笔者计算结果总是由较大值趋向于实测值；分析认为该方法属于Ritz法，计算结果总大于结构的真实值，计算精度取决于η的取值。本方法可较准确地获得开口裂缝梁的动力特性。

4 单裂缝对自振频率的影响

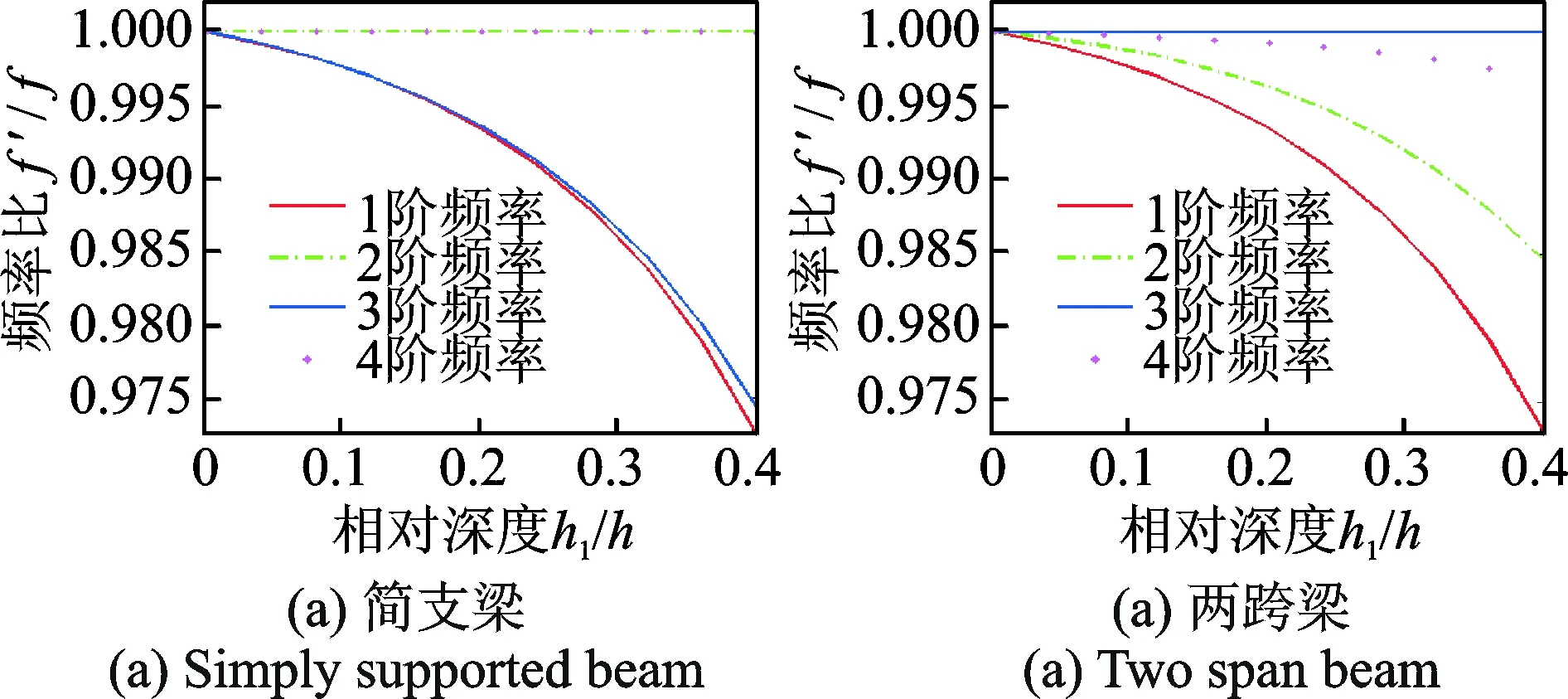
图5 裂缝深度对自振频率的影响Fig.5 Influence of crack depth on natural frequency

以试验梁为例，分析裂缝参数对简支梁和两跨连续梁自振频率的影响。假定开口裂缝宽度为15 mm，定义第i条裂缝的相对深度为hi/h，相对位置为xi/L，频率比为f′/f；h为梁高，L为梁长，f′为损伤梁自振频率，f为无损梁自振频率。图5给出了简支梁(x1/L=0.5)和两跨连续梁(x1/L=0.25)在跨中位置出现损伤，裂缝深度对裂缝梁前4阶自振频率的影响。由图5可知，简支梁跨中裂缝对第2，4阶自振频率几乎无影响，两跨梁跨中裂缝对第3阶自振频率几乎无影响。分析认为裂缝位置对自振频率的影响与振型函数值有内在的联系，当裂缝位于振型的反弯点位置时，裂缝对该阶自振频率几乎无影响，如图5简支梁的第2，4阶自振频率和两跨梁的第3阶自振频率；当裂缝位于振型的峰值处时，对该阶自振频率的影响较大，如图5简支梁的第1，3阶自振频率和两跨梁的第1，2阶自振频率。随着裂缝深度的增加各阶自振频率相应降低，其频率的变化量还与裂缝的位置有关。

当裂缝相对深度为h1/h=0.3时，裂缝位置对简支梁和两跨连续梁自振频率的影响如图6所示。分析认为简支梁裂缝位置对各阶自振频率的影响与其振型函数值存在联系；当裂缝位于振型峰值位置对该阶自振频率的影响较大，当裂缝位于振型的反弯点附近对该阶自振频率的影响微弱。对于两跨连续梁的奇数阶自振频率亦有此规律，但是对于两跨连续梁的偶数阶自振频率，当裂缝位于中间支座附近时自振频率的变化较大，分析认为两跨连续梁偶数阶振型为正对称振型，中间支座处转角为零，因此可将两跨梁简化为如图7所示结构计算其偶数阶振型。当裂缝位于两跨梁中间支座附近时，相当于图7梁体的固定端附近出现损伤，显然对自振频率的影响较大，本结论适用于偶数跨连续梁的偶数阶自振频率对裂缝参数的敏感性分析。通过上述分析可知,当偶数跨连续梁对称轴处梁体出现损伤时，利用频率对损伤程度进行评判时，建议采用偶数阶自振频率而不宜采用基频。

单个矩形裂缝深度和位置对简支梁和两跨连续梁自振频率的影响，如图8和图9所示。由图8和图9可以看出,不同裂缝深度和位置对简支梁和两跨连续梁前四阶自振频率的影响。

图8 简支梁裂缝深度和位置对自振频率影响Fig.8 Influence of crack location and crack depth on natural frequency of simply supported beam

图9 两跨梁裂缝深度和位置对自振频率影响Fig.9 Influence of crack location and crack depth on natural frequency of two span beam

通过研究多个裂缝对简支梁和两跨梁自振频率的影响，结果表明裂缝数量的变化并没有改变裂缝参数对自振频率的影响规律。本方法也适用于其他裂缝形式损伤梁动力特性的求解；将损伤梁截面惯性矩和面积的函数表达式代入式(16) ～(18)进行积分，获得参数mk，Δkki和Δmki值，通过求解式(19)即可获得裂缝梁的模态参数。

5 结束语

基于Bernoulli-Euler理论，将开口裂缝梁视为变截面梁，利用模态摄动方法获得了带任意数量开口裂缝简支梁和连续梁动力特性的半解析解。给出了等截面连续梁动力特性的解析解，推导了非线性代数方程组系数矩阵的具体表达式。通过矩形开口裂缝简支梁和两跨连续梁的动力试验验证了本方法的准确性。利用开口裂缝梁动力特性的半解析解研究了简支梁和两跨连续梁的自振频率对裂缝尺寸和位置的敏感性。不同的裂缝的深度和位置对结构模态参数的影响也是不同的。通常随着裂缝深度的增加，自振频率会出现下降，其变化规律与振型函数值有关；但自振频率的变化量与裂缝出现的位置有着密切关系。当偶数跨连续梁对称轴处梁体出现损伤时，利用频率对损伤程度进行评判时，建议采用偶数阶自振频。

[1] Dimarogonas A D. Vibration of cracked structures: a state of the art review[J]. Engineering Fracture Mechanics, 1996, 55(5):831-857.

[2] Shifrin E I. Ruotolo R. Natural frequencies of a beam with an arbitrary number of cracks[J]. Journal of Sound and Vibration, 1999, 222(3):409-423.

[3] Mazanoglu K, Yesilyurt I, Sabuncu M. Vibration analysis of multiple-cracked non-uniform beams[J]. Journal of Sound and Vibration, 2009, 320 (1):977-989.

[4] Chondros T G, Dimarogonas A D, Yao J. A continuous cracked beam vibration theory[J]. Journal of Sound and Vibration, 1998, 215(1):17-34.

[5] Khiem N T, Lien T V. A simplified method for natural frequency analysis of a multiple cracked beam[J]. Journal of Sound and Vibration, 2001, 245(4):737-751.

[6] Lin H P, Chang S C, Wu J D. Beam vibrations with an arbitrary number of cracks[J]. Journal of Sound and Vibration, 2002, 258(5): 987-999.

[7] Krawczuk M, Palacz M, Ostachowicz W. The dynamic analysis of a cracked Timoshenko beam by the spectral element method[J]. Journal of Sound and Vibration, 2003, 264(2):1139-1153.

[8] Hamed E, Frostig Y. Free vibrations of cracked prestressed concrete beams[J]. Engineering Structures, 2004, 26(1):1611-1621.

[9] Binici B. Vibration of beams with multiple open cracks subjected to axial force[J]. Journal of Sound and Vibration, 2005, 287(1):277-295.

[10]Kisa M, Brandon J. The effects of closure of cracks on the dynamics of a cracked cantilever beam[J]. Journal of Sound and Vibration, 2000, 238(1):1-18.

[11]Zheng D Y, Kessissoglou N J. Free vibration analysis of a cracked beam by finite element method[J]. Journal of Sound and Vibration, 2004, 273(1):457-475.

[12]Carr G E, Jaureguizahar L F, Chapetti M D. Analysis of breathing cracks using vibrations[J]. Experimental Techniques, 2013, 37(1):32-40.

[13]Cheng S M, Wu X J, Wallace W. Vibrational response of a beam with a breathing crack[J]. Journal of Sound and Vibration, 1999, 225(1):201-208.

[14]Zheng D Y, Fan S C. Natural frequency changes of a cracked Timoshenko beam by modified fourier series [J]. Journal of Sound and Vibration, 2001, 246(2):297-317.

[15]Torabi K, Afshari H, Aboutalebi F H. A DQEM for transverse vibration analysis of multiple cracked non-uniform Timoshenko beams with general boundary conditions[J]. Computers and Mathematics with Applications, 2014, 67(1):527-541.

[16]Yanga J, Chena Y, Xiang Y, et al. Free and forced vibration of cracked inhomogeneous beams under an axial force and a moving load[J]. Journal of Sound and Vibration, 2008, 312(1):166-181.

[17]Rezaee M, Hassannejad R. Free vibration analysis of simply supported beam with breathing crack using perturbation method[J]. Acta Mechanica Solida Sinica, 2010, 3(5):460-470.

[18]郭智刚, 孙智.基于摄动法的多条裂纹欧拉梁特征模态分析[J]. 振动与冲击, 2013, 32 (10):1-6.

Guo Zhigang, Sun Zhi. Modal analysis of Euler- Bernoulli beam with multiple open cracks based on perturbation method[J]. Journal of Vibration and Shock, 2013, 32(10):1-6. ( in Chinese)

[19]徐平.局部裂纹损伤简支梁的曲率模态特性[J]. 固体力学学报, 2011, 32(1):171-175.

Xu Ping. Modal curvature characteristics of a simple beam with a local damaged crack[J]. Chinese Journal of Solid Mechanics, 2011, 32(1):171-175. ( in Chinese)

[20]Zheng Tianxin, Ji Tianjian. An approximate method for determining the static deflection and natural frequency of a cracked beam[J]. Journal of Sound and Vibration, 2012, 331(1):2654-2670.

[21]冀伟, 刘世忠. 波形钢腹板简支箱梁竖向频率的影响因素分析[J]. 振动、测试与诊断, 2013, 33(6):1039-1043.

Ji Wei, Liu Shizhong. Influencing factors of vertical frequency of the box beam with corrugated steel webs[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(6):1039-1043. ( in Chinese)

[22]肖和业, 盛美萍, 陶红丹. 变阻尼层复合梁动力特性的优化分析[J]. 振动、测试与诊断, 2010, 30(1):43-46.

Xiao Heye, Sheng Meiping, Tao Hongdan. Optimization analysis of dynamic characteristics of damping-variable composite beam[J]. Journal of Vibration, Measurement & Diagnosis, 2010, 30(1):43-46. (in Chinese)

[23]Lou M L, Duan Q H, Chen G.Modal perturbation method for the dynamic characteristics of Timoshenko beams[J]. Shock and Vibration, 2005, 12(6):425-434.

10.16450/j.cnki.issn.1004-6801.2016.05.010

国家自然科学基金资助项目(51378039，51378037，51478024)

2014-08-21；

2014-10-22

TU311.3; TH82

石鲁宁，男，1987年5月生，博士生。主要研究方向为结构振动与健康监测。曾发表《带任意附加质量的变截面弹性支承梁动力特性的解析解》(《工程力学》，2016年第33卷第1期)。

E-mail: shiluning1987@163.com

简介： 闫维明,男，1960年5月生，博士、教授。主要研究方向为结构监测及控制。

E-mail: yanwm@bjut.edu.cn