含支承松动故障的航空发动机非同步响应特征

王海飞, 陈 果, 廖仲坤， 张 璋， 邵伏勇

(1.南京航空航天大学民航学院 南京，210016) (2.中国航天科工飞航技术研究院北京动力机械研究所 北京，100074)



含支承松动故障的航空发动机非同步响应特征

王海飞1, 陈 果1, 廖仲坤2， 张 璋2， 邵伏勇2

(1.南京航空航天大学民航学院 南京，210016) (2.中国航天科工飞航技术研究院北京动力机械研究所 北京，100074)

针对航空发动机支承系统中普遍存在的松动故障，为研究松动故障导致的非同步响应特征产生的机理，建立了发动机的转子-支承-机匣整机模型，引入支承松动故障模型，利用数值积分方法求解耦合系统的响应，分析了非同步响应特征。结果表明，对于航空发动机中的支承松动故障，其引发的分频以及倍频原因在于，当刚度变化的周期等于转速周期时，将产生转频的倍频现象，在特定转速下，将激发系统的临界转速对应的频率；当刚度变化的周期等于n倍的转速周期时，则将产生1/n转频的分频及其倍频，在特定转速下，将激发系统的临界转速对应的频率。

非同步响应特征； 动力学建模； 松动故障； 整机振动； 松动机理

引 言

支承松动故障是航空发动机中的常见故障，当松动故障存在时，在不平衡激励下，转子将被周期地抬起，进而导致转静碰摩。研究松动故障导致的倍频以及分频产生机理具有重要意义。

针对松动单一故障，很多学者进行大量研究。Ehrich[1]使用单自由度模型，采用分段线性函数描述支承非线性，研究了亚临界、通过临界以及超临界下转子的非同步响应特征。陈予恕等[2-3]采用新方法对单自由度、两个自由度非线性系统的亚/超共振进行研究。肖锡武等[4]对不对称转子系统的刚度系统周期性变化的非线性振动问题，采用多尺度法研究了1/2亚谐共振-主共振，采用奇异性理论分析分叉响应方程和定常解的稳定性。姜忻良等[5]对三个自由度体系，采用多尺度法研究了超谐共振与亚谐共振。张嘉欣等[6]采用谐波平衡法研究了无定心弹簧刚性转子-挤压油膜阻尼器轴承(SFDB)系统非同步稳态响应的稳定性。陈安华等[7]利用多尺度法分析了刚度非线性转子系统的横向振动，论证了当转频接近线性化固有频率的1/2或1/3时，分别存在明显的二阶或三阶超谐共振现象。张靖等[8]采用非稳态非线性油膜力公式，建立了转子-轴承系统中两端支座与基础之间同时出现松动情况简单的转子数学模型。段吉安等[9]等建立了一个松动故障的非线性力学模型，既考虑了松动故障因刚度分段变化引起的强非线性特征，还考虑了松动故障存在间隙时对系统产生的周期性冲击作用。Chu等[10]分析了带有支座松动的转子-轴承系统振动特征，采用打靶法求取系统的周期解以及Floque理论分析周期解的稳定性。刘献栋等[11]建立了针对滚动轴承转子系统松动故障模型，得出小波变换不但能很好地诊断滚动轴承-转子系统的支承松动故障，而且能比Fourier变换在更低转速下诊断出转子系统的松动故障。任朝晖等[12]基于有限元理论，研究了松动故障对双盘悬臂转子-轴承系统非线性动力学特性的影响。

近年来，很多学者对含松动故障的耦合故障也进行了大量研究。Muszynska等[13]建立了一端不平衡，轴承座松动以及转静间碰摩转子-轴承-静子模型，展示出周期运动，分数次周期以及倍周期非线性特征。罗跃纲等[14]建立了带有基础松动-碰摩耦合故障的具有三轴承支承的双跨弹性转子系统的动力学模型，并对系统非线性动力学特性进行了数值仿真研究。刘杨等[15]等建立了双盘三支撑的松动-碰摩耦合故障转子系统力学模型和有限元模型，发现松动-碰摩耦合转子常常以碰摩故障特征为主，并且时域波形高矮峰交替出现，轴心轨迹呈现“梯形”。周鹏等[16]利用非线性动力学及转子动力学建立了松动发展的模型，找到松动-碰摩的特点和规律。

由于航空发动机机匣普遍采用薄壁结构，支承刚度较低，柔度较大，松动现象普遍存在。当航空发动机在亚临界、通过临界以及超临界转速下，出现的倍频与分频成分，没有进行详细的分析，为了更好地理解松动故障的本质，分析松动故障的非同步响应特征具有重要意义。笔者通过对含松动故障的某型发动机整机模型数值仿真求得响应特征，揭示了含松动故障的系统的非同步响应特征规律。

1 某型发动机整机动力学模型

1.1 某型发动机整机模型示意图

图1为某型发动机的转子-支承-机匣模型示意图。该发动机的尺寸通过UG软件从发动机的三维数模中测量得到。

图1 某型发动机的转子-支承-机匣模型示意图 (单位：mm)Fig.1 Rotor-bearing-Casing model sketch map of a type of aero-engine (unit: mm)

图中:P1为风扇盘;P2为发电机旋转部件(磁钢);P3为压气机盘;P4,P5分别为涡轮盘1，2；C1为机匣；G1为风扇轴与传动轴套齿联轴器;G2为传动轴与压气机轴套齿联轴器;G3为压气机轴与涡轮轴套齿联轴器；S1为风扇支点;S2为压气机前支点;S3为压气机后支点;S4为涡轮支点；I1，I2分别为前、后安装节；kg为齿轮泵啮合刚度;kf1,kf2,kf3,kf4为转子-机匣支承刚度；kc为机匣-基础连接刚度；T1为压气机前支点测点。该发动机为单转子，多段轴采用花键连接等特点，支撑类型为0-2-2-0。

1.2 动力学建模

转子模型和机匣模型利用有限元梁模型[17-18]，转子通过力和力矩与其他转子、机匣以及支承耦合。具体建模方法参考文献[18]。

转子系统的运动方程为

(1)

其中:Qs为系统承受的载荷；Ms为系统的质量矩阵；Gs为系统的陀螺力矩矩阵；Ks为系统的刚度矩阵；Cs为系统的阻尼矩阵。

本研究采用比例阻尼，即Cs=α0Ms+α1Ks，可以得到第i阶阻尼比为

(2)

通过转子任意两阶固有频率和阻尼比，求出α0,α1，求得系统的阻尼矩阵Cs。

1.2.1 支承松动故障建模

设转子和机匣之间的等效刚度为kf0，kf0=5×107N/m，该值通过经验估计。在相对位移条件下，考虑转子与机匣间的分段线性，则分段刚度kf为

(3)

其中：xr为转子位移；xc为机匣位移；刚度方向为x向和y向。

本研究仅考虑水平方向的松动，假设接触软弹簧，接触情况标记为1，接触硬弹簧，接触标记为-1。1.2.2 时域数值求解方法

由于转子-支承-机匣耦合系统高度非线性，因此采用数值积分方法求解。笔者利用Newmark-β法对转子和机匣有限元模型进行求解，求得转子和机匣响应，再利用支承松动故障模型求得支承力，将支承力作用到转子和机匣。流程图如图2所示。

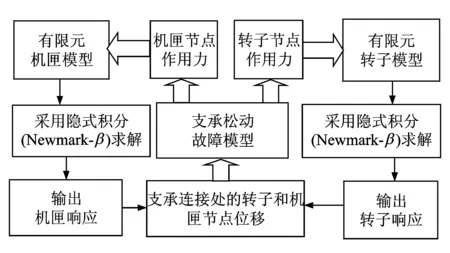
图2 转子-支承-机匣动力学求解流程图Fig.2 Solving flow for rotor-support-casing coupling dynamics

2 松动故障仿真分析

2.1 动力学模型参数

转子与机匣有限元参数以及转子-机匣-支承连接参数如表1～4所示。其中：风扇转子的外径为30 mm；压气机转子的外径为37.6 mm；涡轮转子的外径为49 mm；内径均为0 mm；机匣的外径为260 mm，内径为230 mm。所有联轴器径向刚度为1×108N/m，角向刚度为1×104N·m/rad。

表1 转子与机匣单元数

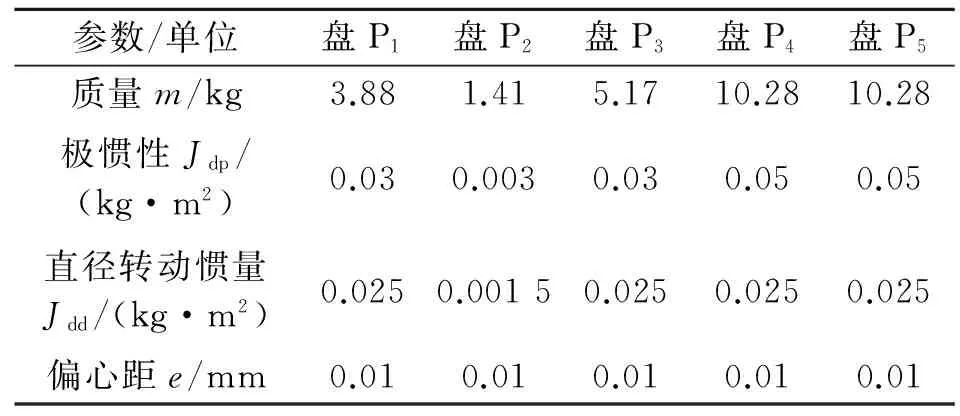
表2 转盘参数

表3 转子-机匣支承参数

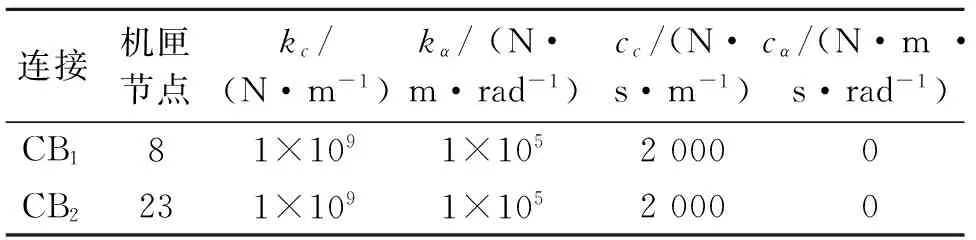
表4 机匣-基础连接参数

2.2 计算条件

1) 考虑压气机前支点处的转子和机匣之间的水平方向的支承松动。

2) 输出为机匣在压气机前支点处的水平方向的振动加速度响应。

3) 转速范围为15～70 kr/min。

2.3 临界转速计算

图3为仅含不平衡故障下，机匣节点9横向加速度的振幅-转速曲线，从图中可以看出，前三阶临界转速分别为26.4,52.2,66.9 kr/min。为获取松动故障的响应特征，且整机振动验证实验较困难，故未对整机特性进行验证。

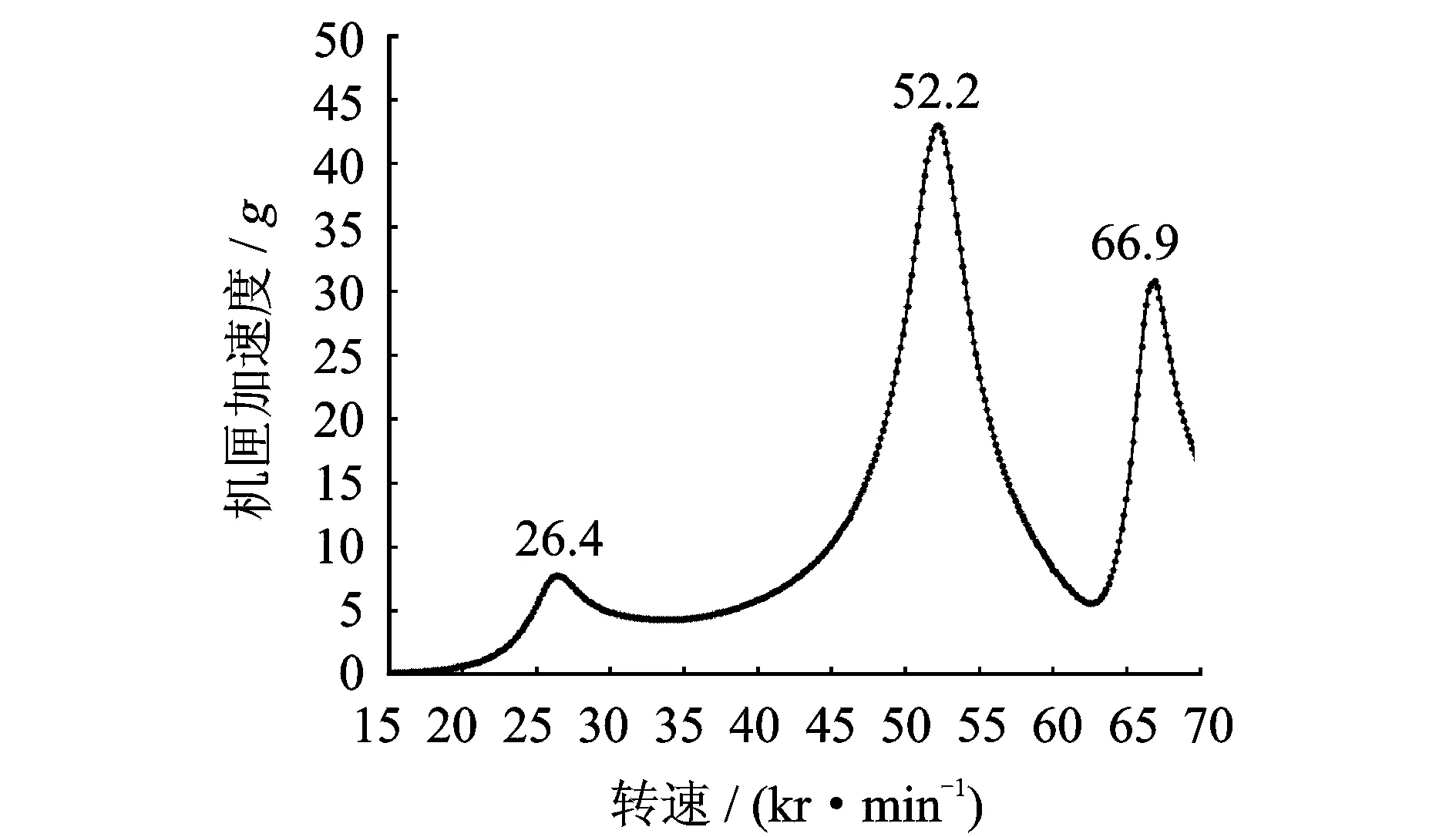
图3 机匣横向加速度振幅-转速曲线Fig.3 Amplitude-speed curve of casing lateral acceleration

2.4 不同转速下的机匣加速度特征分析

图4 在15～70 kr/min下机匣加速度的3维瀑布图Fig.4 Spectrum cascade of the casing acceleration response under 15～70 kr/min

图4为松动故障下，机匣节点9的横向加速度的3维瀑布图。从图中可以看出，在前3阶临界转速附近下，即对应于440，920以及1 115 Hz，出现较大的转频成分，同时激发了较大的系统的超谐共振以及亚谐共振。当转速为17.4 kr/min时，即1/3倍的第2阶临界转速，出现倍频成分，且3倍频较大，即系统的第2阶临界转速对应的频率。当转速为22.2 kr/min时，即1/3倍的第3阶临界转速，出现倍频成分，且3倍频较大，即系统的第3阶临界转速对应的频率。当转速为27.6 kr/min时，即1/2倍的第2阶临界转速下，出现倍频成分，且2倍频较大，即系统的第2阶临界转速对应的频率。当转速为35.25 kr/min时，即5/4倍的第1阶临界转速下，出现倍频成分，3/4分频成分，即系统的第1阶临界转速对应的频率。当转速为54.75 kr/min时，即2倍的第1阶临界转速下，出现倍频成分，1/2分频成分，即系统的第1阶临界转速对应的频率。当转速为67.35 kr/min时，即1倍的第1阶临界转速下，出现倍频成分，1/3分频成分。

2.5 典型转速下非同步响应特征分析

为了突显转子系统响应中的转频及其倍频和分频的周期成分，笔者采用自相关降噪方法对机匣加速度信号进行降噪。

图5 1/3第2阶临界转速(17 400 r/min)的波形特征Fig.5 The waveform features at 1/3 times of the second order critical speed

图5～9分别是转速为17.4，22.2，27.6，35.25，54.75,67.35 kr/min时的结果。在图5(a)～(d)中，机匣加速度降噪后每个旋转周期内时域波形有3次冲击。降噪后的频谱出现了转频以及较强的转频的3倍频成分。在图5(e)中，相对位移在每个旋转周期内时域波形有2次跳跃，有2个波峰，由于该模型中的阻尼较大，使得跳跃次数减少。在图5(f)中，接触位置在每个旋转周期内，刚度变化一次，刚度变化的周期等于转速周期，从而产生了转频的倍频成分。

在图6(a)～(d)中，机匣加速度降噪后每4个旋转周期内时域波形有3次冲击。降噪后的频谱出现了转频以及较强的转频的3倍频成分以及非同步频率成分；在图6(e)中，相对位移在每个旋转周期内时域波形有两次跳跃，有两个波峰，由于该模型中的阻尼较大，使得跳跃次数减少。在图6(f)中，接触位置在每个旋转周期内，刚度变化一次，刚度变化的周期等于转速周期，从而产生了转频的倍频成分。

图6 1/3第3阶临界转速(22 200 r/min)的波形特征Fig.6 The waveform features at 1/3 times of the third order critical speed

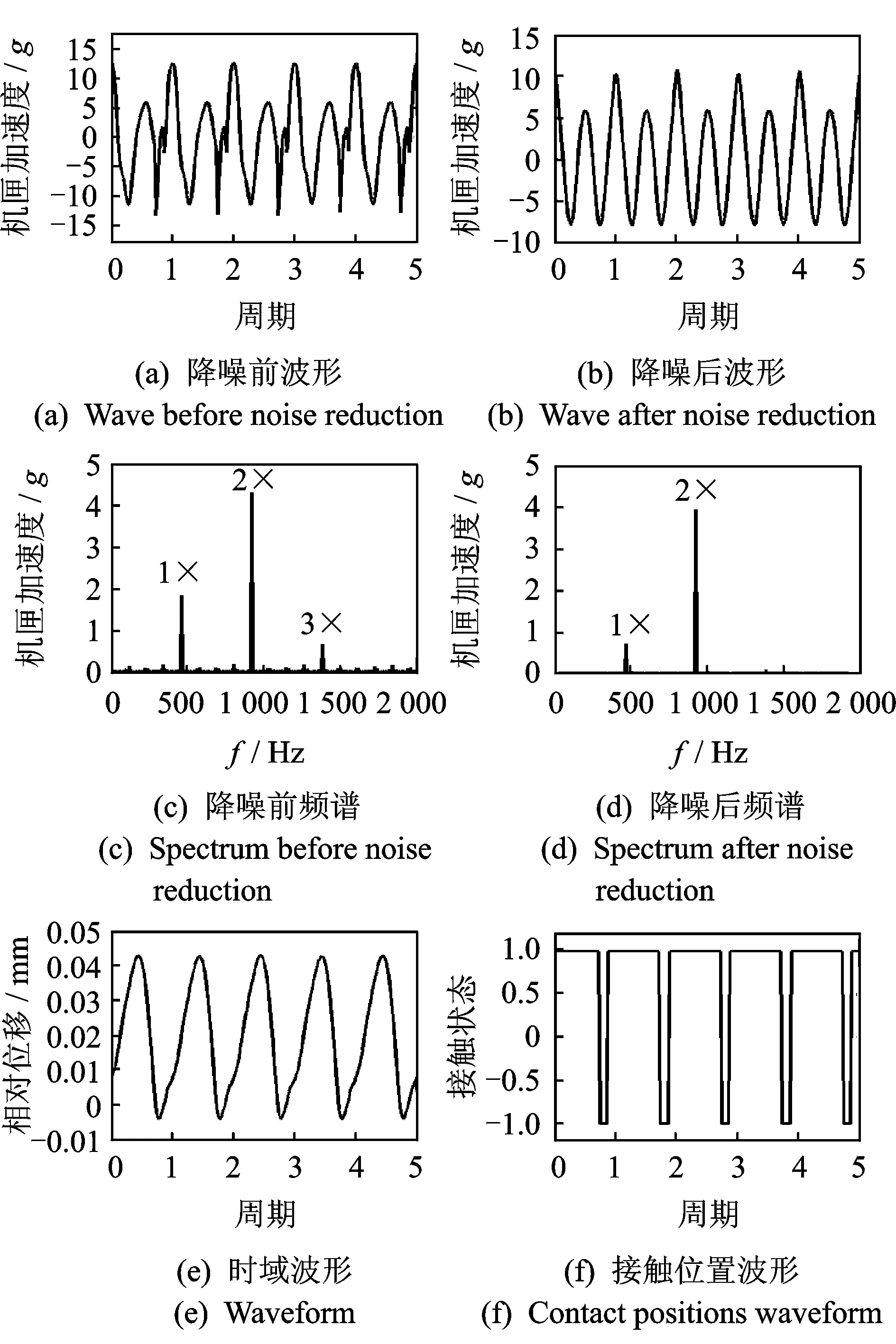
图7 1/2第2阶临界转速(27 600 r/min)的波形特征Fig.7 The waveform features at 1/2 times of the second order critical speed

在图7(a)～(d)中，机匣加速度降噪后每个旋转周期内时域波形有两次冲击；降噪后的频谱出现了转频以及较强的转频的2倍频成分；在图7(e)中，相对位移在每个旋转周期内时域波形有一次跳跃，由于该模型中的阻尼较大，使得跳跃次数减少。在图7(f)中，接触位置在每个旋转周期内，刚度变化一次，刚度变化的周期等于转速周期，从而产生了转频的倍频成分。

在图8(a)～(d)中，机匣加速度降噪后每4个旋转周期内时域波形有5次冲击。降噪后的频谱出现了转频、转频的倍频以及非同步频率成分。在图8(e)中，相对位移在每4个旋转周期内时域波形有3次跳跃，由于该模型中的阻尼较大，使得跳跃次数减少。在图8(f)中，接触位置在每4个旋转周期内，刚度变化3次，刚度变化的周期等于转速周期的4倍，从而产生了转频的1/4分频成分。

图8 5/4第1阶临界转速(35 250 r/min)的波形特征Fig.8 The waveform features at 5/4 times of the first order critical speed

在图9(a)～(d)中，机匣加速度降噪后每两个旋转周期内时域波形有两次冲击。降噪前的频谱出现了转频以及1/2倍转频成分，由于1/2倍转频成分较弱，降噪后相对于转频不明显。在图9(e)中，相对位移在每两个旋转周期内时域波形有两次跳跃，由于该模型中的阻尼较大，使得跳跃次数减少。在图9(f)中，接触位置在每个旋转周期内，刚度变化一次，刚度变化的周期等于转速周期的两倍，从而产生了转频的1/2分频成分。

图9 2倍第1阶临界转速(54 750 r/min)的波形特征Fig.9 The waveform features at two times of the first order critical speed

在图10(a)～(d)中，机匣加速度降噪后每3个旋转周期内时域波形有3次冲击。降噪后的频谱出现了转频、1/3倍转频成分以及非同步频率成分。在图10(e)中，相对位移在每两个旋转周期内时域波形有3次跳跃，由于该模型中的阻尼较大，使得跳跃次数减少。在图10(f)中，接触位置在每3个旋转周期内，刚度变化两次，刚度变化的周期等于转速周期的3倍，从而产生了转频的1/3分频成分。

图10 1倍第3阶临界转速(67 350 r/min)的波形特征Fig.10 The waveform features at the third critical speed

图5～图7表明，当刚度变化的周期等于转速变化的周期，引起伪临界超谐共振，且激发系统的临界转速对应的频率。图8～图10表明，刚度变化的周期等于转速变化的周期的倍数，引起伪临界亚谐共振，且激发系统的临界转速对应的频率。

3 结束语

针对某型发动机，建立了含松动故障的发动机整机动力学模型，并利用时域数值积分法进行了非线性响应求解，得到了松动故障下机匣加速度响应。发现了在分数阶临界转速对应的频率以及临界转速对应的频率下激发系统的亚谐共振与超谐共振。在典型转速下，转频、倍频以及非同步频率成分，且激发较大的系统的临界转速对应的频率，解释了其产生的原因。

发动机中的松动故障所引起的亚谐共振以及超谐共振原因在于，松动故障引起了转速周期内刚度周期变化，当刚度变化的周期等于转速周期时，将产生倍频现象，在特定转速下，将激发系统的临界转速对应的频率；当刚度变化的周期等于n倍转速周期时，则将产生1/n分频及其倍频，在特定转速下，将激发系统的临界转速对应的频率。

[1] Ehrich F F. A new class of asynchronous rotor dynamic response in high-speed rotors[C]∥Proceedings of the ASME 2007 Design Engineering Technical Conferences & Computers and Information in Engineering Conference. Las Vegas , Nevada, USA： [s.n.], 2007:1783-1788.

[2] 陈予恕, 李世海. 二阶非线性微分方程亚/超谐共振的一种求解方法及其应用研究[J]. 力学学报, 1986,18(4):341-349.

Chen Yushu, Li Shihai. A method for finding the sub/super harmonic resonance solution of second order nonlinear differential equation and its application[J]. Acta Mechanica Sinica, 1986, 18(4):341-349. (in Chinese)

[3] 陈予恕, 金志胜. 两自由度分段线性振动系统的亚谐解[J]. 应用数学和力学, 1986,7(3):205-213.

Chen Yushu, Jin Zhisheng. Subharmonic solution of a piecewise linear oscillator with two degrees of freedom[J]. Applied Mathematics and Mechanics, 1986, 7(3):205-213. (in Chinese)

[4] 肖锡武, 杨正茂, 肖光华,等. 不对称转子系统的非线性振动[J]. 华中科技大学学报, 2002,30(5):81-84.

Xiao Xiwu, Yang Zhengmao, Xiao Guanghua, et al. Nonlinear oscillations of an unsymmetrical rotor system[J]. Journal of Huazhong University of Science & Technology, 2002, 30(5):81-84. (in Chinese)

[5] 姜忻良, 骆兰月. 考虑非对称效应的非线性结构超谐共振与亚谐共振[J]. 地震工程与工程振动, 2003,23(5):50-56.

Jiang Xiliang, Luo Lanyue. Superharmonic resonance and subharmonic resonance of nonlinear structures considering nonsymmetrical effect[J]. Earthquake Engineering and Engineering Vibration, 2003, 23(5):50-56. (in Chinese)

[6] 张嘉欣, 薛中擎. 无定心弹簧刚性转子-SFDB系统非同步稳态响应的稳定性分析[J]. 航空动力学报, 1991,6(3):277-283.

Zhang Jiaxin, Xue Zhonging. Stability analysis of a rigid rotor on SFDB without a centralizing spring[J]. Journal of Aerospace Power, 1991, 6(3):277-283. (in Chinese)

[7] 陈安华, 钟掘. 转子系统超谐波共振的理论分析与实验研究[J]. 中南工业大学学报, 1997,28(3):270-273.

Chen Anhua, Zhong Jue. The theoretical analysis and experimental research into super harmonic resonances of rotor systems[J]. Journal of Central South University of Technology, 1997, 28 (3):270-273. (in Chinese)

[8] 张靖, 闻邦椿. 带有两端支座松动故障的转子系统的振动分析[J]. 应用力学学报, 2004,21(3):67-72.

Zhang Jing, Wen Bangchun. Vibration characteristics of a rotor system with pedestal looseness at two supports[J]. Chinese Journal of Applied Mechanics, 2004, 21(3):67-72. (in Chinese)

[9] 段吉安, 黄志开. 旋转机械松动故障的非线性力学模型[J]. 中南工业大学学报, 2002,33(1):78-81．

Duan Ji′an, Huang Zhikai. Nonlinear model of rotor system with loose fault[J]. Journal of Central South University of Technology, 2002, 33(1):78-81. (in Chinese)

[10]Chu Fulei, Tang Yun. Stability and Non-linear responses of a rotor-bearing system with pedestal looseness[J]．Journal of Sound and Vibration, 2001, 241(5):879-893．

[11]刘献栋, 何田, 李其汉. 支承松动的转子系统动力学模型及其故障诊断方法[J]. 航空动力学报, 2005, 20(1):54-59.

Liu Xiandong, He Tian, Li Qihan. Dynamic model of rotor system with support loosening and its diagnosis method[J].Journal of Aerospace Power, 2005, 20(1):54-59.(in Chinese)

[12]任朝晖, 陈宏, 马辉,等.双盘悬臂转子-轴承系统基础松动故障分析[J]. 农业机械学报, 2007,38(11):196-201.

Ren Zhaohui, Chen Hong, Ma Hui, et al. Pedestal looseness fault analysis of a vertical dual-disk over-hung rotor-bearing system[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(11):196-201.(in Chinese)

[13]Muszynska A, Goldman P. Chaotic responses of unbalanced rotor bearing stator systems with looseness or rubs[J]．Chaos, Solitons and Fractals,1995,5(9):1683-1704．

[14]罗跃纲, 杜元虎, 任朝晖,等. 双跨转子-轴承系统松动-碰摩耦合故障的非线性特性[J]. 农业机械学报，2008,39(11):180-183.

Luo Yuegang, Du Yuanhu, Ren Zhaohui, et al. Nonlinear characteristics of two-span rotor-bearing system with coupling faults of pedestal looseness and rub-impact[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(11):180-183. (in Chinese)

[15]刘杨, 太兴宇, 马辉,等.双盘三支撑转子轴承系统松动/碰摩耦合故障分析[J]. 航空动力学报, 2013,28(5):977-982.

Liu Yang, Tai Xingyu, Ma Hui, et al. Looseness-rubbing coupling fault of dual-disk three-supporting rotor-bearing system[J]. Journal of Aerospace Power, 2013,28(5):977-982. (in Chinese)

[16]周鹏, 刘挺, 冯霏,等. 松动-碰摩发展过程中的非线性满变问题[J]. 振动、测试与诊断, 2012, 32(增刊)：123-125.

Zhou Peng, Liu Ting, Feng Fei, et al. Nonlinear slowly varying problems in development process of loose-rubbing[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(S):123-125. (in Chinese)

[17]陈果. 航空发动机整机振动耦合动力学模型及其验证[J]. 航空动力学报, 2012,27(2):242-254.

Chen Guo. A coupling dynamic model for whole aeroengine vibration and its verification [J]. Journal of Aerospace Power, 2012, 27(2):242-254.(in Chinese)

[18]《航空发动机设计手册》总编委会.航空发动机设计手册第19分册：转子动力学及整机振动[M].北京：航空工业出版社，2000:208-226.

10.16450/j.cnki.issn.1004-6801.2016.05.007

*国家安全重大基础研究资助项目(613139)；江苏省研究生培养创新工程资助项目(KYLX_0295);中央高校基本科研业务费专项资金资助项目

2014-08-09；

2014-12-23

TH113.1

王海飞，男，1986年3月生，博士生。主要研究方向为转子动力学和航空发动机整机振动分析。曾发表《Casing vibration response simulation analysis and its verification under the blade-casing rubbing fault》(《Journal of Vibration and Acoustics》2016,Vol.138,No.3)等论文。

E-mail：wanghaifei1986318@163.com