基于非线性光流方程的数字图像相关非迭代灰度梯度算法*

刘小勇 李荣丽 郝兆朋 王 晖 崔高健 范依航 宫 岩

(长春工业大学机电工程学院，吉林 长春 130012)



基于非线性光流方程的数字图像相关非迭代灰度梯度算法*

刘小勇 李荣丽 郝兆朋 王 晖 崔高健 范依航 宫 岩

(长春工业大学机电工程学院，吉林 长春 130012)

在传统的非迭代灰度梯度数字图像相关算法中，假设变形前后同一个像素点的灰度值相等。但在实际应用中，图像的采集会受到环境光照的变化、相机曝光过度/不足、加载引起被测表面图像变化等因素的影响而引起变形前后图像像素点灰度值的变化。针对这一问题，应用非线性光流方程来描述变形前后像素点间的灰度关系,从而提出一种基于非线性光流方程的非迭代灰度梯度算法。应用模拟实验与真实单轴拉伸实验对算法的有效性与计算精度进行验证。结果表明，该算法对图像的灰度变化不敏感，具有较高的测量精度。

数字图像相关；非线性光流方程；非迭代灰度梯度算法

经过近40年的发展，数字图像相关方法[1](简称DIC方法，又称为数字散斑相关方法[2])已成为一种较成熟的非接触全场变形光学计量方法，广泛应用于实验力学及其他相关科学研究与应用领域。在变形测量过程中，首先利用成像设备获得被测表面变形前后的散斑图像，然后应用数字图像相关算法通过跟踪变形前后散斑图中像素点的位置变化而获得位移及应变信息。

数字图像相关方法的计算求解过程通常分为两步，即首先进行快速整像素位移求解(整像素定位)，然后在整像素位移的基础上进行亚像素位移求解[3-4]。通常，对整像素位移求解的精度要求不高，只需达到1像素精度即可，且求解算法较简单易于实现。因此，国内外研究人员对DIC的亚像素位移求解算法开展了大量的研究工作，并取得了丰硕的成果。逐渐形成了以Newton-Raphson 算法(简称N-R算法)[5]、曲面拟合法[6]、基于梯度算法(即非迭代灰度梯度算法，简称NIGGA)[7]、灰度梯度迭代算法 (简称IGGA)[8]为代表的典型DIC算法。由文献[9-10]对上述4种经典算法的比较研究可知，N-R算法和IGGA方法具有较高的计算精度和稳定性，但在计算过程中这两种算法均为迭代计算求解而且需要求解相关函数的二阶梯度或灰度的一阶导数，所以这两种算法的计算效率较其他两种算法低。曲面拟合算法虽然计算速度较快，但其计算精度为此四种算法中最低。因此，在对计算效率无特殊要求的离线测量应用中推荐使用N-R算法和灰度梯度迭代算法；在计算精度与计算效率均有特殊要求时推荐使用非迭代梯度算法[4]。

传统的非迭代灰度梯度算法是在两幅变形前后的散斑图像上取相同的区域(通常称为子图像), 并根据运动图像序列分析中的光流法原理假设所取区域内对应像素点的灰度值相等(通常将这一等式关系也称为光流方程，如图1所示)，然后通过对光流方程的优化找到变形子图像的位置，进而获得待求点的位移向量。但在实际应用中，由于图像采集受照明变化、相机曝光过度或不足、加载引起被测表面图像变化等因素的耦合影响，变形前后散斑图的灰度值不再是简单的相等关系。因此，本文将变形前后散斑图灰度的非线性关系模型引入传统光流方程中，建立了一种基于非线性光流方程的非迭代灰度梯度算法。

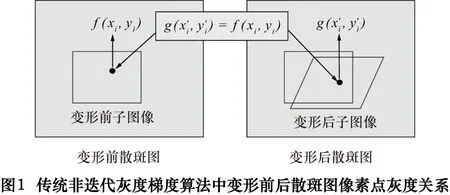
1 DIC的基本原理

数字图像相关方法通过处理由CCD/CMOS相机采集的被测物体表面加载前后的散斑图像而获得变形参数。相机在加载前采集的散斑图通常被称为参考图像，而加载后获得的散斑图称为变形图像。图2给出了数字图像相关方法的计算过程。首先以待求点P(xi,yi)为中心分别在参考图像和变形图像中取出两个方形区域，分别称为参考子图像和变形子图像，且变形子图像要比参考子图像大(如参考子图像取31×31，变形子图像取61×61)。然后将参考子图像与变形子图像按照某一预定相关函数进行互相关计算，得到相关系数分布曲面。相关系数曲面峰值点的位置与变形子图像中心点P的坐标差即为P点的位移矢量。对参考图像与变形图像中所有像素点进行上述操作，即可获得被测表面的全场位移。

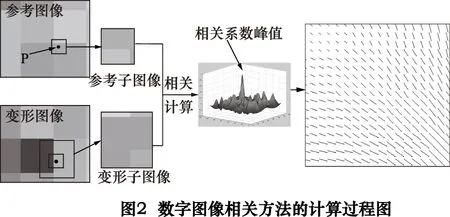
2 基于非线性光流方程的非迭代灰度梯度算法

考虑在实际应用中图像采集受到上述多种因素的影响，假设散斑图中任意一个像素点的灰度值在变形前后呈非线性关系，因此建立其非线性光流方程如下：

i=1,2,…,N

(1)

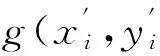
(2)

其中：u和v分别为参考子图像中心点沿x和y方向的整像素位移, Δx和Δy分别为参考子图像中心点沿x和y方向的亚像素位移。

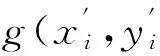
g(xi+u+Δx,yi+v+Δy)=

g(xi+u,yi+v)+Δxgx(xi+u,yi+v)+

Δygy(xi+u,yi+v)

(3)

因此，平方距离和(the sum of squared difference，SSD)相关系数可写为：

(4)

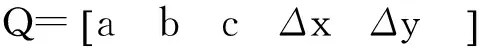
欲求S的最小值，应使函数取驻点值，因此有：

(5)

于是可得如下方程组：

(6)

其中:f=f(xi,yi)，g=g(xi+u,yi+v)，gx=gx(xi+u,yi+v),gy=gy(xi+u,yi+v)。

gx和gy为(x,y)点的一阶灰度梯度。

方程(6)可简写为：AQ=C，则方程的最小二乘封闭解为：

Q=(ATA)-1ATC

(7)

为了提高计算精度，本文采用双三次样条插值方法计算一阶灰度梯度，其表达式为：

(8)

插值区域大小为4×4像素。

3 实验验证

3.1 数值模拟实验

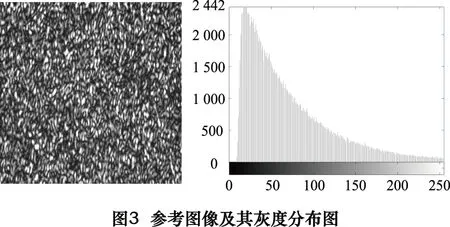
为了消除相机镜头畸变、离面位移等误差的影响，使算法的性能验证实验在可控的条件下进行。本文首先进行了数值模拟实验。图3为真实实验中采集的一幅大小为416×416像素的8-bit散斑图，将其作为本次实验中的参考图像。应用插值方法[10, 12]将该参考图像沿x方向平移-0.05像素。然后对平移后图像进行对比度和亮度的调整，模拟实际应用现场的环境变化及系统的偏差波动引起的散斑图灰度变化，进而得到7个灰度等级的变形图像。具体调整方法为[4]：

(1)将平移后散斑图的亮度依次增加20%，40%，60%，……，140%，从而获得7幅不同亮度的变形图像；

(2)将上述7幅变形图像的灰度值进行归一化处理后按照式(9)进行对比度拉伸处理，

Iout=

(9)

式中：Iin为输入的归一化后变形图像，Iout为对比度拉伸后输出图像；

(3)将对比度拉伸处理后的变形图像进行反归一化处理，从而获得7幅不同灰度变化等级的变形图像。图4给出了第7灰度等级的变形散斑图及其灰度分布，我们可以清晰地看出图像的灰度分布与原参考图像有着非常显著的变化。

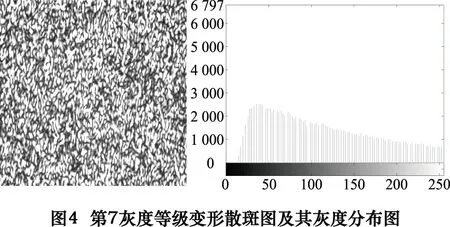
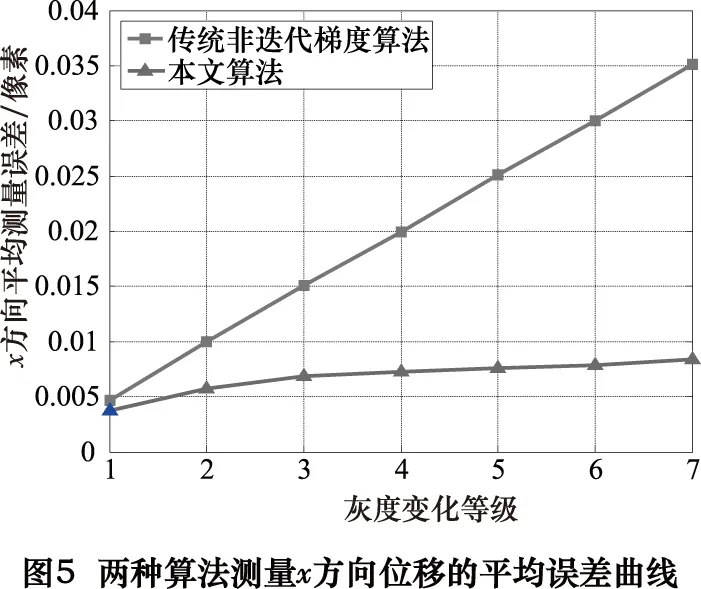
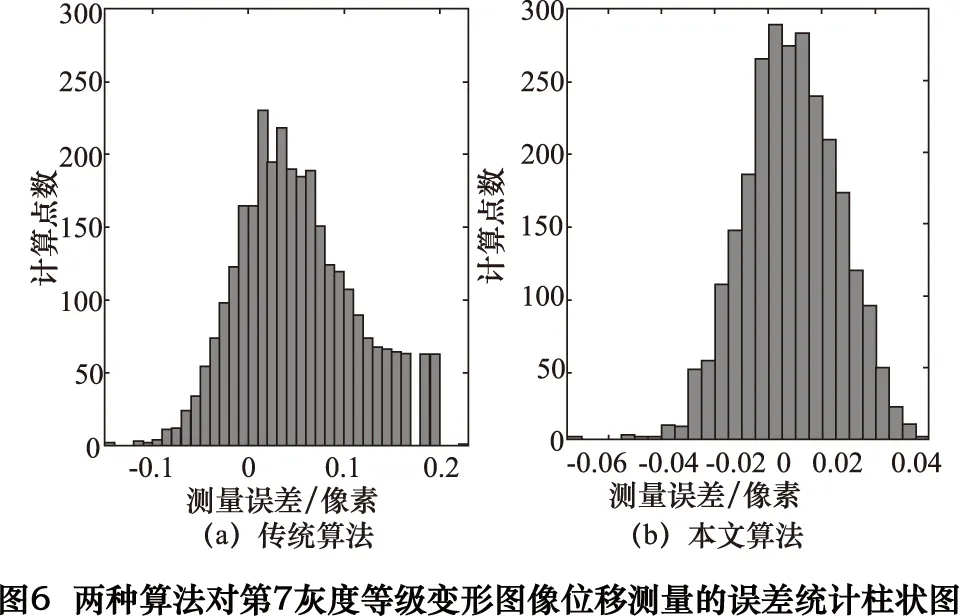
应用本文提出的改进灰度梯度算法和传统的非迭代灰度梯度算法对上述7幅变形图像的位移进行测量。测量计算时选取图像中2601(51×51)个均匀分布的计算点(计算点之间的距离为6个像素)。图5为两种非迭代灰度梯度算法测量x方向位移误差的平均值随灰度等级的变化曲线。从该曲线图中可以看出，随着灰度变化等级的增加传统算法的测量位移平均误差急剧增大，而本文算法的测量位移平均误差虽然也有增大的趋势，但变化非常缓慢且趋于平稳。在灰度变化最为显著的第7灰度等级变形图像测量中，传统算法的测量平均误差值已高达0.035像素，已超过真实位移(为0.05像素)的一半。而本文算法的测量平均误差此时仅为0.008 4像素，远小于传统算法的测量平均误差。这充分说明本文所提出的非迭代灰度梯度算法对光照变化、系统偏差波动等外界条件的变化不敏感，对上述影响因素给散斑图带来的灰度变化具有较强的鲁棒性。图6为两种算法测量第7灰度等级变形图像位移误差的统计柱状图。通过对比可以看出，虽然两种算法得到的测量误差统计柱状图形状上较相似(近似呈正态分布)，但不难看出本文算法的误差分布的主峰更突出且更靠近0点位置，测量误差的分散程度明显小于传统算法。这进一步说明本文算法在多种因素的影响下仍具有较高的测量精度(其他灰度等级变形图像的测量误差统计柱状图与第7灰度等级变形图像的测量结果类似，此处不再重复给出)。

3.2 拉伸实验

为了进一步评价本文算法的性能，进行了材料的拉伸试验。本实验所使用的试件为Q235哑铃型标准圆棒试件，通过人工喷洒黑白漆的方法在试件表面制作出均匀的散斑。制作的试件实物及其主要结构尺寸如图7所示。图8为本实验的拉伸测量系统，主要包括电子万能试验机(长春机械科学研究院生产)、两台平行安置的CCD相机(德国AVT公司生产，型号为Guppy PRO F-046B)、计算机、LED光源、引伸计等。两台CCD相机相当于引伸计的两个刃口，应用本文的DIC方法测量上下相机内中心区域变形，进而获得标距内轴向拉伸长度变化值。实验中安装引伸计的目的是为了用其测量数据与DIC测量数据进行对比，进而验证本文提出的DIC算法的性能。

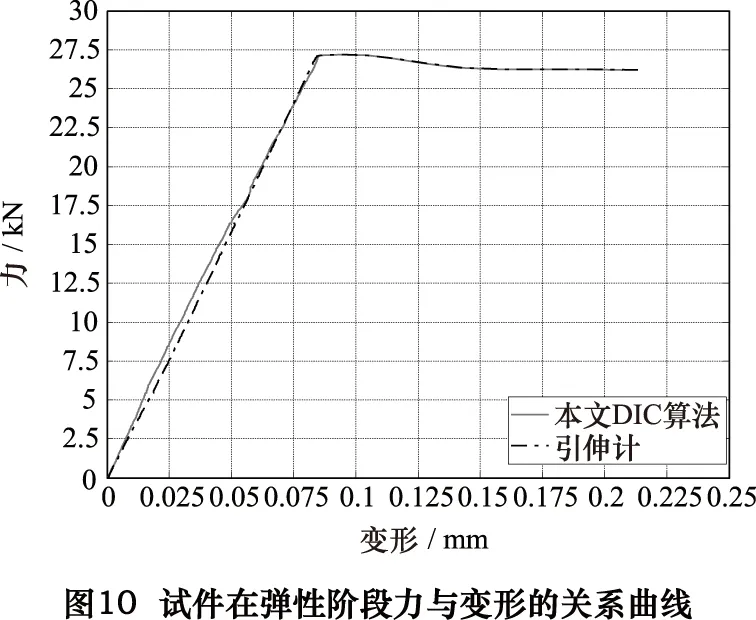
在拉伸实验之前，先进行像素当量的标定。将试验机的上夹头松开，以0.01 mm为步长连续移动试件5次，通过真实位移值与DIC的测量值(像素值)比值的平均值得到上下相机的像素当量分别为0.0212 mm/pixel和0.0213 mm/pixel。然后夹紧试件，启动试验机与图像采集系统，图9为上下相机采集的第一幅散斑图，并分别作为两台相机的参考图像。观察试验机的实时数据显示结果，当到达屈服阶段时，停止试验机及图像采集系统。图10为试件在弹性阶段引伸计与DIC法测得的力与变形关系曲线。从图中可以看出，两种方法获得的力与变形曲线非常吻合。DIC法和引伸计测得试件的弹性模量分别2.026 3和2.015，两者均在Q235弹性模量标准值2.00～2.10范围内。这进一步说明本文提出的非迭代灰度梯度DIC算法的可行性与有效性，并具有较好的测量精度。

4 结语

本文将非线性函数引入非迭代灰度梯度算法中，建立了基于非线性光流方程的非迭代灰度梯度算法。该算法无需迭代，直接获得亚像素位移的封闭解，易于实现。文中采用计算机模拟图像对传统非迭代梯度算法与本文算法在不同程度的图像灰度变化时求解精度进行了对比研究。结果表明，本文算法对图像灰度的变化具有较好的鲁棒性，在实验中求解灰度变化最大的第7灰度等级变形图像时传统算法的平均误差已达0.035像素，而本文算法仍然稳定在0.008 4像素以内。随后真实试件的拉伸实验进一步证明了本文算法的有效性并具有较高的测量精度。本文算法的研究也为非迭代灰度梯度DIC算法应用于复杂的现场环境条件下的变形测量奠定了基础。

[1]Pan Bing, Qian Kemao, Xie Huimin, et al.Two-dimensional digital image correlation for in-plane displacement and strain measurement: a review [J].Measurement Science & Technology，2009，20(6)：062001-17.

[2]戴相录，谢惠民，王怀喜.二维数字图像相关测量中离面位移引起的

误差分析[J].实验力学，2013，28(1)：10-19.

[3]Wang Min, Cen Yuwan, Hu Xiaofang, et al.A weighting window applied to the digital image correlation method [J].Optics & Laser Technology，2009，41(2)：154-158.

[4]刘小勇.数字图像相关方法及其在材料力学性能测试中的应用[D].长春：吉林大学，2012.

[5]Bruck HA，Mcneill SR，Sutton MA，et al.Digital image correlation using Newton-Raphson method of partial differential correction [J].Experimental Mechanics, 1989, 29(3)：261-267.

[6]王琛影, 何小元.相关识别中的曲面拟合法[J].实验力学, 2000, 15(9)：281-285.

[7]Davis CQ, Freeman DM.Statistics of subpixel registration algorithms based on spatiotemporal gradients or block matching [J].Optical Engineering, 1998, 37(4)，1290-1298.

[8]Zhou P, Goodson KE.Subpixel displacement and deformation gradient measurement using digital image/speckle correlation (DISC)[J].Optical Engineering, 2001, 40(8)，1613-1620.

[9]Pan Bing, Xie Huimin, Xu Boqin，et al.Performance of sub-pixel registration algorithms in digital Image correlation [J].Measurement Science & Technology，2006，17(6)：1615-1621.

[10]Xiong Lei, Liu Xiaoyong, Liu Guodong,et al.Evaluation of sub-pixel displacement measurement algorithms in digital image correlation [C].The International Conference on Mechatronic Science, Electric Engineering and Computer, 2011:1-4.

[11]潘兵, 续伯钦, 李克景.梯度算子选择对基于梯度的亚像素位移算法的影响[J].光学技术, 2005, 31(1)：26-31.

[12]Liu Xiaoyong, Li Rongli, Zhao Hongwei, et al.Quality assessment of speckle patterns for digital image correlation by Shannon entropy[J].Optik, 2015, 126(23): 4206-4211.

如果您想发表对本文的看法，请将文章编号填入读者意见调查表中的相应位置。

Non-iterative gray-gradient algorithm based on nonlinear optical flow equation in digital image correlation

LIU Xiaoyong, LI Rongli, HAO Zhaopeng, WANG Hui,CUI Gaojian, FAN Yihang, GONG Yan

(School of Mechatronic Engineering, Changchun University of Technology, Changchun 130012, CHN)

In traditional non-iterative gray-gradient algorithm of digital image correlation method, the gray intensity of a physical point on object surface is assumed that it does not change before and after deformation.However, in reality, the speckle images are sometimes acquired with illumination lighting variations, over/under-exposure, intensity variations during loading and so on.The gray intensity of physical points in speckle images before and after deformation is changed.In this paper, a non-iterative gray-gradient algorithm based on nonlinear optical flow equation is proposed.The nonlinear equation is employed to build the relationship between the points in the undeformed and deformed images.Both numeral experiment and real tensile experiment are conducted to verify the performance.The results show that the proposed algorithm displays the most robust for intensity variations and has high precision.

digital image correlation；nonlinear optical flow equation；non-iterative gray-gradient algorithm

* 国家自然科学基金项目( 51505038) ; 吉林省教育厅“十二五”科学技术研究项目( 吉教科合字[2015]第88 号)

0348

A

10.19287/j.cnki.1005-2402.2016.11.005

刘小勇，男，1979年出生, 博士，讲师，主要从事微纳米原位DIC测量技术与仪器方面的研究。

(编辑 谭弘颖)

2016-04-12)

161112