基于虚拟滑模控制方法的非合作航天器姿态估计

于晓婷，郁丰，何真，熊智，王振宇

（南京航空航天大学航天学院，江苏南京210016）

基于虚拟滑模控制方法的非合作航天器姿态估计

于晓婷，郁丰，何真，熊智，王振宇

（南京航空航天大学航天学院，江苏南京210016）

针对非合作航天器的非线性姿态估计问题，提出一种利用虚拟滑模控制思想实现对目标航天器姿态参数估计的方法。将立体视觉系统输出的实时观测数据作为虚拟控制系统的输入，将航天器的姿态动力学数学模型作为虚拟的控制对象，采用滑模变结构控制器计算出虚拟力矩控制量，从而使虚拟航天器的姿态与观测姿态同步，虚拟航天器姿态即为非合作航天器姿态参数的估计值。仿真实验验证表明，在存在系统误差及状态量初始误差较大的情况下，所提出的基于虚拟滑模控制的估计算法估计效果优于扩展卡尔曼滤波算法，并较好地协调了变结构控制鲁棒性与平滑控制抖振之间的矛盾。

控制科学与技术；立体视觉；非合作航天器；虚拟滑模控制；姿态估计；模糊边界层

0 引言

在轨运行的卫星由于燃料耗尽或姿态/轨道控制系统故障等因素，都有可能导致卫星失效成为太空垃圾。失效卫星一般是与追踪星之间没有直接信息交流的非合作目标卫星，非合作航天器之间的相对位姿测量是服务航天器开展非合作失效航天器的相对制导与控制的前提［1-2］，是对失效卫星进行在轨修复，燃料加注，捕获回收等在轨服务操作的基础。立体视觉系统因其低能耗、高性价比等优点已经成为测量相对位姿的常用三维传感器［3］。

对非合作航天器的姿态估计问题，描述航天器的姿态运动无论是采用欧拉角、罗德里格参数还是四元数，都具有非线性，在非线性滤波方法中，扩展卡尔曼滤波（EKF）由于方法简单、容易实现等优点而得到最广泛的应用［4-5］。无损卡尔曼滤波（UKF）也常被用于卫星姿态估计［6-8］，通过无损变换（UT）后的采样点集来逼近非线性函数概率分布，姿态估计结果较EKF具有更好的估计精度。但是以上两种滤波方法对模型精确性要求都较高，且在初始误差较大时，存在估计效果急剧下降和滤波器收敛速度缓慢的问题。H∞滤波作为一种鲁棒滤波器，对于有色噪声也具有较好的鲁棒性，而且它对不确定系统也具有很好的滤波效果［9］。以上滤波器在迭代过程中都需更新状态协方差矩阵，计算量较大，另外，协方差矩阵初值的选择会影响滤波器的初始收敛过程。粒子滤波（PF）是一种基于蒙特卡罗仿真的滤波方法，理论上只要粒子数目足够多，可以达到更好的收敛速度和估计精度［10-11］，然而随着粒子数目增多而导致计算量迅速增加，因此难以满足卫星姿态估计工程应用中对实时性的要求。

滑模控制（SMC）因其不依赖于外部扰动和内部参数的摄动，对系统的不确定性和建模误差具有较好的鲁棒性，是一种处理非线性控制问题的有效方法。由于故障卫星因为燃料消耗、帆板未完全展开等因素，惯量参数必然存在一定误差，本文针对模型存在系统误差等常规滤波方法估计效果不佳的情况，在滑模控制方法的基础上提出了一种虚拟控制的思想，将非合作卫星的姿态估计转换成控制问题，继承SMC的优势，在无需已知系统精确描述的情况下也可得到较好的估计精度，并且只需计算反馈力矩对系统模型进行调节，大大减少了计算量。

本文首先给出卫星动力学方程和四元数描述的运动学方程，将该模型作为虚拟控制的对象；然后利用立体视觉对特征点进行三维重构，得到目标星的姿态，将该姿态信息与估计姿态之差作为控制输入；采用Lyapunov方法设计了滑模变结构控制律来“控制”虚拟卫星的姿态与观测值同步。另外，SMC不连续开关特性会引起系统抖振［12-13］，在常规的准滑模变结构控制中引入模糊规则，利用模糊控制器来动态调整滑模边界层的厚度。最后仿真验证表明，该模糊滑模控制器有效地削弱了抖振，能较好地协调固定边界层变结构控制的鲁棒性与平滑控制抖振之间的矛盾；对比本文估计方法与EKF算法，在初始误差较大时本文方法依然具有较快的收敛速度，同时当对象存在系统误差时也能保证估计的鲁棒性，提高了姿态估计精度。

1 基于SMC方法的估计模型

1.1 基于虚拟SMC的状态估计模型

基于虚拟SMC思想的非合作航天器姿态估计的总体思路如图1所示。图1中qobv为立体视觉姿态测量值，qmol为基于模型的姿态预测值，M为控制力矩，ω为角速度。

图1 虚拟SMC系统结构图Fig.1 Block diagram of virtual sliding mode controller

本文估计器设计方法的基本思路是:将立体视觉的测量姿态作为控制目标，设计滑模姿态控制器，将姿态动力学模型作为一颗虚拟的数字卫星，控制该虚拟卫星的姿态与观测值同步。将卫星动力学方程以及由四元数描述的运动学方程，转化为由误差四元数和误差角速度描述的误差跟踪方程，以立体视觉测量的姿态与模型的估计姿态之差作为控制系统的输入，基于Lyapunov原理设计滑模变结构控制器，计算出虚拟控制力矩“作用”在姿态动力学模型上，以消除虚拟卫星姿态与测量姿态之间的偏差，最终达到虚拟卫星的姿态与观测姿态的跟踪同步。

1.2 卫星姿态动力学和运动学模型

故障卫星姿态动力学方程:

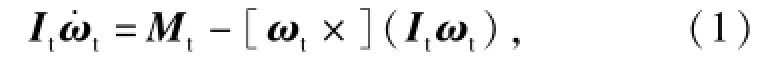
式中:ωt=［ωx，ωy，ωz］T为目标卫星相对于惯性空间的角速度在本体系中的分量；It为转动惯量；Mt为三轴控制力矩。对于坌ξ=［ξ1ξ2ξ3］∈R3，符号［ξ×］均表示:

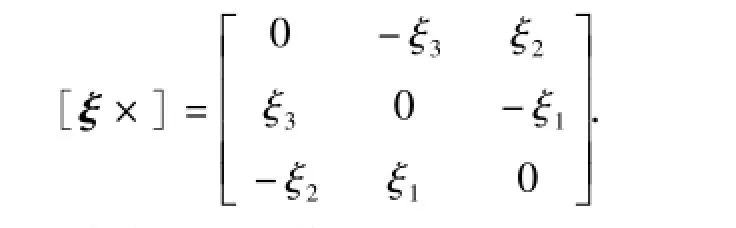
目标星姿态运动学模型:

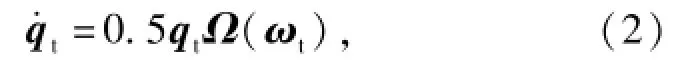
由（2）式可得姿态四元数的矢量和标量部分分别为

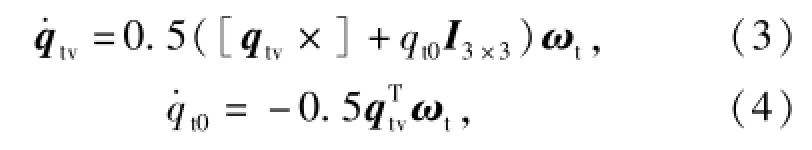
式中:qtv=［qt1，qt2，qt3］T是目标星姿态四元数的矢量部分；qt0为目标星姿态四元数的标量部分；I3×3为3×3的单位矩阵。

1.3 立体视觉的特征点三维重构

双目立体视觉三维测量是基于视差原理，如图2所示为典型的平行式双目立体视觉模型，两相机投影中心线的距离，即基线距为b，两相机在同一时刻观测空间中的同一特征点Pc（xci，yci，zci），在左右像面上的坐标分别为（uLi，vLi）、（uRi，vRi）.假定两相机的图像在同一平面上，则vLi=vRi；由于本模型要求两相机具有相同的内部参数，所以左右相机的焦距值相等，即f=fL=fR；追踪星质心与两相机中心之间的平移量为m，由几何关系可得

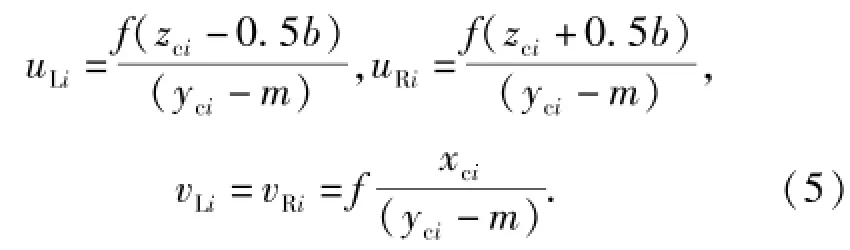
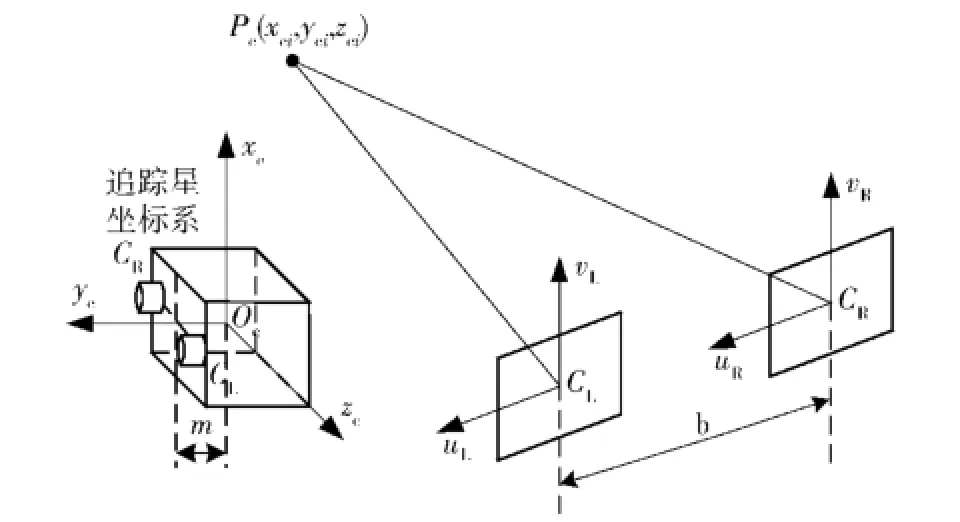
图2 双目立体视觉成像原理Fig.2 Imaging principle of binocular stereo vision

可确定特征点在追踪星本体系下的三维坐标为

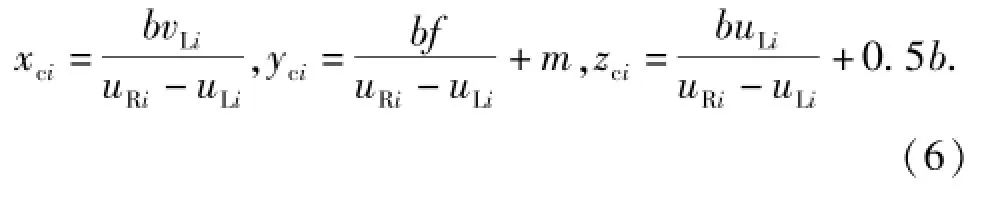
1.4 目标星的姿态测量

非合作目标一般与追踪星间无主动的信息交流，特征点也是卫星表面的自然特征，但是如果目标星是己方研制的，可以认为其结构和质量特性是已知的；如果卫星结构信息未知，可以通过目标在轨参数估计方法来估算质量特性、重建目标星的坐标系及特征点坐标［14-15］。特征点与目标星本体系Otxtytzt的空间关系如图3所示。

图3 特征点在两坐标系下的转换关系Fig.3 Transformational relation between two coordinate systems

如图3，假设目标卫星的特征点均分布在同一个平面内，以特征点s2为坐标原点，向量s2s1为z轴，以垂直于特征点平面且背离目标星质心的方向为x轴，建立特征点坐标系Osxsyszs，特征点在特征点坐标系与追踪星本体系间的转换关系为

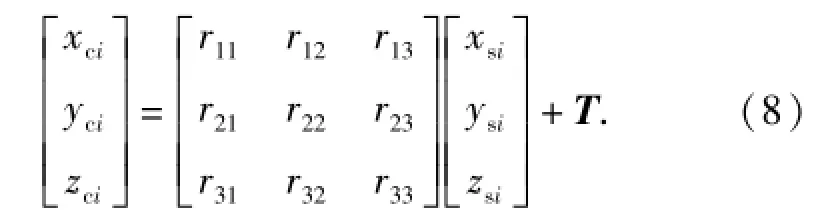
1）平移矩阵求解。s2在特征点坐标系中坐标为（0，0，0）T，在追踪星本体系的坐标为（xc2，yc2，zc2）T，代入（8）式中可得特征点坐标系Osxsyszs相对于追踪星本体系Ocxcyczc的平移矩阵T=（xc2，yc2，zc2）T.

2）转换矩阵求解。定义向量s2s1的方向为特征点坐标系的z轴，即特征点s1在z轴上，因此s1在特征点坐标系和追踪星本体系中的坐标分别为（0，0，zs1）T和（xc1，yc1，zc1）T，其中zs1=|s2s1|代入（8）式中，可解得转换矩阵的最后一列为

又因为特征点s3在特征点坐标系的Osxszs平面内，其坐标为（xs3，0，zs3）T，其中zs3为向量s2s3在z轴方向的分量，zs3=|s2s1·s2s3·s2s1/（|s2s1||s2s1|）|；xs3=|s2s3-s2s1·s2s3·s2s1/（|s2s1||s2s1|）|.在追踪星本体系的坐标为（xc3，yc3，zc3）T代入（8）式中可得

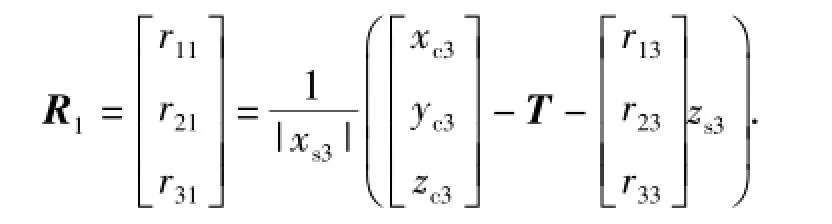
由R3和R1，可确定R2为

最后可得姿态转换矩阵R=［R1R2R3］，根据姿态转换矩阵可得四元数形式的目标星姿态量测值。

2 基于滑模变结构控制的姿态参数估计

根据目标卫星姿态误差模型来设计合适的滑模控制器，选择合适的切换函数和滑模控制律来改善滑模控制器的性能。利用模糊控制器来动态调整滑模边界层的厚度，改善滑模抖动的问题。控制结构图如图4所示。

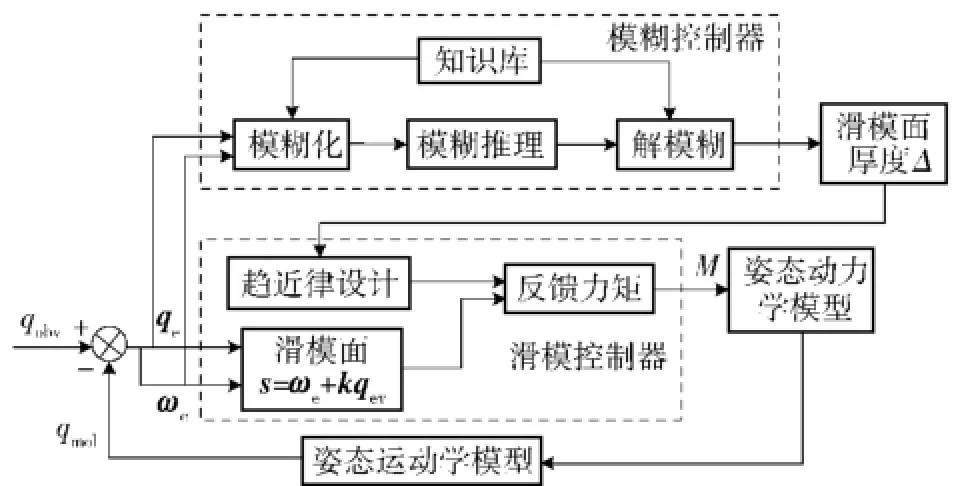
图4 虚拟滑模控制器系统结构图Fig.4 System structure of virtual sliding mode controller

2.1 姿态误差方程

医院医疗数据统计能够广泛收集各类病症的临床和诊疗数据，这些数据能够成为医师经验积累的有效依据，能够为今后的医疗服务工作提供有效的指导和参考，对于提升医疗服务水平具有重要意义。

将（10）式代入（3）式，得姿态误差微分方程为

式中:qev为qe的矢量部分；为ωt的标称值；ωe为目标星角速度的估计误差，

ωd为由观测数据推算的角速度，为目标卫星本体相对惯性系的角速度估计值，A（qe）为

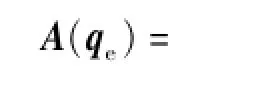
综合（1）式、（12）式，可得角速度误差模型为

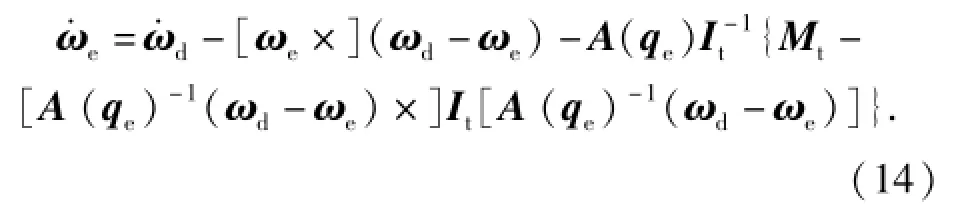
2.2 虚拟反馈控制力矩推导

定义切换函数为

式中:s=［s1，s2，s3］T；k=diag（k1，k2，k3），ki＞0.

系统运动点到达切换面附近时，当s→0+时，或当s→0-时，滑动模态发生，即当时满足滑模发生条件。

根据滑模可达性条件，状态空间任意位置运动点逼近切换面是一个渐进的过程，不能保证在有限时间内到达切换面。本文设计的指数趋近率包括指数项-Ks和等速趋近项-εsgn（s）以改善趋近运动的品质。本文选取指数趋近率:

对于由q和ω所描述的系统，分别设计三轴稳定航天器的姿态控制律，使系统在反馈控制量Mt= f（ω，q，s）的作用下实现:根据（14）式、（15）式与（16）式，SMC的反馈值为控制力矩:

2.3 滑模的防抖振设计

若采用常规的滑模趋近律如（16）式，SMC的不连续开关特性将会引起系统的抖振，用饱和函数sat（s/Δ）代替趋近律中的符号函数sgn（s），即

切换函数s是关于状态变量的函数，在2.2节中的滑模变结构控制方法中，由于边界层的厚度是不变的，但对于非线性系统来说，边界层厚度越小，控制效果越好，但同时又会使控制增益变大，抖振增强；反之，边界层厚度越大，抖振越小，但又会使控制增益变小，控制效果变差。考虑到模糊控制无需建立系统精确的数学模型，具有较强的鲁棒性，设计模糊控制器动态调整边界层厚度。

根据s的大小来实时调整边界层的厚度Δ，因s=ωe+kqev，模糊控制器的输入变量为qev和ωe，输出变量为滑模厚度Δ.上述3个变量取相同的论域为:｛-1.5，-1，-0.5，0，0.5，1，1.5｝，对应的模糊语言子集为｛NB（负大），NM（负中），NS（负小），ZO（零），PS（正小），PM（正中），PB（正大）｝，各模糊语言子集的隶属函数如图5所示。

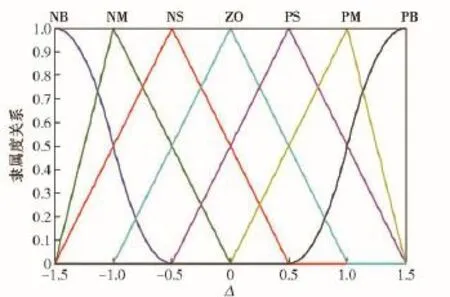
图5 边界层厚度隶属度关系图Fig.5 Boundary layer thickness membership

当s较大时，表示系统状态离滑模切换面比较远，应该用较宽的边界层厚度来避免抖振；当s较小时，表示系统状态离滑模切换面比较近，应该用较窄的边界层厚度来达到良好的控制精度。据此设计二维模糊控制器，模糊规则如表1所示。解模糊化方法采用重心法，图6为解模糊后生成模糊推理系统主接口（FIS）输出曲面，较直观地表现了输入变量与边界层厚度的关系。

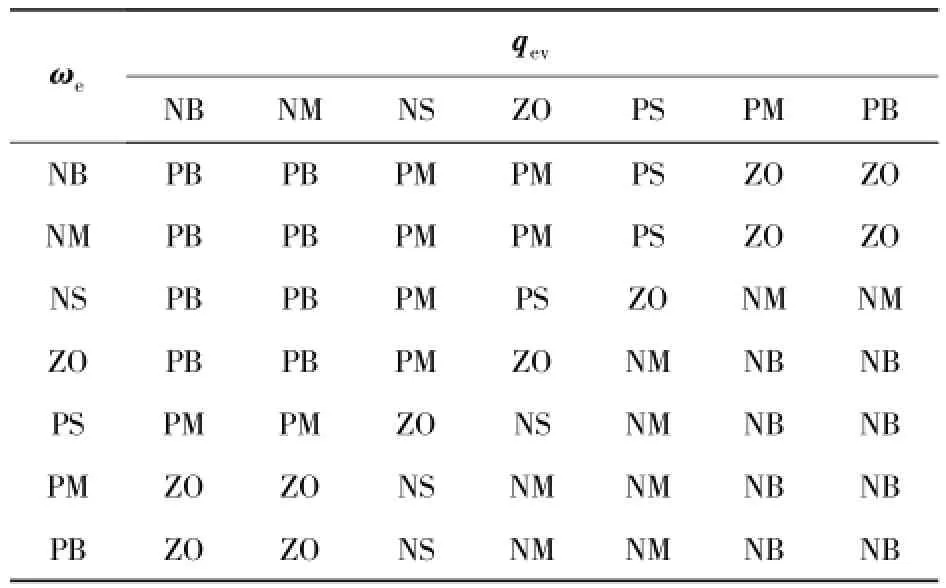
表1 模糊规则表Tab.1 Fuzzy rule table

图6 FIS输出曲面Fig.6 Output surface of FIS

2.4 稳定性证明

Lyapunov函数选取如下:

对（19）式进行求导，并将（18）式中经过饱和函数替换的趋近律代入（19）式中，得

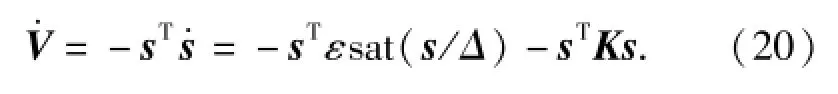
对于（20）式，总有V·＜0，故系统在状态变量处于滑动模态之外时是Lyapunov渐进稳定的，任何滑动模态之外的运动都最终要趋向于滑模面。

3 仿真与验证

因非合作卫星已经失去控制而在空间中做自由翻滚，由于帆板等挠性设备的阻尼作用，一般卫星最终将近似围绕一个定轴做旋转［16-17］。本文因此假设目标为自旋卫星，在短时间内可以假设其不受外力矩作用，转动惯量，初始角速度ωt=［0，-1，0］T°/s，初始四元数qt0=［1，0，0，0］T，角速度误差为ωe（0）=［0.1，0.5，0.2］T°/s.

相机参数:焦距为5 cm，两相机基线为0.8 cm，相机像素为1 600×1 200，像元大小为4.2 μm× 4.2 μm，像平面大小为6.72 mm×5.04 mm.

选择合适的切换函数和趋近律可以改善虚拟滑模控制器的性能，为探究虚拟滑模控制器中各参数对估计效果的影响，分析并归纳结论如下:

1）切换函数比例系数k.在定义切换函数s时，姿态四元数与角度之间的比值关系无法直接确定。从图7可较直观地看出:k越小，角度误差在切换函数的比重越小，曲线收敛速度越慢；反之，角度误差对切换函数的影响变大，通过虚拟反馈力矩对角度误差的校正也越及时，姿态角估计误差迅速收敛，但由于姿态四元数误差在s中权值较少，曲线收敛后抖动也随之变严重。

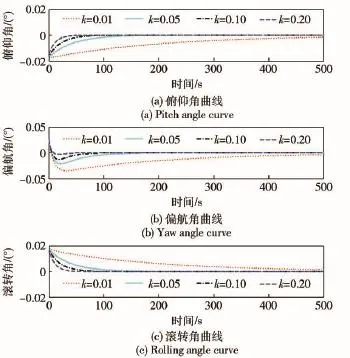
图7 切换函数比例项kFig.7 Proportion coefficient k of switching function

2）趋近律的指数项系数K.在趋近律中加入指数项-Ks是为了保证当s较大时，系统能以较大的速度趋近于滑动模态。如图8所示，随着K的增大，收敛速度明显变快，但同时伴随着剧烈的抖动。

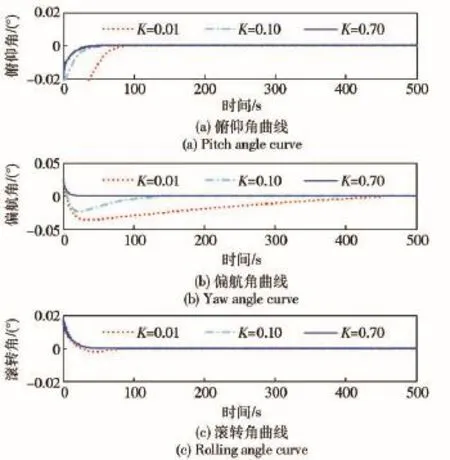
图8 趋近律的指数项系数KFig.8 Exponential coefficient K of reaching law

3）等速趋近项系数ε.ε表示系统的运动点在到达切换面s=0时的速率。图9为ε取值与估计效果的关系图。ε小，趋近速度慢；ε大，则运动点到达切换面时将具有较大的速度，引起的抖动也越大。

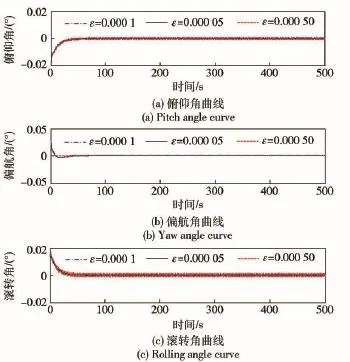
图9 等速趋近项系数εFig.9 Equal velocity reaching coefficient ε

综上所述，在指数趋近律中，为了保证快速趋近的同时削弱抖振，适当地增大K的同时减小ε，取K=0.7×diag（1，0.1，1），ε=10-5×diag（1，0.1，1），切换函数比例系数取k=0.05×diag（1，1，1）.

为验证模糊控制器抑制滑模抖振，提高估计精度的效果，分别对固定滑模边界层厚度和动态滑模边界层厚度两种情况下的切换函数s进行仿真，仿真结果如图10和图11所示。

原始的滑模控制器的边界层厚度不变，当s较大时，趋近律中的开关量sgn（s）使得当s接近于0时，趋近的速度是系数ε而非0，因此切换线一直处于抖动中。从图10可看出，x和z轴的抖动较大，25 s内的标准差分别为0.012 4和0.012 7；而根据切换函数s的大小动态调整边界层厚度后，如图11切换曲线的振动明显得到改善，x和z轴的标准差在25 s内分别降为0.003 2和0.004 8.因模糊控制器可根据s的大小来实时调整边界层厚度，当s较大时，表示系统的状态离滑模切换面比较远，应该用较宽的边界层厚度，这样比值s/Δ随之减小，可防止趋近速度=-εsat（s/Δ）过大，因此抖振得到缓解。

为验证状态量初始误差较大时两种方法的表现，设置滑模参数为k=0.05×diag（1，1，1），ε= 10-4×diag（1，0.1，1），K=0.1×diag（1，0.1，1）（以下仿真的滑模参数不变），状态初值误差取qe（0）=［1，（（7°，9°，-5°）π/180°）/2］T。图12和图13分别为两种方法对角速度和姿态角的估计误差。

图10 固定边界层厚度的切换函数sFig.10 Sliding surface switching curve of fixed boundary layer thickness

图11 模糊边界层厚度的切换函数sFig.11 Sliding surface switching curve of fuzzy boundary layer thickness

图12 初值误差较大时角速度误差估计Fig.12 Estimated error of angular velocity for lager initial state error

图13 初值误差较大时姿态角误差Fig.13 Estimated error of attilude angle for lager initial state error

无论是角速度还是姿态角，EKF需要更长的收敛时间，经分析EKF在存在状态初始误差的情况下，协方差阵初值的选择会对滤波器收敛效果产生直接影响；而由（17）式可知，虚拟滑模反馈力矩的大小是对角速度误差和姿态误差的直接反应，当初始姿态或角速度误差较大时，虚拟控制器会迅速向虚拟卫星反馈较大的控制力矩对角速度进行修正，同时姿态误差也会得到及时修正。图12中本文方法的角速度估计在虚拟反馈量的作用下能够迅速收敛，但噪声较EKF大，这是因为本文角速度输入值由角度差分得到，但是到1 000 s后也基本能够控制到与EKF相当的精度。

众所周知，SMC对系统的不确定性具有良好的鲁棒性，为验证本文将虚拟反馈思想引入滑模控制器中用于姿态估计后是否继承了SMC的优势，做如下仿真验证:因在工程实践中不可能得到精确的转动惯量值，例如故障卫星燃料经过消耗后而改变了质量特性，此处引入转动惯量误差Ite=，仿真结果如图14和图15所示。

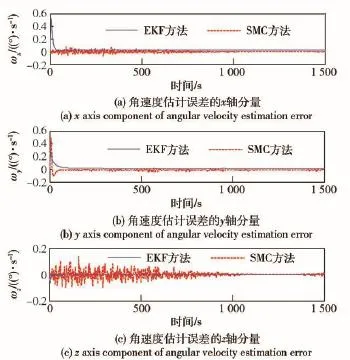
图14 系统误差下的角速度误差Fig.14 Estimated error of angular velocity in case of system error

由于EKF算法的精度严重依赖于模型的精度，无法对因惯量误差引起的角度与角速度误差进行更好的估计修正。图14为二者的角速度估计误差曲线，EKF算法的角速度并没有无偏收敛于0，而是相对0有约10-2的偏差；图15是二者的角度估计误差曲线，基于EKF方法的姿态角估计误差虽然总体收敛，但一直有波动，在同样的条件下，基于虚拟SMC方法的估计算法具有鲁棒性，对系统误差并不敏感，在虚拟反馈力矩的作用下对角速度和角度进行了调节，并在较短的时间内收敛。为对比两种方法的估计精度，取800～1 500 s时间内的姿态误差进行统计，如表2所示，收敛后EKF的姿态误差的标准差约为本文方法的3倍，本文方法的估计精度明显高于EKF的估计。

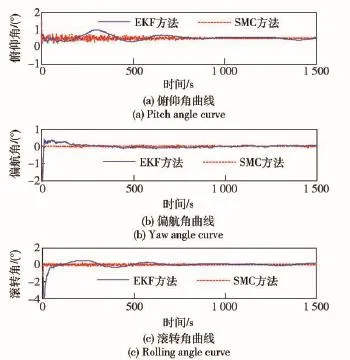
图15 系统误差下姿态角误差Fig.15 Estimated error of attitude angle in case of system error

4 结论

本文提出了一种利用虚拟SMC思想实现对非合作故障卫星姿态参数估计的方法，在状态量初始误差较大的情况下具有比EKF更快的收敛速度，在故障卫星转动惯量不准确而导致建模误差的情况下，比EKF算法取得了更好的估计精度。本文方法可以作为空间失效卫星交会对接过程中的目标姿态估计器设计的一种参考。

（References）

［1］ 梁斌，杜晓东，李成.空间机器人非合作航天器在轨服务研究进展［J］.机器人，2012，34（2）:242-256. LIANG Bin，DU Xiao-dong，LI Cheng.Advances in space roboton-orbit serving for non-cooperative spacecraft［J］.Robot，2012，34（2）:242-256.（in Chinese）

［2］ 崔乃刚，王平，郭继峰，等.空间在轨服务技术发展宗述［J］.宇航学报，2007，28（4）:805-811. CUI Nai-gang，WANG Ping，GUO Ji-feng，et al.The technology of on-orbit service development［J］.Journal of Astronautics，2007，28（4）:805-811.（in Chinese）

［3］ Segal S，Carmi A，Gurfil P.Stereo vision-based esti-mation of relative dynamics between non-cooperative satellites:theory and experiments［J］.IEEE Transac-tions on Control Systems Technology，2014，22（2）:568-684.

［4］ Son-Goo K，John L C，Yang C，et al.Kalman filtering for relative spacecraft attitude and position estimation［J］.Journal of Guidance Control and Dynamics，2007，30（1）:133-143.

［5］ 周军，白博，于晓川.一种非合作目标相对位置和姿态确定方法［J］.宇航学报，2011，32（3）:516-521. ZHOU Jun，BAI Bo，YU Xiao-chuan.A new method of relative position and attitude determination for non-cooperative target［J］. Journal of Astronautics，2011，32（3）:516-521.（in Chinese）

［6］ Crassidis J L，Markley F L.Unscented filtering for spacecraft attitude estimation［J］.Journal of Guidance，Control，and Dynamics，2003，26（4）:536-542.

［7］ Julier S J，Uhlmann J K.Unscented filtering and non-linear estimation［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，92（3）:401-422.

［8］ 陈记争，袁建平，方群.基于修正Rodrigues参数和UKF的姿态估计算法［J］.宇航学报，2008，29（5）:1622-1626. CHEN Ji-zheng，YUAN Jian-ping，FANG Qun.Atti-tude estimation using modified Rodrigues parameters and UKF［J］.Journal of Astronautics，2008，29（5）:1622-1626.（in Chinese）

［9］ 王新屏，张显库，张丽坤.H∞鲁棒滤波器与Kalman滤波器的对比研究［J］.系统工程与电子技术，2003，25（10）:1267-1269. WANG Xin-ping，ZHANG Xian-ku，ZHANG Li-kun.Comparison of H∞robust filter and Kalman filter［J］.Systems Engineering and Electronics，2003，25（10）:1267-1269.（in Chinese）

［10］ Cheng Y，Crassidis J L.Particle filtering for sequential spacecraft attitude estimation［C］∥AIAA Guidance，Navigation，and Control Conference and Exhibit.Providence.RI，US:AIAA，2004.

［11］ Oshman Y，Carmi A.Attitude estimation from vector observations using a genetic algorithm-embedded quaternion particle filter［J］. Journal of Guidance，Control，and Dynamics，2006，29（4）: 879-891.

［12］ 唐立力，罗丽娜，虞文斌.一种基于模糊边界层的转台伺服系统滑模控制器设计［J］.电气技术与自动化，2010，39（2）: 163-166. TANG Li-li，LUO Li-na，YU Wen-bin.Design of fuzzy sliding mode controller for flight simulator based on fuzzy boundary layer［J］.Electrical Technology and Automation，2010，39（2）: 163-166.（in Chinese）

［13］ Lhee C C，Park J S，Ahn H S，et al.Sliding mode-like fuzzy logic control with self-tuning the dead zone parameters［J］.IEEE Transactions on Fuzzy Systems，2001，9（2）:343-348.

［14］ Lichter M D，Dubowsky S.State，shape，and parame-ter estimation of space objects from range images［C］∥IEEE International Conference on Robotics and Automation.New Orleans，LA，US: IEEE，2004:2974-2979.

［15］ Yu F，He Z，Qiao B，et al.Stereo-vision based relative pose estimation for the rendezvous and docking of non-cooperative satellites［J］.Mathematical Problems in Engineering.2014，2014: 1:12.

［16］ 徐福祥.“风云一号”B卫星姿态控制系统［J］.中国空间科学技术，1997（6）:1-8. XU Fu-xiang.Attitude control system of FY-1B satel-lite［J］. Chinese Space Science and Technology，1997（6）:1-8.（in Chinese）

［17］ 周鼎.基于立体视觉的非合作航天器相对状态估计［D］.哈尔滨:哈尔滨工业大学，2015. ZHOU Ding.Estimation of relative state between non-cooperative spacecraft based on stereo vision［D］.Harbin:Harbin Institute of Technology，2015.（in Chinese）

Virtual Sliding Mode Control-based Attitude Estimation for Non-cooperative Spacecraft

YU Xiao-ting，YU Feng，HE Zhen，XIONG Zhi，WANG Zhen-yu
（College of Astronautics，Nanjing University of Aeronautics and Astronautics，Nanjing 210016，Jiangsu，China）

A virtual sliding mode control design method is proposed for the nonlinear attitude estimation of non-cooperative spacecraft.The real-time observations outputted by the stereo vision system are used as the inputs of the virtual sliding mode controller，and the spacecraft attitude dynamics mathematical model is taken as a control object of the virtual controller.The virtual control torque is calculated by using the sliding mode variable structure controller.The virtual spacecraft attitude and the observed attitude are synchronous，and the virtual spacecraft attitude is the estimated value of attitude parameter of the non-cooperative spacecraft.Simulation result shows that the proposed estimation algorithm based on virtual sliding mode controller performs better than the extended Kalman filtering algorithm.The application of sliding mode boundary layer control achieves a good balance between the robustness of variable structure control and the smooth control chattering.

control science and technology；stereo vision；non-cooperative satellite；virtual sliding mode；attitude estimation；fuzzy boundary layer

V448.21

A

1000-1093（2016）07-1282-09

10.3969/j.issn.1000-1093.2016.07.017

2015-06-30

国家自然科学基金项目（61203197）；中国航天科技集团公司航天科技创新基金项目（2014年）

于晓婷（1990—），女，硕士研究生。E-mail:yxting90@163.com；

郁丰（1980—），男，副研究员，硕士生导师，博士。E-mail:yufeng@nuaa.edu.cn