图最小线性排序问题的Memetic爬山算法*

陈雄峰，陈 振，徐 戈

1.闽江学院 计算机科学系，福州 350121

2.福建省信息处理与智能控制重点实验室，福州 350121

3.福州大学 离散数学与理论计算机科学研究中心，福州 350108

图最小线性排序问题的Memetic爬山算法*

陈雄峰1,2+，陈 振3，徐 戈1,2

1.闽江学院 计算机科学系，福州 350121

2.福建省信息处理与智能控制重点实验室，福州 350121

3.福州大学 离散数学与理论计算机科学研究中心，福州 350108

CHEN Xiongfeng,CHEN Zhen,XU Ge.Memetic hill climbing algorithm for minimum linear arrangement problem.Journal of Frontiers of Computer Science and Technology,2016,10(11):1623-1632.

针对图最小线性排序问题优化目标的特性及其可行域总是连通的特点，提出了一个新型的Memetic爬山算法。在Memetic算法框架及其主要算子内部流程中同时结合爬山法，并在主要算子内部采用迂回爬山策略。设计可变型顶点-边-邻接交叉算子，改进使用基于贪心随机自适应搜索过程的初始解生成算法，采用动态更新等保持种群多样性策略。公认测试集的实验结果表明，与最近的两阶段模拟退火算法（two-stage simulated annealing，TSSA）和分散搜索与路径重链接算法（scatter search and path relinking，SSPR）相比，该算法具有更好的整体性能。在相近平均运行时间内，该算法近优解质量分别平均提高1.6%和2.01%，21个测试例子中13个获得当时最好的近优解，比TSSA算法多出4个，比SSPR算法多出2个。

最小线性排序；Memetic算法；爬山法；邻接交叉

1 引言

图最小线性排序（minimum linear arrangement，MinLA）问题是对无向图顶点进行线性排序，寻找使得边长总和最小的顶点线性排序，其中边长定义为边的两个顶点在序列位置之间的距离。自1964年Harper为设计纠错码而首次提出以来，MinLA已广泛应用于VLSI（very large scale integration）设计、自然语言处理、图形绘制和并行与分布式处理等许多领域[1-3]。针对一些诸如树、超立方体等特殊图，MinLA有多项式时间的确定性算法，而针对一般图，MinLA属于NP难组合优化问题，需用启发式算法在合理的运行时间内求得近优解[1-2]。

迄今为止主要的MinLA问题启发式算法有谱序列、混合模拟退火、混合遗传（包括Memetic）、多层加权边缩减和分散搜索与路径重链接（scatter search and path relinking，SSPR）等算法[1-7]。这些算法的基本思想包括：（1）采用适当的启发式引导算法将有边连接的顶点彼此靠近，以求得高质量的近优解；（2）使用相对高质量的初始解和可调节问题解多样性与同质性的目标函数等措施以优化搜索区域；（3）设计高效的邻域函数或局部搜索、交叉等主要算子以提高搜索效率，减少运行时间[2,7]。对公认的测试集[8]实验结果表明，结合谱序列算法生成初始解和模拟退火算法搜寻高质量问题解的优势，可同时改进各自原来算法的运行时间和近优解质量[2,6]。文献[4]的遗传爬山混合算法虽然结合谱序列算法生成初始解、交叉和爬山法的优势，但采用通用型的两点交叉算子，与之前的算法相比，仅可对少数测试例子获得更好的近优解和运行时间[2,4-5]。文献[5]的Memetic算法设计了具有问题针对性的交叉算子，使用基于模拟退火算法的局部搜索，可对大部分测试例子获得好于遗传爬山混合算法的近优解。上述3种算法因为分别受制于模拟退火算法或通用性交叉算子的搜索效率，运行时间都相对较长。文献[6]的两阶段模拟退火（two-stage simulated annealing，TSSA）算法集成了相对高质量初始解生成方法、可调节问题解多样性与同质性的目标函数和针对性的邻域函数，对大部分测试例子可获得当时最好的近优解，与之前算法相比，运行时间也大幅减少。文献[7]的SSPR算法使用与TSSA算法[6]相似的初始解生成方法，与Memetic类似基于种群的算法框架，以分散搜索为局部搜索，以路径重链接进行全局探测。与TSSA算法相比，在相近的平均运行时间内，SSPR算法可对更多测试例子获得当时最好的近优解。

Memetic算法结合了遗传或其他进化算法和局部搜索，在利用交叉算子全局探测优势的基础上，通过结合局部搜索过程增强搜索性，全局探测与局部搜索性能相对均衡，因而被成功地应用于处理许多组合优化问题[5,9-18]。Memetic算法的缺点是时间和空间复杂度较大。本文基于MinLA问题优化目标的特性，研究选用适当的启发式方法进行针对性设计，提出了一个新型的MinLA问题Memetic爬山混合算法。在公认的测试集[8]上进行实验，结果表明了这些设计策略的有效性。与TSSA和SSPR算法相比，本文算法在相近的平均运行时间内，对大部分测试例子可有效提高问题近优解的质量，并对更多测试例子可获得当前最好的近优解。

2 问题表示与目标函数特性

给定无向图G=(V,E)，其中V(|V|=n)为顶点集合，E(|E|=m)为边集合。图G顶点的一个线性排序φ视为顶点与位置标号1,2,…,n之间的一一对应函数，即φ：V→{1,2,…,n}。在图G顶点为线性排序φ的情况下，顶点v(v∈V)的位置标号记为φ(v)，则边(u,v)∈E的长度为|φ(u)-φ(v)|，图G总边长记为LA(G,φ)，定义如式（1）：

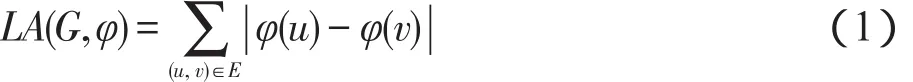
LA(G,φ)还可视为所有“顶点v与其全部邻接点N (v)之间边长之和L(v,φ)”的累加。L(v,φ)定义如式（2），则LA(G,φ)可表示如式（3）：

MinLA问题就是寻找图G顶点的一个线性排序φ*，使得LA(G,φ)最小。

Memetic算法染色体编码可直接使用顶点线性排序的形式，优化目标函数可直接使用LA(G,φ)。基于优化目标函数LA(G,φ)具有式（1）、（3）累加项的特性，将“顶点及其任意个邻接点”作为Memetic算法的交叉基因片段，对后代个体继承或重组“邻接顶点之间彼此靠近”的优良基因片段，减小目标函数值，具有更好的启发效果，因而对算法交叉操作所隐含的全局探测过程具有更为有效的引导性。并且可通过灵活限定其中邻接点个数，如当其中邻接点个数限定为1时，就是将“边”作为交叉基因片段，以适应不同类型图的特点，从而可对更多类型的图提高近优解的质量。

3 算法设计

3.1 算法框架

MinLA问题Memetic爬山（Memetic hill climbing，MHC）混合算法为交叉、局部搜索结合爬山法的算法，基本框架如算法1所述。

算法1 MinLA问题Memetic爬山算法

就基于种群的进化算法而言，种群规模在一定范围（约100个）以内，扩大种群规模会明显提高进化效率[9]。另一方面，面对较大规模问题时，因其空间复杂度较高，受运行环境制约，通常不得不采用较小规模（30个及以下）种群。算法框架中采用双向交叉策略，相当于单向交叉并使用两倍于现有规模的种群，但只需大约其1/2的内存空间和参数传递次数，可明显提高算法处理较大规模问题时的进化效率。实验表明，与单向交叉并直接使用两倍于现有规模的种群相比，当问题规模较小而可使用20～30个体种群时，可节省运行时间约8%～22%；当问题规模较大而不得不使用5～10个体种群时，可节省运行时间约45%～87%。适当的种群多样性对提高启发式算法的近优解质量和进化效率都有直接的作用[9,13-14]。算法采用动态更新种群为保持多样性的主要策略，采用3.2节初始种群生成策略为平衡多样性与同质性的主要策略，每一代重新随机排列种群个体为次要策略。更新种群时，保留1～2个当前最好的个体，其他个体替换为新的初始个体。另外，实验表明使用爬山法时，接受顶点排序有变化而LA(G,φ)不变即“=”的个体为后代个体，非常有利于进一步的搜索。算法1中初始种群生成、交叉算子、局部搜索、变异算子将分别在后面3.2～3.5节详细介绍。

3.2 初始种群生成

初始解的质量决定了初始搜索区域的优劣，是影响启发式算法整体性能的关键因素之一[6,9]。综合考虑生成初始解的质量和计算时间，经过比较分析，初始解个体生成算法选用文献[6-7]基于连接程度的启发式“sf(v)=dU(v)-dL(v)”和基于对目标函数影响程度的启发式“,w∈N(v)∩L,φ(v)=l” 。其中，v为待标号的顶点；U为未标号顶点集合；L为已标号顶点集合；dU(v)为U中与v邻接的顶点数；dL(v)为L中与v邻接的顶点数；N(v)为v的全部邻接顶点集合。构造过程使用贪心随机自适应搜索过程（greedy randomized adaptive search procedure，GRASP）[6-7,9]。

初始解个体生成算法具体流程如算法2所述。其中，在直接影响初始解个体特征的3个关键点都加入限制候选集RCLfirstu、RCLsf和RCLCv。加入RCLfirstu以排除少数度远大于平均度的顶点作为线性序列的第一个顶点，引导算法将其放置在线性序列的中部，更利于减小目标函数。加入RCLsf和RCLCv目的都是针对顶点度分布相对均匀的图，以便于在不降低同质性的前提下增强其初始解的多样性，其中RCLCv显然具有更为直接的影响。通过调整各限制候选集的阈值，不仅可针对不同类型的图生成良好的初始解，也可对同一类型的图生成不同特征的初始解，以保证初始解在特征上具有适当的多样性与同质性。设置各限制候选集的阈值时，可通过简单实验观察确定可获得较好初始解的一个阈值范围，而后随机使用该范围的阈值。实验观察同一类型图可设定大致相同的阈值范围。要进一步提高算法的鲁棒性，可让阈值范围自适应于图内部的邻接关系，如图顶点度的分布特征等。

算法2初始解个体生成算法

而后组成初始种群时，在若干（如2～5 000个）候选初始解个体中选择最好的作为一个种群个体，不同种群个体可设定有不同的候选个数，以使初始种群在质量上也具有适当的多样性。实验观察，针对较大规模的图，种群中含有10%～20%高质量的个体，非常利于获得良好的搜索区域，从而提高算法性能。

3.3 交叉算子

交叉算子的性能是影响Memetic算法整体性能的主要因素，要使得算法获得高质量的近优解，通常需针对问题的具体特性，设计高性能的交叉算子[5,9-17]。本文基于优化目标函数LA(G,φ)式（1）、（3）累加项的特性，将“顶点及其任意个邻接点”作为交叉基因片段，结合爬山法，并采用文献[18]FM算法迂回爬山策略，设计了可变型的顶点-边-邻接交叉算子(vertexedge-adjacent crossover，VEAX)。VEAX可通过限定“顶点及其任意个邻接点”中的邻接点个数，实现不同类型的交叉。当邻接点个数限定为0时即为“顶点交叉”，邻接点个数限定为1时即为“边交叉”，邻接点个数大于1的交叉简称“邻接交叉”。交叉类型可通过简单实验确定，以适应不同类型图的特点，如4.2节实验确定其中两种类型的图采用“边交叉”，其他4种类型的图采用“邻接交叉”。

图1所示为“邻接交叉”。pf、pm上将进行“顶点2及其邻接点1、3”的交叉，pm上7、9、0为分别与pf上2、1、3对应位置的顶点。采用与PR[7]和通用型的部分匹配交叉算子（partially-matched crossover，PMX）相同的交换机制。交叉过程可简化为直接在pm上进行顶点交换，如图1双箭头虚线所示。因此，cm可视为由pm进化而来，在pm的基础上，不仅可快速计算cm的目标函数值，而且可结合爬山法进行高效率的后代选择。

Fig.1 VEAX diagram图1 VEAX示意图

VEAX算法流程如算法3所述。其中，交叉过程采用与文献[18]FM算法类似的迂回爬山策略，接受可使得目标函数值最小的“某一对及其之前的全部顶点交换”。这一策略可使得算法比较容易跳出局部优解的区域，从而大大提高搜索效率[14,18]。逐对交叉顶点时，首先交叉被选择的顶点u与其对应顶点，可更好引导子个体继承或重组优良的“顶点u及其邻接点”部分排序。另外，实验观察交叉过程也可能出现多次达到目标函数值最小的现象，算法3通过加入限制候选集，以优化可接受交换顶点对数的范围，随机接受其中的某一次，可更好地适应不同规模问题解空间的特点。

算法3顶点-边-邻接交叉算子VEAX算法

输入：图G(V,E),父个体pf,母个体pm,一次交叉“顶点及其任意个邻接点”个数cross_VEAnumber，一个“顶点及其任意个邻接点”中邻接点限定最大个数VEA_adjnumber，交叉过程中有多次目标函数值达到最小情况下可接受交换顶点对数阈值比例accept_α

算法3中VEA_adjnumber取值决定交叉类型，如本节第一段所述可首先通过简单实验确定。而后为使算法在获得高质量的问题解与避免陷入局部优解之间达到良好的平衡，可进行详细实验确定cross_VEAnumber。一次交叉过程交换顶点对的最大数为s-1=VEA_adjnumber×cross_VEAnumber，可视为交叉所隐含的全局搜索的步长上界。针对相对高质量的种群，应采用交叉局部化的思想才能有较高的搜索效率[9,13]。如4.2节实验，VEA_adjnumber限定小于16；当母个体pm为当前最好个体时，cross_VEA number限定取值1～4，当母个体pm为非当前最好个体时，cross_VEAnumber设定为当前最好个体的1.5～2.5倍，随着当前最好个体质量的进化提高而逐步加大倍数。这一cross_VEAnumber取值方案可使得更新种群后非当前最好个体加快进化，尽快接近当前最好个体，进而可交叉生成更好的后代个体。accept_α的取值将确定全局搜索步长的下界，适当取值可进一步优化步长的范围。相对较小规模问题（如边数< 500）交叉时容易陷入局部优解，accept_α应设定为接近0，使步长接近上界，而相对较大规模问题交叉时容易错过高质量的问题解，accept_α应设定为接近1.0，使算法可进行较小步长的全局搜索，具体参见第4章“实验结果与分析”相关内容。

基于交叉局部化，如上所述VEAX交叉最大顶点对数s-1为常数。VEAX中使用集合L存放交叉过程的顶点对及当前目标函数值，使得c0,c1,…,cs-1可共用一个大小为|V|的存储空间，大大节省了存储空间。VEAX基本操作为顶点交叉和计算L(w,ck)(w∈V，0≤k≤s-1)，交叉最大顶点数为常数(s-1)×2，L(w,ck)平均时间复杂度为O(Ave(|N(w)|))，因此VEAX平均时间复杂度也仅为O(Ave(|N(w)|))。通常Ave(|N(w)|)远小于|V|，VEAX具有快速高效的性能。

3.4 局部搜索

MinLA问题解为一维线性排序，顶点位置变化直接影响目标函数值。依据这一特征，算法的局部搜索选用窗口穷尽搜索策略。每次局部搜索随机选择若干个窗口，实验观察每个窗口设定为4个连续顶点效果最好，在窗口内进行穷尽搜索，获取窗口内最好顶点排序。局部搜索概率PLS和每次局部搜索窗口个数的设定，应考虑与全局搜索即交叉之间的平衡，同时兼顾运行时间。经过实验，算法中PLS的取值范围随着当前最好个体质量的进化提高而逐步扩大，从2%～12%逐步扩大到2%～100%，在某一取值范围内个体质量越高，PLS取值越大。每次进行局部搜索的窗口个数约为每次交叉最大顶点对数的0.5～3.0倍，通常情况下图越稀疏倍数应越大，以协调局部搜索和全局搜索。此外，与3.3节“交叉算子”中cross_VEAnumber设定同理，种群中非当前最好个体的窗口个数设定为当前最好个体的两倍。

3.5 变异算子

将染色体上连续部分作为交叉基因片段时，如单/双点交叉和PMX等，通常采用交换染色体任意两个位置的编码作为变异策略，以弥补其交叉时全局探测性能的局限。本文交叉算子采用非连续的交叉基因片段和交换策略，需要弥补交叉时局部搜索性能的局限，因此选用有邻接的几个顶点往其中位数位置聚集成为一个连续部分的变异策略。聚集过程类似于文献[6]的邻域函数和文献[16]的局部搜索，但聚集后的前后顺序不一定是聚集前的顺序，而是重新随机排列以增强变异的效果。算法流程类似3.3节VEAX，也结合了迂回爬山策略，随机接受目标函数值LA(G,φ)没有变大即“≤”的“某一步及其之前的全部聚集”所带来的变异。实验观察，一次变异的有邻接顶点个数设定为1～5个（实际影响2～10个）效果最好。这一变异策略对较小规模的图和高质量初始解，提高问题近优解质量的作用尤为明显。变异概率PMU设定策略与3.4节“局部搜索”中PLS相同，取值约为PLS的15%，即0.3%～15%。

3.6 算法可行性分析

Memetic算法虽然被广泛应用于处理许多组合优化问题[5,9-17]，但其缺点是必须进行大量的适应值估算，具有较大的时间和空间复杂度。问题针对性设计利用问题领域先验知识增强算法的整体性能，是改进Memetic算法性能的主要措施之一，主要包括问题解表示、初始解生成和搜索算子设计三方面[9,13]。针对性问题解表示和初始解生成的目的是提高算法搜索区域的质量，针对性搜索算子设计是为了使搜索过程更为适合问题的特点及其解空间的适应值地貌特征，增强其搜索求解的效率。

本文基于MinLA问题优化目标的特性，研究选用适当的启发式，针对性设计一个MinLA问题Memetic爬山混合算法。首先改进使用文献[6-7]初始解生成方法以提高初始搜索区域的质量。而后针对MinLA问题可行域总是连通的特点，利用爬山法在连通可行域上搜索效率高的优势[4,9,13,16-17]，在算法框架的后代个体选择和交叉、变异和局部搜索主要算子内部邻域个体选择时都结合了爬山法，以提高算法的搜索效率。此外，为使算法更易于跳出局部优解区域，针对其交叉、变异算子内部搜索过程中会出现“问题解质量多次下降后再爬升”的现象，采用文献[18]著名的FM划分算法的爬山接受策略，即接受逐对交换顶点过程获得最好爬升的“某一对及其之前可能出现下降的全部顶点交换”，这里称之为迂回爬山策略。对公认的测试集实验结果表明了这些设计策略是有效的。

4 实验结果与分析

算法使用C++语言实现，测试运行环境为Windows XP，Pentium®dual-core CPU 3.2 GHz，RAM 2.0 GB。使用文献[8]提出的公认测试集，包括均匀随机（uniform random）、几何随机（geometric random）、已知最优解（包括树、超立方和网格）、有限元离散化（finite element discretizations）、VLSI设计（VLSI design）和图绘制竞赛（graph-drawing competition）6种类型的图。种群规模Np依据图的边数确定，具体为：（1）边数<500，Np=30；（2）500≤边数<1 500，Np=20；（3）1 500≤边数<10 000，Np=10；（4）边数≥10 000，Np=5。交叉类型（顶点或边或邻接）、accept_α和一次连续交叉“顶点或边或邻接”个数cross_VEAnumber依据图类型实验确定，分别设定为近优解LA(G,φ)最小的取值。交叉概率为1.0，变异、局部搜索概率等其他取值如上文相关章节所述。Nu取300，即当前最好个体300代没有进化就更新种群，“算法终止条件”设定为“3 000代当前最好个体LA(G,φ)进化减小量≤当前最好个体LA(G,φ)×10-6”。

4.1 算法性能

算法整体性能以获得的近优解平均LA(G,φ)和平均运行时间来衡量。在平均运行时间均控制在1 000 s内的情况下，与最近的整体性能最好的两个算法TSSA[6]和SSPR[7]与其他典型算法GH[4]、DTSA[19]、SSSA[20]、AMG[21]进行比较。实验结果如表1所示，其中“其他典型算法”为上述4种算法最好的平均LA(G, φ)；“TSSA”和“SSPR”分别为两种算法所获得多个近优解的平均LA(G,φ)[7]；“本文算法MHC”为在控制与文献[7]相近平均运行时间的情况下，所获得10个不同近优解的平均LA(G,φ)；“比其他改进”、“比TSSA改进”、“比SSPR改进”分别是“本文算法MHC”较之三者的减小百分比。

文献[7]测试运行环境同样是CPU 3.2 GHz，RAM 2.0 GB，因此可以认为本文算法MHC的运行时间介于SSPR和TSSA算法之间。与TSSA和其他典型算法相比，基于种群的本文算法MHC和SSPR具有更好的全局探测性能，因而可对更多类型的测试例子获得高质量的近优解，特别是对较为稠密的测试例子尤为明显。本文算法MHC与SSPR相比，具有更好的启发式，因而可大幅提高绝大部分测试例子近优解的质量，其中少数测试例子的近优解质量低于SSPR，主要原因是种群多样性控制策略还不够精细。对测试例子gd96a，本文算法MHC和SSPR近优解质量都大幅低于TSSA，主要原因是未能获得良好的初始解。

4.2 交叉算子VEAX收敛性

为进一步验证顶点-边-邻接交叉算子VEAX（算法3）的有效性，以及VEA_adjnumber（交叉类型）、accept_α取值的合理性，分别对测试集的所有例子进行收敛性测试。测试时除了要测试的参数，其他参数和运行时间与4.1节保持一致。VEA_adjnumber取值0、1和大于1分别表示“顶点交叉”、“边交叉”和“邻接交叉”，由于需要控制运行时间和基于交叉局部化的思想，其中平均邻接点个数大于16的测试例子VEA_adjnumber=16，其他的不限。accept_α分别取值0.1，0.2，…，1.0。所有测试结果表明，除了“图绘制竞赛”略有不同，同一类型测试例子的最好交叉类型accept_α取值相同。限于篇幅，仅列举不同类型图的代表性例子和accept_α分别取值0、0.5、1.0的测试结果，如表2、表3所示，其中数值为所获得10个不同近优解的平均LA(G,φ)。一次交叉连续“顶点-边-邻接”个数cross_VEAnumber采用类似方法实验确定，表2中“一次交叉个数”直接列出其最好取值范围。

Table 1 Test results of MHC algorithm and comparison of typical heuristic algorithms表1 MHC算法测试结果及典型启发式算法比较

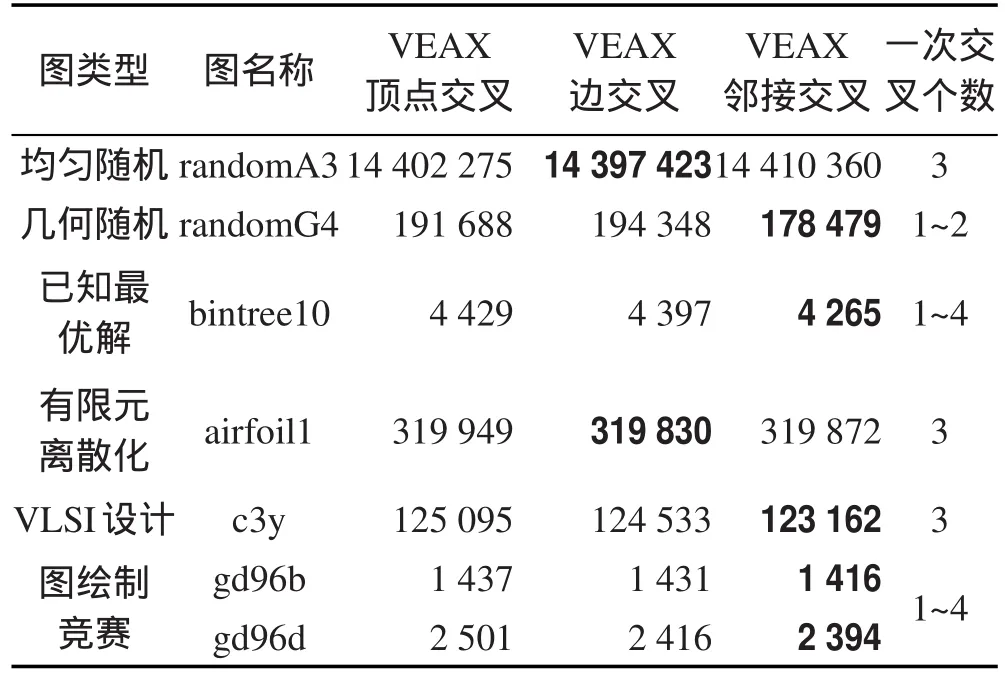
Table 2 Comparison of VEAX convergence with 3 kinds of crossover表2 3种交叉类型VEAX收敛性比较

Table 3 Comparisonof VEAX convergence with deferent accept_α表3 不同accept_α取值VEAX收敛性比较

实验结果表明,交叉类型“边交叉”和“邻接交叉”的启发性明显优于“顶点交叉”，依据不同类型图的特点确定交叉类型、cross_VEAnumber和accept_α，可更为充分体现VEAX良好的收敛性能，进而更为有效提高算法的近优解质量。

5 结束语

本文依据MinLA问题优化目标的特性及其可行域总是连通的特点，将“边”或“顶点及其任意个邻接点”作为交叉基因片段，在交叉算子内部流程结合爬山法的优势，采用迂回爬山策略，设计可灵活变型的顶点-边-邻接交叉算子VEAX，可更为高效地交叉生成高质量的后代个体，是提高算法整体性能的主要因素。其次为算法框架方面，利用Memetic算法兼具全局探测性和局部搜索性的优点，采用爬山法选择后代，并协调全局与局部搜索，使得算法在近优解质量与运行时间之间达到良好的平衡。设定不同参数阈值以生成不同特征的初始解，以及动态更新种群等保持种群多样性与同质性平衡的策略，也是保证算法具有较高进化效率的必要基础。实验表明，与最近的整体性能最好的两个算法TSSA和SSPR相比，基于以上策略的Memetic爬山算法整体性能明显更好。针对问题特点而设计的VEAX具有良好的收敛性能，其设计思想可为研究其他类似问题启发式算法所借鉴。后续研究的重点将是更为深入分析MinLA问题的特点，提出更为精细的初始解生成和种群多样性调节等策略，并结合其他搜索方法的优势和自适应机制，进一步提高算法整体性能和鲁棒性。此外，结合多层技术以扩大算法可有效处理问题规模，也将作为后续主要研究方向之一。

[1]Diaz J,Petit J,Serna M.A survey of graph layout problems [J].ACM Computing Surveys,2002,34(3):313-356.

[2]Petit J.Addenda to the survey of layout problems[J].Bulletin of EATCS,2013(105):177-201.

[3]Liu Xu.Researeh on load balancing algorithms based on graph partitioning and graph layout[D].Mianyang,China: ChinaAcademy of Engineering Physics,2008.

[4]Poranen T.A genetic hillclimbing algorithm for the optimal linear arrangement problem[J].Fundamenta Informaticae, 2005,68(4):333-356.

[5]Rodriguez-Tello E,Hao J K,Torres-Jimenez J.Memetic algorithms for the MinLA problem[C]//LNCS 3871:Proceedings of the 7th International Conference on Artificial Evolution, Lille,France,Oct 26-28,2005.Berlin,Heidelberg:Springer, 2006:73-84.

[6]Rodriguez-Tello E,Hao J K,Torres-Jimenez J.An effective two-stage simulated annealing algorithm for the minimum linear arrangement problem[J].Computers&Operations Research,2008,35(10):3331-3346.

[7]Martí R,Pantrigo J J,Duarte A,et al.Scatter search and path relinking:a tutorial on the linear arrangement problem [J].International Journal of Swarm Intelligence Research,2011, 2(2):1-21.

[8]Petit J.Experiments on the minimum linear arrangement problem[J].Journal of Experimental Algorithmics,2003,8:112-128.

[9]Areibi S.Effective exploration&exploitation of the solution space via memetic algorithms for the circuit partition problem[M]//RecentAdvances in MemeticAlgorithms.Berlin,Heidelberg:Springer,2005:161-182.

[10]Tang Maolin,Yao Xin.A memetic algorithm for VLSI floorplanning[J].IEEE Transactions on Systems,Man,and Cybernetics:Part B Cybernetics,2007,37(1):62-69.

[11]Chen Jianli,Zhu Wenxing,Ali M M.A hybrid simulated an-nealing algorithm for nonslicing VLSI floorplanning[J]. IEEE Transactions on Systems,Man,and Cybernetics:Part CApplications and Reviews,2011,41(4):544-553.

[12]Chen Jianli,Zhu Wenxing,Peng Zheng.A heuristic algorithm for the strip packing problem[J].Journal of Heuristics,2012,18(4):677-697.

[13]Nagata Y,Kobayashi S.A powerful genetic algorithm using edge assembly crossover for the traveling salesman problem [J].INFORMS Journal on Computing,2013,25(2):346-363.

[14]Lin Geng,Zhu Wenxing.An efficient memetic algorithm for the max-bisection problem[J].IEEE Transactions on Computers,2014,63(6):1365-1376.

[15]Freitas A R R,Silva V M R,Campelo F,et al.Optimizing two-level reverse distribution networks with hybrid memetic algorithms[J].Optimization Letters,2014,8(2):753-762.

[16]Chen Xiongfeng,Wu Jinglan,Zhu Wenxing.An enhanced hybrid genetic simulated annealing algorithm for VLSI standard cell placement[J].Pattern Recognition and Artificial Intelligence,2014,27(9):815-825.

[17]Chen Xiongfeng,Wu Jinglan,Zhu Wenxing.An effective genetic algorithm for VLSI standard cell array placement[J]. Journal of Xiamen University:Natural Science,2014,53(6): 797-803.

[18]Fiduccia C M,Mattheyses R M.A linear-time heuristic for improving network partitions[C]//Proceedings of the 19th Conference on Design Automation,Las Vegas,USA,Jun 14-16,1982.Piscataway,USA:IEEE,1982:175-181.

[19]Bar-Yehuda R,Even G,Feldman J,et al.Computing an optimal orientation of a balanced decomposition tree for linear arrangement problems[J].Journal of Graph Algorithms andApplications,2001,5(4):1-27.

[20]Petit J.Combining spectral sequencing and parallel simulated annealing for the MinLA problem[J].Parallel Processing Letters,2003,13(1):77-91.

[21]Safro I,Ron D,Brandt A.Graph minimum linear arrangement by multilevel weighted edge contractions[J].Journal ofAlgorithms,2006,60(1):24-41.

附中文参考文献：

[3]刘旭.基于图剖分和图排序的负载平衡算法研究[D].绵阳:中国工程物理研究院,2008.

[16]陈雄峰,吴景岚,朱文兴.VLSI标准单元布局问题的增强型混合遗传模拟退火算法[J].模式识别与人工智能, 2014,27(9):815-825.

[17]陈雄峰,吴景岚,朱文兴.VLSI标准单元阵列布局问题的一个高效遗传算法[J].厦门大学学报:自然科学版,2014, 53(6):797-803.

CHEN Xiongfeng was born in 1969.He received the M.S.degree from Fuzhou University in 2006.Now he is an associate professor at Minjiang University.His research interests include intelligent computing and software engineering,etc.

陈雄峰（1969—），男，福建仙游人，2006年于福州大学获得硕士学位，现为闽江学院副教授，主要研究领域为智能计算，软件工程等。

CHEN Zhen was born in 1984.He is a Ph.D.candidate at Fuzhou University.His research interest is optimization theory and algorithm.

陈振（1984—），男，福建莆田人，福州大学博士研究生，主要研究领域为最优化理论与算法。

XU Ge was born in 1978.He received the Ph.D.degree from Peking University in 2012.Now he is an associate professor at Minjiang University.His research interests include natural language processing and sentiment analysis,etc.徐戈（1978—），男，浙江淳安人，2012年于北京大学获得博士学位，现为闽江学院副教授，主要研究领域为自然语言处理，情感分析等。

Memetic Hill ClimbingAlgorithm for Minimum LinearArrangement Problemƽ

CHEN Xiongfeng1,2+,CHEN Zhen3,XU Ge1,2
1.Department of Computer Science,Minjiang University,Fuzhou 350121,China
2.Fujian Provincial Key Laboratory of Information Processing and Intelligent Control,Fuzhou 350121,China
3.Center for Discrete Mathematics and Theoretical Computer Science,Fuzhou University,Fuzhou 350108,China
+Corresponding author:E-mail:chenxf2000126@126.com

According to the properties of optimization objective of the minimum linear arrangement(MinLA)problem,and considering that the feasible region of the problem is always connected,this paper presents a new Memetic hill climbing algorithm for solving the MinLA problem.It combines the framework of Memetic algorithm and the internal procedure of its main operators with hill climbing method simultaneously,and adopts an indirect-climbing strategy in the internal procedure of its main operators.It uses a specific variable-type crossover operator named vertexedge-adjacent crossover,improves the algorithm for generating initial solutions based on greedy randomized adaptive search procedure(GRASP),and adopts the strategies including dynamic updating for maintaining population diversity. Compared with two recent algorithms named two-stage simulated annealing(TSSA)and scatter search and path relinking (SSPR),the experimental results on the acknowledged test suite show that the proposed algorithm has better compre-hensive performance.In the same average running time,the proposed algorithm improves the quality of the near-optimal solutions by an average of 1.6%and 2.01%respectively,and obtains the best near-optimal solutions at that time for 13 instances from the 21 test instances,which is more 4 than TSSAand more 2 than SSPR.

minimum linear arrangement;Memetic algorithm;hill climbing method;adjacent crossover

10.3778/j.issn.1673-9418.1601065

A

TP18

*The National Natural Science Foundation of China under Grant No.61170308(国家自然科学基金);the National Natural Science Foundation for Young Scholars of China under Grant No.61300156(国家自然科学基金青年科学基金).

Received 2016-01,Accepted 2016-04.

CNKI网络优先出版:2016-04-01,http://www.cnki.net/kcms/detail/11.5602.TP.20160401.1614.004.html