编码加扰序列的帧同步盲识别
马 钰,张立民,王好同
(海军航空工程学院电子信息工程系,山东烟台 264001)
编码加扰序列的帧同步盲识别
马 钰,张立民,王好同
(海军航空工程学院电子信息工程系,山东烟台 264001)
在同步情况下,基于对偶码可有效重建线性扰码的反馈关系,但非合作通信方同样需要完成盲同步.在无噪声条件下,针对编码加扰序列的盲同步问题,结合反馈多项式检测提出了帧同步盲识别算法.利用初始帧同步中探测的反馈多项式倍式集,可同时完成扰码反馈多项式和扰码序列的估计.实现初始同步后,可借助解扰数据帧结构属性完成精确同步;然后,将算法推广到了含噪信道情况;最后,基于Walsh-Hadamard变换给出了检测统计量的规范计算方案,以降低计算复杂度.
对偶码;帧同步扰码;线性反馈移位寄存器;盲同步;Walsh-Hadamard变换
1 引言
在数字通信中,通过序列加扰的方式可以将信息序列变换成近似随机的序列.在通信参数缺失的情况下,非合作第三方需要排除干扰并恢复扰码序列,才能获得信息序列.通信中数据往往按帧传输,因此在恢复扰码之前,需要首先完成帧同步.
线性扰码分为同步扰码和自同步扰码两种类型,可通过线性反馈移位寄存器(LFSR)产生.因为自同步扰码具有误码扩散特性,所以在无线通信中通常使用同步扰码.由于信道编码后信源的有偏性几乎消失[1],再加上扰码序列本身具有伪随机特性,所以在扰码未知的情况下基于相关分析的盲同步方案[2]将不再直接适用.因此,考虑结合扰码重建算法进行帧同步盲识别.
非合作直接序列扩频信号中的伪随机(PN)序列估计算法[3~5],由于其中PN序列的线性复杂度相对较低,以及和信息的作用方式,与扰码序列存在显著差别,所以不适用于扰码重建.扰码重建主要包括两个方面:反馈多项式的检测和初始状态的恢复[6].文献[7]利用组合枚举和快速相关攻击构建了伪随机扰码的快速盲恢复,其中利用组合枚举求解反馈函数的方法,在抽头系数较少的情况下才较为适用;文献[8]提出了基于Walsh-Hadamard变换的含错扰码序列生成多项式测定算法,其需要较为准确的估计反馈函数的阶数信息;文献[9]给出了含错m序列本原多项式的高阶统计测定算法,核心算法本质上与文献[6]中检测信源有偏性一致,不同在于模型中将误码视为一种有偏性较大的信源.但上述算法模型中均未考虑原始信息序列,仅是对扰码序列本身或受到信道误码后的攻击.基于信源有偏性Cluzeau提出了搜索低重量倍式的反馈多项式检测算法[6];为提高检测性能,文献[10]进一步修正了假设中的方差参数,提出了避免错误检测的方案;假设源bit流经前向纠错编码之后被加扰,文献[1]使用对偶码进行了扰码序列重建;文献[11]进一步提高了文献[1]中重建算法在含噪信道中的性能.通信中数据往往按照一定分组或帧进行传输,本文将结合基于对偶码的扰码重建技术,研究帧同步的盲识别问题.
2 系统模型
同步扰码器将输入信息序列与伪随机序列组合生成加扰序列,因为LFSR具有良好的统计特性和便于硬件实现,所以通常使用LFSR产生伪随机的扰码序列.一个LFSR序列可通过反馈多项式和初始状态唯一确定.将信息序列经编码后与扰码序列{st}进行模-2加,生成加扰序列{yt}(图1,图2),即yt=ct⊕st,t≥0其中⊕表示模-2加运算.

考虑线性分组码作为信道编码的情况,对于(n,k)线性分组码C,其中k是信息bit数量,n是编码bit数量,生成矩阵可表示为k×n维矩阵G.编码器可将k个bit的信息x=[x0,x1,…,xk-1]变换成n个bit的码字c=[c0,c1,…,cn-1].假设C的校验矩阵为(n-k)×n维矩阵H,H的行向量h0,h1,…,hn-k-1可扩展为对偶空间C┴.C中任意码字正交于所有H的行向量,即对任意c∈C,cHT=0.h0,h1,…,hn-k-1称为对偶码.
令L表示LFSR的长度,P(x)表示LFSR的反馈多项式.如果P(x)=1+c1x+…+cLxL,那么,由LFSR生成序列满足st+L=c1st+L-1⊕c2st+L-2⊕…⊕cLst,t≥0.其中c1,…,cL∈{0,1}.
编码后序列以Nb个bit组成一帧(图3),其中Nb可被n整除(令Nf=Nb/n),每帧信息使用相同的扰码进行加扰.帧同步过程建模为,确定接收bit位置到帧起始bit位置的偏移量Δt(图4),-Nb+1≤Δt≤Nb-1.

3 无噪声情况下帧同步算法
利用信号相关性是盲同步算法常采用的方案,例如基于自相关矩阵的Frobenius范数[2],或者基于数据的似然性[13]等.下面以相关函数为例分析加扰数据的相关性,由扰码序列的伪随机特性得,
E{yi⊕yj+Nb}=E{si⊕c⊕sj⊕c′}

(1)
其中c和c′表示数据bit.当数据bit未知时,认为服从等概率分布,则E{c⊕c′}也等于1/2.由式(1)可知,加扰后扰码的伪随机性与数据bit的随机性相互作用,因此,在数据未知或者扰码未知的情况下,不能利用数据间的相关性进行同步位置的盲识别,而需要联合扰码重建算法进行.
基于对偶码的扰码重建[1],首先需要将接收序列{yt}按长度n进行分组得到y0,y1,…,即yt=[ynt,…,y(n+1)t-1].通过与对偶码进行点积运算,可生成一个新的序列{rt}.不失一般性,假设一对偶码为h0=[h0,0,…,h0,n-1],那么
(2)
算法1 无噪情况下帧同步算法
(1)遍历所有可能偏移量Δt=-Nb+1,…,0,…,Nb-1;
(2)取出长度为Nb的接收bit序列{yΔt,yΔt+1,…,yΔt+Nb-1},按长度n进行分组得到y0,Δt,y1,Δt,…,yNf-1,Δt,其中yt,Δt=[yΔt+nt,yΔt+nt+1,…,yΔt+n(t+1)-1];

(4)遍历所有候选倍式集{Q(x)},0 (5)初始化Z=0; (6)t从id-1增加到Nb,计算 (3) Z=Z+(-1)zt; (7)令Nc=Nf-id-1+1,如果Z≥Nc/2,则计算其余偏移量下的统计量Z.如果某一时刻使得统计量等于Nc,那么其对应的偏移位置即为帧同步位置; (8)重复步骤1至步骤7,直到找到帧同步位置或者完成所有遍历. 上述算法中,在同步时刻检测倍式的统计量应等于Nc,而在非同步时刻倍式检测统计量应小于Nc,利用这一属性可实现帧同步位置的初步判别.根据文献[1],当Nc=50时,倍式判决的虚警概率Pf<10-10.仿真验证中,初始位置偏差为-351,搜索范围D=50,d=3,4,5,不同情况下的仿真结果见表1.仿真结果中,出现连续相邻的多个同步估计位置,一方面是由于前后相邻的几个bit恰好满足校验关系,或者对偶空间中存在满足循环移位关系的对偶码;另一方面,编码类型对于同步算法的影响主要体现在分组长度不同上,会使得新生成序列具有不同的反馈关系[11];另外,帧长度的影响主要是体现在截取扰码序列的长度上,与初始状态的影响相似,具有随机性.因此,此时称为粗同步,仍需要进一步处理才能确定正确的帧起始位置. 表1 无噪情况下帧同步仿真结果 在获得粗同步后,就可根据扰码重建算法恢复反馈多项式[1],并基于快速相关攻击算法[12]以及新序列与原始序列之间的关系,恢复LFSR的初始状态.解扰后的数据应具有相似的帧结构特征,否则,应当在粗同步位置及其附近继续进行搜索.当解扰后的数据出现有意义的帧结构信息时,可获得精确同步. μ1=(Nf-id-1+1)(2ε)wd (4) (5) 在进行倍式判别时,可基于以下两个假设: H1:Z~N(μ1,σ12),Q(x)是P(x)的倍式. 其中Nc=Nf-id-1+1.将式(4)和式(5)带入上式可得: 与无噪情况下类似,得到帧同步算法如算法2. 算法2 含噪情况下帧同步算法 (1)遍历所有可能偏移量Δt=-Nb+1,…,0,…,Nb-1; (4)遍历所有候选倍式集{Q(x)},0 (5)初始化Z=0; (6)t从id-1增加到Nb,计算 (6) Z=Z+(-1)zt; (7)计算判决门限T,均值μ1,标准差σ1.如果Z≥T/2,则计算其余偏移量下的统计量Z(Q(x),Δt).如果Z(Q(x),Δt)>T,则Q(x)为倍式,执行下一步;否则,重复步骤(1)至步骤(7),直到找到倍式或者所有遍历完成. (8)在倍式对应的最大统计量处的偏移量下,进行其他倍式的检测,得到倍式集合{Q(x)}.假设集合中包含NQ个倍式. (9)计算各偏移量下倍式判决的平均可信度(图5),平均可信度最大的偏移位置作为粗同步位置返回.判决可信度及平均可信度分别定义为: (7) (8) 同步过程中采用了平均可信度最大准则,即在同步位置处倍式判决的可信度应达到峰值.由式(7)可知,判决可信度位于区间(0,1)内.在加性Gauss白噪声信道中,可采用不同帧的匹配滤波数据降低新构造序列的误码率[11].因此,仿真验证中假设误码率为10-3,其他仿真条件与无噪声情况相同,不同情况下的仿真结果见表2.为加快算法收敛速度,步骤(8)使用了步骤(7)中倍式对应最大统计量处的偏移量,同时此做法可能会造成算法陷入局部最优解,无法完全检测到测试集中所有倍式,更加稳健的方法中应重复步骤(1)至步骤(7)搜索倍式集合.在完成初始同步后,同样需要结合帧结构信息对解扰数据进行精确同步. 表2 含噪情况下帧同步仿真结果 基于倍式搜索的扰码反馈多项式重建算法,其计算复杂度主要体现在搜索空间大小,以及检测统计量的计算上.遍历所有可能偏移量Δt的过程,使得盲同步算法复杂度成倍增加,因此,提出基于Walsh-Hadamard变换的计算方法,以提高算法运算效率. 文献[14]在讨论“利用Walsh函数解二元域方程组”的应用时指出,Walsh-Hadamard变换后谱系数的物理意义可表示为使方程组成立的个数与不成立个数之差.因此,可基于Walsh-Hadamard变换进行检测统计量Z的计算. 使用Walsh-Hadamard变换方法,仅需要进行一次原数据的统计,即构造向量a的过程.这样可以节省在算法遍历过程中式(3)和式(6)计算zt的时间,代价是需要计算Hadamard矩阵中特定元素的值.但Hadamard矩阵中元素的取值是固定的,可通过查表方式获得,因此可以忽略计算Hadamard矩阵中元素值的复杂度.鉴于解算问题的规模(表征为D,如:50),构造向量a时将出现大量的0元素,所以建立位置-频次(u-fu)字典以节省存储空间和提高运算速度.不同的倍式对应Hadamard矩阵中不同的列,遍历字典即可计算检测统计量Z.结合Walsh-Hadamard变换的物理意义和统计量Z的表达式,可得到基于Walsh-Hadamard变换计算Z的方法如下: (1)将生成序列{rt}按长度D进行有重叠连续分组,并进行十进制转换,即将rtrt+1…rt+D-1转换成十进制数,Nf个数据将生成Nf-D+1个十进制数. (2)用这Nf-D+1个十进制数构造位置-频次(u-fu)字典(对应矢量a中的位置u和元素值fu,即将矢量a中第u个元素的所在位置标记为u-1,第u个元素的取值等于u-1在Nf-D+1个十进制数中出现的次数,1≤u≤2D). (3)多项式Q(x)=1+xi1+…+xid-1对应2D阶Hadamard矩阵的第v列,其中v-1等于Q(x)的二级制表示(图6)对应的十进制数值,1≤v≤2D. 图6Q(x)=1+xi1+…+xid-1的二进制表示 (4)遍历字典进行累和,计算检测统计量 (9) 基于Walsh-Hadamard变换计算检测统计量时,对于不用阶数的倍式进行统计的zt数量是一定的(Nf-D+1),避免了由于多项式变化需要重新计算不同假设下的均值和方差,从而可以使用固定的判决门限,和直接使用检测量的统计值表示判决可信度.这样的代价是,统计数量减少,而降低判决的可靠性. 本文结合基于对偶码的扰码重建算法研究了帧同步盲识别问题.首先,在无噪声情况下,利用扰码重建算法中检测统计量等于特定值的属性,可初步识别帧同步位置.在完成粗同步后,即可重建扰码序列以解扰数据,再结合帧结构的特征实现精确同步位置的识别;其次,以平均判别可信度最大为帧同步识别准则,将无噪情况下的帧同步识别算法推广到含噪情况;最后,研究了基于Walsh-Hadamard变换的检测统计量计算方法,以构建标准化的计算模式,便于编程实现和降低算法复杂度.Walsh-Hadamard变换方法,不适用于高误码率情况,可采用文献[11]中的多信息流算法降低数据误码率. 文中假设了对偶码参数已知,更具挑战性的问题是同时重建对偶码和扰码[1],利用重建算法中的判决过程,再结合上述同步框架,完成帧同步盲识别.在使用自同步扰码的情况下,可结合自同步扰码重建算法[16],推广本文算法进行同步识别. [1]X B Liu,S N Koh,C C Chui,et al.A study on reconstruction of linear scrambler using dual words of channel encoder[J].IEEE Trans Inf Forens Security,2013,8(3):542-552. [2]牟青,魏平.基于缺失数据模型的长码直扩信号的伪码估计[J].电子学报,2010,38(10):2365-2369. Mou Qing,Wei Ping.Spreading waveform estimation of long-code DS-SS signals based on missing-data model[J].Acta Electronica Sinica,2010,38(10):2365-2369.(in Chinese) [3]谢春辉,程义民,陈扬坤.PN序列估计与扩频隐藏信息分析[J].电子学报,2011,39(2):255-259. Xie Chun-hui,Cheng Yi-min,Chen Yang-kun.PN sequence estimation and spread-spectrum steganalysis[J].Acta Electronica Sinica,2011,39(2):255-259.(in Chinese) [4]任啸天,徐晖,黄知涛,等.基于Fast-ICA同、异步系统短码CDMA信号扩频序列与信息序列盲估计[J].电子学报,2011,39(12):2726-2732. Ren Xiao-tian,Xu Hui,Huang Zhi-tao,et al.Fast-ICA based blind estimation of spreading and information sequences of short-code CDMA signals in synchronous and asynchronous systems[J].Acta Electronica Sinica,2011,39(12):2726-2732.(in Chinese) [5]任啸天,徐晖,黄知涛,等.基于Fast-ICA的CDMA信号扩频序列优化盲估计[J].电子学报,2012,40(8):1532-1538. Ren Xiao-tian,Xu Hui,Huang Zhi-tao,et al.Fast-ICA based optimize blind estimation of spreading sequence of CDMA signals[J].Acta Electronica Sinica,2012,40(8):1532-1538.(in Chinese) [6]M.Cluzeau.Reconstruction of a linear scrambler[J].IEEE Trans Comput,2007,56(9):1283-1291. [7]罗向阳,沈利,陆佩忠,等.高容错伪随机扰码的快速盲恢复[J].信号处理,2004,20(6):552-558. Luo Xiang-yang,Shen Li,Lu Pei-zhong,et al.Fast blind restore of LFSR sequences with high error tolerance[J].Signal Processing,2004,20(6):552-558.(in Chinese) [8]伍文君,黄芝平,唐贵林,等.含错扰码序列的快速恢复[J].兵工学报,2009,30(8):1134-1138. Wu W J,Huang Z P,Tang G L,et al.Fast recovery of interfered scrambling code sequence[J].Acta Armamentarii,2009,30(8):1134-1138.(in Chinese) [9]苏绍璟,伍文君,黄芝平,等.含错m序列本原多项式的高阶统计测定算法[J].兵工学报,2010,31(12):1593-1598. Su Shao-jing,Wu Wen-jun,Huang Zhi-ping,et al.Blind identification of the primitive polynomial of m-sequence with error using high-order statistic[J].Acta Armamentarii,2010,31(12):1593-1598.(in Chinese) [10]X B Liu,S N Koh,X W Wu,et al.Reconstruction of a linear scrambler with improved detection capability and in the presence of noise[J].IEEE Trans Inf Forens Security,2012,7(1):208-218. [11]Yu Ma,Li-min Zhang,Hao-tong Wang.Reconstructing synchronous scrambler with robust detection capability in the presence of noise[J].IEEE Trans Inf Forens Security,2015,10(2):397-408. [12]T Johansson and F Jønsson.Improved fast correlation attacks on stream ciphers via convolutional codes[A].Advances in cryptology[C].Prague,Czech Republic:Springer-Verlag,1999.347-362. [13]Shaodan Ma,Xinyue Pan,Guang-Hua Yang,et al.Blind symbol synchronization based on cyclic prefix for OFDM systems[J].IEEE Trans Veh Technol,2009,58(4):1746-1751. [14]游凌,朱中梁.Walsh函数在解二元域方程组上的应用[J].信号处理,2000,16 (增刊):27-30. You Ling,Zhu Zhong-liang.The application of Walsh Function in Resolving of F(2) equations[J].Signal Processing,2000,16(supplement):27-30.(in Chinese) [15]N.Ahmed,K.R.Rao.Orthogonal Transforms for Digital Signal Processing[M].胡正名,陆传,译.北京:人民邮电出版社,1979. [16]廖红舒,袁叶,甘露.自同步扰码的盲识别方法[J].通信学报,2013,34(1):136-143. Liao Hong-shu,Yuan Ye,Gan Lu.Novel blind reconstruction method for self-synchronized scrambler[J].Journal on Communications,2013,34(1):136-143.(in Chinese) 马 钰 男,1986年生于山西寿阳.海军航空工程学院电子信息工程系博士生,助理工程师.研究方向为综合电子战系统、非合作数字信号处理. E-mail:my7202359@126.com 张立民(通信作者) 男,1966年生.海军航空工程学院教授,博士生导师.研究方向为综合电子战系统与技术、军用仿真技术. E-mail:iamzlm@163.com 王好同 男,1958年生.海军航空工程学院副教授,硕士生导师.研究方为航空通信与导航. E-mail:haotong-1958@126.com Blind Identification of Frame Synchronization in Scrambled Coding SequenceMA Yu,ZHANG Li-min,WANG Hao-tong (DepartmentofElectronicandInformationEngineering,NavalAeronauticalandAstronauticalUniversity,Yantai,Shandong264001,China) With a dual word,we can reconstruct the feedback polynomial of a linear scrambler when the synchronization is complete.An eavesdropper must achieve synchronization before recovering scrambler.Based on the algorithm of reconstruction of linear scrambler,we present techniques to achieve blind synchronization.We can get a set of multiples of the feedback polynomial when course synchronization is complete.Meantime,we can also recover the feedback polynomial and a scrambler sequence.Then,we need architecture of frame to achieve fine synchronization with the descrambled data.The study is based on the assumption that the channel is noiseless and then extended to the noisy channel condition.In order to reduce the computational complexity,we also propose a normal scheme to compute the statistic on the base of Walsh-Hadamard transformation. dual word;frame synchronous scrambler;linear feedback shift register (LFSR);blind synchronization;Walsh-Hadamard transformation 2015-01-21; 2016-01-06;责任编辑:蓝红杰 泰山学者工程专项经费 TN919 A 0372-2112 (2016)09-2087-06 ��学报URL:http://www.ejournal.org.cn 10.3969/j.issn.0372-2112.2016.09.010
4 含噪情况下帧同步算法





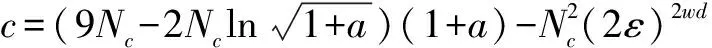






5 基于Walsh-Hadamard变换的计算方法

6 结束语



