基于SIFT图像拼接算法在钢轨三维形貌测量的应用
◎何威威 王泽勇 李金龙 罗林
基于SIFT图像拼接算法在钢轨三维形貌测量的应用
◎何威威 王泽勇 李金龙 罗林
钢轨三维形貌测量对行车安全有重要的意义,而铁路运营的里程越来越长,为了更准确、高效地复原和测量钢轨的三维形貌,需要对测量图像进行拼接。本文对Harris、SUSAN和SIFT三种图像拼接算法进行了仿真分析和比较,对这三种方法的拼接效果做了评价,仿真结果表明SIFT算法的拼接效果最佳。本文将SIFT算法与FTP相结合,应用于钢轨的三维形貌测量,将拼接后的图像进行FTP复原,得到很好的钢轨三维复原相貌。
随着铁路向重载化和高速化发展,钢轨的磨耗愈加严重,这将会使得火车在运行中发生摇摆和振动,影响旅客舒适度,严重时可能出现脱轨及侧翻事故,带来严重的安全隐患,因此需要及时对钢轨的磨耗量进行测量。
对钢轨磨耗的测量,有接触式和非接触式两种,接触式测量在20世纪70年代有应用,缺点是需要与钢轨进行接触,设备本身也会有损耗,不能完整地复原钢轨原貌,而近年来出现了非接触式的钢轨三维形貌测量的技术,其中FTP(傅里叶变换轮廓 术:Fourier Transform Profilmetry)是钢轨三维形貌测量最有效的方法之一。FTP只需一帧变形条纹图像即可实现物体的三维形貌测量,因此具有复原速度快,精度高等优点。然而鉴于每一帧图像的视场范围有限,对于长距离的钢轨复原,需要采用图像拼接技术来实现。SIFT(尺度不变特征变换:Scale Invariant Feature Transform)是一种较好的方法,在缩放、旋转的情况下,能很好地完成拼接。
基本原理
FTP原理
FTP光路原理图如图1所示,P1和P2分别为投影系统的入瞳与出瞳,I1和I2分别为照相系统的出瞳与入瞳,d为P2与I2间的距离,L0是从I2到参考平面之间的距离,A和C是参考面上的两点,D是物体表面的点,光栅垂直于图平面。
用正弦光栅投影到被测物体表面,得到变形结构光场的表达式为:
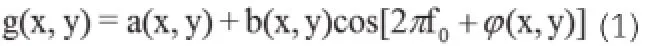
其中,a(x,y)为背景光场,b(x,y)是条纹对比度,φ(x,y)是经过物体之后产生的相位,f0投影光栅的基频。对条纹进行傅里叶变换得到其频谱分布,在x方向上一维傅里叶频谱表示为:
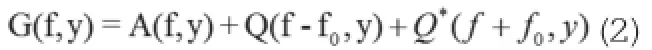
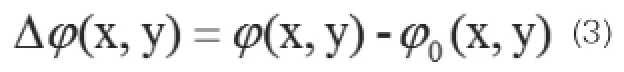
根据投影关系,就可以得到:
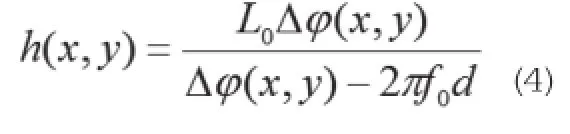
SIFT算法拼接原理
二维高斯函数
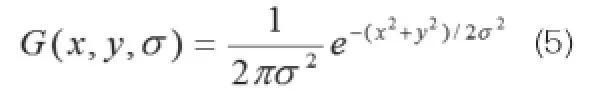

图像I(x, y)在不一样的尺度下和高斯函数进行卷积,得
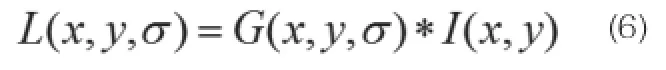
其中σ是空间尺度因子,因子越小,则图像被平滑得越少,反之则越多,L(x,y,σ)表示图像的尺度空间。
经过SIFT算法进行特征匹配,找到不受图像缩放、旋转影响的特征点,用RANSAC算法进行特征点提纯,使得图像的特征点匹配更加精确,加权算法的数据融合,让两幅图像融合成为一幅图像。
仿真与分析
对如图2所示的两幅有重叠的图像,分别采用SIFT,SUSAN及Harris三种拼接方法进行拼接,并用RANSAC进行特征点提纯及加权算法进行图像融合,结果如图3所示。
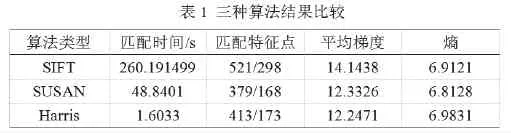
对上述的图像进行评价比较,如表1所示:
从表1可见, Harris和SUSAN拼接算法使用的时间较少,但SIFT能够匹配的数目较多,准确率也比较高,显然找到拼接位置的点的概率也会较高;从平均梯度来看,数值大说明SIFT算法拼接的图像对于微小细节反差的表达能力较好;从熵的角度看,SIFT拼接算法在三种处于中等。而从图3实际的拼接效果看,Harris拼接算法较差,而从表1分析,SUSAN拼接算法微小细节反差的表达能力又没SIFT拼接算法好。综上所述,选择SIFT算法性能较佳。
在钢轨三维形貌测量中的应用
对上述的图像进行客观的评价,如表2:



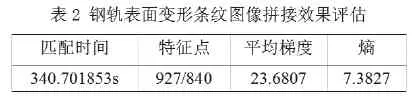


从表2可以看出,对钢轨三维形貌测量图像用SIFT算法进行粗匹配和RANSAC算法进行精确匹配后,两幅图(图5)匹配经历的时间为340.701853s,粗匹配的特征点有927个(图6),精确匹配的特征点有840个(图7)。拼接及图像融合后的图像如图7,平均梯度的数值比较大,说明SIFT拼接算法对微小细节反差的表达能力好,而熵的数值比较小,说明图像质量离散程度不高,因此SIFT拼接算法比较适合用在钢轨三维形貌测量。
采用FTP方法,对拼接图像进行三维重建,其复原图如图8所示:
从复原来看,边缘还有些瑕疵,表面看起来复原得比较好。从复原来看,尽管边缘有些误差,但整体复原得较好。系统经过标定后即可获取钢轨三维形貌尺寸,与标准钢轨对比后即可获取磨耗量。理论和实践证明FTP方法的测量精度可达0.1mm以上。
通过仿真比较和分析,使用SIFT算法对变形条纹进行拼接,质量较好,同时将该方法应用于钢轨三维形貌测量,将两幅钢轨三维形貌变形条纹图像拼接和数据融合后,用FTP方法得到较好的钢轨三维形貌复原。实践证明,该方法用于钢轨表面磨耗测量是可行的,为钢轨三维形貌测量提供一种良好的方法借鉴。
(作者单位:西南交通大学物理科学与技术学院光电工程研究所)

