一种强背景噪声下的WSN目标定位算法

侯建军， 朱明强， 刘颖

(北京交通大学 电子信息工程学院， 北京 100044)



一种强背景噪声下的WSN目标定位算法

侯建军， 朱明强， 刘颖

(北京交通大学 电子信息工程学院， 北京 100044)

为了进一步提高无线传感器网络(WSN)目标定位解算精度，提出了一种改进的Cubature粒子滤波(ICPF)定位算法. 该算法运用最小二乘法估计移动目标当前初始时刻的位置，使用Cubature卡尔曼滤波和Gauss-Newton迭代法来充分利用测量更新后的状态最新信息，精确设计目标状态重要性密度函数，为粒子滤波提供相应的建议分布，从而能够更加有效改善粒子滤波器的性能. 仿真实验结果证明，提出的改进算法在强背景噪声下能有效提高定位精度且收敛性增强，其性能优于标准粒子滤波(PF)、扩展粒子滤波(EPF)及Unscented粒子滤波定位算法(UPF).

Cubature卡尔曼滤波；粒子滤波；无线传感器网络；目标定位

近年来随着物联网产业的兴起和蓬勃发展，无线传感器网络(wireless sensor network， WSN)这一新兴技术在诸如现代城市环境监测、交通运输导航追踪定位、商业物流配送管理、智能化社区服务乃至战场情报信息收集和公共安全等诸多领域得到了广泛应用，受到了高度关注. 其中，解决传感器节点自身位置感知问题成为无线传感器网研究领域工作的重点.

目标定位问题的任务是利用传感器获得一定的测量信息，对目标的当前状态进行精确的估计并对之后的状态进行预测，其通常体现为一个强非线性系统的状态最优或次优估计问题，国内外众多学者针对这一问题做了大范围多角度的探讨与研究. 美国学者Anindya S. Paul和Eric A. Wan[1]提出SPKS算法，使用Unscented卡尔曼滤波的思想进行定位解算，与扩展卡尔曼滤波(EKF)相比计算复杂度基本相同但定位精度更高. 一些国内学者[2-3]提出了基于改进的无迹卡尔曼滤波(IUKF)算法用于组合导航定位，利用球面分布单形采样降低了系统的计算复杂度，或利用自适应估计原理抑制模型误差. 但因其系统状态维数较高，采用标准UKF框架容易出现滤波发散问题，影响导航精度提升. 很多研究者[4-6]利用粒子滤波(particle filter， PF)算法处理定位问题取得较好效果，但是粒子随递推的延续会出现贫化现象，容易导致滤波失效. 近年来出现的多种利用线性化截断原理和确定采样型卡尔曼滤波框架改进粒子滤波算法[7-9]，为其提供准确建议分布的蒙特卡洛型定位方法，取得较好效果. 但是也存在如非线性误差增大，计算复杂度增高和实时性降低等问题.

本文针对WSN定位问题现状做了研究和分析，对定位模型参量进行了向量化解析，提出了一种改进的新型定位算法. 使用最小二乘法估计目标的初始位置，减小原始误差，后运用Gauss-Newton(G-N)迭代法结合Cubature卡尔曼滤波(CKF)获得更为准确的重要性密度函数，为粒子滤波法提供相应建议分布. 与标准PF，EPF 和 UPF 相比，改进算法ICPF因其能够充分利用最新的测量信息，且至少以三阶精度保证传递后状态统计量的分布，所以使得模型可信度更高，能够较好地提高目标定位精度.

1 目标定位问题模型研究

WSN精确目标定位通常采用测距式定位技术进行. 由于TOF测距技术具有测距范围广、测距精度较高和系统简单等特点，本文采用TOF技术测量目标节点和信标节点间距离. 其定位一般过程通常可分成目标侦搜、节点定位、状态预测和信息通知4个阶段.

1.1 系统纯方位定位模型

由于实际WSN环境中传感器节点接受到的无线信号观测量通常是一个非高斯时变量，受到环境噪声因素的影响明显，因此，目标定位是一个典型的强非线性问题. 为研究问题方便，设目标运动简化为二维平面，结果可推至三维. 目标节点(移动节点)坐标位置为(x,y)，信标节点(传感器节点)坐标位置为(xi,yi)，则目标节点运动状态方程和信标节点测量方程可分别表示为

(1)

(2)

式中目标状态向量为Xk=[xkyk]T；ur为已知的测量状态向量；Φk/k-1和Γ分别是状态转移阵和噪声转移阵；

wk-1和vk分别是状态噪声及测量噪声，其协方差分别为Qk-1和Rk. 本文限定考虑对状态的强非线性滤波问题，因此系统状态服从一阶马尔可夫过程，测量量独立于已知状态量.

1.2 WSN网络部署描述

信标节点按随机拓扑结构布置于网络当中，负责发射信号探测目标并采集和转发相应的数据，终端节点负责收集各信标节点传感器的数据，提取定位参数进行数据融合计算移动目标的位置.

定位测试系统网络中传感器采用休眠/唤醒机制，信标节点以固定发射功率不断发送数据包， 当接收到50个数据包后， 对平均值进行平滑处理. 然后将处理后的数据送给终端，终端将值转换成距离信息并进行定位计算， 该机制可以节省能量，延长传感器网络生存时间.

2 改进的Cubature粒子滤波算法

粒子滤波(particle filter，PF)是一种基于蒙特卡洛思想的非线性滤波方法，具有估计精度较高的特点. 但是其实现时容易出现粒子集贫化现象影响滤波效果，从而导致定位精度降低. 避免这种情况的有效方法是选取合适的建议分布函数. 本文使用Cubature卡尔曼滤波和Gauss-Newton迭代法来为粒子滤波设计合理的建议分布，提出一种基于迭代的粒子滤波运算改进方法，有效改善其滤波性能.

2.1 Gauss-Newton迭代法

Gauss-Newton(G-N)迭代法是解决最小二乘最优化问题常使用的一种方法，其本质是使用容积数值积分原则计算非线性函数的统计分布. 该方法基本思路是在进行每次迭代的过程中同时构造G-N方向，然后通过迭代运算框架，融合最新的测量信息，进行持续修正. 使得代价函数最小化，最终能够不断逼近最优解[10]. 基本过程如下：

① 根据系统对误差信息认知程度构造权重因子wi；

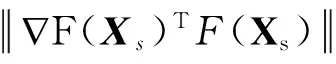
③ 根据初始点选取位置构造Gauss-Newton方向

④ Xi+1=Xs+Ds，s←s+1，跳至步骤②.

而无论目标(移动)节点的真实位置和初始迭代位置如何变化，G-N迭代法几乎都能收敛[10].

2.2 Cubature卡尔曼滤波特点及原理

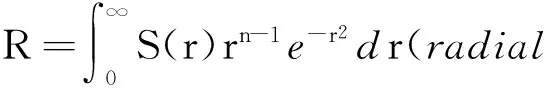
对于标准高斯分布根据上述法则可得

其中

由上述可知，CKF选取2n个同等权值的Cubature点计算高斯权重积分， 计算出Cubature点(ηi，ui)后可以通过卡尔曼滤波框架计算时间更新和测量更新得到CKF 滤波算法，其滤波精度与UKF基本相当，但是求取较为便捷且更适用于高维状态估计问题[11].

2.3 改进的粒子滤波定位算法

提高粒子滤波性能的关键是降低粒子贫化现象. 其中一个比较有效的方法是：在重要性密度函数中引入当前最新测量信息，使得采样粒子集中分布在高观测似然区域. 本文将Cubature卡尔曼滤波与粒子滤波相结合，利用确定型采样点集的Cubature变换设计更准确的重要性密度函数，并利用G-N迭代方法融合最新测量信息，改进定位算法如下：设网络中有数目≥3个的信标节点(传感器)，其坐标分别为(x1，y1)，(x2y2)…(xnyn)，目标节点(移动节点)的坐标为(x，y)，d为测量距离，则有

(3)

根据最小二乘法估计原理可解算得

(4)

将获得的初始位置信息X0代入改进的粒子算法框架当中，即可获得更加精确的移动目标状态信息. 结合G-N迭代法，改进Cubature粒子滤波定位算法的具体的步骤如下：

① 滤波初始化(k=0).

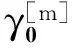
② 滤波运行(k=k+1).

a)粒子集预测更新：利用状态噪声协方差Q定位系统模型状态方程，依据Cubature粒子的预测更新法则进行处理，

(5)

(6)

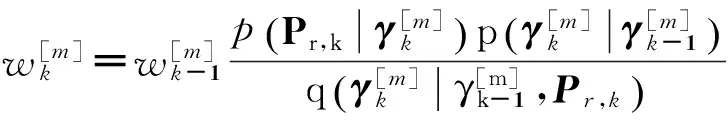
c)重采样：计算每一个粒子的归一化权值，粒子集权重归一化处理后进行随机重采样.

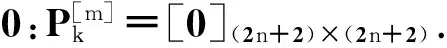
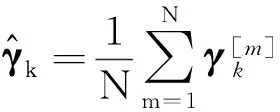
f)返回步骤②：将WSN定位系统方程进行离散化处理后代入式(5)～(6)算法框架进行处理，即可得系统移动目标状态向量参数最优估计值.

3 仿真实验

实验采用美国Jennic公司的JN5147集成通信模块和Matlab软件平台对算法性能进行数据测试和仿真分析. 选取1个100m×100m的实验场地随机的部署4个传感器节点(信标节点)，区域内所有目标均在其侦测范围内，并随时间可逐步增加节点数量. 在ZigBee通用无线平台上搭载JN5147通信模块，在传感器节点位置设置终端，在目标节点处设置匹配网关，并与计算机设备相连，用于采集与终端的TOF测距时间值.

(7)

式中：tps为测距时间；tot为往返测距时间；tRD为接收延时;txd为发送延时；tat为返程测距时间；RLRC为近距离补偿;RRRC为远距离补偿；Doffset为延时补偿. 将tps测距时间转换为距离值，测量距离则根据D=tpsc可计算出. c表示电磁波空间传播速度，可取3×10m/s，D表示TOF模式下的距离测量值.

目标移动过程中的状态噪声协方差阵为Q=diag[q q]，研究分析时可逐渐加大其数值. 设观测噪声协方差阵R=diag[6 4 4 6]，采样持续时间为50s，初始状态可由最小二乘法获得. 在Matlab环境假设粒子数分别N=10，30，50，100，迭代Cubature粒子滤波迭代次数i=2并可增加. 为与标准粒子滤波(PF)，扩展粒子滤波(EPF)及Unscented粒子滤波(UPF)比较定位算法精度，引入目标节点累加均方根误差，定义为

(8)

在噪声相对比较小(q=0.000 5)的条件下，此时绝大部分的粒子能够汇聚在真实值周围，因此标准PF算法在这种情况下极为稳定，用以实施定位解算性能较好. EPF和UPF算法用以设计生成重要性密度函数的关键分别是EKF和UKF方法. 由于EKF只是在固定点以Taylor级数展开，以一阶线性化截断近似进行状态变量的传递，不可避免引入误差且原始信息损失较大，它会使得原先集中在真实值附近的粒子变得分散，以此为粒子滤波提供建议分布反而使得滤波器性能下降. 而UKF方法则以确定性采样的方法获得Sigma点，通过非线性传递获得建议分布性能有所改善，但是仍然是不完全准确的，在状态噪声较小的时候，由于初始估计相差较小，此时ICPF与UPF和标准PF定位估计效果相比优势不明显.

如图3所示，当噪声加大到q=0.005时，标准PF出现明显的不稳趋势，其定位误差已经呈现出大幅波动状态，此时由于UKF和CKF因为均采用确定型采样点集，能够通过非线性变化尽可能真实逼近状态和测量两大非线性模型，均能以至少3阶精度保证非线性传递后状态量的分布，可以较好地解决似然函数过分尖锐和预测样本重叠区域过小的问题. 因此，其估计精度较高. 此时，UPF和ICPF定位精度平均要比EPF和PF高34%.

随着状态噪声进一步加大到q=0.05，估计误差随之增大，同时观测似然函数变得平缓，将使得被吸引到目标真实位置附近的预测粒子分布范围扩大，使得有效粒子数量会有所减少. 标准PF由于粒子贫化现象严重，随时间推移粒子预测不再准确，滤波呈现逐渐发散直至完全偏离，收敛性明显衰退，定位失效. EPF相对稳定，但图4可明显看出本文所提的ICPF算法与UPF相比，尤其是到了定位后半阶段，由于引入迭代滤波策略，在更新状态时可以充分利用最新的测量信息针对前次滤波基础对状态估计、协方差进行迭代修正，以近似0 残差使状态收敛到MAP估计，平滑状态一步预测误差，在先验误差不断累积情况下，比标准PF定位精度高出27%以上，平均定位精度最好，收敛速度快于EPF和UPF.

由表1可知中等状态噪声情况下采用不同粒子数目影响定位估计精度，当粒子数为10时，基于PF，EPF，UPF的定位算法与基于ICPF的蒙特卡罗定位算法的平均误差都超过2 m，当粒子数目增加到50且迭代次数为2时，ICPF平均误差降低为原先的38%，其定位估计误差总体上是标准PF的60%左右，当粒子数目接近50时，ICPF的定位估计精度基本趋于饱和，而PF和UPF粒子数接近100时才趋于饱和.N=50时，ICPF运算机制上仅比UPF增加了1～2次样点的迭代测量更新非线性变换，总体未改变运算复杂度的数量级，且与EPF相比无需计算雅克比行列式，在运算量和运算便捷性上ICPF具有一定优势. 使用Matlab定时器工具，可得3种滤波器的单次递推平均所需时间PF为0.897 s，EPF为1.741 s，UPF为1.517 s，ICPF为1.631 s. ICPF也仅仅比UPF多出4.2%，在提高估计精度的前提下同时保证了相对低的计算开销.

此外，通过仿真验证研究发现：迭代次数与状态估计精度并非是线性递增的关系. 当采用基于G-N法则的改进定位算法迭代次数达到3时，定位估计精度的提高效果已经趋于平缓，因此有限的2～3次迭代运算，即可获得较好的估计精度收益，完全可以满足WSN定位实时性要求.

表1 不同粒子数目时平均误差对比

Tab.1 Comparison of ARMSE based on the number of particles

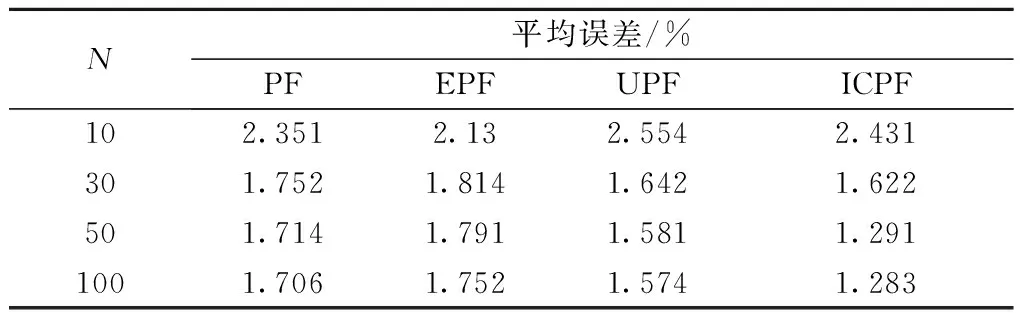
N平均误差/%PFEPFUPFICPF102.3512.132.5542.431301.7521.8141.6421.622501.7141.7911.5811.2911001.7061.7521.5741.283

4 结 论

针对WSN中移动目标节点定位问题，提出了一种基于改进的Cubature粒子滤波器(ICPF)的蒙特卡洛定位算法. 使用G-N迭代法充分利用最新测量信息，运用Cubature卡尔曼滤波获得准确的状态统计信息用以精确设计建议重要性函数，抑制了粒子贫化，改善了粒子滤波器性能，提高了状态估计精度. 仿真验证了其平均定位精度相较传统粒子滤波提高了27%，尤其是在背景噪声较大的情况下改善明显. 算法运行时间合理，能够满足定位实时性要求. 本文所提算法在改进WSN目标定位精度中具有一定参考价值，后续工作中将对距离获取方法和定位模型运行解算机制继续深入研究，以期进一步提高定位算法的适用性和应用性.

[1] Paul A S， Wan E A. RSSI-Based indoor localization and tracking using sigma-point Kalman smoothers[J]. IEEE J of Selected Topics in Signal Processing， 2009，3(5):860-873.

[2] 刘明雍，胡俊伟，李闻白.一种基于改进无迹卡尔曼滤波的自主水下航行器组合导航方法研究[J].兵工学报，2011，32(2):252-256．

Liu Mingyong， Hu Junwei， Li Wenbai. Research on integrated navigation for autonomous underwater vehicle based on an improved unscented kalman filte[J]. Acta Armamentarii， 2011，32(2):252-256. (in Chinese)

[3] 高为广，何海波，陈金平.自适应UKF算法及其在GPS/INS组合导航中的应用[J].北京理工大学学报，2008，28(6):505-509.

Gao Weiguang， He Haibo， Chen Jinping. An adaptive UKF algorithm and its application for GPS/INS integrated navigation system[J]. Transactions of Beijing Institute of Technology， 2008，28(6):505-509. (in Chinese)

[4] Khan Z， Balch T， Dellaert F. MCMC-based particle filtering for tracking a variable number of interacting targets[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2005，27(11):1805-1918．

[5] Guo Hui， Ji Hongbing， Wu Bim . Quasi-Monte Carlo Gaussian particle filter based target tracking for the multiple passive sensor[J]. Journal of Xidian University， 2010，37(6)：1042-1047.

[6] Ahmed N， Rutten M， Bessell T， et al. Detection and tracking using particle filter based wireless sensor networks[J]. IEEE Transaction on Mobile Computing， 2010(9):1-15.

[7] Li Liangqun， Ji Hongbing， Luo Junhui. The iterated extended Kalman particle filter[C]∥IEEE International Symposium on Communications and Information Technology. Xi’an: Xidian Univesity， 2005:1213-1216.

[8] 黄小平，王岩，李超，等.一种改进的粒子滤波在WSN目标跟踪中的应用[J].中南大学学报:自然科学版，2011，42(增刊1):895-899．

Huang Xiaoping， Wang Yan， Li Chao， et al. Application of an improved particle filter algorithm for target tracking in WSN[J]. Journal of Central South University: Science and Technology， 2011，42(suppl 1):895-899. (in Chinese)

[9] Olama M M， Djouadi S M， Papageorgiou I G， et al. Estimation of mobile station position and velocity in multipath wireless networks using the unscented particle filter[C]∥Proceedings of the 46th IEEE Conference on Decision and Control. New Orleans， USA: IEEE， 2007:4590-4595.

[10] Zhang Yiheng， Zhang Hao， Zou Jie. Wireless cooperative localization in the next-generation mobile communication system[J]. Journal of Beijing University of Posts and Telecommunications， 2011，34(1):126-129．

[11] Arasaratnam I， Haykin S. A numerical-integration perspective on Gaussian filters[J]. IEEE Trans on Automatic Control， 2009，54(8):1254-1269.

(责任编辑：刘芳)

An Improved Localization Algorithm in Wireless Sensor Networks Under Complex Background Noise

HOU Jian-jun， ZHU Ming-qiang， LIU Ying

(School of Electronics and Information Engineering， Beijing Jiaotong University， Beijing 100044， China)

To further improve the precision of target localization in the wireless sensor network(WSN), a novel Cubature particle filter algorithm was proposed. Firstly it utilized least square method to estimate the initial target position, the Cubature Kalman filter and Gauss-Newton rule were used to generate more accurate importance density function subsequently by virtue of the measurement updated state variable, which provided proposal distribution for particle filter. The simulation experiment results demonstrate that the proposed algorithm can achieve better locating accuracy and convergence speed under complex background noise, compared with standard PF、 EPF and UPF.

Cubature Kalman filter; particle filter; wireless sensor network; target locating

2014-03-18

国家自然科学基金资助项目(61172130)

侯建军(1957—)，男，教授，博士生导师，E-mail：houjjj@bjtu.edu.cn.

朱明强(1984—)，男，博士生，工程师，E-mail:mqzhu@bjtu.edu.cn.

TN 915.5

A

1001-0645(2016)05-0535-06

10.15918/j.tbit1001-0645.2016.05.018