考虑导引头视场角和落角约束的制导方法

张道驰， 孙静， 温求遒， 夏群利

(1.北京理工大学 宇航学院，北京 100081；2.中国兵器科学研究院，北京 100089)



考虑导引头视场角和落角约束的制导方法

张道驰1， 孙静2， 温求遒1， 夏群利1

(1.北京理工大学 宇航学院，北京 100081；2.中国兵器科学研究院，北京 100089)

针对空地武器采用最优弹道成型制导律进行大落角攻击时易造成导引头跟踪误差角大于其视场角而丢失目标的问题，提出一种满足导弹导引头视场角约束和落角约束的制导方法. 基于线性化模型和小角假设，得到了导引头跟踪误差角的解析表达式，分析了影响导引头跟踪误差角的因素及最大跟踪误差角的取值范围. 在此基础上，针对不同空地武器提出了通过改变末制导初始弹目视线角或放松落角约束的方式满足导引头视场角约束的制导方法，并给出了初始弹目视线角的取值原则及最大允许落角的计算方法. 通过仿真校验，证明了导引头跟踪误差角的解析解的正确性及制导方法的可行性.

视场角约束；落角约束；导引头误差角；空地武器

精确制导弹药通过导引头测量弹轴与弹目线之间的夹角并输出弹目视线角速度信息，导弹利用弹目视线角速度信息采用不同的制导律攻击目标，目标位于导引头视场内是制导弹药实现精确打击的基础. 在对地攻击中，为提高战斗部对目标的毁伤效果，往往需要导弹以较大的落角命中目标，为此许多学者提出了多种大落角制导律[1-5]. 而采用大落角制导律的制导弹药，弹道较为弯曲，弹目交汇过程中极易出现导引头跟踪误差角大于其视场角而丢失跟踪目标的情形，直接影响导弹的命中精度. 因此对于采用大落角制导律的空地武器，需要研究同时满足导引头视场角约束和落角约束的制导方法.

目前国内外针对落角约束和导引头视场角约束的研究很多，Park G B等[6]将视场角约束作为状态不等式约束引入最优制导律求解中，利用最优控制理论得到了含有视场角约束和落角约束的最优制导律. 其本质为一个分段制导律，在导引头误差角小于其视场角时采用最优弹道成型制导律，误差角接近视场角时转为保持导引头最大允许误差角飞行的制导律，在末端导引头跟踪误差角收敛后转为最优弹道成型制导律，制导律切换通过实时求解弹目距离得到. Lee C H等[7]针对捷联导引头跟踪高速目标问题提出了一种保持导引头稳定跟踪目标的混合制导律. 作者利用李雅普诺夫稳定理论得到一种减小导引头跟踪误差角的滑模制导律，将其与比例导引制导律结合，并给出了滑模制导律和比例导引制导律之间的切换逻辑，保证目标始终位于导引头视场内. 顾家立等[8]针对导弹大落角需求引起跟踪误差角超出导引头视场的问题，提出了一种采用开关逻辑的制导律，通过在大落角制导律的基础上引入视线角约束项，当跟踪误差角大于设定阈值后，视线角约束项启动，抑制弹目视线角增大，误差角小于设定阈值后，关闭落角约束. Sang D K等[9]基于视线角速归零推导了等误差角飞行制导律，并给出了保持导引头误差角的制导律切换逻辑，当原导引律使导引头误差角达到导引头视场边界值时，切换到等误差角制导律，当满足误差角收敛条件后，再切换回原导引律. 纵观国内外同时满足导引头视线角约束和落角约束的制导律，均是采用分段制导的原则，通过在大落角制导律的基础上引入不同的指令切换逻辑，当弹目视线角接近导引头视场边界时，引入视线角保护项或采用另一种制导律使目标始终位于导引头视场内. 这种方式破坏了原制导律的最优性，当制导距离较小时将对导弹的命中精度产生很大影响.

本文针对空地武器提出一种新的同时满足导引头视线角约束和落角约束的制导方法. 针对采用最优弹道成型制导律实现大落角攻击的空地武器，首先给出了导引头跟踪误差角的解析解，分析了影响导引头跟踪误差角变化的因素，得到了最大跟踪误差角的取值范围以及取得时刻. 在此基础上，设计了考虑导引头视线角约束的制导方法. 最后通过仿真验证了方法的有效性.

1 问题描述

考虑导弹二维平面内的制导问题，图1给出了弹目交汇运动关系示意图，其中：M为导弹；T为目标；R，q，θ，vm，aM分别为弹目距、目视线角、弹道倾角、导弹速度和导弹过载；qFINS，qFLOS分别为惯性系和初始弹目系下落角约束. 假设导弹飞行中攻角很小可以忽略，则导引头跟踪误差角ε为

(1)

弹目交汇过程中运动方程为

(2)

对式(1)求导可得

(3)

代入式(2)有

(4)

式(4)为一阶微分方程，求解此微分方程可得到弹目交汇过程中导引头跟踪误差角的解析表达式.

2 最优弹道成型制导律下导引头跟踪误差角

文献[10]中推导了最优弹道成型制导律制导指令：

(5)

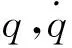
利用线性化模型和小角假设，式(5)可以改写成以终端落角和初始指向误差角表示的形式[10]

(6)

式中：tF为末制导时间；t为当前飞行时间；ε0为初始指向误差角，由式(1)计算得到.

将式(6)代入式(4)并代入R=vr(tF-t)有

(7)

对于静止目标，v=vr，假设导引头跟踪误差角ε较小(ε<15°)，有sinε≈ε，式(7)可简化为

(8)

由初始条件ε(0)=ε0，求解式(8)可得

(9)

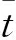
(10)

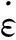
(11)

(12)

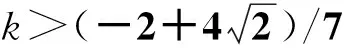
令

(13)

对式(13)中k求导，通过分析可得：

(14)

图2给出了Kεmax与tεmax随k的变化曲线，由曲线可知：随着k的增大，Kεmax先减小后增大，但在k>-0.3时，Kεmax基本维持在0.5附近，表明此时Kεmax对初始条件不敏感. 同时取得最大值时刻也保持在0.5附近，即在末制导中间时刻导引头跟踪误差角达到最大值.

3 满足导引头视场角约束的制导方法

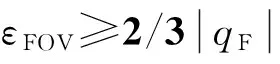
对于空地制导武器，落角约束定义在惯性系下如图1中qFINS，而式(10)落角变化定义在的弹目视线系下，即图1中qFLOS，两者关系为

(15)

本文假设制导初始时刻目标位于导引头视场内，因此只对最大跟踪误差角在制导某一时刻取得情况进行设计. 对最大跟踪误差角在初始时刻取得的条件，其在制导过程中不会丢失目标，本文不做讨论. 将式(15)带入式(12)第2式得导引头最大跟踪最大误差角为

(16)

其中：

由式(16)可知，对于固定落角约束qFINS可以通过选择适当的末制导初始弹目视线角q0，达到减小导引头最大跟踪误差角的目的.

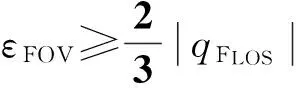
(17)

由以上分析，当初始弹目视线角满足式(17)时，末制导过程中不会出现导引头跟踪误差角大于视场角而丢失目标的情形. 对于有动力的空地制导武器如空地导弹、巡航导弹等，其可以依靠自身动力完成末制导初始位置的调整，使之满足式(17)约束，从而在末制导过程中同时满足落角和导引头视场角约束.

对于无动力空地武器如制导炸弹等，由于动能等约束不能任意调整末制导初始时刻弹目视线角. 为保证命中精度，可以根据导引头视场和初始条件，重新计算最大允许落角，保证末制导过程中导引头不丢失目标. 令末制导过程中导引头最大跟踪误差角等于其视场角，即

(18)

求解式(18)可得

(19)

将式(19)带入式(15)可得到惯性系下最大落角. 式(19)中初始指向误差角ε0和初始弹目视线角q0可以通过弹上导引头和组合导航系统获得，最大允许落角可在制导开始前根据飞行参数实时计算.

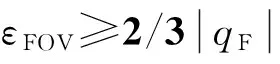
(20)

图3给出了考虑导引头视场角和落角约束的空地武器末制导方法设计流程图.

4 仿真校验

4.1 导引头跟踪误差角验证

式(10)的结果是在线性化模型及小角假设下得到的，为了分析其在非线性大角度下的有效性，假设目标静止不动，不考虑弹体动力学模型，取导弹纵向平面内运动模型为

(21)

弹目交汇运动模型：

(22)

其中：

过载指令ac通过式(5)计算得到.

取导弹速度为vm=250 m/s，初始弹目距离R=3 km，初始弹目视线角q0=0°. 初始指向误差角ε0、落角约束qF及仿真结果如表1所示，图4给出了不同落角约束下导引头跟踪误差角的仿真曲线和理论变化曲线对比图.

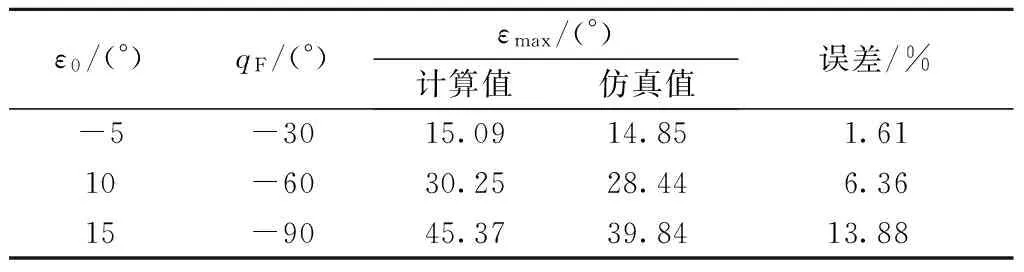
表1 导引头跟踪误差角仿真结果

由图4及表1结果可知，在导引头最大跟踪误差角较小时(<15°)，误差角的理论计算曲线与仿真曲线基本重合，理论计算最大误差角与仿真计算值误差较小(<2%)；在导引头误差角较大时(>15°)，由于不满足小角假设，计算误差较大，但最大误差在15%以内，并且理论计算值大于仿真结果. 因此，式(10)在大的跟踪误差角下仍可作为工程中导引头跟踪误差角的估计及导引头视场角的设计依据.

4.2 考虑导引头视场角和落角约束的制导方法验证

取导引头视场角20°，导弹开始末制导时弹目距离R=3 km，落角约束qF=-70°，由式(17)可知，当初始弹目视线角q0≤-40°时，在任意初始条件下，导引头跟踪误差角均不会大于其视场角.

4.2.1 满足初始弹目视线角约束时仿真结果

取初始弹目视线角q0=-40°，导弹初始位置为

(23)

表2给出了不同初始弹道倾角θ0下的仿真结果，图5、图6给出了导引头跟踪误差角曲线及弹道倾角曲线.

表2 满足初始弹目角约束时不同条件仿真结果

Tab.2 Simulation results satisfied initial line of sight constraints for different initial conditions

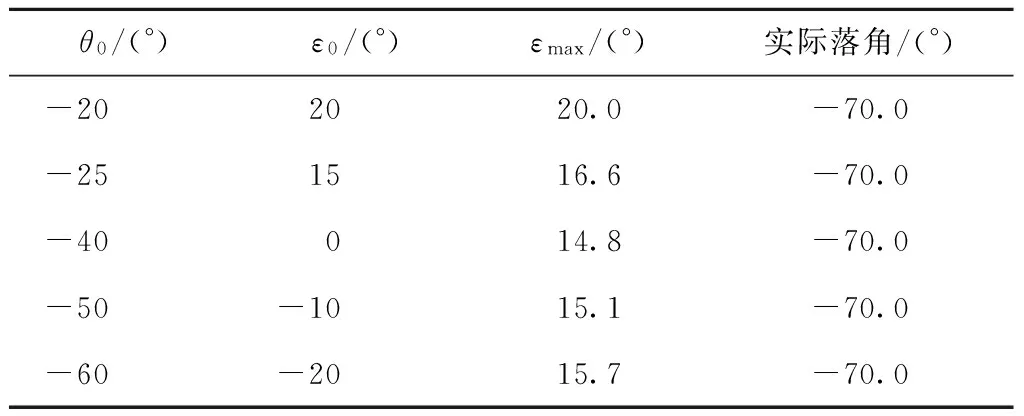
θ0/(°)ε0/(°)εmax/(°)实际落角/(°)-202020.0-70.0-251516.6-70.0-40014.8-70.0-50-1015.1-70.0-60-2015.7-70.0

由图5、图6及表2中仿真结果可知，选择的初始弹目视线角可以在任意初始指向误差条件下满足落角约束和导引头视场角约束. 除初始指向误差角在视场边界情形，导引头跟踪误差角均未达到视场角边界值，此时初始指向误差存在不确定误差不会造成导引头丢失目标.

4.2.2 不满足初始弹目视线角约束时仿真结果

取初始弹目视线角q0=-30°，由于不满足式(17)要求，为保证命中精度，需根据初始指向误差角利用式(19)计算最大允许落角. 表3为不同初始指向误差角的仿真结果，图7～图8为相应仿真曲线.

表3 不满足初始弹目角约束时不同条件仿真结果

Tab.3 Simulation results dissatisfied initial line of sight constraints for different initial conditions

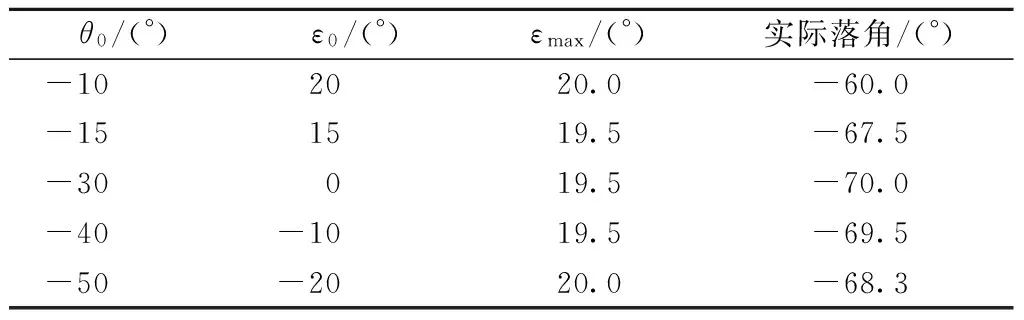
θ0/(°)ε0/(°)εmax/(°)实际落角/(°)-102020.0-60.0-151519.5-67.5-30019.5-70.0-40-1019.5-69.5-50-2020.0-68.3

由表3及图7～图8可知，在不满足初始弹目角约束时，设计的制导方法可以保证导引头在弹目交汇过程中最大跟踪误差角小于导引头视场角，同时尽可能利用最大视场角增大落角.

5 结 论

针对采用最优弹道成型制导律的空地制导武器设计了一种能够满足导引头视场角约束和落角约束的制导方法. 给出了制导过程中导引头跟踪误差角变化的解析表达式，并分析了导引头跟踪误差角的影响因素以及导引头最大跟踪误差角的取值范围. 提出了通过选择适当的初始弹目视线角以减小导引头最大跟踪误差角，或依据导引头视场角和初始制导条件重新计算允许最大落角的制导方法. 通过仿真验证了方法的有效性.

本文结果既可以用于满足导引头的视场角约束和落角约束的末制导设计中，也可以用于末制导导引头跟踪误差角的估计或导引头视场角的设计依据，具有较大的工程应用价值.

[1] Ryoo C K， Cho H， Tahk M J. Optimal guidance laws with terminal impact angle constraint[J]. Journal of Guidance， Control， and Dynamics， 2005，28(4):724-732.

[2] Kim B S， Lee J G， Han H S. Biased PNG law for impact with angular constraint[J]. IEEE Trans Aerospace Electr Syst， 1998，34:277-288.

[3] Ryoo C K， Cho H， Tahk M J. Time-to-go weighted optimal guidance with impact angle constraints[J]. IEEE Transactions on Control Systems Technology， 2006，14(3):483-492．

[4] 刘大卫，夏群利，左媞媞，等.包含弹体动力学的终端角约束弹道成型制导律[J].北京理工大学学报，2013，33(4):363-368.

Liu Dawei， Xia Qunli， Zuo Titi， et al. Trajectory shaping guidance law with terminal impact angle constraint including missile body dynamics[J]. Transactions of Beijing Institute of Technology， 2013，33(4):363-368.(in Chinese)

[5] 王辉，林德福，崔晓曦.一类扩展的弹道成型制导律[J].北京理工大学学报，2014，34(6):597-602．

Wang Hui， Lin Defu， Cui Xiaoxi. Extended trajectory shaping guidance laws[J]. Transactions of Beijing Institute of Technology， 2014，34(6):597-602. (in Chinese)

[6] Park B G， Kim T H， Tahk M J. Optimal impact angle control guidance law considering the seeker’s field-of view limits[J]. Proc IMechE: Part G, J Aerospace Engineering， 2013，227(8):1347-1364．

[7] Lee C H， Hyun C， Lee J G， et al. A hybrid guidance law for a strapdown seeker to maintain lock-on conditions against high speed targets[J]. J Electr Eng Technol， 2013，8(1):190-196．

[8] 顾家立，陈万春.一种带导引头视角和落角约束的导引方法[J].宇航学报，2013，34(6)：782-787．

Gu Jiali， Chen Wanchun. Homing guidance with look angle and impact angle constraints[J]. Journal of Atronautics， 2013，34(6):782-787.(in Chinese)

[9] Sang D K ， Ryoo C K， Tahk M J. A guidance law with a switching logic for maintaining seeker’s lock-on for stationary targets[J]. KSAS International Journal， 2008，9(2):87-97.

[10] Zarchan P. Tactical and strategic missile guidance[C]∥Proceedings of the 6th. Progress in Astronautics and Aeronautics.Reston， USA: AIAA，2012,239.

[11] 刘大卫.侵彻制导炸弹终端多约束最优制导律与弹道研究[D].北京：北京理工大学，2012．

Liu Dawei. Study on the terminal optimal guidance law with multiple constraints and trajectory of penetrating guided bomb[D]. Beijing: Beijing Institute of Technology， 2012. (in Chinese)

(责任编辑：刘雨)

A Guidance Method on Seeker’s Field of View and Impact Angle Constraint

ZHANG Dao-chi1， SUN Jing2， WEN Qiu-qiu1， XIA Qun-li1

(1.School of Aerospace Engineering， Beijing Institute of Technology， Beijing 100081， China;2.Ordnance Science and Research Academy of China， Beijing 100089， China)

A guidance method was proposed, considering seeker field of view constraints and impact angle constraint, for the reason that the seeker look angle of air to ground weapon may overstep the field of view and lose the target when it follows the optimal trajectory shaping guidance law to achieve large impact angle. An analytic expression of seeker look angle was deduced based on the assumption of linearization model and small angle. The factors that influence seeker look angle and the range of maximum seeker look angle were analyzed. On this basis, the guidance method satisfied the seeker field of view constraints through changing the initial line of sight angle or relaxed impact angle constraints was put forward for different air to ground weapons. The select principle of initial line of sight value and the maximum impact angle calculation method were also presented. Numerical simulations verified the effectiveness of the seeker look angle theoretical expressions and the proposed guidance method.

field of view constraint; impact angle constraint; seeker look angle; air to ground weapon

2015-04-21

北京理工大学基础研究基金资助项目(20130142016)

张道驰(1987—)，男，博士生，E-mail:zhangdaochi1988@163.com.

TJ 765.3

A

1001-0645(2016)05-0452-06

10.15918/j.tbit1001-0645.2016.05.003