腹板铺层参数对风力机叶片结构性能的影响

杨瑞， 张志勇， 刘叶垚， 吴卓琦， 王恭喜

(1.兰州理工大学能源与动力工程学院， 兰州730050；2.甘肃省风力机工程技术研究中心， 兰州730050)



腹板铺层参数对风力机叶片结构性能的影响

杨瑞1,2， 张志勇1， 刘叶垚1， 吴卓琦1， 王恭喜1

(1.兰州理工大学能源与动力工程学院， 兰州730050；2.甘肃省风力机工程技术研究中心， 兰州730050)

为研究腹板铺层参数对风力机叶片结构性能的影响。以某1.5 MW水平轴风力机叶片为研究对象，基于有限元分析方法，利用ANSYS软件中梁单元模拟腹板铺层，保持叶片前缘、后缘以及梁帽的铺层形式不变，通过改变腹板铺层角度、顺序和不同铺层角度的层数占整个铺层层数的比例，得到多种研究方案，并对不同方案时的叶片进行模态分析。结果表明：腹板±45°铺层较其他铺层角度能够更好的承受剪切载荷；腹板铺层角度应以±45°为主，且±45°铺层占整个铺层的58%左右时叶片结构性能最好；为了减小各层之间的剪切应力，应避免0°铺层和90°铺层连续铺放。

风力机；叶片；腹板；铺层；模态分析

引言

叶片是风力机捕获风能的关键部件，又是风力机力源、主要承载部件，对整个风力机安全运行起着关键作用[1]。随着风电技术的发展，单机容量增大，叶片也越来越长，腹板对叶片性能的影响也越明显。此外，风场中下游风力机运行过程中受到上游风力机尾流场的影响，同时，由于随机变动的自然大气环境中，风力机叶片的受力情况和运动状况非常复杂[2]，良好的腹板结构对风力机叶片能否正常稳定运行至关重要。大型风力机叶片最主要的的构造形式是由复合材料的上、下翼面及腹板构成。腹板主要由铺层和夹芯材料组成，铺层的角度、顺序、厚度及夹芯材料决定了腹板的性能，合理的腹板铺层能够有效提高叶片的强度和刚度，同时减少叶片质量。为了保证叶片具有足够的可靠性和安全性，对腹板铺层参数与叶片结构性能相互影响机理的研究至关重要。

国内外许多学者对此进行了研究。张兰挺[3]等以距叶根14.6 m的一段为研究对象，研究了铺层参数对风力机叶片静态结构性能的影响。李成良[4]等人利用有限元商用软件ANSYS，选用Shell91和Shell99复合材料壳单元，利用实常数面赋值法定义复合材料铺层结构。廖猜猜[5]等人编程建立了一种风力机叶片约束优化设计模型，以风力机叶片主梁帽的铺层厚度及位置为优化设计变量，合理地设计了主梁帽的铺层厚度。Jensen[6]等人对一个34 m全尺寸复合材料风电机组叶片在挥舞载荷作用下的失效进行了测试分析，对主要承载结构箱型梁进行了全尺寸测试以及非线性有限元计算。李志敏[7]等，基于复合层压板理论和有限元分析方法对大型风力机复合材料叶片铺层设计及结构特性进行了研究。李仁年[8]等人对大型风力机叶片铺层及模态进行了分析，结果显示大型风力机叶片梁帽的铺层对频率及相对位移影响最大。谢少军[9]等基于试验设计法对叶片铺层结构进行研究，得出0°纤维铺层与±45°铺层对强度的影响存在耦合作用，但是该方法工作量大。冯消冰[10-13]以工程常用铺层角度为基础，采用遗传算法对复合纤维风机叶片根部及整体进行铺层优化设计。在目前的研究中，以腹板铺层参数为研究对象的相对较少。

本文利用复合材料有限元法，针对某1.5 MW风力机叶片，基于ANSYS有限元分析软件，研究分析腹板铺层参数与叶片结构性能相互影响机理，从而为叶片腹板铺层结构设计提供研究基础。

1 叶片有限元模型

以某1.5 MW单腹板水平轴风力机叶片为研究对象。叶片长度40.5 m，风轮直径83 m，最大弦长3.1 98 m，额定转速17.3 2 r/min。叶片各截面参数见表1。

表1 叶片各截面参数

不考虑腹板位置对叶片性能的影响，运用ANSYS有限元分析软件，基于APDL语言建立不同方案时叶片的参数化模型，如图1 所示。图2 为叶片截面,其中A3356、A162为梁帽，A316为前缘，A287为后缘，A7为腹板。

图1 叶片有限元模型

图2 叶片截面

2 模态分析

模态分析用于确定机械部件的振动特征，即结构的固有频率和振型，是结构承受动态载荷设计中的重要参数[14]。结构整体的动力学平衡方程为：

Mu″+Cu′+Ku=F(t)

(1)

式中：M为质量矩阵，C为阻尼矩阵，K为刚度矩阵，u、u′和u″分别为结构整体各节点的位移向量、速度向量和加速度向量，F为结构整体的外载荷向量。无阻尼模态分析是假设没有阻尼和外力作用，则式(1)变为：

Mu″+Ku=0

(2)

对于线性系统，式(2)解的形式为：

u=φicosωit

(3)

式中：φi为第i阶模态对应的振型特征向量，ωi为第i阶模态的固有频率，rad/s，t为时间。对风力机叶片，腹板铺层将影响叶片结构的刚度矩阵K和质量矩阵M。腹板铺层的改变最终影响叶片结构频率和叶片整体刚度特性发生变化。

3 铺层方案

确定腹板铺层需考虑的主要原则是：材料铺层能够满足叶片刚度、强度的同时质量最轻，且成型工艺简单，成本低[15]。叶片腹板的主要作用是抗剪切，其铺层的好坏直接影响到叶片结构的动力学特性。ANSYS软件中主要选择壳单元SHELL99、SHELL91、SHELL181、SHELL190用于复合材料结构建模[16]。本文在模拟计算叶片前缘、后缘及梁帽时选用SHELL181壳单元，腹板选用BEAM188梁单元。为提高风力机叶片整体刚性和稳定性，腹板单元铺层采用对称形式，不考虑材料对腹板性能的影响，中间层夹芯材料选用PVC泡沫板，其两侧选择玻纤/环氧材料。为了更好地研究腹板铺层参数与风力机叶片的影响机理，铺层都选用单轴向布。单元铺层如图3 所示。

图3 叶片单元铺层图

图3中材料1为玻纤/环氧材料，厚度为0.015 m，中间夹层2为PVC，厚度为0.2 5 m，其两侧对称铺层，腹板总共铺层为25层，图中只显示了中间7到19层。其中PVC泡沫材料力学性能：弹性模量E=8.3 0×107Pa，剪切模量G=1.6 ×106Pa，泊松比μ=0.3 8，密度ρ=83.0 kg·m-3。玻璃/环氧的单层力学性能为：

EX=38.6gPa，EY=8.2 7 GPa

EZ=8.2 7 GPa，PRXY=0.2 6 GPa

PRYZ=0.2 6 GPa，PRXZ=0.01 GPa

GXY=4.1 4 GPa，GYZ=1.6 6 GPa

GXZ=4.1 4 GPa，ρ=1800 kg/m3

文中腹板铺层[α°/β°/γ°]T表示铺设角依次为α°、β°、γ°，且各层厚度相同，下标T表示循环铺层次数；±β°表示依次铺设β°和-β°。铺层方案见表2。不同铺层比例时的方案见表3。

表2 铺层方案

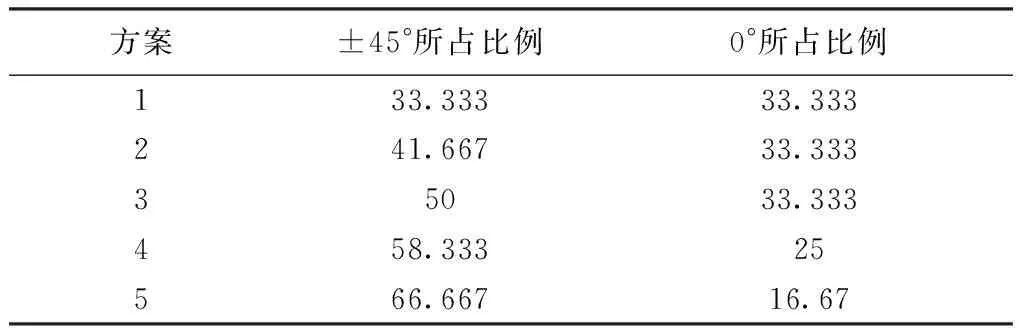
表3 不同铺层比例时的方案

由于腹板中间夹层PVC两侧对称铺层，所以表1中只列出PVC一侧的铺层方案。最后通过meshing功能将铺层信息和材料属性分配给所对应的面，然后划分有限元网格；将叶片视为一个变截面悬臂梁，对其加载只有根部零位移约束，分别对不同方案时的叶片进行求解分析。

4 结果分析

根据叶片振动理论，风轮旋转过程中，风轮振动的能量主要集中在前二阶模态振型，而叶片的高阶固有频率只有在叶轮高转速下才会被激发，所以本文只针对叶片前二阶模态振型特性进行阐述。规定叶片的最大变形量占叶片总长的百分数为相对变形，作图分析。

4.1 不同铺层角度

图4(a)、(b)分别为叶片一、二阶振型所对应的频率，相对位移以及最大等效应力，由图4(a)可知。方案1在一阶频率、相对变形以及最大等效应力上较方案2变化不大。方案3时叶片的一阶频率、相对变形以及最大等效应力为最大。由图4(b)可知。方案1在二阶频率和相对变形上相对方案2变化不大，但方案2的最大等效应力有所增加；方案3时叶片二阶频率和相对变形最大，而最大等效应力最小。

图4叶片频率、相对变形以及最大等效应力

对比分析图4(a)、(b)可知，方案3对叶片动态性能影响较明显，这主要是因为方案3时，腹板为±45°铺层，而腹板的作用主要是抗剪切，±45°铺层能够更好的承受剪切载荷，所以其对叶片性能影响较明显。实际工程运用中，腹板铺层应以±45°为主。

方案3时，一、二阶振型所对应叶片压力面的等效应力分布如图5所示，图中应力单位为MPa。由图5可知，一阶时叶片压力面的等效应力较大，主要集中在叶根和叶片的2/3段，而二阶时主要集中在叶根和距叶根2/3叶片处。这主要是因为振型不同。实际腹板铺层时，应对应力集中的部位进行加强处理。

图5等效应力分布

图6为方案3叶片的前八阶模态振型。由图6可知，叶片的振型不受腹板铺层参数的影响，一阶模态振型为挥舞振动；二阶模态振型为摆振振动；三阶模态振型为挥舞振动和摆振振动的耦合；从五阶模态开始，可以明显看出，有扭转振动。由振动理论可知，叶片的振动主要以一阶振动为主，即弯曲振动为主。

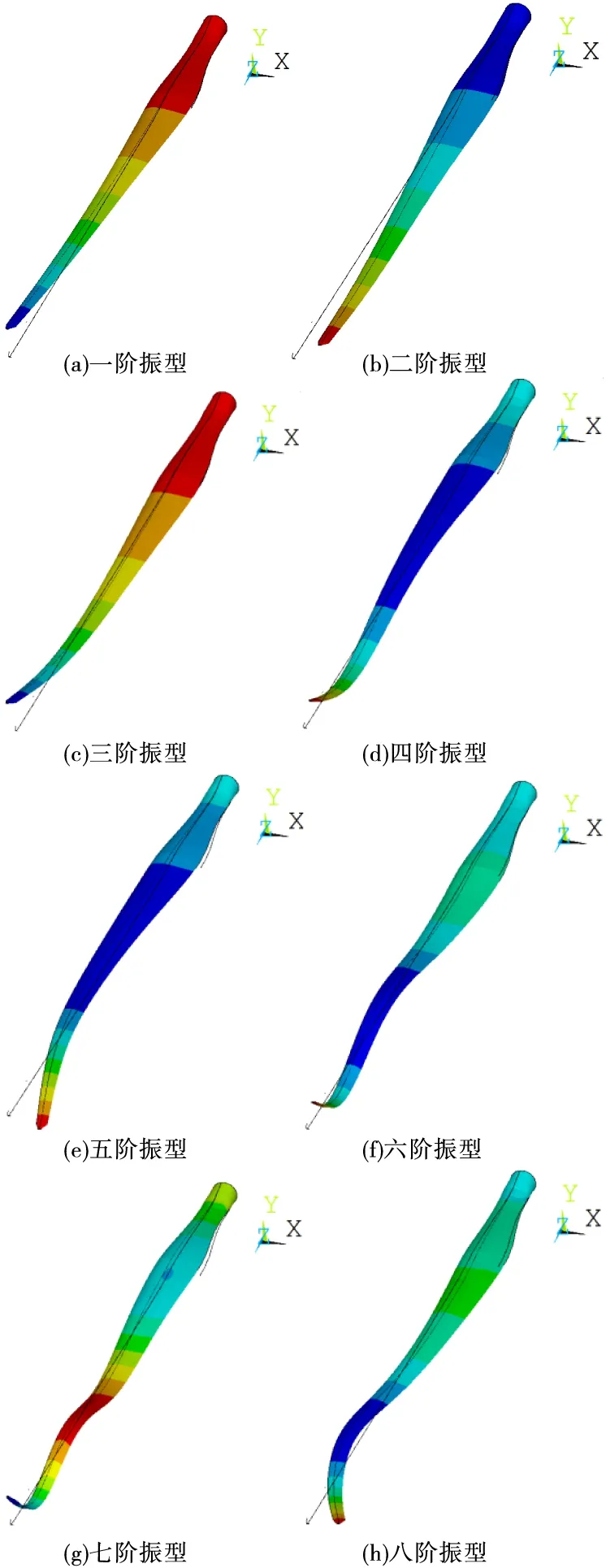
图6叶片的前八阶模态振型

实际工程应用中，叶片的固有频率应远离风轮的旋转频率和整机固有频率。以防止风力机叶片发生共振，对风力机造成破坏。

4.2 不同铺层顺序

图7(a)为一阶模态所对应的频率、相对变形以及最大等效应力，由图7(a)可知，方案5的一阶频率和最大等效应力最大，方案1的相对变形量最小，而方案2、3、4、5的相对变形几乎保持不变；方案3的最大等效应力较方案1、2、4有所增大而小于方案5的。图7(b)为二阶模态所对应的频率、相对变形以及最大等效应力，由图7(b)可知，方案1、2、3、4二阶频率和最大等效应力基本保持不变；方案5对二阶频率最大，而最大等效应力最小。

图7不同方案时一、二阶振型所对应叶片频率、相对变形以及最大等效应力

对比图7(a)、(b)可知，方案5对叶片性能影响最大。这主要是因为方案5的0°和90°分割铺放，减小了各层之间的剪切应力。腹板铺层时应将0°和90°分隔铺放。

4.3 不同铺层比例

由图8(a)可知，方案1、2、3、4的一阶频率逐渐减小；方案4时达到最小值0.3 283 Hz；方案5的一阶频率较方案4有所增加，但小于方案1、2、3的；方案4的相对变形最小，为2.1 %；方案1、2、3、5的相对变形相差不大；方案2的最大等效应力较方案1和3时稍有减小；方案4时，最大等效应力最小，为15.8 kPa；方案5的最大等效应力达到最大，为21.1 kPa。由图8(b)可知，方案1较方案2和方案5的二阶频率、相对变形以及最大等效应力变化不大；方案3的二阶频率较方案2有所增加，而最大等效应力相对减小；方案4时二阶频率达到最大，为0.785 Hz，而相对变形和最大等效应力最小，分别为1.88%和53 kPa。

图8不同方案时一、二阶振型所对应叶片频率、相对变形以及最大等效应力

对比分析图8(a)、(b)可知，方案4对叶片性能影响较大，一、二阶振型时，方案4的最大等效应力和相对变形都最小，有利于风力机叶片运行，实际腹板铺层时，±45°铺层占腹板铺层的58%左右。

5 结论

基于ANSYS有限元软件，建立1.5 MW单腹板水平轴风力机叶片模型，分析了不同腹板铺层参数时叶片的模态性能，(包括频率、相对变形、最大等效应力)，通过对比不同腹板铺层方案下的模态分析可得出以下结论：

(1)腹板不同铺层角度时，±45°铺层较其他角度能够更好的承受剪切载荷。实际工程运用中，腹板铺层应以±45°为主。

(2)叶片的振型不受腹板铺层参数的影响；振型不同时，应力分布不同，叶片应力主要集中在叶根处和叶片的2/3段处，腹板铺层设计时，对该部位进行加强处理。

(3)为了减小各层之间的剪切应力，腹板铺层时应避免0°铺层和90°铺层连续铺放。

(4)为了风力机叶片可靠运行，实际腹板铺层时，±45°铺层占腹板铺层的58%左右。

本文研究了腹板铺层参数与风力机叶片结构性能之间的相互影响机理，有利于叶片结构设计时确定合理的腹板铺层，增强腹板抗剪切能力，提高叶片整体刚性和运行时的稳定性，防止震动破坏。对实际工程中风力机叶片腹板铺层设计和安全运行和提供一定的参考。但文中铺层都选用单轴向布，实际工程运用中，在保证满足腹板性能要求的前提下，如能用多轴向布替代相应角度单轴向布的连续铺设，则可减少铺放次数、提高效率、降低成本。

[1] 胡燕平,戴巨川,刘德顺.大型风力机叶片研究现状与发展趋势[J].机械工程报,2013,49(20):1311-151.

[2] 李媛.风力机叶片流固耦合数值模拟[D].北京:华北电力大学,2011.

[3] 张兰挺,邓海龙,郜佳佳,等.铺层参数对风力机叶片静态结构性能的影响分析[J].太阳能学报,2014,36(6):1059-1064.

[4] 李成良,王继辉,薛忠民,等.基于ANSYS 的大型风机叶片建模研究[J].玻璃钢/复合材料,2009(2):52-55.

[5] 廖猜猜,赵晓路,王建礼,等.基于风力机叶片铺层的频率优化设计[J].工程热物理学报,2011,32(8):1311-1314.

[6] JENSEN F M,FALZON BG,ANKERSCN J,et al.Structural testing and numerical simulation of a 34 m composite wind turbine blade[J].Composite Structures, 2006,76(1):52-61.

[7] 李志敏,李春,高伟,等.大型风力机复合材料叶片铺层设计及结构特性研究[J].现代制造工程,2014,3(6):5-9.

[8] 李仁年,刘有亮.大型风力机叶片铺层及模态分析[J].太阳能学报,2015,36(1):49-53.

[9] 谢少军,潘柏松.基亍实验设计法的风机叶片铺层结构分析及优化[J].机电工程,2012,29(2):159-162.

[10] 冯消冰,黄海,王伟.大型风机复合材料叶片铺层优化设计[J].玻璃钢/复合材料,2013,5(3):3-7.

[11] 冯消冰,黄海,王伟.基亍遗传算法的大型风机复合材料叶片根部强度优化设计[J].复合材料学报,2012,29(5):196-202.

[12] 潘柏松,谢少军,梁利华.风力机叶片叶根复合材料铺层强度特性研究[J].太阳能学报,2012,33(5):769-775.

[13] SODEN P D,HINTON M J,KADDOUR A S.Recommendations for designers and researchers resulting from the world-wide failure exercise[J].Composites Science and Technology,2004,64(3-4):589-604.

[14] 赵晶,王世杰.ANSYS有限元分析应用教程[M].北京:冶金工业出版社,2014.

[15] 魏远,李春,李志敏.风力机复合材料叶片内部结构典型铺层及分析[J].能源研究与信息,2013,29(3):179-184.

[16] 马志勇.大型风电叶片结构设计方法研究[D].北京:华北电力大学,2011.

The Effect of the Beam Ply Parameters on Structure Performance of Wind Turbine Blade

YANGRui1,2,ZHANGZhiyong1,LIUYeyao1,WUZhuoqi1,WANGGongxi1

(1.College of Energy and Power Engineering, Lanzhou University of Technology, Lanzhou 730050,China;2.Wind Energy Technology Research Center of Gansu Province, Lanzhou 730050,China)

The effect of the beam ply parameters on structure performance of wind turbine blade has been studied.Based on the finite element method,a 1.5 MW horizontal axis wind turbine blade was chosen as the research object.Beam ply was simulatedby using beam element in ANSYS software.Keeping the ply form of blade leading edge, trailing edge and the cap,a variety of research plansweregottenby changing the angle and order of beam ply or the proportion of layer number of different ply angle in whole layer number.Modal analysis was carried out on the blades of different solutions.The results show that the beam with plus or minus 45° ply will be able to bear shearing load better than other ply angle.Ply angle should be given priority to theuseof plus or minus 45°.The blade structure performance is best when plus or minus 45° ply accounts for around 58% of the whole ply.In order to reduce shear stress between the layers, 0° ply and 90° layer continuous plyshould be avoided.

wind turbine;blade; beam; ply; modal analysis

2016-07-15

国家自然科学基金(11162009)

杨 瑞(1970-)，男，河南夏邑人，教授，博士，主要从事风力机气动特性及结构方面的研究，(E-mail)1694794148@qq.com

1673-1549(2016)05-0027-06

10.11863/j.suse.2 016.05.07

TK83

A