灰色-BP神经网络在深基坑变形预测中的应用研究

黄永红

(重庆市勘测院， 重庆400020)



灰色-BP神经网络在深基坑变形预测中的应用研究

黄永红

(重庆市勘测院， 重庆400020)

随着城市化进程的推进，向地下空间发展将是趋势，由此带来大量深基坑工程。深基坑的稳定问题不仅关系上部结构的安全，而且还会影响周边建筑物的变形，因此深基坑变形研究越来越受到重视。将改进灰色预测模型与BP神经网络组合模型结合，通过在南京某大型深基坑的变形模拟和预测效果对比，改进后的灰色模型在一定程度上提高了拟合精度与预测精度，而灰色-BP组合模型在此基础上通过MATLAB平台又进一步地提高了拟合与预测的精度。该研究可为工程施工提供较好的指导意义，并为同类工程提供借鉴。

灰色-BP神经网络；深基坑；变形预测

引言

随着地下空间项目在我国的快速发展，大量的深基坑工程越来越影响人们的日常生活，在深基坑的稳定性不足容易导致附近建筑物的倾斜，上部结构的变形破坏等问题。目前，国内外对深基坑变形规律的研究尚不成熟。工程中较常用的方法是根据施工动态的监测数据对沉降值进行推算，以期提高预测的精度[1-3]。然而，对于饱和土而言，结合大量的观测实例可以看出，根据双曲线预测的结果往往会偏大，而指数曲线法进行预测得到的结果往往偏小[4-5]。另外，灰色理论也受限于非等时距，以及观测值累加生成不具有指数规律等情况[6-8]。目前，随着计算机技术的普遍应用，结合计算机软件研究地表沉降规律已成为趋势，将提升研究效率，有效提高预测精度[9]。本文结合Matlab软件，通过建立灰色-BP神经网络方法，对南京市某过江隧道和匝道的深基坑工程中CX03点的变形趋势进行短期预测。

1 初始边值改进的灰色预测模型

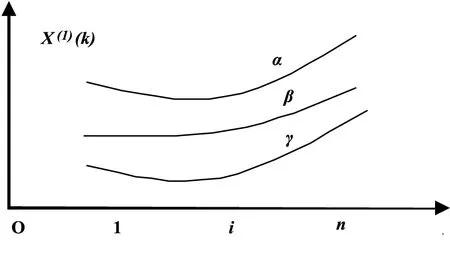
图1 拟合曲线分析

无论选择k=i(i=1,2,3…n)点作为迭代的基准都会出现类似情况，不一样的是灰色模型对信息新旧较为敏感，选择新的序列值，可以使误差减少[11]。通过调整边值(灰色GM(1,1)模型的初始条件)，对该模型进行优化改进成新的GM(1,1)。

考虑边值问题的预测模型方程组[8]：

(1)

通过分析灰色模型边值的响应表达式可以看出生成序列的预测值与原序列号的预测值的边值条件有关。基于此，可将方程组改进为：

(2)

其中，δ是对x(0)(1)的修正量。修正后离散时间响应式为：

(3)

(4)

整理得

(5)

(6)

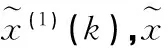
(7)

e-a(k-1)-x(0)(k)]·e-a(k-1)}=

e-2a(k-1)-x(0)(k)]·e-a(k-1)+

(8)

令φ`(δ)=0，得：

(9)

2 BP神经网络模型的结构设计

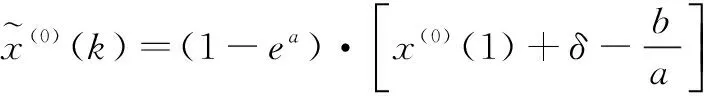
BP神经网络计算：

(1)设输入的信息向量：

X=(x1,x2,···,xn)T

(10)

那么与之对应的输出信息向量为：

Y=(y1,2,···,yn)T

(11)

(2)设隐含层的神经元各输入量为：

(12)

式中：j=1,2,….,k,…,n，Wij表示输入层神经元与输出层神经元之间的权值大小，θj称之某个神经元隐含层的阀值，k为隐含层单元的数量。

(3)这里激活函数采取Sigmoid函数：

(13)

隐含层输出为：

(14)

各神经元输入层输入为：

(15)

各神经元输出层为：

(16)

式中：t=1,2,…,p,…,wjt为隐含层神经元与输出层神经元之间的权值大小，λt为输出层神经元的阈值。

采用平方误差函数计算在误差反传过程中单个样本误差Ek，

(17)

该网络模型总误差为：

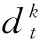
网络进行学习的目的就是使得Ek降为最小，一般典型优化的计算方法都是采取一阶梯度法，也称之为最速下降法。此方法关键在于寻找某个目标函数E关于寻优参数的一阶导数。从输出层开始进行计算并逐层求解E对各个权值的导数，令：

(18)

η称之为学习效率。

修正权值：

(19)

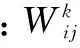
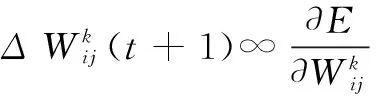
输出层：

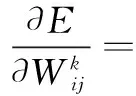
(20)

式中：

(21)

Q-1层即隐含层时：

(22)

式中：

(23)

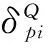
通过以上方法可以对隐含层、输出层的连接权值与阀值进行调整，对网络模型进行一次完整的训练。

3 改进的灰色模型与BP神经网络组合预测模型

采用改进后的灰色系统与神经网络模型组合模型，首先使用基于初始边值和背景值生产方式改进得到的GM(1,1)进行预测，之后采用改进后的灰色模型预测结果代替BP神经网络的输入样本值，采用实际测量得到的基坑数据作为模型的样本值，通过训练BP神经网络，得出用于预测基坑变形的神经网络模型，其具体的建模步骤如下：

(1)将实测数据应用在改进后的灰色模型中。

(2)将改进后的灰色模型得到的预测数据作为BP神经网络的输入值，将对应的实测值作为对比的输出向量的目标值，对BP神经网络进行归一化处理分析。

(3)当输出的值不满足期望输出目标值时，反向传播修改权等直到得到满意的仿真结果，所得到的仿真结果即为此组合模型预测的结果。

组合模型具体运算编程步骤如图2 所示。

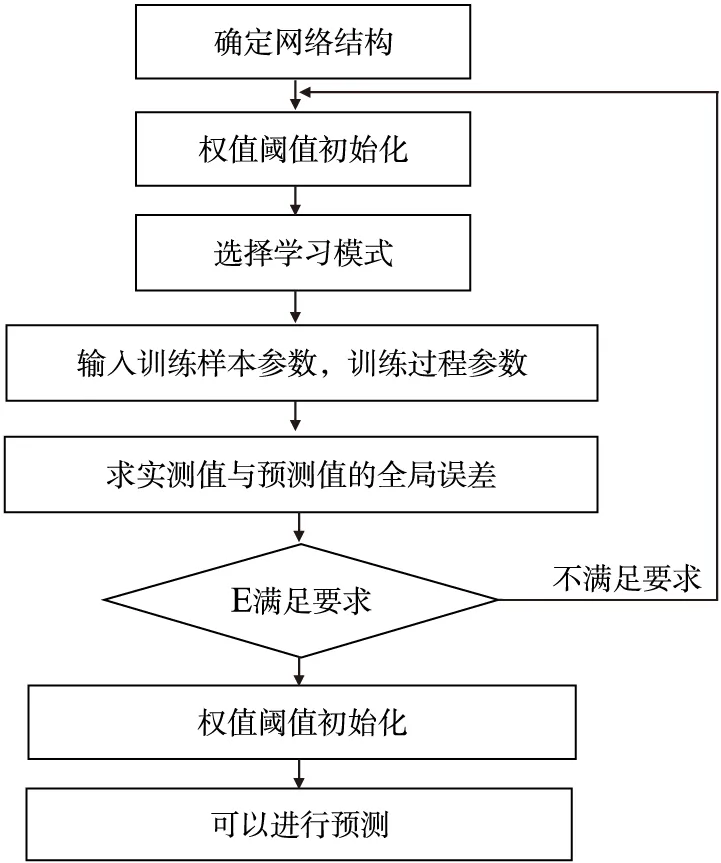
图2 组合模型运算流程图

4 算例分析

深基坑工程是一项特别重要而且复杂的工程，在施工过程中，如果发生事故容易造成人员和财产的损失，所以为了保证基坑开挖过程中支护结构和周边建筑物的安全，必须对深基坑的侧壁与周围环境制定支撑、加固及保护措施，并制定详细的监测方案，根据监测数据调整施工方法与进度。本文以南京市某过江隧道和匝道的深基坑工程中CX03点的监测数据为例，通过MATLAB计算软件，采用本文建立的灰色-BP神经网络方法预测变形趋势。

原序列：

X(0)={2.6 2,3.6 0,4.3 6,5.02,5.5 8,5.96,6.4 8,

8.4 0,9.90,9.6 8,9.88,9.90}

原序列紧邻累加序列：

X(1)={2.6 2,6.2 2,10.5 8,15.6 ,21.1 8,27.1 4,

33.6 2,42.02,51.92,61.6 ,71.4 8,81.3 8}

传统灰色GM(1,1)模型：

(24)

边值改进模型：

-0.5

(25)

背景值优化模型：

(26)

(27)

N=n-1

(28)

(29)

(30)

41.5 2e0.096(k-1)-38.5 ,k∈[1,n]

(31)

基于背景优化的边值改进模型：

41.5 2e0.096(k-1)-38.5 -0.5 e0.096(k-1)=

41.02e0.096(k-1)-38.5

(32)

相对误差：

(33)

或

表1 为使用基于初始边值和背景值生产方式改进得到的GM(1,1)进行预测，然后采用改进后的灰色模型预测结果代替BP神经网络的输入样本值，得出用于预测基坑变形的神经网络模型。对比表1 、2可知其相对误差最大值由原来表2 的18.3 1%，降为表1 的5.01%，图3 采用坐标图的形式直观表现了表1 、表2 的拟合值，通过对比可知改进的灰色-BP组合模型明显提高了拟合与预测的精度。

5 结束语

通过改进灰色预测模型与BP神经网络组合模型在

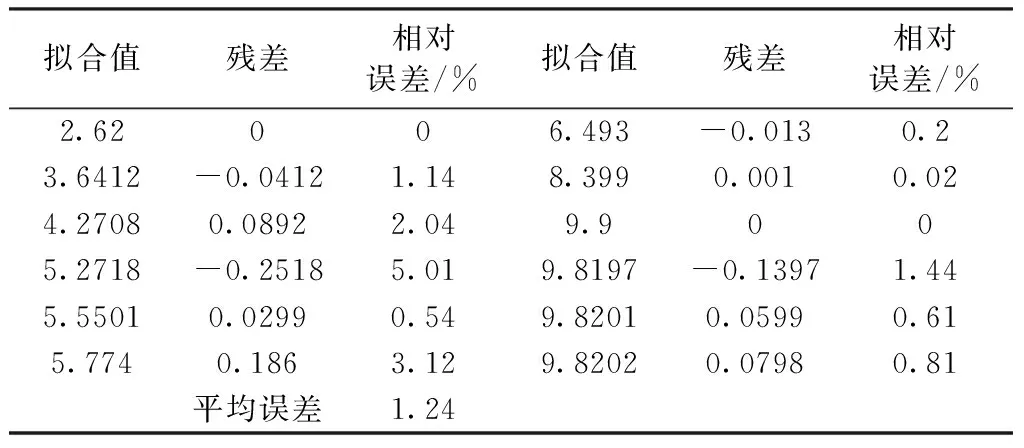
表1 组合模型误差表

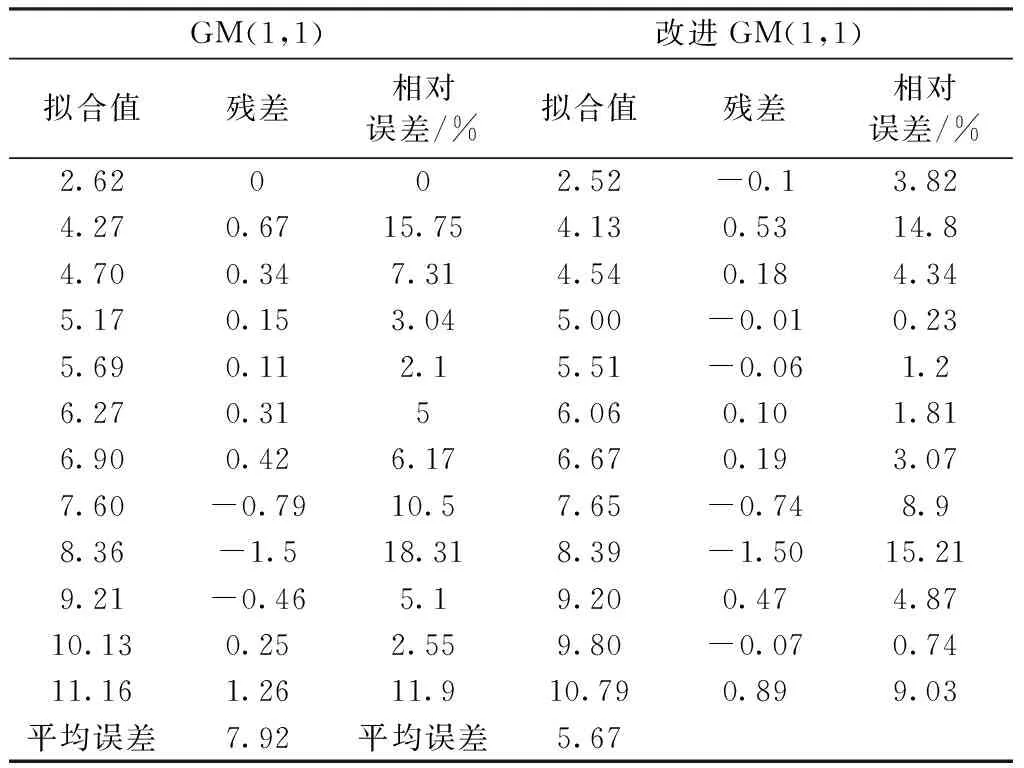
表2 GM(1,1)与改进的GM(1,1)模型预测

图3 实测和预测值对比图

南京某大型深基坑的变形模拟和预测效果对比，改进后的灰色模型在一定程度上提高了拟合精度与预测精度，而灰色-BP组合模型在此基础上通过MATLAB平台又进一步地提高了拟合与预测的精度。在展现灰色-BP组合模型优势的同时，又展现了BP神经网络模型在非线性及函数模拟等方面的优势，该模型结果显示优化的组合模型对深基坑变形预测有更高的精度。基于改进灰色-BP组合模型预测系统的建立以及应用具有一定的指导意义。

[1] 徐鑫鑫,苏华友,张春萍.BP神经网络在基坑周边地表短期沉降预测中的应用[J].四川理工学院学报:自然科学版,2013,26(2):53-56.

[2] 彭涛,杨岸英,梁杏.BP神经网络-灰色系统联合模型预测软基沉降量[J].岩土力学,2005,26(11):1810-1814.

[3] 秦艳华.基于FOA优化BP神经网络的电子商务网站评价研究[J].四川理工学院学报:自然科学版,2015,28(6):36-41.

[4] 王玉雯.昆明深基坑变形监测与预测的应用研究[D].昆明:昆明理工大学,2011.

[5] 刘安宁,来庆专,吴瑞刚,等.深基坑上部土钉墙土钉轴力监测及分析[J].四川理工学院学报:自然科学版,2015,28(1):59-62.

[6] 张德丰.MATLAB 神经网络应用设计[M].北京:机械工业出版社,2009.

[7] ROBERT H N.Theory of the back propagationneural network[C]//Harry Wechsler.Proceedings ofInternational Joint Conference on Neural Networks,Orlando, Florida,USA,February 1-5,1992:65-93.

[8] 房亚群,吴一凡.测量不确定度的BP神经网络模型[J].四川理工学院学报:自然科学版,2015,28(4):22-26.

[9] 张乐.地铁隧道施工地表沉降预测模型及实证研究[D].武汉:华中科技大学,2011.

[10] 齐干.基于BP 网络的深基坑变形预测研究[D].桂林:桂林工学院,2004.

[11] 余江,陶宇.BP神经网络和灰色系统预测模型在深基坑地表沉降中的应用[J].浙江水利科技,2010(3):80-82.

[12] 罗毅,姚毅,李莺,等.基于BP 神经网络的输电线路覆冰增长模型研究[J].四川理工学院学报:自然科学版,2012,25(1):63-66.

[13] 傅荟璇,赵红.MATLAB 神经网络应用设计[M].北京:机械工业出版社,2010.

[14] 贾萍,方源敏,卢水牯.Logistic 模型在高层建筑沉降监测中的应用[J].河南科学,2011,29(3):329-332.

[15] 刘彩红.BP神经网络学习算法的研究[D].重庆:重庆师范大学,2008.

[16] 杨赛.BP神经网络学习问题的分析研究[D].赣州:江西理工大学,2010.

[17] 李晓峰,徐玖平,王荫清,等.BP人工神经网络自适应学习算法的建立及其应用[J].系统工程理论与实践,2004(5):1-8.

Study on Application of Gray-BP Neural Network to Deformation Prediction of Deep Foundation Pit

HUANGYonghong

(Chongqing Survey Institute, Chongqing 400020, China)

With the advance of the urbanization process, more and more underground space was developed, which brings a lot of deep foundation pit engineering. The stability of deep foundation pit is not only related to the safety of the upper structure, but also affects the deformation of the surrounding buildings, so the research of the deformation of deep foundation pit is more and more important. The combination of grey prediction model and BP neural network combination model is improved. by comparing the deformation simulation and prediction effect of a large deep foundation pit in Nanjing, it is shown that the improved grey model improves the precision of fitting and forecasting in a certain extent, based on which the grey-BP combination model through MATLAB platform further improves the precision of fitting and prediction. This research can provide a good guide for engineering construction, and provide reference for similar projects.

grey-BP neural network; deep foundation pit; deformation prediction

2016-04-19

黄永红(1966-)，男，重庆合川人，副教授，主要从事地下空间方面的研究，(E-mail)yonghong2016yh@163.com

1673-1549(2016)05-0018-05

10.11863/j.suse.2 016.05.05

TU473

A