极坐标法测设曲线及误差分析

张 瑞 花

(太原晋万通公路勘察设计有限公司，山西 太原 030006)



·测量·

极坐标法测设曲线及误差分析

张 瑞 花

(太原晋万通公路勘察设计有限公司，山西 太原 030006)

通过对控制测量成果的分析，提出了曲线交点坐标在同一假定坐标系下的求解方法，并阐述了极坐标法在曲线测设中的应用，对放样误差作了研究，以供参考。

极坐标法，曲线，交点坐标，放样误差

0 引言

传统意义上的任意点极坐标法测设曲线，曲线的坐标系大都是以ZH(或HZ)为坐标原点，切线方向为坐标x轴建立起来的，这样的坐标系对于一条曲线来讲，ZH一侧的坐标系与HZ一侧的坐标系需要平移，才能转化为同一坐标系统；并且相邻的曲线坐标系都是相互独立的，没有联系。所谓的任意点置镜，也指是在放样时，临时置镜曲线上某一已知点(如ZH或HZ)，后视一已知点(如JD)，然后再任意找一点P，测出夹角以及距离，从而确立以点P为原点，P-ZH方向为一坐标轴的坐标系统，再置镜P点，后视ZH测设曲线。这样临时确定的坐标系统及基准测点P精度很低。

如果能够将线路中线上的点纳入导线控制网的坐标系统中，那么，所有的直线和曲线都将与导线网产生联系。为此，我们只需在平面控制测量中做一些工作，然后通过对控制测量成果做一些数学解算，即可将线路中线纳入导线网络中。

1 交点坐标的解算

1)导线的布设。导线沿线路走向直伸布设，边长尽可能长。线路每条直线上的转点(即切线方向上的点)至少有两个作为导线点。

2)转向角的获得和曲线要素的重新计算。控制测量完成后，经过平差，得到了每条曲线两端直线(在切线方向上)点的坐标。根据这些坐标值反算得到两条直线的坐标方位角，两方位角相减，得到了精测的转向角α，它的精度较定测时的转向角精确得多。由于精测得到的转向角与定测有一定的差异，那么曲线的部分要素也发生了变化。在定测时，曲线要素是查表计算的，只精确到厘米，为了使曲线要素与导线网的精度相匹配，需重新计算曲线要素。

3)计算交点坐标。根据平面控制测量的成果，每条曲线两端切线方向上至少有两个点坐标值已知，根据两点确定一条直线的定理，这两条直线可分别表示为一次函数y1=k1x1+b1，y2=k2x2+b2；又根据交点的定义可知，这两条直线在交点处有一组公共解。令y1=y2，x1=x2，通过解二元一次方程组，得到的这个公共解即为交点的坐标(x，y)。

示例：已知某线某段JD135-2曲线两端切线方向上的点的坐标，如图1所示：控制测量成果中，直线上转点的坐标为：ZD135-1(3 359.817 9，-121.880 0);ZD135-2(3 857.693 0，-75.832 5);ZD135-3(4 222.188，-7.169);ZD135-4(4 241.251，1.768)。

交点坐标的求解。

1)根据一次函数的定义，直线ZD135-1～ZD135-2可表示为：

x1=k1y1+b1。

将上述ZD135-1，ZD135-2两个点的坐标值代入，得到两个二元一次方程：

解以k1，b1为未知数的二元一次方程组，得:

k1=10.812 2。

b1=4 677.609 7。

x1=10.812 2y1+4 677.609 7(直线x1的表达式)

2)同理：x2=k2y2+b2。

x2=2.133y2+4 237.479 8(直线x2的表达式)。

3)在交点处，x2=x1=x，y2=y1=y。

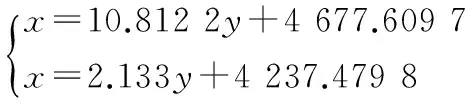
解二元一次方程组，得:

y=-50.711。

x=4 129.313。

交点的坐标为：JD135-2(4 129.313，-50.711)。

2 曲线上点的坐标计算程序(CASIO·fx-4500P计算器)

1)程序概述。本程序可以完成缓和曲线、圆曲线上任意点的坐标计算。控制测量完成后，所有曲线上的点都纳入了导线网这一坐标系统，通过解方程组可以得出所有曲线的交点坐标以及相邻两交点间夹直线(在切线方向上)的坐标方位角，然后根据导线坐标增量的计算方法，计算出任意一点的坐标。

2)数学模型。坐标计算程序见表1，表2。

3)标识符及变量意义说明：XJD,YJD均为该曲线交点的坐标；R为圆曲线半径；L0为缓和曲线长；T为切线长；L为曲线上任意一点至ZH(或HZ)的弧长；U为交点到曲线中线点在切线上投影点的坐标方位角；V为投影到曲线中线点的坐标方位角。

程序中，共有8个变量，但对于同一条曲线而言，在重复执行过程中，变化的量只有弧长L一个。在计算QZ点另一侧的坐标时，U，V也将变化。

表1 坐标计算程序Ⅰ(缓和曲线)

表2 坐标计算程序Ⅱ(圆曲线)

3 极坐标法在曲线测设中的应用

置镜已知控制点A，后视另一已知控制点B，预置已知坐标方位角αA～B，则置镜点至待测点P的方位角和距离为：

αA～P=tan-1(YP-YA)/(XP-XA)(得出角度后判别象限)；

DAP=[(XA-XP)2+(YA-YP)2]1/2。

一般程序计算器中，都有直角坐标与极坐标转化功能，按反算键SHIFT POL得出的角度即为方位角。

4 精度分析

放样误差。极坐标法放样，不论是一般点位，还是曲线测设，都是通过方位角和距离完成的，即：

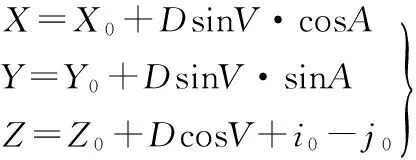
其中，X0,Y0,Z0均为测站坐标；i0,j0分别为仪器高、棱镜高。

对上式微分并转换成中误差后，得：

D2cos2Vcos2A(mV/ρ)2+D2sin2Vsin2A(ma/ρ)2。

D2cos2Vsin2A(mV/ρ)2+D2sin2Vcos2A(ma/ρ)2。

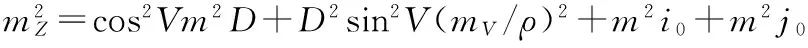
点位的平面误差为：

m2=sin2V(mD/D)2·D2+D2cos2V(mV/ρ)2+D2sin2V(ma/ρ)2。

因为放样时竖直角一般很小，即天顶距V接近于90°，则上式又可写成：

m2=(mD/D)2·D2+D2(ma/P)2

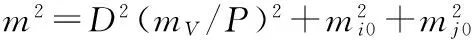
由此可知，当仪器的测角误差，测距误差和仪器高度、棱镜高度的误差确定后，放样点的精度决定于放样边长，对于测距中误差mD=3mm+2ppm，测角中误差ma=mV=±1.5，mi0=mj0=±1mm，则不同边长的放样精度如表3所示。

表3 放样精度表

5 结语

1)通过在平面控制测量中，将线路中线上的点纳入导线网坐标系统下，使整个线路每条曲线的坐标系不再相互独立，产生了联系。

2)以导线控制点作为置镜的任意点，提高了曲线测设的精度。

[1] 朱成粼,王兆祥.铁道工程测量学[M].北京：中国铁道出版社，2013.

[2] TB 10101— 99,新建铁路工程测量规范[S].

[3] 同济大学数学教研室.高等数学[M].北京：高等教育出版社，2007.

On curve design and measurement with polar coordinate method and its error analysis

Zhang Ruihua

(TaiyuanJinwantongRoadSurveyandDesignCo.,Ltd,Taiyuan030006,China)

According to the analysis of the controlled measurement results, the paper points out the curve intersection coordinate’s solution method under the same assumed coordinate, illustrates the application of the polar coordinate method in designing and measuring curves, and researches the sampling errors, so as to provide some reference.

polar coordinate method, curve, intersection coordinate, sampling error

1009-6825(2016)22-0192-02

2016-05-24

张瑞花(1979- )，女，助理工程师

TU198

A