Maxwell阻尼耗能多层结构在有界噪声激励下的随机响应解析分析
李创第,华逢忠,葛新广
(广西科技大学土木建筑工程学院,广西柳州545006)
Maxwell阻尼耗能多层结构在有界噪声激励下的随机响应解析分析
李创第,华逢忠,葛新广
(广西科技大学土木建筑工程学院,广西柳州545006)
为研究Maxwell阻尼器耗能多层结构在有界噪声激励下的随机响应问题,首先,建立了耗能结构时域非扩阶微分积分动力方程;然后,用传递函数法,获得了结构以第一振型表示的时域瞬态位移和速度响应非扩阶解析解;最后,基于此解析解,获得耗能结构在有界噪声激励下位移和速度随机响应方差解析解,并给出算例,从而建立此种耗能结构在有界噪声激励下随机响应解析分析的一整套方法.
Maxwell阻尼器;传递函数法;有界噪声激励;平稳响应;解析解
0 引言
粘弹性阻尼器耗能性能优良,已广泛应用于各种结构的被动减振控制[1-3].Maxwell阻尼[1-9]本构方程简单,模型计算参数易于从试验中拟合[10-11],且一般流体阻尼器比较符合Maxwell模型,粘弹性阻尼器也可以用Maxwell模型近似表示,故对Maxwell模型的应用研究受到日益重视[1-5,7-8].目前,分析Maxwell阻尼器耗能结构的精确法只有扩阶复模态法[4-5,7-8,12],但该法因扩阶方程组物理意义不明确,变量个数激增,计算效率低使该方法的实际应用受到限制.
有界噪声随机激励模型[13-15]不仅可以模拟宽带随机激励,而且可以模拟窄带随机激励;不仅可以模拟地震激励[16-17]、脉动风激励[18-20],而且还可以模拟轨道和路面随机起伏激励[21],因而受到国内外较广泛的应用[22-24].
本文采用非扩阶微分积分方程精确建模,运用传递函数法,获得Maxwell阻尼耗能多层结构在任意激励下非扩阶时域瞬态响应解析解和有界噪声激励下平稳随机响应解析解.
1 运动方程
设n层结构质量、刚度和粘滞阻尼矩阵分别为:M,K和C;层间质量、刚度和阻尼分别为:mi,ki和ci,(i=1,…,n);各层间均设置Maxwell阻尼器,阻尼器刚度系数和阻尼系数为k0i和c0i,阻尼力为pi(t),(i=1,…,n);x(t)为结构相对于地面的位移向量,F(t)为激励向量;结构计算简图如图1所示,由D’Alembert原理[25],结构的运动力程为:

式中:αi=k0i/c0i,i=1,…,n;
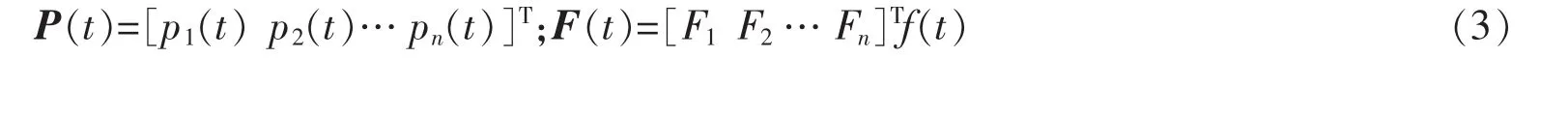


图1 多层耗能结构计算简图Fig.1 Calculation diagram of the multistorey energy dissipation structure
特别地,对地震激励,Fi=mi,(i=1,…,n);f(t)=-x¨g(t),x¨g(t)为地震地面加速度.
式(2)的分量形式为:
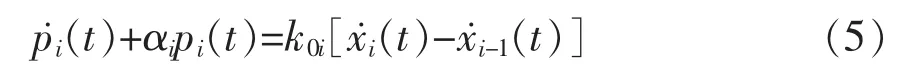
对于方程:

式中:δ(t)为Dirac delta函数.
方程(6)两边同时乘以eαit,即:
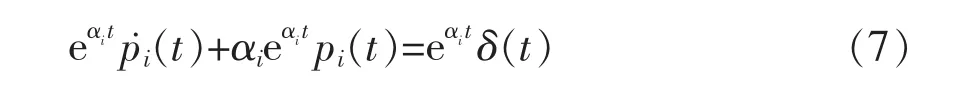
也即:

2 广义位移瞬态响应分析的传递函数法
2.1结构特征值分析
设结构的广义初始位移y(t=0)和速度y˙(t=0)均为0,对式(14)进行拉谱拉斯变换,得:

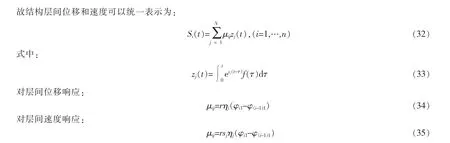
3 耗能结构平稳随机响应解析分析
3.1有界噪声激励的相关函数和谱密度
有界噪声激励f(t)的相关函数Cf(τ)和谱密度Sf(ω)分别为[16-20]:

式中:E[·]表示取数学期望;τ和ω分别为f(t)的时差和频率变量;D,α和β分别为激励的方差、相关因子和卓越频率因子.
特别地,对于地震激励x¨g(t),可取为[16-17,26]:
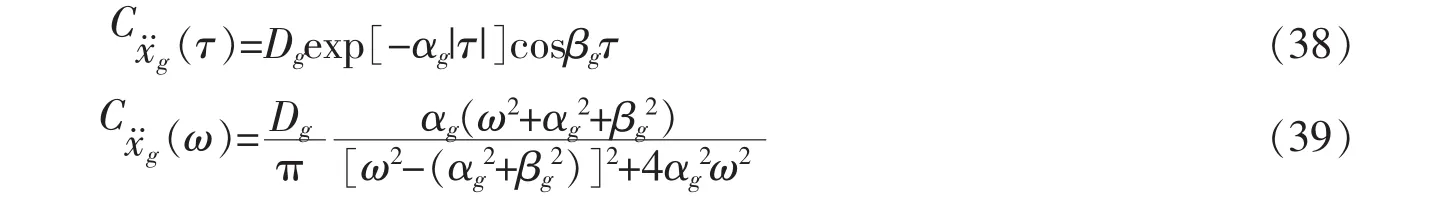
3.2耗能结构平稳随机响应解析分析
由式(32)得结构平稳响应方协方差为:
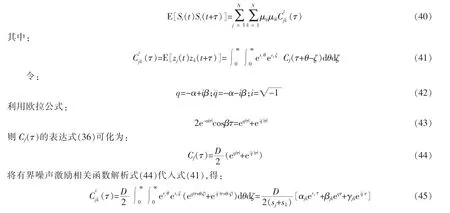
式中:

将式(45)代入式(40),并令τ=0,得有界噪声激励下耗能结构随机响应方差解析解:

特别地,对于地震激励,Fi=mi,f(t)=-x¨g;在表达式(45)中,令D=Dg;q=-αg+iβg;Fi=mi,式(49)即可表示为耗能结构随机地震响应方差解析解.
4 算例
软土场地条件下,3层框架结构各层的质量m1,m2和m3分别为:16 t,16 t和8 t;各层刚度k1,k2和k3分别为:1.0×105kN/m,1.0×105kN/m和1.0×105kN/m;取第一振型阻尼比ξ1=5%;结构第一振型φ1=[0.500,0.866,1.000]T,第一振型频率ω1为12.941 rad/s.Maxwell阻尼器参数如表1所示.8度抗震设防:I=8;ξg=0.96,ωg=10.9 rad/s.可以由式(20),解得结构各特征值sj;再利用式(22),得到系数ηj;最后各参数代入式(49),得到结构各层间位移和速度响应的方差.结构各层间位移和速度响应的标准差列于表2和表3.

表1 Maxwell阻尼器参数Tab.1 Calculation parameters of Maxwell dampers

表2 位移响应标准差Tab.2 Standard deviations of displacement responses m

表3 速度响应标准差Tab.3 Standard deviations of velocity responses m/s
表2和表3分别列出了表1中各工况对应的位移响应均方差和速度响应均方差.工况1是不设置Maxwell阻尼器的情况;工况2和工况3是同比例放大Maxwell阻尼器参数的情况,即工况2和工况3的Maxwell阻尼器具有相同的松弛时间;工况3与工况4的Maxwell阻尼器具有相同的阻尼系数但松弛时间不相同.计算结果表明:在松弛时间相同的情况下,Maxwell阻尼器参数越大,结构减震效果越明显;在阻尼系数相同的情况下,Maxwell阻尼器的松弛时间越小,结构减震效果越明显.
5 结论
对设置Maxwell阻尼器耗能多层结构在有界噪声激励下的平稳响应进行了研究.获得了结构以第一振型表示的时域瞬态位移和速度响应解析解,并根据所得的解析解,获得了耗能结构在有界噪声激励下位移和速度随机响应方差解析解,从而建立此种耗能结构在有界噪声激励下随机响应解析分析的一整套方法.由于有界噪声激励模型可以模拟多种工程随机激励,故所获得的解析解具有较好的工程应用意义.
[1]周云.粘弹性阻尼减震结构设计[M].武汉:武汉理工大学出版社,2006.
[2]SOONGTT,DARGUSH GF.Passive Engrgy Dissipation Systems in Structural Engineering[M].England:John Wiley and Ltd,1997.
[3]CHRISTOPOULOS C,FILIATRAULT A.Principle of Passive Supplemental Damping and Seismic Isolation[M].Pavia:IUSS Press,2006.
[4]YAMADA K.Dynamic Characteristics of SDOF Structure with Maxwell Element[J].Journal of Engineering Mechanics,2014,134(5):396-404.
[5]PALMERI A,RICCIARDELLI F,DELUCA A,et al.State Space Formulation for Linear Viscoelastic Dynamic Systems with Memory[J].Journal of Engineering Mechanics,2003,129(7):715-724.
[6]张义同.粘弹性理论[M].天津:天津大学出版社,2002.
[7]PALMERI A.Correlation Coefficients for Structures with Viscoelastic Dampers[J].Engineering Structures,2006,28(8):1197-1208.
[8]SINGH M P,VERMA N P,MORESCHIL M.Seismic Analysis and Design with Maxwell Dampers[J].Journal of Engineering Mechanics,2003,129(3):273–282.
[9]葛新广,李创第,邹万杰.Maxwell阻尼减震结构的最大非平稳响应[J].广西工学院学报,2012,23(4):1-7.
[10]CHANG T S,SINGH M P.Mechanical Model Parameters for Viscoelastic Dampers[J].Journal of Engineering Mechanics,2009,135(6):581-584.
[11]PARK SW.Analytical Modeling of Viscoelastic Dampers for Structural and Vibration Control[J].International Journal of Solids and Structures,2001,38(S44-45):8065-8092.
[12]ZHANG R H,SOONG T T.Seismic Design of Viscoelastic Dampers for Structural Application[J].Journal of Structural Engineering,1992,118(5):1375-1392.
[13]HUANG Z L,ZHU W Q,NI Y Q,et al.Stochastic Averaging of Strongly Non-Linear Oscillators under Bounded Noise Excitation[ J].Journal of Sound and Vibration,2002,254(2):245-267.
[14]LIU W Y,ZHU W Q,HUANG Z L.Effect of Bounded Noise on Chaotic Motion of Duffing Oscillator under Parametric Excitation[J].Chaos,Solitons and Fractals,2001,12(3):527–537.
[15]ZHU W Q,HUANG Z L,YANG Y Q.Stochastic Averaging of Quasi-Integrable Hamiltonian Systems[J].Journal of Applied Mechanics,1997,64(4):975–984.
[16]胡聿贤.地震工程学[M].2版.北京:地震出版社,2006.
[17]李桂青.抗震结构计算理论和方法[M].北京:地震出版社,1985.
[18]LIN Y K,LIQ C.Stochastic Stability of Wind Excited Structures[J].Journal of Wind Engineering and Industrial Aerodynamics,1995,54(94):75-82.
[19]LIN Y K.Stochastic Stability of Wind-Excited Long-S pan Bridges[J].Probabilistic Engineering Mechanics,1996,11(4):257-261.
[20]LIN Y K,LI Q C.New Stochastic Theory for Bridge Stability in Turbulent Flow[J].Journal of Engineering Mechanics,1993,119(1):113–127.
[21]DIMENTBERG M F.Stability and Subcritical Dynamics of Structures with Spatially Disordered Travelling Parametric Excitation[J]. Probabilistic Engineering Mechanics,1992,7(3):131–134.
[22]刘雯彦,陈忠汉,朱位秋.有界噪声激励下单摆—谐振子系统的混沌运动[J].力学学报,2003,35(5):634-639.
[23]XIE W C.Moment Lyapunov Exponents of a Two-Dimensional System under Bounded Noise Parametric Excitation[J].Journal of Sound and Vibration,2003,263(3):593-616.
[24]ZHU J,XIE W C,SO R M,et al.Parametric Resonance of Two Degrees of Freedom System Induced by Bounded Noise[J].Journal of Applied Mechanics,2009,76(4):041007-1~13.
[25]刘晶波,杜修力.结构动力学[M].北京:机械工业出版社,2005.
[26]李桂青,曹宏,李秋胜,等.结构动力可靠性理论及其应用[M].北京:地震出版社,1993.
(学科编辑:黎娅)
Exact analysis of the random responses of multi-storey structure with Maxwell dampers under bounded noise excitation
LI Chuang-di,HU A Feng-zhong,GE Xin-guang
(School of Civil Engineering and Architecture,Guangxi University of Science and Technology,Liuzhou 545006,China)
The random responses of multi-storey structure with Maxwell dampers under bounded noise excitation are studied.Firstly,the structural non-extended order differential-integral dynamic response equations are established;Then,by using transfer function method,the exact solutions of structural transient displacement and velocity responses in time-domain are obtained by expanding the structure with respect to the first mode.Finally,by using above exact solutions,analytical solutions of the response variances of the displacement and velocity of energy dissipation structure under the bounded noise excitation are obtained.Therefore,a complete set of analytical method for the stochastic response of the energy dissipation structure under bounded noise excitation is established and a numerical example is given.
Maxwell dampers;transfer function method;bounded noise excitation;stationary response;exact solutions
TU311.3
A
2095-7335(2016)04-0001-06
10.16375/j.cnki.cn45-1395/t.2016.04.001
2016-03-30
国家自然科学基金项目(51468005,51368008);广西自然科学基金项目(2014GXNSFAA118315);广西科技大学创新团队支持计划项目(2015年)资助.
李创第,博士,教授,研究方向:被动控制结构抗风抗震,E-mail:lichuangdi1964@163.com.

