基于微课学习·历经认知过程·领略思想方法——以“圆的知识”学习微课设计为例

□浙江省杭州市景芳中学 吴洁慧

□浙江省杭州市江干区教育发展研究院 易良斌

基于微课学习·历经认知过程·领略思想方法
——以“圆的知识”学习微课设计为例

□浙江省杭州市景芳中学 吴洁慧

□浙江省杭州市江干区教育发展研究院 易良斌

微课又名微型课程，是指以微型教学视频为主要载体，教师针对某个学科知识点、技能点或教学环节而设计开发的一种情景化、支持多种学习方式的在线视频网络课程。“微课程”一般在10分钟以内，以使学习者自主学习获得最佳效果。微课的特质决定它“简约而不简单，聚焦而不宽泛”。基于这样的思考，一个有价值的微课首先要关注“学什么”，从数学学习的角度来说，即数学学习的核心价值所在，就是数学知识的核心原动力——数学思想方法。

一、忽视弦与圆心的位置关系造成漏解问题

1.微课背景。圆是重要的几何图形之一。由于图形位置、形状、大小不确定，决定了网中某些问题为多解问题，在解答时极易产生漏解。因此，解答这类问题时一定要仔细分析，缜密思考，充分运用分类讨论思想，正确画图，逐一解答，才能圆满解题，切忌因思维定势或考虑不周而造成漏解。

2.微课目标。

（1）经历探索解决有关弦和圆心的不同位置关系产生不同解的过程，积累数学活动经验；

（2）理解并领悟分类讨论思想在解题中的重要性，并能提炼出分类思想的精髓就是找到分类的依据，也就是明确分类标准。

3.微课设计。

（1）一圆两弦。

问题1：这道关于圆的几何题，没有图，不方便，你能把图画出来吗？

问题2：和小组内的同学互相看看，比较一下，你们画的图一样吗？讨论一下这是为什么？你分类的标准是什么？

问题3：画好图了，为了求解我们是否需要画辅助线？你添线的目的是什么？

问题4：过程中，你用到了哪些知识点？

【解法指导】

解法一：如图1，当点D、C在AB的异侧时，连结CO、DO。

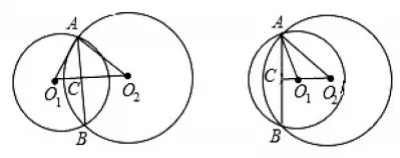
例2.已知两圆的半径分别为10cm、17cm，公共弦长为16 cm，求圆心距的长。

问题1：这道同样关于圆的几何题，没有图，不方便，你能把图画出来吗？

问题2：和小组内的同学互相看看，比较一下，你们画的图一样吗？讨论一下这是为什么？这次你分类的标准又是什么？

问题3：画好图了，为了求解我们是否需要画辅助线？你添线的目的是什么？

问题4：过程中你用到了哪些知识点来帮助我们计算？

【解法指导】

考点：圆与圆的位置关系，弦径定理，勾股定理。

分析：设⊙O1的半径为r=10，⊙2的半径为R=17，公共弦为AB，两圆的圆心的连线与公共弦的交点为C；那么根据垂径定理，AC=BC=8，且出现两个直角三角形：△O1AC和△O2AC。利用勾股定理可求出O1C和O2C，就可求出O1O2：

在Rt△O1AC中，

同理，在Rt△O2AC中，O2C=6。

∴O1O2=O1C+O2C=15+6=21（cm）左图，

或O1O2=O2C-O1C=15-6=9（cm）右图。

练习：

1.⊙O的半径为10cm，两平行弦AC，BD的长分别为12cm，16cm，则两弦间的距离是（）

A.2cmB.14cmC.6cm或8cmD.2cm或14cm

（3）小结。本节微课中由于没有图，因此弦与圆心的位置就会有不同的可能性，分类讨论就是要抓住分类的标准，在这里，两弦一圆，就是关注圆心是在两弦的同侧还是异侧；两圆一弦，就要关注这条公共弦是在两圆心的同侧还是异侧。

除了分类讨论思想的渗透，本节课还综合了有关三角函数，勾股定理等知识点，对于知识的综合运用能力较强，我们一定要在解题过程中明确推理的条件和结论，用好用对每一个知识点。

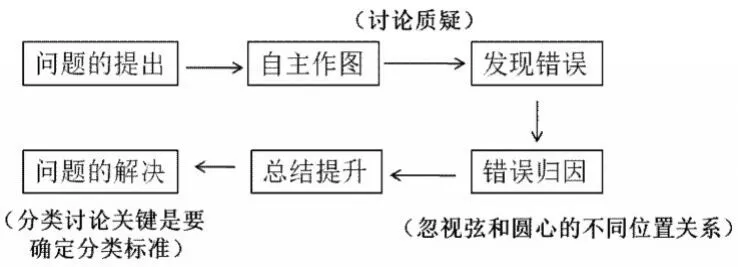
4.设计说明。本节课的设计思路：

二、在圆的背景下的相似问题

1.微课背景。推理能力是《义务教育数学课程标准》提出的十大数学课程核心概念之一。发展学生的推理能力历来是数学课程的一个重要功能，几何教学对学生推理能力的发展作用是不言而喻的。如何在几何教学中发展学生的推理能力，是几何教学的重中之重。

“分析法”是演绎推理的一个重要的方法，一个学生分析问题能力的高低，往往决定着这个学生解决问题能力的强弱。本节微课采用“箭头式”的反推分析，对提高学生的推理能力非常有利，条理也非常清晰。

2.微课目标。

（1）会用“分析法”进行演绎推理，培养学生推理能力。

（2）会灵活运用圆和相似的相关知识，提高解决问题的综合能力。

（3）渗透从“未知”到“已知”的转化思想。

3.微课设计。

（1）试题呈现。

例3.（2015天水）如图，AB是⊙O的直径，BC切⊙O于点B，OC平行于弦AD，过点D作DE⊥AB于点E，连结AC，与DE交于点P.求证：

（1）AC·PD=AP·BC；

（2）PE=PD。

（2）解法探究。

分析：（1）首先根据AB是⊙O的直径，BC是切线，可得AB⊥BC，再根据DE⊥AB，判断出DE∥BC，△AEP∽△ABC，所以=；然后判断出=，即可判断出ED=2EP，据此判断出PE=PD。

（2）首先根据△AEP∽△ABC，判断出；然后根据PE=PD，可得，据此判断出AC·PD=AP·BC即可。

用“箭头式”的分析图可以更加清晰：

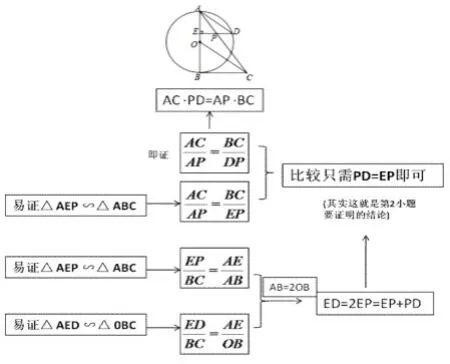
【解答示例】解：先证第二小题。

点评：（1）此题主要考查了切线的性质和应用，要熟练掌握，解答此题的关键是要明确：①圆的切线垂直于经过切点的半径.②经过圆心且垂直于切线的直线必经过切点.③经过切点且垂直于切线的直线必经过圆心.

（2）此题还考查了相似三角形的判定和性质的应用，要熟练掌握.

（3）巩固练习。（略）

（4）小结。

（5）设计说明。这节微课用时10分钟左右，运用“综合分析法”来解答的方法教学，即是“由果索因”，使学生对这种解题策略有深刻的认识和理解，并进行深入思考，实现条件和结论的转化，从而深刻领会数学核心思想中的转化的思想。