航天器自适应快速非奇异终端滑模容错控制
韩治国, 张科,*, 吕梅柏, 郭小红
1.西北工业大学 航天飞行动力学技术重点实验室, 西安 710072 2.西北工业大学 航天学院, 西安 710072 3.西安卫星测控中心, 西安 710043
航天器自适应快速非奇异终端滑模容错控制
韩治国1,2, 张科1,2,*, 吕梅柏1,2, 郭小红3
1.西北工业大学 航天飞行动力学技术重点实验室, 西安 710072 2.西北工业大学 航天学院, 西安 710072 3.西安卫星测控中心, 西安 710043
针对存在外部干扰、转动惯量矩阵不确定、控制器饱和以及执行器故障的航天器姿态跟踪控制问题,提出了基于自适应快速非奇异终端滑模的有限时间收敛控制方案。通过引入能够避免奇异点的具有有限时间收敛特性的快速非奇异终端滑模面,设计了满足多约束的有限时间姿态跟踪容错控制器,并利用参数自适应方法使控制器设计不依赖于系统惯量信息和外部干扰的上界。此外,所设计的控制器显式考虑了执行器输出力矩的饱和幅值特性,使航天器在饱和幅值的限制下完成姿态跟踪控制任务,并且无须进行在线故障估计。Lyapunov稳定性分析表明:在外部干扰、转动惯量矩阵不确定、控制器饱和以及执行器故障等约束条件下,所设计的控制器能够保证闭环系统的快速收敛性,而且对控制器饱和与执行器故障具有良好的容错性能。数值仿真校验了该控制器在姿态跟踪控制中的优良性能。
航天器; 姿态跟踪; 执行器故障; 有限时间; 控制器饱和
航天器姿态控制系统在航天器的健康运行中扮演着重要的角色。在复杂的航天环境中,航天器姿态控制系统会受到各种外部干扰力矩的作用,航天器执行器在长期不断地执行在轨控制操作时也会存在老化和失效等故障。为了有效维持控制系统性能,需要使其对外部干扰与执行器故障具有较强的鲁棒性;另外,航天器还存在转动惯量矩阵的不确定性,因此控制饱和也是航天工程中的常见问题[1-2]。综上所述,航天器在执行跟踪任务时,需要一种能在有限时间内使系统收敛的高稳定度、高精度的容错控制方法[3-4]。
对于非线性系统,滑模控制是一种有效的容错控制方法,并且对于系统不确定项具有较强的鲁棒性。目前,应用滑模控制进行刚体航天器控制系统设计已经取得了许多研究成果[5-10]。在容错控制方面:文献[5-7]研究了外部干扰作用下的滑模姿态跟踪控制;文献[8-9]研究了执行器故障下的有限时间姿态容错控制;文献[10-11]研究了执行器故障下的自适应补偿控制。
上述研究中所设计的控制系统并没有考虑控制器的饱和特性,只是在仿真中对控制量的上限进行了约束;但在实际工程中,控制器饱和是经常发生的,因此研究控制器饱和特性下的有限时间控制具有较强的工程意义。文献[12-15]研究了执行器饱和特性下的基于滑模的有限时间姿态跟踪控制;文献[16]研究了基于反步法的有限时间姿态跟踪控制;文献[17-20]研究了基于非奇异滑模面的航天器有限时间姿态跟踪控制,同时文献[19]利用参数自适应方法对滑模面的趋近律参数进行了估计。
综合上述研究成果,虽然部分文献在考虑控制器饱和特性下设计了有限时间收敛的故障容错控制律,但是设计的控制律仍然依赖于系统不确定性的上界。因此在综合考虑控制器饱和与执行器故障等控制问题时,如何实现在存在外部干扰与惯量矩阵不确定下的有限时间收敛控制,提高控制精度与减小控制器抖动,并利用参数自适应方法使设计的控制律不依赖系统不确定性的上界信息,成为本文的研究重点。本文首先引入快速非奇异终端滑模面,然后基于参数自适应设计了有限时间姿态跟踪容错控制器,并根据Lyapunov稳定性理论进行了稳定性证明,最后根据仿真实例验证上述方法的可行性。
1 姿态跟踪数学模型
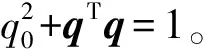
(1)
式中:w=[w1w2w3]T∈R3为航天器本体系Fb相对于惯性坐标系Fi的角速度在Fb上的投影;u=[u1u2u3]T∈R3为实际作用于航天器本体系坐标轴上的总控制力矩;d=[d1d2d3]T∈R3为航天器受到的外部干扰力矩;矩阵J∈R3×3(正定且对称)为航天器转动惯量;D∈R3×N为反作用飞轮控制力矩分配矩阵且行满秩,N为反作用飞轮的个数。对于向量a=[a1a2a3]T,矩阵a×∈R3×3为
(2)
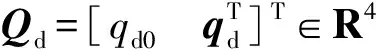
(3)
we=w-Cwd
(4)
则根据方程式(1)、(3)与(4)可得开环航天器姿态跟踪数学模型为[16]
(5)
(6)
在进行控制器设计之前,首先给出如下合理假设。
假设1卫星的姿态角q和姿态角速率w可测,可以基于姿态角q和姿态角速率w设计反馈控制律。
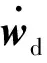
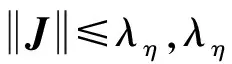
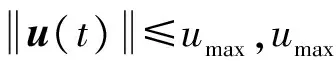
对于上述假设,文献[5,8,12,14]中均有表述,并且给出了合理说明,本文在此不再赘述。
根据参考文献[13],执行器故障可以写为
(7)
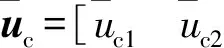
根据假设3与执行器故障形式(7),姿态跟踪误差方差式(6)可以进一步写为
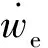
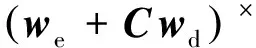
(8)
考虑执行器的输出饱和特性:
us=sat(uc)
(9)
式中:uc为待设计的控制器。把式(9)代入式(8),可得
(10)
式中:
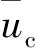
(11)
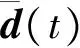
饱和非线性项sat(uc)代表执行器的饱和非线性特性,具有下列形式[5]:
(12)
式中:i=1,2,…,N。为简单起见,非线性项sat(uc)能够写为
sat(uc(t))=Θ(uc(t))uc(t)
(13)
式中:Θ(uc(t))=diag(Θ1(uc1(t)),Θ2(uc2(t)),…,ΘN(ucN(t)))并且
(14)
式中:Θi(uci(t))为执行器饱和程度的指示器。Θi(uci(t))越小,执行器的饱和程度越大。根据文献[5],有
0<δ≤min(Θi(uci(t)))≤1
(15)
式中:δ为大于零的未知常量。
2 故障容错控制器设计
在进行容错控制器设计之前,首先定义控制目标,接下来应用快速非奇异终端滑模控制方法设计控制律,最后给出稳定性证明。为了补偿执行器饱和、执行器故障、外部干扰与转动惯量矩阵不确定带来的影响,设计具有参数自适应的有限时间趋近律。该设计方法基于以下3步完成。
1) 滑模面设计。
2) 具有参数自适应的控制律设计。
3) 到达阶段与稳定阶段的稳定性证明。
2.1 控制目标
在存在外部干扰、转动惯量矩阵不确定、执行器饱和与执行器故障的情况下,设计一个鲁棒容错控制器确保系统在有限时间内稳定是本文的控制目标。即:在有限时间内,误差四元数Qe趋于[1 0 0 0],角速度误差we趋于零。上述控制目标可描述为
(16)
2.2 控制器设计
为了与现有的容错控制方法进行对比,本文选择能够避免奇异点与具有快速收敛的非奇异终端滑模面,因此,根据角速度误差与误差四元数,选择如下的滑模面[19]:
Se=sigα(we)+βsigα(qev)+λqev
(17)
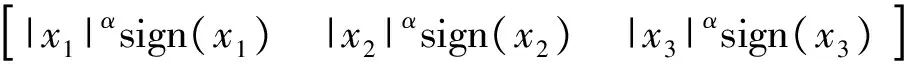
(18)
式中:i=1,2,3。把式(10)代入式(18),可得
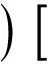

(19)
趋近律设计为
(20)
式中:ki=diag(ki1,ki2,ki3)(i=1,2)为对角矩阵,kij>0(j=1,2,3)为待定参数;γ∈(0,1)。
假设6存在未知常数c1≥0以及c2≥0使得式(20)和式(21)成立:
(21)
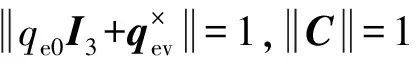
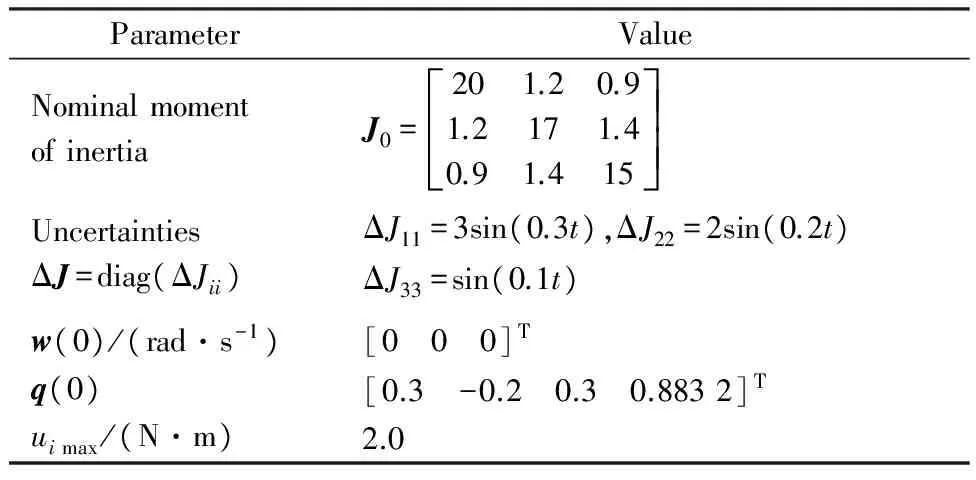
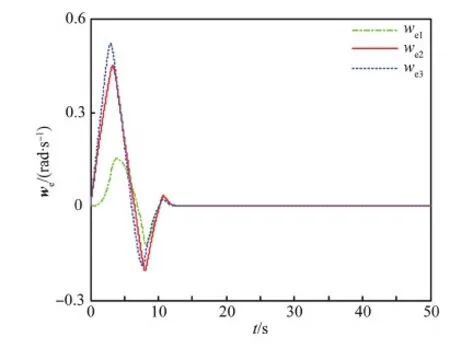
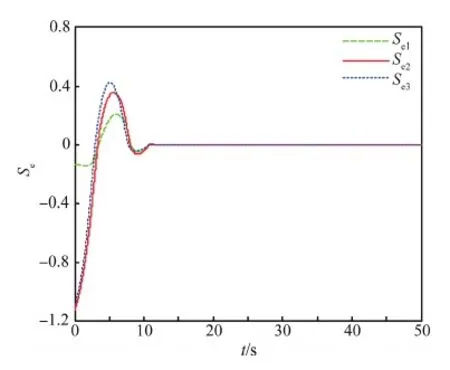
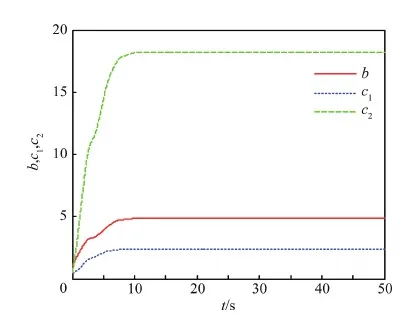
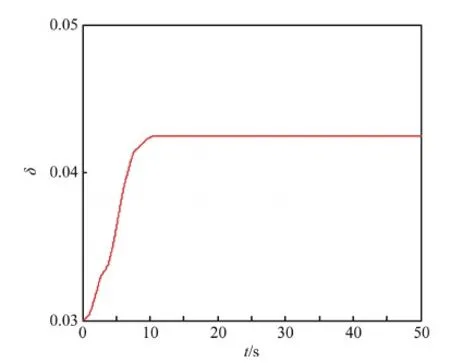
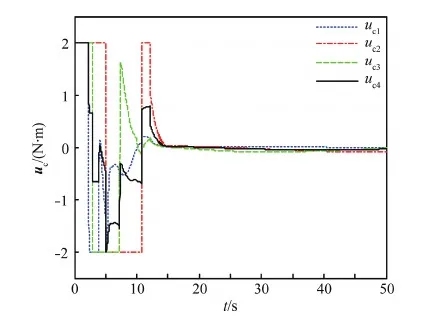
引理1对于任意给定的实数λ1>0,λ2>0,0 (22) 则系统状态能够在有限时间内到达原点,时间为 (23) 定理1考虑存在执行器饱和、执行器故障、转动惯量矩阵不确定以及外部干扰的航天器系统式(5)和式(10),以及设计的滑模面式(17),在满足假设1~6的条件下,应用式(24)定义的控制方案,则闭环系统的轨迹将在有限时间内趋近到滑模面。 uc(t)=D÷-k1Se-k2sigγ(Se)- (24) (25) (26) (27) (28) 证明选取如下的Lyapunov函数: (29) (30) 根据假设6,可得 (31) 把控制律式(24)及自适应律式(25)~式(28)代入式(31),可得 (32) (33) 因此,当we≠0时,根据引理1可得,系统在有限时间内趋近到滑模面,且收敛时间为 (34) 当we=0时,把设计的控制律代入式(10)可得 (35) 定理2对于给定的系统式(5)和式(10),当系统状态到达滑模面Se=0的邻域时,跟踪误差将在有限时间内收敛到零点[19]。 证明系统状态到达滑模面时,可以得到 Se=sigα(we)+βsigα(qev)+λqev=0 (36) 因此 we≤-β1/αqev-λ1/αsig1/α(qev) (37) 定义如下的Lyapunov函数: (38) 则有 (39) 40 (41) 因此,根据引理1,当系统轨迹到达滑模面以后,则四元数误差将在有限时间内趋于零。令t2为到达滑模面的时间,则有 (42) 因此,根据定理2,四元数误差将在有限时间内趋于零,则根据误差方程式(5)可得,角速度误差将在有限时间内趋于零,即:we→0。证毕。 注1根据式(34)可知,参数α,k1,k2对系统的收敛速度有影响,根据式(42)可知,参数β和λ对系统的收敛速度也有影响。上述参数取较大的值将加快系统的收敛速度。然而,较大的参数使系统的控制量也将增大,因此在选择参数α,k1,k2,β和λ时,应该综合考虑系统的收敛速度与控制输入的幅值要求。 注2根据控制律式(24)可知,本文设计的控制律不依赖于转动惯量J,因此本文设计的控制律可以应用于具有转动惯量矩阵不确定的姿态控制系统。 注3根据式(32)可知,参数δ,η对系统的收敛速度与控制精度具有重要的影响,参数δ根据自适应律进行估计,参数η的选取需要满足系统要求。 注4本文根据文献[19]设计的滑模面设计了参数自适应控制器,相比文献[19],本文设计的控制器不依赖转动惯量与系统外部干扰的上界信息,通过设计自适应参数与控制器参数,系统滑模面能够到达平衡点任意小的邻域内,而文献[19]的收敛域依赖外部不确定性的上界。 另外,为了减小系统抖动,采用式(43)所示的控制形式代替式(24)。 (43) 式中:ε为很小的正常数。 仿真实验中,考虑的外部干扰为 (44) 期望姿态角初值及期望角速度初值分别为 (45) 航天器的主要参数设置如表1所示。仿真过程中使用的控制器参数如表2所示。 表1 航天器主要参数Table 1 Main parameters of spacecraft 表2 控制器参数Table 2 Parameters of controller 仿真中,考虑执行器故障形式为 (46) (47) 式中:i=1,2,3,4。 控制力矩分配矩阵为 (48) 根据上述仿真参数设置,得到的仿真结果如图1~图6所示。图1和图2分别为航天器本体系相对于期望坐标系的相对姿态四元数误差及角速度误差响应曲线。从图1和图2中可以看出,本文所设计的控制器能以较快的速度及较高的控制精度达到姿态跟踪的目的,跟踪收敛时间仅为10.67 s,误差四元数的稳态值达到8.1×10-5,角速度误差稳态值达到5.8×10-5。 图3为控制力矩响应曲线。从图中可以看出,本文设计的控制器的控制力矩满足最大幅值限制要求,控制器抖动小。图4为滑模面变化曲线。图5和图6为自适应参数变化曲线。综上所述,本文设计的控制器应用于航天器姿态跟踪控制具有良好的控制能力和较快的收敛速度。 为了充分证明本文设计的控制器的有效性,考虑式(49)表示的执行器故障: 图1 四元数误差响应曲线Fig.1 Response curves of quaternion errors 图2 角速度误差响应曲线Fig.2 Response curves of angular velocity errors 图3 控制力矩响应曲线Fig.3 Response curves of control torques 图4 滑模面响应曲线Fig.4 Response curves of sliding mode 图5 自适应参数响应曲线Fig.5 Response curves of adaptive parameter 图6 控制器饱和响应曲线Fig.6 Response curves of controller saturation (49) 式中:i=1,2,3,4。 表3为采用本文设计的控制律式(24),在故障式(46)与式(49)情形下的控制性能对比。从表中可以看出,在增加执行器效率下降矩阵后,系统仍具有很好的性能,只是在故障式(49)情形下系统收敛时间相对故障式(46)略有增加。 为了进一步说明本文方法的优越性,与文献[19]设计的自适应控制律进行对比仿真。图7为采用文献[19]设计的自适应控制律得到的控制力矩响应曲线。通过与图3对比可以看出,采用文献[19]的设计方法得到的控制力矩曲线波动大,系统收敛时间长。同时,根据表3可以看出,控制量在最大幅值约束条件下,文献[19]设计的控制律的收敛时间明显大于本文设计方法的收敛时间。另外,文献[19]的误差四元数的稳态值为1.3×10-3,角速度误差稳态值为7.2×10-3,系统的稳态误差也大于本文设计方法的稳态误差。 表3 控制性能对比Table 3 Comparison of control performance 图7 文献[19]的控制力矩响应曲线Fig.7 Response curves of control torques in Ref.[19] 本文的自适应有限时间收敛故障容错控制律设计方法具有如下优势: 1) 该控制方案具有较好的执行器故障容错能力与控制器饱和控制能力,以及对外部干扰与转动惯量的不确定性具有较好的鲁棒性。 2) 本文设计的控制方案实现了有限时间姿态跟踪控制,具有较快的收敛速度和较高的精确控制性能。 [1] HU Q L, LI B, ZHANG A H. Robust finite-time control allocation in spacecraft attitude stabilization under actuator misalignment[J]. Nonlinear Dynamics, 2013, 73(1): 53-71. [2] PUKDEBOON C, ZINOBER S I A, THEIN M W L. Quasi-continuous higher order sliding-mode controllers for spacecraft-attitude-tracking maneuvers[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1436-1444. [3] YEH F K. Sliding-mode adaptive attitude controller design for spacecraft with thrusters[J]. IET Control Theory and Applications, 2010, 4(7): 1254-1264. [4] JIN J, KO S, RYOO C K. Fault tolerant control for satellites with four reaction wheels[J]. Control Engineering Practice, 2008, 16(10): 1250-1258. [5] LU K F, XIA Y Q, ZHU Z, et al. Sliding mode attitude tracking of rigid spacecraft with disturbance[J]. Journal of the Franklin Institute, 2012, 349(2): 413-440. [6] XIA Y Q, ZHU Z, FU M Y, et al. Attitude tracking of rigid spacecraft with bounded disturbances[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 647-659. [7] ZHU Z, XIA Y Q, FU M Y. Attitude stabilization of rigid spacecraft with finite-time convergence[J]. International Journal of Robust and Nonlinear Control, 2011, 21(6): 686-702. [8] HU Q L, HUO X, XIAO B, et al. Robust finite-time control for spacecraft attitude stabilization under actuator fault[J]. Systems and Control Engineering, 2011, 10(1): 1-13. [9] CAO L, LI X L, CHEN X Q, et al. Minimum sliding mode error feedback control for fault tolerant small satellite attitude control[J]. Advances in Space Research, 2014, 53(2): 309-324. [10] CAO L, CHEN X Q, SHENG T. Fault tolerant small satellite attitude control using adaptive non-singular terminal sliding mode[J]. Advances in Space Research, 2013, 51(12): 2374-2393. [11] MA Y J, JIANG B, TAO G, et al. Actuator failure compensation and attitude control for rigid satellite by adaptive control using quaternion feedback[J]. Journal of the Franklin Institute, 2014, 351(1): 296-314. [12] 胡庆雷, 王辉, 石忠, 等. 航天器新型非奇异饱和终端滑模姿态控制[J]. 宇航学报, 2015, 36(4): 430-437. HU Q L, WANG H, SHI Z, et al. Novel non-singular saturated terminal sliding mode based attitude controller for spacecraft[J]. Journal of Astronautics, 2015, 36(4): 430-437 (in Chinese). [13] XIAO B, HU Q L. Fault-tolerant tracking control of spacecraft with attitude-only measurement under actuator failures[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(3): 838-849. [14] HU Q L, JIANG B Y. Robust saturated finite time output feedback attitude stabilization for rigid spacecraft[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(6): 1914-1929. [15] LU K F, XIA Y Q, FU M Y. Controller design for rigid spacecraft attitude tracking with actuator saturation[J]. Information Sciences, 2013, 220: 343-366. [16] 王辉, 胡庆雷, 石忠, 等. 基于反步法的航天器有限时间姿态跟踪容错控制[J]. 航空学报, 2015, 36(6): 1933-1939. WANG H, HU Q L, SHI Z, et al. Back stepping-based finite-time fault-tolerant attitude tracking control for spacecraft[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1933-1939 (in Chinese). [17] SHEN Q, WANG D W. Integral-type sliding mode fault-tolerant control for attitude stabilization of spacecraft[J]. IEEE Transactions on Control Systems Technology, 2015, 23(3): 1131-1138. [18] LU K F, XIA Y Q. Finite-time attitude stabilization for rigid spacecraft[J]. International Journal of Robust and Nonlinear Control, 2013, 25(1): 32-51. [19] TIWARI M P, JANARD S, NABI U M. Rigid spacecraft fault-tolerant control using adaptive fast terminal sliding mode[J]. Advances and Applications in Sliding Mode Control Systems, 2015, 12(3): 381-406. [20] HU Q L, HUO X, XIAO B. Reaction wheel fault tolerant control for spacecraft attitude stabilization with finite-time convergence[J]. International Journal of Robust and Nonlinear Control, 2012, 23(8): 1737-1752. 韩治国男, 博士研究生。主要研究方向: 航天器故障诊断与容错控制。 Tel.: 029-88492781 E-mail: xiaozuanfen888@163.com 张科男, 博士, 教授。主要研究方向: 飞行器制导与控制技术。 Tel.: 029-88494418 E-mail: zhangke@nwpu.edu.cn URL:www.cnki.net/kcms/detail/11.1929.V.20160106.1541.008.html Spacecraftfault-tolerantcontrolusingadaptivenon-singularfastterminalslidingmode HANZhiguo1,2,ZHANGKe1,2,*,LYUMeibo1,2,GUOXiaohong3 1.NationalKeyLaboratoryofAerospaceFlightDynamics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.SchoolofAstronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China3.ChinaXi’anSatelliteControlCenter,Xi’an710043,China Finite-timeconvergencecontrolstrategiesbasedonadaptivenon-singularfastterminalslidingmodeareproposedforspacecraftattitudetrackingsubjecttoexternaldisturbances,inertiauncertainties,controlsaturationandactuatorfaults.Afinite-timefault-tolerantattitudetrackingcontrollermeetingthemulti-constraintsisdevelopedbyintroducinganon-singularfastterminalslidingmodewithfinite-timeconvergenceandsingularitiesavoidanceattributes.Itisfurthershownthatthecontrollerisindependentfrominertiauncertaintiesandboundofexternaldisturbanceswithparameteradaptations.Inaddition,thecontrollerdesignedinthispaperexplicitlyconsiderstheactuatoroutputtorquesaturationamplituderequirements,whichmakesthespacecraftcompletethegivenoperationswithinthesaturationmagnitudeandwithouttheneedforon-linefaultestimate.TheLyapunovstabilityanalysisshowsthatthedesignedcontrollercanguaranteethefastconvergenceoftheclosed-loopsystemandhasagoodfaulttolerantperformanceoncontrolsaturationandactuatorfaultsunderthemulti-constraintsonexternaldisturbances,inertiauncertainties,controlsaturationandactuatorfaults.Numericalsimulationhasverifiedthegoodperformanceofthecontrollerintheattitudetrackingcontrol. spacecraft;attitudetracking;actuatorfaults;finite-time;controllersaturation 2015-10-19;Revised2015-11-24;Accepted2015-12-28;Publishedonline2016-01-061541 s:NationalNaturalScienceFoundationofChina(61101191,61174204,61502391);ChinaSpaceFoundation(N2015KC0121) .Tel.:029-88494418E-mailzhangke@nwpu.edu.cn 2015-10-19;退修日期2015-11-24;录用日期2015-12-28; < class="emphasis_bold">网络出版时间 时间:2016-01-061541 www.cnki.net/kcms/detail/11.1929.V.20160106.1541.008.html 国家自然科学基金 (61101191,61174204,61502391); 航天支撑基金 (N2015KC0121) .Tel.:029-88494418E-mailzhangke@nwpu.edu.cn 韩治国, 张科, 吕梅柏, 等. 航天器自适应快速非奇异终端滑模容错控制J. 航空学报,2016,37(10):3092-3100.HANZG,ZHANGK,LYUMB,etal.Spacecraftfault-tolerantcontrolusingadaptivenon-singularfastterminalslidingmodeJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3092-3100. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2015.0357 V448.2 A 1000-6893(2016)10-3092-09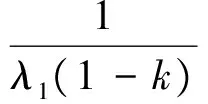
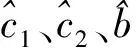
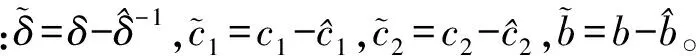




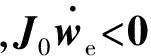
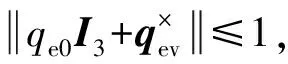


3 仿真结果与分析



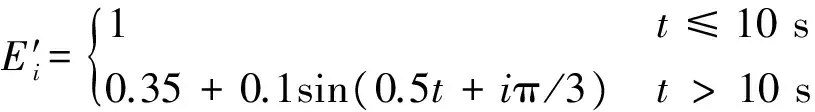

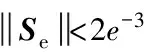
4 结 论

