充气机翼的褶皱与失效行为研究
李斌, 董楠楠, 冯志壮, 牛文超
西北工业大学 航空学院, 西安 710072
充气机翼的褶皱与失效行为研究
李斌*, 董楠楠, 冯志壮, 牛文超
西北工业大学 航空学院, 西安 710072
在经典工程梁理论的基础上,结合张力薄膜的应力状态分析,提出充气机翼褶皱失稳的判据。计入表面薄膜褶皱引起的刚度退化效应,将机翼等效处理为一个变截面刚度的梁,建立了充气悬臂机翼的等效梁模型,并采用微分求积法进行充气机翼弯曲变形分析。计算结果与充气机翼的静力弯曲试验结果相吻合,验证了充气机翼弯曲变形分析方法的有效性。应用片条理论引入气动力模型,并与所建立的等效梁模型相耦合,建立充气机翼的静气动弹性耦合模型,并用迭代算法进行求解。考虑起皱和失稳两种判据,并计算获取了试验机翼的起皱动压和皱褶失稳动压形式,计算结果与风洞试验结果一致。根据所建立的充气机翼静气动弹性分析方法,可以预测充气机翼表面褶皱区的扩展和弯曲变形,进而绘制充气机翼的静气弹许用包线,为充气机翼的设计提供必要的安全边界参考依据。
充气机翼; 褶皱; 变刚度; 静气弹; 失稳
薄膜充气结构具有质量轻、折叠体积小、展开迅速、可反复使用以及成本低等特点。近些年关于充气机翼在变体无人机上的应用得到国内外的广泛研究。早在2001年NASA的I-2000充气机翼无人机由母机携带进行了投放试飞试验,并成功在空中充气展开机翼、滑翔返回地面[1-2]。美国Kentucky大学、ILC Dover试验室对拉筋式充气机翼进行了风洞试验研究和飞行试验[3]。国内有西北工业大学进行了充气机翼的设计、试验研究和飞行试验并取得成功[4]。北京航空航天大学进行了充气机翼的承载能力试验并对其气动特性进行了仿真分析[5]。哈尔滨工业大学对空间薄膜结构和充气锥台等结构展开了褶皱分析[6-7]。但目前考虑气弹耦合效应,对充气机翼进行计算和对比试验分析的文章还比较少。
本文针对充气机翼在气动载荷下的褶皱和失稳问题,在经典工程梁理论的基础上,计入薄膜褶皱引起的刚度退化效应,建立了充气悬臂机翼的等效梁模型,并耦合基于片条理论的气动力计算方法,开展了充气悬臂机翼的静气弹行为研究,获得了充气机翼的许用包线范围,并通过试验验证了计算结果,预测了所设计充气机翼的静气弹许用范围。
1 充气机翼的弯曲变形及褶皱分析
1.1 褶皱分析
本文研究对象为一采用NACA0020为模板设计的充气悬臂机翼。所设计的充气机翼截面如图1(a)所示,通过13根维形筋条分隔成14个气室[8]。图中:R为薄膜单元所在气室的曲率半径;αeff为有效迎角;Veff为有效速度。机翼的尺寸和材料参数如表1所示, 制作完成的悬臂机翼如图1(b)所示。
机翼的表面薄膜承受充气压力产生的展向和弦向张力。受弯矩作用时,机翼上下表面展向张力发生变化,形成截面内力矩,使得充气机翼具备一定的抗弯能力。机翼内部筋条充气后受拉,用以维持翼型,所形成的多气室类似于经典机翼的多闭室,可传递剪流,使得充气机翼具备一定的抗扭能力。
根据机翼截面的几何特征,计算得到截面形心位于48%弦长处,即截面刚心和机翼弹性轴所在位置,如图1所示。
充气机翼弯曲时,受压面可能发生褶皱并引起刚度退化。充气机翼的褶皱判据采用充气悬臂管褶皱分析[9]中所采用的判据。

图1 悬臂充气机翼及截面形状Fig.1 Cantilever inflated wing and its cross-sectional shape
表1 充气机翼的尺寸和材料参数Table 1 Size and material parameters of inflated wing
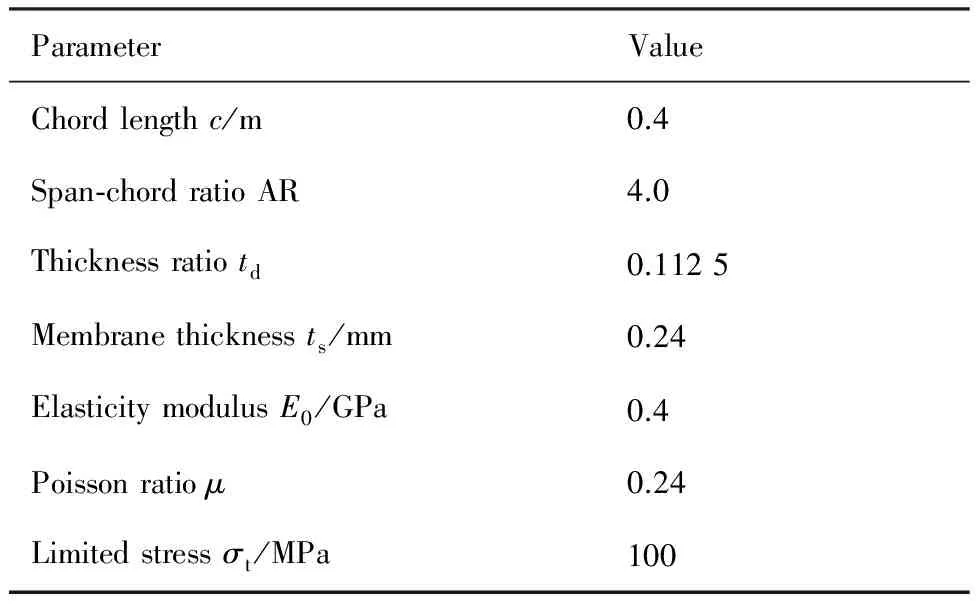
ParameterValueChordlengthc/m0.4Span⁃chordratioAR4.0Thicknessratiotd0.1125Membranethicknessts/mm0.24ElasticitymodulusE0/GPa0.4Poissonratioμ0.24Limitedstressσt/MPa100

(1)
(2)
(3)
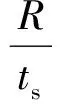
(4)
式中:p为充气压力;A为机翼截面的轮廓包围面积;Awalls为机翼截面的薄膜截面面积;MX和MZ分别为单元体所在截面绕X轴和Z轴方向的弯矩;IXX和IZZ分别为截面对X轴和Z轴的惯性矩;x和z分别为薄膜单元在截面坐标系中的坐标值(图1(a))。

图2 薄膜单元体应力组成Fig.2 Stress components of membrane element
单元体的切应力τYH通过计算该处截面闭室剖面剪流得出[11],剪流的表达式为
(5)
(6)
(7)

(8)
式中:q为整个截面剪流分布;QX和QZ分别为截面上沿X轴和Z轴方向的剪力;SX和SZ分别为截面关于X轴和Z轴的静矩;Ω为截面面积A的两倍;MY为截面上绕Y轴方向上的扭矩;ρ为ds段上剪力到原点的垂直距离。由于机翼为直机翼,不考虑弯扭耦合效应。在纯弯时,MY=0。
按迭加原理,MX和MZ的作用可以分别进行考虑。这里为便于理解,仅讨论MX作用的情况。MZ作用时的处理方法与此类似,不过通常IZZ远大于IXX,且MZ小于MX,因此MX的作用可忽略不计。机翼截面没有发生褶皱时,整个截面具有承压能力,展向应力σY在Z轴方向上连续线性分布,分布示意如图3所示。

图3 未褶皱截面σY分布示意图Fig.3 Distribution of σY over unwrinkled section
未褶皱截面σY分布表达式可写为

(9)
当截面发生局部褶皱时,褶皱区域不具备承压能力,展向应力σY重新分布,且假设由最大应力到最小应力呈线性分布,如图4所示。

图4 褶皱截面σY分布示意图Fig.4 Distribution of σY over wrinkled section
褶皱截面σY分布的表达式为
(10)
σY分布满足轴向力平衡和力矩平衡
pA=∮sσYtds
(11)
联立式(10)和式(11)可求得截面展向应力的重新分布。
确定截面上各单元体的应力分量后,单元体的主应力为
(12)
式中:σ1和σ2分别为单元体最大和最小主应力。单元体发生褶皱的判断条件为
(13)
1.2 弯曲变形
分析充气机翼的静变形时采用微分求积法[12],将其视为一根位于机翼弹性轴处的悬臂梁,如图5所示,E.A.表示弹性轴所在的位置,A.C.表示气动力作用中心轴,L.E.表示前缘,T.E.表示后缘。在机翼根部建立根部坐标系ORXRYRZR, 在机翼展向切片上定义局部坐标系OSXSYSZS。悬臂梁上各点的截面惯性矩等于充气机翼对应截面的惯性矩。

图5 充气机翼的简化悬臂梁模型Fig.5 Simplified cantilever beam model of inflated wing
当机翼发生弯曲褶皱时,截面上的褶皱区不具备承受压应力的能力,如图4所示。假设机翼弯曲过程中截面刚心位置不变,计算截面惯性矩I时除去图中褶皱区虚线部分面积。此时I值减小,材料模量E保持不变,截面刚度EI减小。沿Y轴取一系列截面计算其惯性矩I(y),以此代表轴向变刚度的简化悬臂梁。
若在悬臂梁端部施加Z轴方向的集中力F,则Y轴上任意截面受到的弯矩为
MX=F(AR·c-y)
(14)
当梁发生弯曲变形时,梁上任意一点y处的挠度为w,挠曲线的近似微分方程可表示为
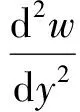
(15)

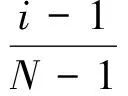
(16)
式中:N为网点总数;ξi为网点的坐标值。
考虑一维函数W(ξ)在区间[0,1]上连续可微,则函数W(ξ)的r阶偏导数在第i个离散点的微分求积法逼近公式为
(17)
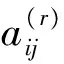
(18)
对式(15)进行微分求积得到
(19)
1.3 建模计算
以图1(b)所示的悬臂机翼为分析对象,开展了相应的机翼弯曲试验和计算对比分析,以检验上述算法的有效性。
所建立的充气悬臂机翼弯曲试验系统如图6所示。充气机翼的根部插入铝质支座内,并用胶水粘贴在支座上,实现根部固支。通过减压阀和压力传感器保持机翼充气压力稳定。在翼尖截面刚心处施加砝码代表集中力F,不产生扭转。通过标尺测量翼尖的竖向位移w。
在MATLAB中建立上述充气悬臂机翼的简化悬臂梁模型。在机翼自由端施加竖直向下的集中力F,弹性轴上取11个网点进行微分求积计算挠度。为了精确估计起皱区,截面应力计算时在机翼展向分为100个截面,每个截面沿轮廓线分为2 000个单元体。
充气压力p=40 kPa时,计算得机翼根部下表面起皱区随载荷增加的变化情况如图7所示。

图6 充气机翼弯曲试验系统Fig.6 Bending test system of inflated wing

图7 p=40 kPa 时机翼下表面起皱区计算结果 Fig.7 Calculated wrinkle area on lower skin of wing at p=40 kPa
当p=40 kPa时机翼下表面褶皱区的实测拍摄照片如图8所示。
为便于观察,图8中用红线标示出了显著的可观褶皱。需要说明的是图8(a)中黑线以外区域出现了几道囊布局部凹陷,主要是由于气囊布粘贴时囊布对接不平顺所带来的初始褶皱缺陷。加载所带来的褶皱,首先出现在根部机翼截面高度最大的地方。截面高度最大地方所对应的囊布片条上,褶皱区随载荷的增加扩展也最快。这些规律与理论分析一致。对比图7和图8可见,计算起皱区基本与试验起皱区相吻合,两者展向起皱范围的扩展基本相同,但实测弦向起皱范围的扩展略大于计算情况,应与初始褶皱缺陷的存在有关。
图9进一步给出了充气压力分别为40、60、80、100 kPa时,计算和试验获得的翼尖位移w随载荷F的变化曲线。由图9可知,在刚刚发生褶皱时机翼并没有完全失去承载能力,起皱后刚度损失导致载荷-位移(F-w)曲线斜率减小,计算曲线体现出了这一趋势。对比分析起皱点处的计算值与试验值,最大相对误差为-8.2%,且充气压力较大时,趋于稳定,如60 kPa充压工况时起皱点的计算误差为2.1%,80 kPa充压工况时为3.2%。这一结果验证了本文所建立的充气机翼变形计算方法是精确的。

图8 p=40 kPa 时机翼下表面起皱区试验结果Fig.8 Measured wrinkle area on lower skin of wing at p=40 kPa

图9 F-w计算曲线与试验曲线的比较Fig.9 Comparison of F-w curves obtained by calculation and test
另外,根据试验与计算之间的对比,本文总结出一个判断充气机翼弯曲失效的经验判据:当根部褶皱区沿机翼展向扩展到机翼总根弦的60%时,机翼发生弯曲失稳。根据这一判据,可确定当前加载方式下,机翼的失效载荷如表2中第2列所示,该载荷所对应的机翼自由端测试挠度we和计算挠度wc分别如表2中第3列和第4列所示,两者相对误差小于4%。验证了充气机翼弯曲挠度计算方法的正确性。
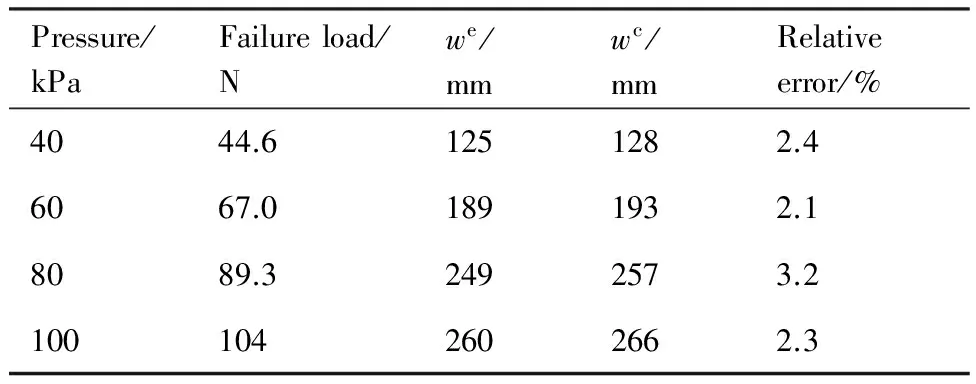
表2 失效载荷与弯曲变形Table 2 Failure load and deflection
2 充气机翼许用包线的确定
2.1 气动力模型
在上述简化悬臂梁模型基础上,根据片条理论建立气动力模型[12]。如图5所示,在机翼根部建立根部坐标系ORXRYRZR,坐标原点位于机翼根部截面刚心。根据片条理论,机翼可离散为附连在等效弹性轴上的沿展向分布的一排切片,每个切片代表一段二维翼型,仅考虑切片绕YR轴的扭转刚度和绕XR轴的弯曲刚度。对于直机翼,面内弯曲刚度相对较大,可忽略不计。
在机翼展向切片上定义局部坐标系OSXSYSZS,用以计算切片当地风速和气动力。设机翼初始状态迎角为α,来流速度矢量为VR,对于机翼根部坐标系有
(20)
(21)
(22)
对于弹性轴上任意切片,当地风速为
VS=DR→SVR
(23)
(24)
式中:DR→S为根部坐标系到局部坐标系的转换矩阵,其表达式为
(25)
其中:φ和θ分别为切片在根部坐标系下绕XR轴的弯曲角和绕YR轴的扭转角。在每一个切片上,1/4弦线处的升力和阻力为
L=qDcCL ααeff
(26)

(27)
其中:qD为当地动压;CLα为升力系数斜率,翼尖效应忽略不计。
风轴系下的升力和阻力通过转换矩阵转换成弦向的力C和垂直于弦向的力N,即
(28)
式中:DL→S为从风轴系到当地局部坐标系的转换矩阵。
则弹性轴上y0处切片的空气动力总和F(y0)可由[y0,l]区间内切片的空气动力积分得到
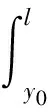
(29)
同理,y0处切片的气动弯矩可表示为
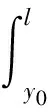
[Dy1→y0(r(y1)-r(y0))]dy1
(30)
式中:Dy1→y0为y1处切片局部坐标系到截面y0处切片局部坐标系的转换矩阵,计算方法同DL→S和DR→S;r(y0)和r(y1)分别为切片y0和切片y1在根部坐标系下刚心位置的坐标值。
根据悬臂梁挠曲计算公式,力矩和变形之间的方程为
(31)

2.2 静气弹变形的迭代算法
式(31)建立了气动力与结构静变形之间的耦合方程,其中结构截面惯性矩随着褶皱的扩展会发生变化。这一耦合方程需要采用迭代策略进行求解,
本文建立的迭代求解流程如图10所示。输入机翼的结构参数(见表1)和充气压力。在计算应力和褶皱时机翼被分割成100个片段。在计算结构变形时,机翼等效梁分为10个片段共计11个微分求积网格点,相应的气动力分成10个片条进行计算。给定来流动压、迎角和升力系数(保守取为2π),则可根据片条理论计算机翼的初始气动力。根据初始气动力分布,可以计算初始扭转角和初始弯曲变形。将初始扭转角和初始迎角叠加后构成新的有效迎角,重新计算气动力,再迭代计算机翼的变形。迭代直到收敛判据满足。迭代收敛判据定义为梁自由尖端两次计算的位移差小于0.01 mm。如计算过程中机翼发生褶皱,则在机翼变形计算迭代的过程中还需如1.3节所述类似,迭代计算截面应力的重分配,确定截面弯曲刚度的等效退化量。
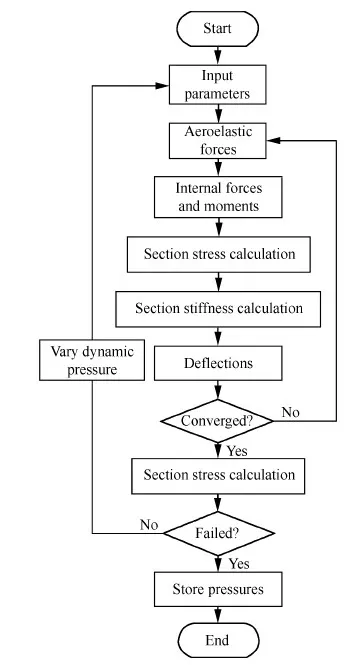
图10 迭代算法流程图Fig.10 Flowchart of iteration method
计算收敛后,判断翼面的应力状态,若达到临界失效判据,则机翼失效,计算停止。若没有失效,则增大动压重新计算。判断充气机翼是否失效,需同时考虑两个方面的判据。第一个判据为机翼囊布是否发生开裂破坏。充气机翼在气流作用下受到气动升力和阻力的作用,机翼弯曲受拉面的囊布应力最大。当局部囊布的最大主应力超过囊布开裂极限应力σt时,囊布发生不可逆的开裂破坏。机翼囊布发生开裂破坏的应力临界条件(I)为σ1=σt。机翼褶皱失稳是充气机翼的另一种失效模式,褶皱失稳出现在机翼的弯曲受压面。如第1节所述,机翼发生初始褶皱还有一定承载能力,因此可设立两个褶皱失效临界条件进行比较分析:刚刚发生褶皱(II)和根部褶皱区沿机翼展向扩展到机翼总根弦的60%时机翼发生褶皱失稳(III)。
2.3 算法验证
采用上述的迭代算法,计算图7所示充气机翼在20 kPa充气压力下,分别以(II)和(III)判据作为临界条件计算获得充气机翼发生初始起皱和褶皱失效时的临界动压-迎角曲线如图11所示。图12给出了机翼迎角为1.8°,充气压力为20 kPa,来流动压为571 Pa时,机翼尖端位移随迭代次数增加稳定收敛的过程。

图11 p=20 kPa下的失效包线Fig.11 Failure envelope at p=20 kPa

图12 翼尖位移迭代收敛过程 Fig.12 Iteration convergence process of wing tip displacement
为检验以上计算的准确性,以风洞试验获得的充气机翼皱褶失效数据作为依据进行验证。充气机翼在风洞中的安装状态如图13所示,试验中充气压力p=20 kPa,迎角α0=1.8°。试验结果表明:充气机翼的起皱临界风速为29 m/s,对应的实测动压为477 Pa;褶皱失稳临界风速为33 m/s,对应实测动压为608 Pa。机翼根部褶皱扩展过程如图14所示。

图13 充气机翼的安装状态Fig.13 Inflated wing installed in tunnel

图14 试验中充气机翼的褶皱扩展过程Fig.14 Wrinkle developing process of inflated wing by test

图15 计算得到的充气机翼褶皱扩展过程 Fig.15 Wrinkle extending process of inflated wing by simulation
分析图11可知,α0=1.8°时,计算得到的起皱临界动压为480 Pa,与实测起皱临界动压相差0.6%;图15给出了计算得到的充气机翼褶皱扩展过程,结果表明,当风速达到实测褶皱失稳风速33 m/s(实测失效动压为608 Pa)时,计算获得的褶皱区扩展如图15(c)所示,根部褶皱扩展区已达到了机翼总根弦的70%;若以前文确定的(III)判据进行失稳动压确定,即以褶皱占机翼总根弦的60%为判据,计算临界机翼褶皱失稳动压为571 Pa,与实测值之间的相对误差为6%,计算判据相对保守。
2.4 充气机翼许用包线确定
计算流体力学(CFD)分析表明,本文所设计充气机翼翼型的失速迎角为17°。由于同等动压下,迎角越大气动载荷越大,充气机翼的许用包线将越窄,因此本文此处仅计算机翼最大许用迎角为15°时的许用包线。
将充气机翼沿展向分为50个切片,分别以临界条件(I)~(III)作为失效判据,计算获得对应3个判据的的3条包线,如图16所示。以曲线(I)、(III)所示包线为例。曲线(I)以上区域表示机翼该状态下将发生破坏失效,曲线(III)以下区域表示机翼将发生褶皱失效,曲线(I)和曲线(III)之间所包围的区域表示机翼的安全使用范围,不会发生失效行为。

图16 充气机翼的许用包线Fig.16 Available envelope of inflated wing
曲线(II)确定的许用范围小于曲线(III)。就临界条件(II)而言,在迎角为15°时,最大许用动压分别为489 Pa,所对应的许用充气压力为167 kPa。就临界条件(III)而言,最大许用动压为581 Pa,对应充气压力为137 kPa。可以预计,如果进一步增大充气机翼的展弦比,最大许用动压会减小,对应充气压力也有所减小。
3 结 论
1) 建立了充气机翼的变形起皱分析方法,有效地将褶皱充气机翼等效处理为刚度随褶皱扩展逐步退化的变截面梁,并且可根据翼面应力分布预测褶皱的扩展。充气机翼模型静力试验测得的翼稍变形、褶皱区扩展及临界失效载荷与计算分析结果保持良好一致性,验证了所提出的充气机翼起皱判据、失效判据和所构建褶皱扩展和变形预测方法的有效性。
2) 论文建立了耦合机翼气动力的充气机翼静气弹变形迭代计算方法。计算结果与风洞试验结果的对比表明,计算获得的机翼临界失效动压与实测临界失效动压之间的误差不超过6%,验证了所构建充气机翼静气动弹性耦合分析模型的有效性。运用该模型,在动压-充气压力(q-p)平面上确定了所制作充气机翼的静气弹许用包线。
[1] PAHLE J W, THOMTON S V, VOGUS S, et al. Ground and flight evaluation of a small-scale inflatable-winged aircraft[C]//40th AIAA Aerospace Sciences Meeting & Exhibit. Reston: AIAA, 2002.
[2] USUI M, SIMPSON A, SMITH S, et al. Development and flight testing of a UAV with inflatable-rigidizable wings[C]//42nd AIAA Aerospace Sciences Meeting and Exhibit. Resston: AIAA, 2004.
[3] USUI M, JACOB J D, SMITH S W, et al. Second generation inflatable/rigidizable wings for low-density flight applications[C]//46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2005: 1-9.
[4] 吕强, 叶正寅, 李栋. 充气结构机翼的设计和试验研究[J]. 飞行力学, 2007, 25(4): 77-80.
LV Q, YE Z Y, LI D. Design and capability analysis of an aircraft with inflatable wing[J]. Flight Dynamic, 2007, 25(4): 77-80 (in Chinese).
[5] 王伟, 王华, 贾清萍. 充气机翼承载能力和气动特性分析[J]. 航空动力学报, 2010, 25(10): 2296-2303.
WANG W, WANG H, JIA Q P. Analysis on bearing capacity and aerodynamic performance of an inflatable wing[J]. Journal of Aerospace Power, 2010, 25(10): 2296-2303 (in Chinese).
[6] 王长国, 杜星文, 赫晓东. 空间充气薄膜结构的褶皱分析[J]. 力学学报, 2008, 40(3): 331-338.
WANG C G, DU X W, HE X D. Wrinkling analysis of space inflatable membrane structures[J]. Chinese Journal of Theoretical and Applied Mechanics, 2008, 40(3): 331-338 (in Chinese).
[7] 杜振勇, 王长国, 谭惠丰. 受弯充气锥台的褶皱特性分析[J]. 工程力学, 2011, 28(7): 73-78.
DU Z Y, WANG C G, TAN H F. Wrinkle characteristic analysis of a conical inflated cantilaver beam under bending[J]. Engineering Mechanics, 2011, 28(7): 73-78 (in Chinese).
[8] 朱亮亮, 叶正寅. 充气式机翼的通用设计方法[J]. 空军工程大学学报(自然科学版), 2009, 10(5): 16-21.
ZHU L L, YE Z Y. Research on a universal design method for inflatable wings[J]. Journal of Air Force Engineering University (Natural Science Editioin), 2009, 10(5): 16-21 (in Chinese).
[9] 陈帅, 李斌, 杨智春. 充气悬臂梁的弯曲失效行为[J]. 工程力学, 2010, 27(S1): 299-304.
CHEN S, LI B, YANG Z C. Benging-collapse behavior of an inflatated circular-cylindrical cantilever beam[J]. Engineering Mechanics, 2010, 27(S1): 299-304 (in Chinese).
[10] GALROM Y C, RAVEH D E. Simplified aerostructural static model for inflated wings[J]. AIAA Journal, 2011, 49(6), 1180-1190.
[11] 黄其青,王生楠. 结构力学基础[M]. 西安: 西北工业大学出版社,2002: 90-115.
HUANG Q Q, WANG S N. Foundation of structural mechanics[M]. Xi’an: Northwestern Polytechnical University Press, 2002: 90-115 (in Chinese).
[12] 聂国隽, 徐敏, 仲政. 轴向变刚度矩形截面梁的弹性及弹塑性弯曲[J]. 中国科学: 物理学力学 天文学, 2011, 41(1): 86-93.
NIE G J, XU M, ZHONG Z. Elastic and elasto-plastic bending of rectangular beams with variable stiffness along axial direction[J]. Scientia Sinica (Physica, Mechanica & Astronomica), 2011, 41(1): 86-93 (in Chinese).
李斌男,博士,教授,博士生导师。主要研究方向:结构动力学与控制。
Tel.: 029-88493386
E-mail: leebin@nwpu.edu.cn
URL:www.cnki.net/kcms/detail/11.1929.V.20160317.1257.004.html
Wrinklingandfailurebehaviorresearchofinflatedwing
LIBin*,DONGNannan,FENGZhizhuang,NIUWenchao
SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China
Basedonclassicalengineeringbeamtheory,combinedwiththestressstateanalysisoftensemembrane,thewrinklingandinstabilitycriterionsofinflatedwingareproposed.Weconsiderstiffnessdegradationcausedbywrinkleofinflatedwing,andtreattheinflatedwingasabeamwhichpossessesavariablesectionstiffnesswiththeexpansionofwrinkle;anequivalentbeammodelofinflatedwingisestablished,andthedifferentialquadraturemethodisappliedtocalculatethebendingdeformationofinflatedwing.Thecalculatedresultsareconsistentwiththeexperimentalresultsfromthestaticbendingtestsofinflatedwing,andhenceverifytheeffectivenessoftheproposeddeformationanalysismethodofinflatedwing.Weusethestriptheorytointroducetheaerodynamicmodelwhichisthencoupledwiththeequivalentbeammodelofinflatedwing,andthusastaticaeroelasticmodelofinflatedwingisdeveloped,whichappliesaniterativemethodtosolve.Accordingtothewrinklingandinstabilitycriterions,weusetheproposedmodeltocalculatethecriticalwrinkledynamicpressureandcriticalinstabilitydynamicpressureoftheexperimentalinflatedwing,andtheobtainedresultsareconsistentwiththeresultsfromtunneltests.Furthermore,theproposedmodelisusedtopredicttheextendingprocessofmembranewrinkledzoneandbendingfailureloadfortheinflatedwing,andthenobtaintheavailablestaticaeroelasticenvelopecurvesofinflatedwingunderdifferentcriterionconditions,andprovidenecessarysafetyboundaryanalysisforthedesignofinflatedwing.
inflatedwing;wrinkle;variablestiffness;staticaeroelasticity;instablility
2015-10-20;Revised2016-01-06;Accepted2016-02-29;Publishedonline2016-03-171257
s:NationalNaturalScienceFoundationofChina(11172238);TheFundamentalResearchFundsfortheCentralUniversities(3102014KYJD015); “111”project(B07050)
.Tel.:029-88493386E-mailleebin@nwpu.edu.cn
2015-10-20;退修日期2016-01-06;录用日期2016-02-29; < class="emphasis_bold">网络出版时间
时间:2016-03-171257
www.cnki.net/kcms/detail/11.1929.V.20160317.1257.004.html
国家自然科学基金 (11172238); 中央高校基本科研业务费专项资金 (3102014KYJD015); 高等学校创新引智计划 (B07050)
.Tel.:029-88493386E-mailleebin@nwpu.edu.cn
李斌, 董楠楠, 冯志壮, 等.充气机翼的褶皱和失效行为研究J.航空学报,2016,37(10):3044-3053.LIB,DONGNN,FENGZZ,etal.WrinklingandfailurebehaviorresearchofinflatedwingJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3044-3053.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0056
V216
A
1000-6893(2016)10-3044-10

