基于极值理论的平尾结冰飞行风险评估
王健名, 徐浩军, 薛源, 王小龙, 李哲
空军工程大学 航空航天工程学院, 西安 710038
基于极值理论的平尾结冰飞行风险评估
王健名, 徐浩军*, 薛源, 王小龙, 李哲
空军工程大学 航空航天工程学院, 西安 710038
提出了结合极值理论与Copula模型来量化评估平尾结冰条件下飞行风险概率的方法。通过建立人-机-环复杂系统模型,对平尾在进近与着陆过程中的结冰情形进行仿真,采用蒙特卡罗法提取平尾结冰极值参数,验证了所提取极值参数符合一维广义极值(GEV)分布,根据飞行风险的定义和相关安全性准则,建立了平尾结冰飞行风险发生的判定条件,计算得出一维极值飞行风险概率;在此基础上选取Copula模型来描述二维极值参数的相关性,对多种Copula模型的未知参数进行辨识,通过拟合优度检验对精度进行验证,得出Joe Copula模型对二维极值分布的描述最为准确,运用Joe Copula模型计算出二维极值飞行风险概率,有效解决了一维极值具有的局限性。所提方法对飞行安全评估等理论有一定参考价值,能为平尾结冰飞行事故的预防提供分析和检验依据。
极值理论; Copula模型; 平尾结冰; 飞行风险概率; 蒙特卡罗法; 参数辨识
飞机飞行时,常常会产生平尾结冰现象,导致平尾气动特性被破坏,平尾负升力减小,配平能力下降,升降舵操纵效率降低。当平尾结冰发生在进近与着陆过程中时,飞机极易发生平尾失速现象,甚至导致飞行事故发生。目前,平尾结冰已成为世界较为关注的安全隐患问题,评估在平尾结冰条件下的飞行风险概率显得极其重要。
国外最早对飞机平尾结冰现象进行研究。包括风洞试验和飞行测试,如1994年NASA和FAA联合研究的平尾结冰项目Tailplane Icing Program(TIP),其以DHC-6为试验机型,进行了一系列平尾结冰飞行试验和风洞试验,得到了大量的试验数据[1-2];通过计算流体力学(CFD)的应用,进行水滴运动和撞击特性计算、冰形预测以及分析平尾结冰后的气动参数变化[3-5];对平尾结冰进行飞行仿真,分析平尾结冰对飞机动力学特性和飞行品质的影响[6-7];进行相应的结冰控制和防、除冰方法与装置的研究[8-10],如1998年首次提出了飞机智能防冰系统(Smart Icing System, SIS)等。
与国外相比,国内关于平尾结冰方面的研究起步较晚,主要在以下方面进行了一定的相关性研究:对平尾结冰飞机纵向气动参数进行辨识,定量地分析了平尾结冰对飞机纵向气动参数的影响[11];通过研究平尾结冰导致的飞行事故,分析了平尾结冰对平尾气动特性的影响,给出预防平尾失速的方法[12];预测结冰外形、结冰边界保护以及防除冰[13-15]等。
但综合国内外来看,关于平尾结冰条件下的飞行风险概率评估方面的研究极少。而国军标GJB900-90[16]、SAE-ARP-4761[17]、MIL-HDBK-516B[18]及MIL-STD-882D[19]等安全性规范考虑飞行过程中的不确定性和随机性因素较少,较难对多因素耦合、非线性较强的飞行条件进行飞行风险量化预测,尤其是在进近与着陆过程中平尾结冰的条件下。因此,迫切需要建立有效的理论与方法来定量评估平尾结冰条件下的飞行风险概率。鉴于此,本文提出了一种基于人-机-环复杂系统建模仿真和极值理论[20]提取相应极值参数,利用Copula模型来量化评估飞行风险概率的方法。此方法对研究平尾结冰引起的飞行安全和适航性问题具有重要意义。图1为本文飞行风险评估流程图。

图1 飞行风险评估流程Fig.1 Flowchart of flight risk evaluation
1 平尾结冰后人-机-环复杂系统建模
平尾结冰的内外部影响因素具有复杂随机性的特点:一是复杂的非线性物理特性,主要指驾驶员和飞机在解析模型中的非线性;二是复杂的随机性,主要指外部天气变化、驾驶员操纵行为差异以及航空设备故障发生等。考虑到驾驶员、飞机和平尾结冰环境之间的相互耦合及相互作用的复杂关系,本文分别建立了驾驶员模型、飞机运动模型和平尾结冰参量模型,实现平尾结冰动力学仿真。
1.1 驾驶员模型
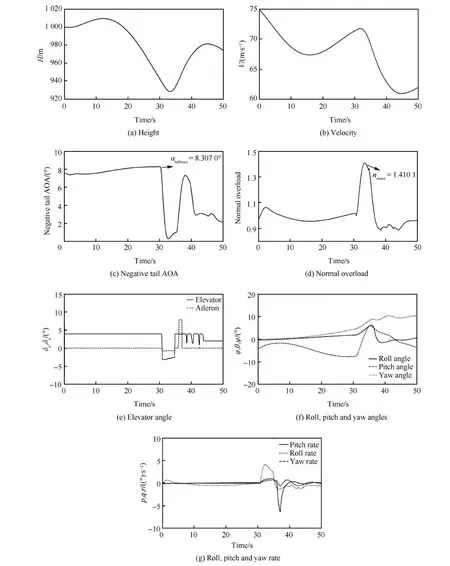
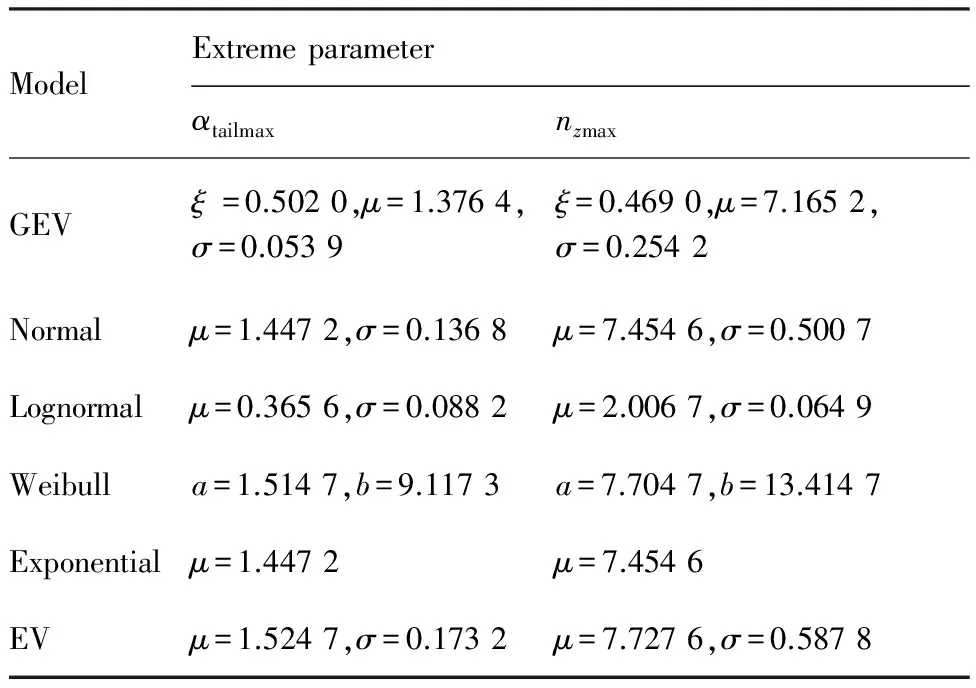
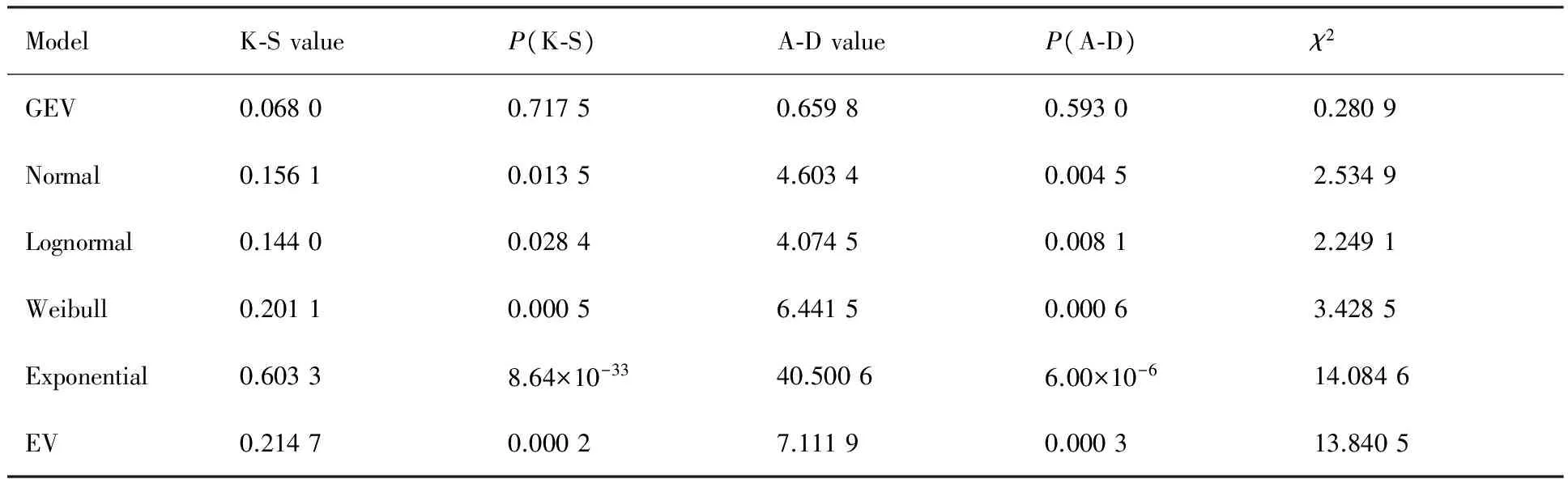
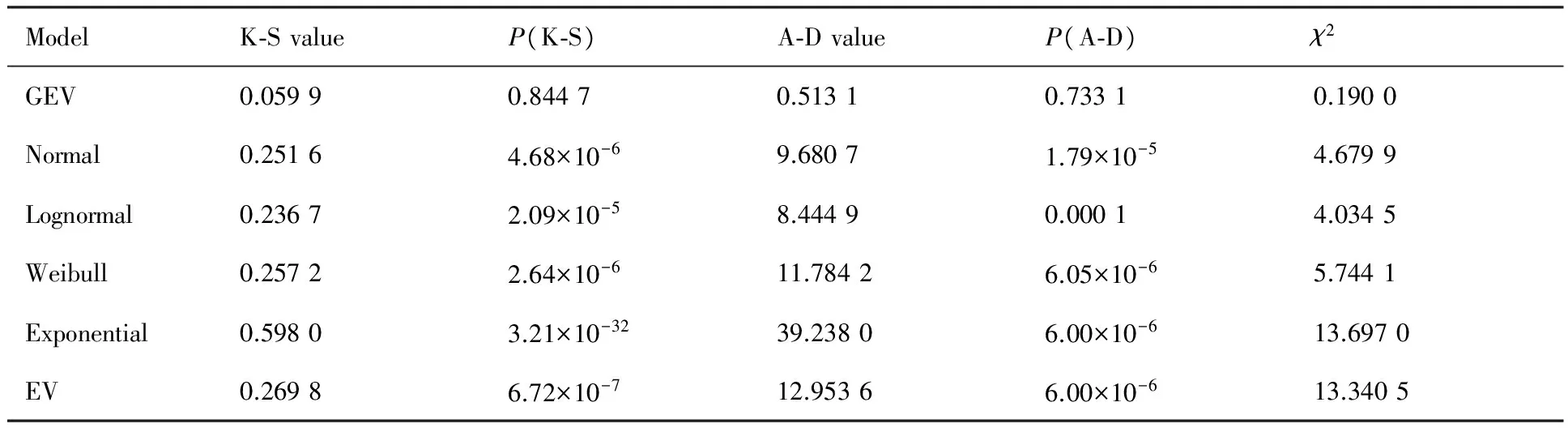
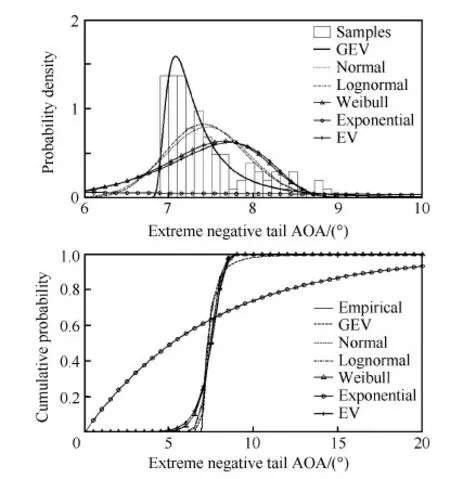
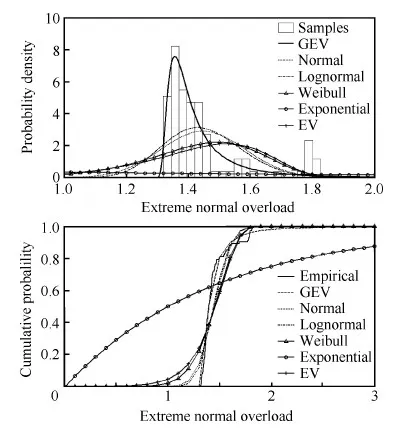
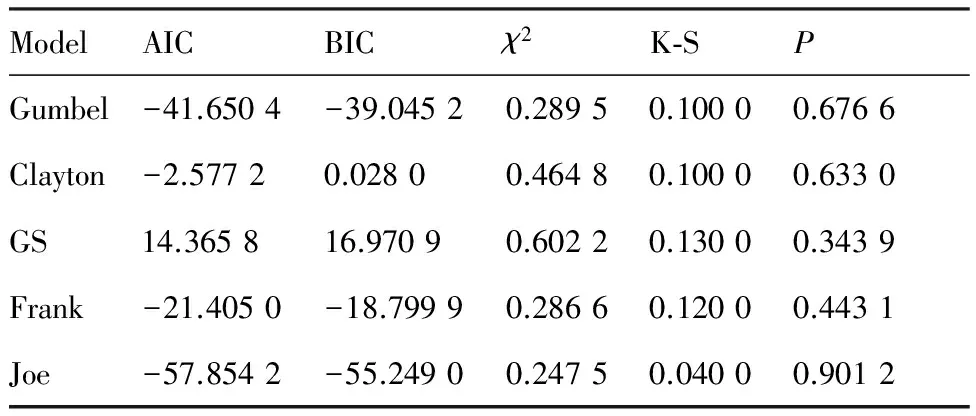
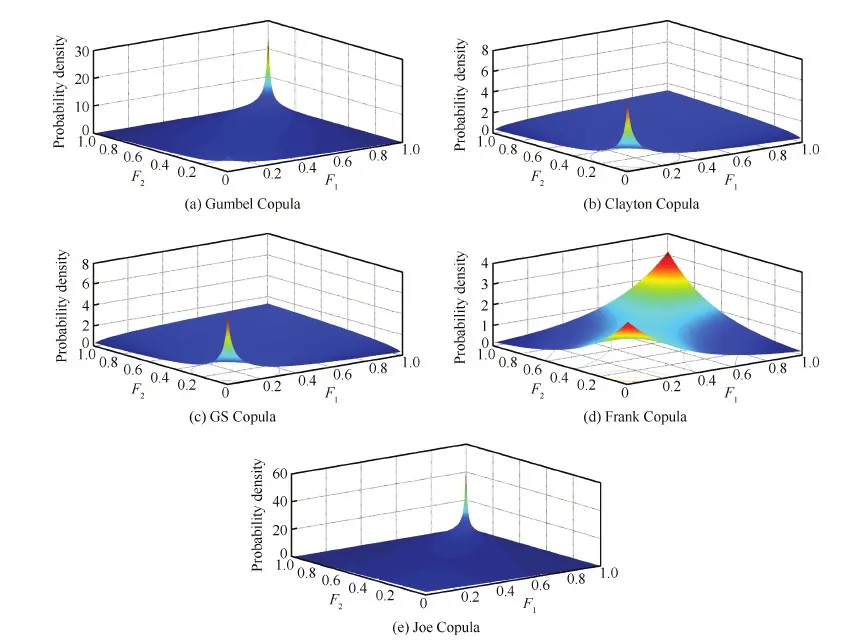
平尾结冰后,驾驶员的操纵对飞机影响极大,因此驾驶员模型是评估平尾结冰飞行风险需考虑的重要因素。本文将驾驶员的操作分为3个阶段。当t 图2 驾驶员补偿模型Fig.2 Compensation model of pilot 则驾驶员模型的输入输出关系可以表示为 (1) 平尾结冰会导致平尾负升力减小,升降舵效率降低,使得飞机配平能力减弱,进而会使飞机转入俯冲状态,若驾驶员不及时调整升降舵,飞机可能会发生飞行事故。以升降舵为例,取俯仰角为信号,建立升降舵运动的非线性模型(副翼运动的非线性模型与之相似,在此不再赘述): (2) 式中:t0为驾驶员开始操纵升降舵的时刻;Δt为偏转所需时间;δe0为初始升降舵偏角;Vδe为升降舵偏转速率;tp为延迟时间,主要包括驾驶员操纵过程中的固有延时特性、肌肉神经滞后时间以及飞行参数传递和处理过程中的滞后时间等。 假设驾驶员操纵升降舵的偏转速率Vδe服从均匀分布,其概率密度函数为 (3) 式中:a和b分别为升降舵偏转速率的最小值和最大值。 1.2 基于四元数法的飞机运动模型 基于四元数法构建飞机本体的六自由度运动模型为 (4) (5) (6) (7) (8) (9) c1=(Iyy-Izz)Izz-IxzIxz/λI c2=(Ixx-Iyy+Izz)Ixz/λI c3=Izz/λI c4=Ixz/λI c5=(Izz-Ixx)/Iyy c6=Ixz/Iyy c7=1/Iyy c8=[(Ixx-Iyy)Ixx+IxzIxz]/λI c9=Ixx/λI λI=IxxIzz-IxzIxz 1.3 平尾结冰参量模型 采用平尾结冰后的气动参数模型[6]: (10) (11) 式中:KCA为气动导数对结冰的敏感性,只与飞机有关而与气象条件无关,对于给定的飞机是常值。η和ηice相似,只是采用实际飞机平尾气动弦长和相应飞行速度进行计算。它是关于大气温度、液态水含量、水滴直径、结冰遭遇时间等的函数,只与气象条件有关,与具体飞机无关。 由式(10)和式(11)可得 C(A)iced=1+ηKCAC(A) (12) 此结冰气动导数的计算公式是通过NASA对双水獭飞机进行结冰飞行试验研究,由Bragg等提出的,通过结冰后气动导数下降比例和结冰严重影响程度η表征飞机受结冰影响。文献[21]通过试飞验证了此模型在Cessna 208B飞机上同样适用,因此模型具有较高的适用性。本文亦采用此模型。 本文进行的平尾结冰飞行风险概率评估是基于飞机在进近与着陆过程中,平尾发生结冰导致平尾临界负失速迎角减小(平尾临界失速迎角增大),平尾负升力降低,飞机进入俯冲状态,进而引起飞行风险来展开研究的。 研究此科目内外部影响因素需要大量数据,试飞与人在回路地面试验都无法达到此数据量;并且飞机在进近与着陆过程中的平尾结冰飞行风险评估属于高风险科目,飞行风险大,需模拟的外部环境等条件又十分困难。因此,如何利用有限数据量对平尾结冰飞行风险进行量化评估是一个难点。本文通过建立平尾结冰后的人-机-环复杂系统模型,利用极值理论,基于蒙特卡罗法提取相应飞行参数极值,能较好地解决上述问题。 2.1 飞行极值参数提取 仿真共有3个数据库,分别是驾驶员模型数据库、平尾结冰数据库和外部环境数据库。驾驶员模型数据库:驾驶员个体具有不同的操纵习惯、心理状态和身体素质,使得驾驶员在应对新环境时表现出操纵行为的差异性,通过采集飞行员的实验操纵数据,辨识了驾驶员模型中的未知参数,主要包括驾驶员操纵过程中的固有延时特性,肌肉神经滞后时间以及飞行参数传递和处理过程中的滞后时间等,从而建立驾驶员操纵行为数据库;平尾结冰数据库:考虑到本文飞机气动结构与DHC-6相近,故仿真利用DHC-6平尾结冰数据;外部环境数据库:主要包括空气密度、当地气压、离散突风、风切变状况、雨雪状况和空气湿度等。 基于蒙特卡罗法提取出相应飞行极值参数过程如图3所示,具体步骤如下: 1) 设定飞机初始飞行状态。初始飞行高度、速度、姿态角、结冰时间等。 2) 将由天气状况得到的云层液态水含量(LWC)、平均有效水滴直径(MVD)、温度T,在平尾结冰数据库中进行蒙特卡罗抽样,提取平尾结冰数据的随机变量值,将其作为检索条件,结合设定的结冰时间,依据统计数据从平尾结冰数据库中提取出平尾结冰严重程度η,其值是一个常值。 3) 从外部环境数据库中进行蒙特卡罗抽样,提取外部环境影响因素的随机变量值。 4) 从驾驶员模型数据库中进行蒙特卡罗抽样,提取驾驶员操纵行为参数的随机变量值。 5) 进行第i次飞行仿真计算。 飞机本体方程为基于四元数的六自由度方程,采用四阶龙格库塔微分算法。实时仿真计算机通过相应飞控系统转化的C代码进行实时仿真,仿真时间步长为0.02 s。 6) 记录第i次计算结果中的飞行参数,提取飞行参数极值,存入数据库。 7)i=i+1,返回到步骤2),循环迭代到i=n结束。 n为蒙特卡罗计算次数,n越大越能反应极值的统计特性,但n太大会又会导致计算任务增加。经验证当n>2 000时,计算结果趋于稳定,因此本文选取n=2 000。 图3 飞行极值参数的提取过程Fig.3 Process of extracting flight extreme parameters 图4以第56次飞行仿真计算为例,表征说明飞行仿真及参数极值提取的过程,仿真是在初始高度H=1 000 m(机场高度500 m),速度V=75 m/s,飞机遭遇平尾结冰时间为5 min,襟翼角为35° 时进行的,得到的平尾结冰严重程度η=0.4。从仿真曲线可以看出,飞机平尾发生结冰后,法向过载急剧增大,易超出其飞行包线;平尾负迎角(Negative Tailplane Angle of Attack,Negative Tail AOA)也增大,易达到平尾临界负迎角,甚至导致平尾失速的发生,因此确定对平尾结冰飞行风险影响最大的两个参数为平尾负迎角和法向过载。提取本次仿真中的平尾负迎角极值αtailmax=8.307 0°,法向过载极值nzmax=1.410 1。 图4 第56次迭代的飞行参数Fig.4 Flight parameters in the 56th iteration 2.2 极值参数可信度验证 图5为i≤100所提取的极值样本与地面试验数据驾驶员在回路地面飞行实时仿真试验数据的散点图和QQ图(若呈一条直线,则两极值样本分布近似相同)。从QQ图可以看出平尾负迎角和法向过载的两种极值样本分位数曲线接近为直线,从散点图可以看出两种极值样本的数据点分布趋于一致,表明所提取的仿真数据和驾驶员试验数据的分布类型近似相同。表1为相关性系数和K-S检验计算结果。K-S值均小于0.1,P值大于0.05,即在95%的置信水平下能通过检验;相关性系数均大于0.9,表明平尾负迎角和法向过载的两种极值样本有强线性相关性。因此,认为所提取的仿真数据和驾驶员试验数据属于同一种分布类型,具有较高的准确性和可信度,可以当作平尾结冰风险评估的样本数据。 图5 提取极值样本与地面试验数据的QQ图和散点图Fig.5 QQ and scatter plots of simulated and ground test extreme value samples 表1 极值样本拟合优度检验Table 1 Goodness-of-fit test of extreme value samples ExtremevaluesampleCorrelationcoefficientK⁃SvaluePαtailmax0.90870.07000.9610nzmax0.95720.08000.8938 2.3 平尾结冰飞行风险判据 (13) 表2为参数极值的统计特性,可以看出峰度系数均大于3,表明所提取的极值样本较集中,比正态分布有更长的尾部;偏度系数均大于0,表明分布类型在右侧具有较长的尾部。因此,可以得出结论:选取的极值参数分布具有较明显的厚尾特性。而极值理论适合对具有厚尾特性的低频高危飞行风险案例进行研究,因此针对此种分布类型,本文采用极值理论对其进行描述。与一维极值分布不同的是,对于二维参数极值分布,需要研究参数之间的相关性,采用Copula理论[22-24]对涉及到多维极值参数的平尾结冰飞行风险概率进行评估具有较高准确性。由Copula理论多元极值分布定义[25]可知:F是多元极值分布函数,则F的一维边缘分布属于GEV(Generalized Extreme Value)分布族。因此,研究参数之间的相关性之前,要先验证一维极值参数符合GEV分布。 表2 极值样本统计量Table 2 Statistics of extreme value samples 3.1 一维极值参数辨识 极值理论中较为广泛应用的有GEV分布(式(14))、正态(Normal)分布(式(15))、对数正态(Lognormal)分布(式(16))、威布(Weibull)分布(式(17))、指数(Exponential)分布(式(18))和EV(Extreme Value)分布(式(19))。分布函数为 (14) (15) (16) (17) F(x;μ)=1-exp-x/μ (18) (19) 式中:ξ、μ、σ均为分布参数。 基于所提取飞行参数极值对以上函数中的未知参数进行辨识,结果如表3所示。 表3不同分布模型的参数辨识 Table3Identifiedparametersofdifferentdistributionmodel ModelExtremeparameterαtailmaxnzmaxGEVξ=0.5020,μ=1.3764,σ=0.0539ξ=0.4690,μ=7.1652,σ=0.2542Normalμ=1.4472,σ=0.1368μ=7.4546,σ=0.5007Lognormalμ=0.3656,σ=0.0882μ=2.0067,σ=0.0649Weibulla=1.5147,b=9.1173a=7.7047,b=13.4147Exponentialμ=1.4472μ=7.4546EVμ=1.5247,σ=0.1732μ=7.7276,σ=0.5878 3.2 拟合优度检验 采用K-S检验法、A-D检验法和卡方检验法对极值参数进行拟合优度检验,来判断飞行极值参数分布函数的准确性。表4和表5为拟合优度检验结果。在平尾负迎角和法向过载的极值参数分布中,GEV分布的K-S检验值小于0.1,P值大于0.05,表明在95%的置信水平下能通过检验。GEV分布的A-D检验值和χ2值相对其他分布非常小,A-D检验的P值远大于0.05,体现出了较高的拟合性。因此,对比GEV和其他分布可以得出,GEV分布的辨识精度远远高于其他分布。 表4 极值参数αtailmax的拟合优度检验Table 4 Goodness-of-fit test of extreme parameter αtailmax 表5 极值参数nzmax的拟合优度检验Table 5 Goodness-of-fit test of extreme parameter nzmax 3.3 极值参数的概率密度图和累计分布图 图6和图7分别为平尾负迎角和法向过载极值参数的概率密度图和累计分布图。由图6和图7 可知,GEV分布对平尾负迎角和法向过载极值样本的描述最为准确,其他分布类型不能如实反映极值样本特征,存在较大误差。 图6 平尾负迎角极值的概率密度图和累计分布图Fig.6 Probability density and cumulative probability maps of extreme negative tail AOA 图7 法向过载极值的概率密度图和累计分布图Fig.7 Probability density and cumulative probability maps of extreme normal overload 综上所述,平尾结冰条件下一维极值参数(平尾负迎角和法向过载)的分布符合GEV分布。 3.4 一维极值参数飞行风险概率计算 根据平尾结冰飞行风险发生的判定条件,将辨识得到的GEV未知参数ξ、μ、σ代入GEV分布式(14),分别以平尾负迎角和法向过载作为风险评估因子,利用式(20)和式(21)求得风险概率分别为0.011 6和0.021 7,根据MIL-STD-882D标准可知,事故发生概率都达到了B水平,即“可能的”。表明平尾结冰对飞机安全性危害极大。 (20) (21) 相同条件下独立求解平尾负迎角和法向过载的风险概率是不同的,说明仅仅考虑某个极值参数评估飞行风险具有一定局限性,因此需要综合考虑多个飞行极值参数。 考虑到极值参数之间的相关性问题,就需要研究边缘分布之间的相关性,建立相关性核函数,本文利用的Copula模型就是采用相同的思路,但广义的Copula模型无法准确描述平尾结冰条件下极值参数之间的相关性,因此,选取适合平尾结冰条件下极值参数相关性的Copula函数是本节的重点。 设随机向量的(αtailmax,nzmax)的分布函数为F(αtailmax,nzmax),边缘分布函数分别为服从GEV分布的u=F1(αtailmax)、v=F2(nzmax)。则对于任意的(αtailmax,nzmax)∈R,一定存在一个CopulaC,使得 C(u,v)=C(F1(αtailmax),F2(nzmax))= F(αtailmax,nzmax) (22) 4.1 二维极值参数辨识 常见的对厚尾特性较敏感的二维阿基米德Copula模型有Gumbel Copula模型(式(23)),Clayton Copula模型(式(24)),GS Copula模型(式(25)),Frank Copula模型(式(26))和Joe Copula模型(式(27))。Gumbel Copula模型、GS Copula模型和Joe Copula模型对飞行参数在分布上尾处的变化较为敏感,能较好地描述上尾相关性;Frank Copula模型对变量之间有近似对称的上下尾部相关结构有较好的描述;Clayton Copula模型对飞行参数在分布下尾处的变化十分敏感,能较好地描述下尾相关性。本文根据二维极值参数的分布规律选取了Joe Copula 模型。 C(u,v)=exp-[(-lnu)β+(-lnv)β]1/θ (23) C(u,v)=(u-β+v-β-1)-1/β (24) (25) (26) C(u,v)=1-[(1-u)β+(1-v)β- (27) 式中:β为不同模型参数。 基于符合GEV的飞行极值参数对以上Copula模型中的未知参数进行辨识,结果如表6所示。 表6 不同Copula模型的参数辨识Table 6 Identified parameters of different Copula models 4.2 拟合优度检验 从表7可以看出,5种Copula模型K-S检验的P值均大于0.05,表明在95%的置信水平下,均能通过检验。其中,Joe Copula模型的AIC(最小信息准则)、BIC值(贝叶斯信息规则,与AIC准则一样,数值越小,拟合精度越高)、χ2值和K-S 值最小,P值最大。因此,相对于其他Copula模型,Joe Copula模型对二维极值分布的描述精度最高。 表7 不同Copula模型的拟合优度检验Table 7 Goodness-of-fit test for different Copula models 4.3 Copula模型的概率密度图 根据表6中未知参数的辨识结果,画出5种Copula模型的概率密度图,如图8所示。图中X、Y轴分别是以平尾迎角和法向过载为极值参数的一维极值分布函数F1(αtailmax)和F2(nzmax),Z轴是所求的二维极值飞行风险概率密度。从图8可以看出,和其他Copula模型相比,Joe Copula模型对厚尾特性描述最好,因此选取Joe Copula模型作为二维极值分布的描述模型。 4.4 二维极值参数飞行风险概率计算 依据Joe Copula模型及平尾结冰飞行风险发生的判定条件求出相应风险概率为 (28) 图8 不同Copula模型的概率密度图Fig.8 Probability density maps of different Copula models 将辨识出的未知参数代入Joe Copula模型,计算得到遭遇平尾结冰为5 min的飞行风险概率为0.026 5(随着设定的遭遇结冰时间的增长,其值增大)。可以看出,综合考虑二维极值参数计算出的平尾结冰飞行风险概率值不是简单地由单个极值算出的风险概率值相加,它比两者都大,但比两者之和小,具有更高的准确性和可信度。 1) 确定对平尾结冰飞行风险影响最大的两个参数为平尾负迎角和法向过载,采用蒙特卡罗法提取出相应飞行极值参数,验证了所提取参数极值符合一维广义极值分布,并建立了平尾结冰飞行风险判断条件,计算出一维极值飞行风险概率。 2) 对多种Copula模型进行参数辨识和拟合优度检验,验证了Joe Copula模型对二维极值分布的描述准确度最高。依据Joe Copula模型及平尾结冰飞行风险判定条件计算出二维极值平尾结冰飞行风险概率,其值比一维极值飞行风险概率大,具有更高的可信度与准确性。 3) 所提出的平尾结冰飞行风险概率评估方法量化地描述了平尾结冰对飞行风险的影响。对飞机平尾结冰情形下的风险规避、控制等问题具有一定的参考价值,是现有飞行适航性准则及飞行安全规范在风险评估方面的有效补充。 4) 由于飞行事故的发生受内外部多方面因素影响,是一个随机的不确定过程,不可能全面准确地考虑到所有因素,因此本文和SAE-ARP-4761、MIL-STD-882E中的飞行风险量化概率在某种程度上都是一个参考值,和真实值存在一定误差。但在平尾结冰飞行风险预测、不同结冰情况下飞行风险的横向对比分析和飞行事故发生概率的等级划分等方面具有积极的意义。 [1] RANAUDO R J, BATTERSON J G, REEHORST A L, et al. Determination of longitudinal aerodynamic derivatives using flight data from an icing research aircraft: AIAA-1989-0754[R]. Reston: AIAA,1989. [2] RATVASKY T P, VAN ZANTE J F. NASA/FAA tailplane icing program: flight test report: NASA/TP-2000-209908[R]. Washington, D.C.: NASA, 2000. [3] BRAGG M B. Aircraft aerodynamic effects due to large droplet ice accretions: AIAA-1996-0932[R]. Reston: AIAA, 1996. [4] GINGRAS D R, DICKES E G, RATVASKY T P. Modeling of in-flight icing effects for pilot training: AIAA-2002-4605[R]. Reston: AIAA, 2002. [5] HAMMOND D, QUERO M, IVEY P, et al. Analysis and experimental aspects of the impact of supercooled water droplets into thin water films: AIAA-2005-0077[R]. Reston: AIAA, 2005. [6] BRAGG M B, HUTCHISON T, MERRET J, et al. Effect of ice accretion on aircraft flight dynamics: AIAA-2000-0360[R]. Reston: AIAA, 2000. [7] AMANDA L, JOHN V. Prediction of icing effects on the coupled dynamic response of light airplanes[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(3): 656-673. [8] ANSELL P J, KERHO M F. Envelope protection for contaminant-induced adverse aerodynamics on a wing using flap hinge moment measurements: AIAA-2013-2654[R]. Reston: AIAA, 2013. [9] THOMAS P R. Demonstration of an ice contamination effects flight training device: AIAA-2006-0677[R]. Reston: AIAA, 2006. [10] THOMAS P R, BILLY P B, LEE S. Current methods modeling and simulating icing effects on aircraft performance, stability, control[J]. Journal of Aircraft, 2010, 47(1): 201-211. [11] 徐忠达, 苏媛, 曹义华.平尾结冰对飞机纵向气动参数的影响[J].航空学报, 2013,34(7): 1563-1570. XU Z D, SU Y, CAO Y H. Effects of tailplane icing on aircraft longitudinal aerodynamic parameters[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1563-1570 (in Chinese). [12] 史刚, 李云. Y-8飞机平尾积冰导致的飞行事故分析[J]. 飞行力学, 2011, 29(5): 84-86. SHI G, LI Y. Study of flight accidents in a row caused by horizontal tail icing[J]. Flight Dynamics, 2011, 29(5): 84-86 (in Chinese). [13] 潘环, 艾剑良. 飞机结冰冰形预测的建模与仿真[J]. 系统仿真学报, 2014, 26(1): 221-224. PAN H, AI J L. Modeling and simulation of aircraft ice shape prediction[J]. Journal of System Simulation, 2014, 26(1): 221-224 (in Chinese). [14] 周莉, 徐浩军, 杨哲. 飞机在结冰条件下的最优边界保护方法[J]. 上海交通大学学报, 2013, 47(8): 1217-1221. ZHOU L, XU H J, YANG Z. Optimal boundary protection method for aircraft under icing conditions[J]. Journal of Shanghai Jiao Tong University, 2013, 47(8): 1217-1221 (in Chinese). [15] 陈斌, 王立文. 飞机除冰液地面除冰过程模型仿真与实验[J]. 系统仿真学报, 2012, 24(3): 556-560. CHEN B, WANG L W. Model simulation and experiment of aircraft deicing process using deicing fluids on ground[J]. Journal of System Simulation, 2012, 24(3): 556-560 (in Chinese). [16] GJB900-90. General program for system safety[S]. 1990. [17] ASE. Guidelines and methods for conducting the safety assessment process on civil airborne systems and equipment: SAE ARP 4761[S]. New York: SAE, 1996. [18] DOD. Airworthiness certification criteria: MIL-HDBK-516B[S]. Washington, D.C.: DOD, 2005. [19] DOD. Standard practice for system safety: MIL-STD-882D[S]. Washington, D.C.: DOD, 2000. [20] STUART C. An introduction to statistical modeling of extreme value[M]. London: Springer, 2007. [21] LAMPTON A, VALASEK J. Prediction of icing effects on the lateral/directional stability and control of light airplanes[J]. Aerospace Science and Technology, 2012: 305-311. [22] STELIOS D B, DIMITRIS A G. Estimation of value-at-risk by extreme value and conventional methods: A comparative evaluation of their predictive performance[J]. Journal of International Financial Markets, Institutions & Money, 2006, 8: 209-228. [23] JOE H. Asymptotic efficiency of the two-stage estimation method for Copula-based models[J]. Journal of Multivariate Analysis, 2005, 94(2): 401-419. [24] FREY R,MENEIL A J. Copula and credit models[J]. The Risk Metrics, 2001. [25] NELSEN R B. An introduction to copulas[M]. New York: Springer, 1999. 王健名男, 硕士研究生。主要研究方向: 飞行器飞行品质与综合控制。 E-mail: 1454893168@qq.com 徐浩军男, 教授, 博士生导师。主要研究方向: 飞行安全与作战效能。 Tel.: 029-84787637 E-mail: xuhaojun@xjtu.edu.cn URL:www.cnki.net/kcms/detail/11.1929.V.20160114.0930.002.html Flightriskevaluationoftailplaneicingbasedonextremevaluetheory WANGJianming,XUHaojun*,XUEYuan,WANGXiaolong,LIZhe AeronauticsandAstronauticsEngineeringCollege,AirForceEngineeringUniversity,Xi’an710038,China AnewmethodcombiningextremevaluetheoryandCopulamodelsisproposedtoquantitativelyevaluatetheflightriskoftailplaneicing.Byestablishingthecomplexpilot-aircraft-environmentmodel,thesituationoftailplaneicingduringapproachingandlandingissimulated.Theflightextremeparameterswhichareprovedtofitthegeneralizedextremevalue(GEV)distributionareextractedthroughMonteCarlomethod.Accordingtothedefinitionofflightriskandrelevantsafetycriterions,theflightriskdeterminationconditionisbuilttocomputetheflightriskprobabilityofone-dimensionalextreme.Thencopulamodelsarechosetodescribethecorrelationoftwo-dimensionalextremeparameters,andunknownparametersindifferentCopulamodelsareidentified.Theresultsofgoodness-of-fittestshowthatJoeCopulamodelhasthehighestaccuracywhendescribingthedistributionoftwo-dimensionalextremeparameters.Thus,theflightriskprobabilityoftwo-dimensionalextremeparametersiscalculatedusingJoeCopula,whichsolvesthelimitationofone-dimensionalextremeparameter.Theapproachhascertainreferencevaluesforthetheoriesofflightsafetyassessment,andprovidesanalysisandteststandardforpreventingflightaccidentinthecircumstanceoftailplaneicing. extremevaluetheory;Copulamodel;tailplaneicing;flightriskprobability;MonteCarlomethod;parameteridentification 2015-12-04;Revised2015-12-30;Accepted2016-01-07;Publishedonline2016-01-140930 s:NationalNaturalScienceFoundationofChina(61374145,61503406);NationalBasicResearchProgramofChina(2015CB755802) .Tel.:029-84787637E-mailxuhaojun@xjtu.edu.cn 2015-12-04;退修日期2015-12-30;录用日期2016-01-07; < class="emphasis_bold">网络出版时间 时间:2016-01-140930 www.cnki.net/kcms/detail/11.1929.V.20160114.0930.002.html 国家自然科学基金 (61374145,61503406); 国家“973”计划 (2015CB755802) .Tel.:029-84787637E-mailxuhaojun@xjtu.edu.cn 王健名, 徐浩军, 薛源, 等. 基于极值理论的平尾结冰飞行风险评估J. 航空学报,2016,37(10):3011-3022.WANGJM,XUHJ,XUEY,etal.FlightriskevaluationoftailplaneicingbasedonextremevaluetheoryJ.ActaAeronauticaetAstronauticaSinica,2016,37(10):3011-3022. http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn 10.7527/S1000-6893.2016.0011 V212 A 1000-6893(2016)10-3011-12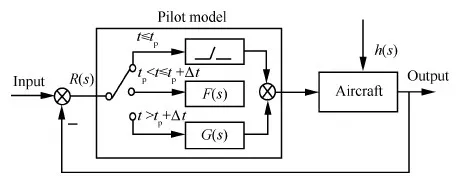

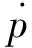


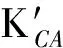

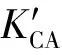
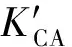
2 基于蒙特卡罗法仿真的二维极值参数选取

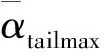
3 一维极值参数分布

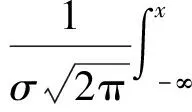

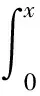
4 二维极值Copula模型


5 结 论

