“铺垫·创境·争论·反思”
周梅琦

[摘 要] 初中学生数学探究能力的培养要注重“铺垫·创境·争论·反思”活动的展开,注重数学知识的梳理和数学思路的引导,注重学生的探究体验.
[关键词] 探究;铺垫;创境;争论;反思
数学素养构成中,最为重要的成分便是探究能力,因为它是自主性学习的深化,是创新能力形成的必经路径. 探究能力的高低直接决定学生数学素质的高低,表现为能否在日益注重素养考查的考试中考取高分. 毫无疑问,探究能力与学生的智商有着密不可分的关系,但是,同样的智商条件,学生的探究能力会产生差异,这很大程度上取决于探究能力的培养. 为此,笔者认为,应当关注探究过程,努力构建探索能力的形成机制.
铺垫
“铺垫”即事物发展过程中的前期准备工作,是数学探究能力形成的基础性准备和前提条件. 数学探究问题一般具有一定的复杂性,往往关键的条件,哪怕是一个数据、一个小数点、一条线段、一个未知数等,都可能影响整个探究活动的成败,而这些条件所牵涉到的知识或技能往往又是基础性的、前置性的,是在探究活动展开之前就应该掌握的. 一般而言,探究问题具有极强的综合性,往往将简单的单项知识或技能整合起来,构成一个复杂的系统,而抽出若干条件,让学生探究. 所以,分析探究问题所牵涉的知识和技能的铺垫,从中打开探究问题的突破口,是数学探究能力形成的重要路径.
比如,下面的题目:如图1,已知抛物线的顶点为A(0,1),矩形CDEF的顶点C,F在抛物线上,D,E在x轴上,CF交y轴于点B(0,2),矩形CDEF的面积为8.
(1)求此抛物线的解析式;
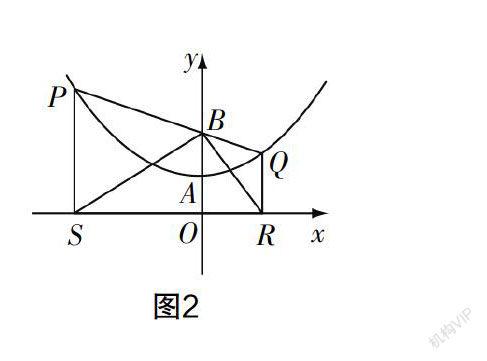
(2)如图2,若点P为抛物线上不同于点A的一点,连接PB并延长交抛物线于点Q,过点P,Q分别作x轴的垂线,垂足分别为S,R.①求证:PB=PS;②判断△SBR的形状;③试探索在线段SR上是否存在点M,使得以点P,S,M为顶点的三角形与△BOR相似,若存在,请找出M点的位置;若不存在,请说明理由.
像这样的问题,几乎囊括了初中数学重要的知识点,诸如一元一次方程、平面直角坐标系、一次函数与二次函数解析式的求法(图像及其性质)、四边形(特殊)的性质、直角三角形的性质、解直角三角形、相似三角形等,而对于用几何图形的某些特殊性质,如勾股定理、相似三角形对应线段成比例等来构造方程,更是被广泛应用. 如果没有这些铺垫,探究问题就无法进行下去.
创境
“创境”即创设探究问题的情境,一是探究的氛围,针对重难点问题,提出引而不发的问题,积极鼓励学生展开探究;二是设置具体的问题情境,让知识和技能在实际的生产应用、生活情境当中鲜活起来. 通过人为创设障碍,提高探究问题的挑战性,吸引学生深入研究、思考,提高分析问题、解决问题的能力.
课堂教学中教学点必然会遭遇理解瓶颈,课堂活动的重点也必将因之产生,难点也会自然呈现. 教师如果在重难点上没有充分发力,引导学生展开探究,那就不可能完成教学任务,达到预期的教学目标.
比如苏科版八年级下册第9章“中心对称图形——平行四边形”第一节“图形的旋转”,其教学重难点是“一个图形和它经过旋转所得到的图形中,对应点到旋转中心的距离相等,两组对应点分别与旋转中心连线所成的角相等”. 教材先从实例阐述,逐步引导出这个结论. 但是,这必须用数学思维去验证,而抽象的想象不可能将这一结论深深地嵌入学生的知识结构之中,那么,我们就应该设置探究问题,鼓励学生独立探索,主动建构. 教学伊始,笔者便将这个结论直接摆出来,问学生:
“大家觉得这句话可信吗?”(得到不同的回答,不少学生半信半疑)
“这没关系,科学来不得一点儿虚假,我们必须用科学的思维去求得科学的结论. 所以,接下来,同学们从数学的角度,用数形转化的方式,来破解这一谜题吧!”
“不过,请答应我一个条件——不要再看教材,自己或者寻求小组合作探究,看看这其中的神奇世界. ”
设置这个条件,其实就是为了避免教材现成的素材对学生的探究活动产生消极的、先入为主的干扰,以求得探究效果的最大化.
通过课堂观察,笔者获悉,学生分别采用了数轴、实物等方式方法,建构旋转的概念;也采用了几何图形画图的形式,尝试不同图形的旋转效果. 最后笔者引导学生充分阅读教材中的阐述和示例,彼此分享探索体验. 在此基础上,笔者又设计了一组实际运用的情境. 反馈表明,这样的探究指导使学生获得了理想的学习效果,学生的探究能力得到进一步提升. 可见,“探究式情境的设置对教师及学生的帮助是非常大的,它要求教师在学生学习新的数学知识前,要设置一定的疑问作为铺垫. ”
争论
“争论”即针对探究过程中产生的不同认知和结论,进行辩论. 争论的实质是学生数学思维的碰撞、数学认知的交锋,是深层的分享和交流. 没有争论也就没有了探究,探究必然要生成质疑,质疑则促进探究. 课堂活动中,学生动用足够的数学知识支撑自己的数学发现和观点,就会对他人产生积极的影响,也能在争论中更加清楚地认知自身的发现的科学性,从而有利于自我的建构,在顺应和同化中登临更美的数学风景.
比如苏科版九年级上册“一元二次方程”中有这样的描述:“任何一个关于x的一元二次方程都可以化成ax2+bx+c=0(a,b,c是常数,a≠0)的一般形式. ”针对这个描述,为了加深学生的印象,我们可以这样设问:为什么规定“a≠0”这个限制条件呢?b可以为0吗?对于第一个问题,学生根据方程的概念即可准确判断,但对于第二个问题则产生了争论.
生1:不能为0,因为如果为0就不叫一元二次方程的一般形式了.
生2:可以为0,“ax2+c=0”这样的形式也应该叫一元二次方程,它符合一元二次方程的概念特点.
生3:c可以为0. 比如“ax2+bx=0”,根据概念,它也应该是一元二次方程.
生4:b,c可以同时为0. “ax2=0”也是一元二次方程,只不过它的解是唯一的,只能为0.
师:看来,判断一个方程是不是一元二次方程的关键有两个:一是未知数的最高次数必须为2;二是未知数的二次项系数不能为0.
通过争论,学生对一元二次方程的概念及表现形式有了更为透彻的理解,遇到类似的探究问题也就不会忽略一元二次方程的构建条件了. 可见,争论的过程本身就是一个美妙的生成,生动地创造着数学探究活动的情境. 其实,在各种各样的探究活动中,一个方案的设计,一种思路方法的选择,一个辅助线的加设,一个解题步骤的布局等,都可以引起争论. 在争论中,教学活动才会使明者更明,误者纠误,水落石出.
反思
探究活动具有极强的生成性,也会给学生带来诸多的意外,既有可能寻找到最佳路径,也有可能产生迷茫,往往形成“山重水复疑无路,柳暗花明又一村”的局面. 反思探究的过程便会从中捡拾丢落的贝壳,汲取失败的教训,储备成功的经验. 引导学生养成反思的习惯,就能生成数学智慧,帮助他们挑战更大的数学探究问题. 反思必须产生“惑”,学生有了疑惑才会主动去思考学习,产生对学习的积极性. 教师应主动去判断学生是否产生“惑”,如果判断学生没有产生“惑”,教师应对学生进行诱导,使学生产生“惑”.
比如,苏科版九年级下册第69页“直线与圆的位置关系”之“如何做一个圆,使它与已知三角形的各边都相切”. 学生动手探索之后,笔者便提问:“这里用到了哪些知识?”
生1:圆的切线与圆心的关系.
生2:圆与三角形之间的关系.
生3:圆心与三角形内角和之间的关系.
师:我们使用了什么方法来完成这个探索?
生:利用角平分线求得圆心.
师:遇到问题时,我们应该善于驱动相关的数学知识和技能. 要知道,任何复杂的问题都是由一个个细小的数学概念构成的,如果我们能像庖丁解牛那样,就能破解难题,从复杂的数学关系中理出头绪来.
当然,反思的路径、项目可以有所侧重. 只要有利于总结得失,梳理数学思路,就会促进学生探究能力的不断提升.
总之,培养学生的数学探究能力需要多管齐下,不囿于一招一式. 我们只要善于梳理出相关的数学知识和技能,抓住关键问题,就能够游刃有余地打破探究瓶颈;只要善于引导反思,及时将探究体验升华成数学思想,就能够为学生的数学探究活动营造浓浓的情意场,深度带动学生乐于探究、善于探究.
——宅

