基于平均驻留时间法的网络切换模糊系统非脆弱控制

薛知言，刘 毅

(天津城建大学 计算机与信息工程学院，天津 300384)

信息科学与技术

基于平均驻留时间法的网络切换模糊系统非脆弱控制

薛知言，刘 毅

(天津城建大学 计算机与信息工程学院，天津 300384)

针对带有时滞和参数不确定的非线性网络切换控制系统，采用模糊 T-S模型建模，研究了控制器增益存在摄动情况下系统的指数稳定性．采用平均驻留时间法设计切换律，并设计切换模糊状态反馈控制器，给出了网络切换模糊系统指数稳定的平均驻留时间条件．证明了每个子系统在反馈控制访问率不低于稳定条件的切换策略下可以达到指数稳定．最后通过 MATLAB数值仿真验证了本文方法的有效性．

网络控制；切换模糊系统；平均驻留时间；非脆弱控制

网络控制系统(NCSs)是由控制器、执行器和通信网络组成的闭环控制系统，其核心是系统通过网络通信信道进行反馈控制的控制器和执行器．NCSs可以满足分散化控制要求，系统的控制器和执行器等组成部分能分布在不同地点，仅通过网络环境进行反馈控制[1-6]．这种控制方式将网络通信应用于大型复杂分散化控制系统，可实现资源共享和远程操作，是控制系统发展的一个重要趋势，拥有广阔的前景[7-9]．

对于切换系统，现在普遍采用设计适合切换策略的方法来实现系统稳定控制，因此可利用切换方法，对网络控制系统进行分析[10-12]．另一方面，以平均驻留时间法为典型的切换策略设计，能够找到使系统在满足相应切换条件下达到稳定的有效条件．文献[13]引入了平均年驻留时间方法对线性不确定系统进行稳定控制．但是工程应用中更为常见的系统都是离散化的，对于此类系统，目前的文献研究里还少有涉及．另外在实际中，控制器会存在参数的不可控变化，系统模型中反馈增益将出现ΔK不确定项，这种变化会增加系统的稳定控制难度，使稳定性受到影响，因此考虑控制器摄动具有现实意义[14-15]．

本文应用平均驻留时间方法，对于带有时滞和参数不确定的非线性网络切换控制系统，采用模糊T-S模型建模，利用Lyapunov函数给出了模糊状态反馈控制器，以及使系统指数稳定的平均驻留时间条件，相应结果以矩阵不等式的形式给出．

1 问题描述

整个 NCSs由多个闭环反馈子系统组成切换系统，且开环不稳定，但是在合适的切换策略下，可以使系统达到稳定．数据采用单包形式传输，传感器采用时间驱动，控制器和执行器为事件驱动，且具有多个控制器、执行器通过网络通信方式进行控制[16]，如图1所示．

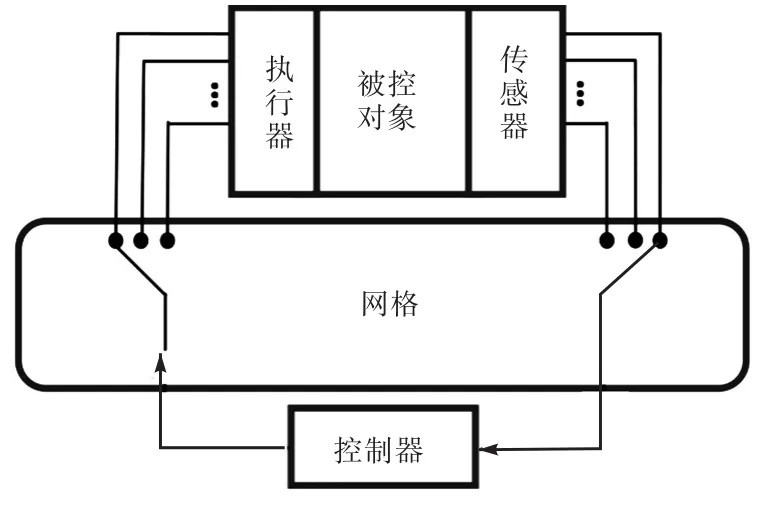
图1 网络控制系统模型

考虑 NCSs会受干扰以及时延的影响，将系统描述如下：第 i条模糊规则表明Z1(k)是，以此类推Zp(k)是，即

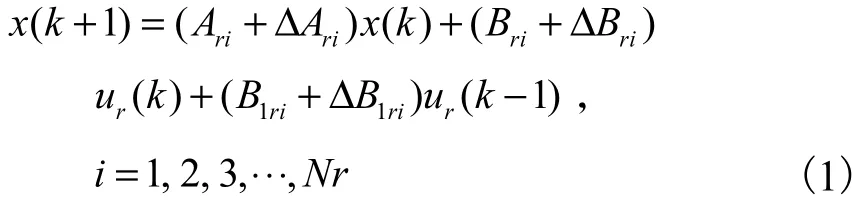
本文考虑矩阵ΔAri、ΔBri以及参数不确定的情况，且满足以下条件

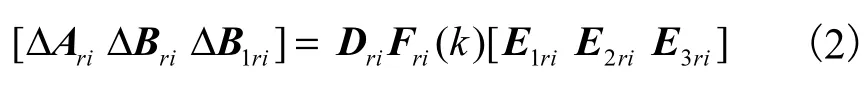
式中：Dri、E1ri、E2ri、E3ri是具有适当维数的已知常数矩阵；Fri(k)是未知时变矩阵，且满足，r∈ M=1,2,…,Nr．

如果 NCSs中单独一个子系统的反馈控制通道保持在状态是闭环的时间足够长，且在开环、闭环之间切换频率满足一定条件的情况下，该系统是能够达到指数稳定的，因此切换信号r=r(x(k))必须满足平均驻留时间的条件．另外用函数vr(x(k))表示切换信号，当子系统得到切换信号时vr(x(k))=1子系统可以通过网络进行闭环反馈控制，反之则vr(x(k))=0．

对式(1)，根据平行分布补偿算法(PDC算法)，由单点模糊化、乘积推理和平均加权反模糊化设计，整个网络切换模糊系统的全局模型为

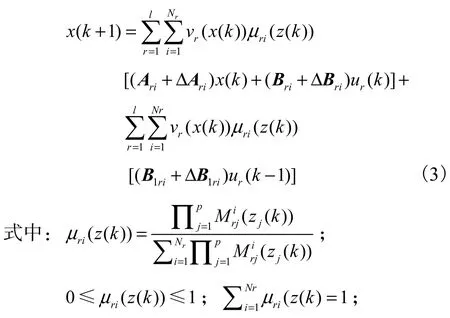
另设计反馈控制器为如下形式

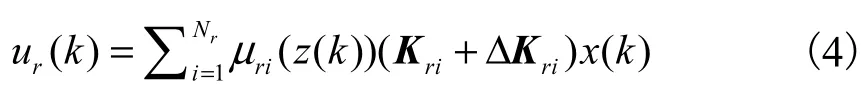
式中：Kri为控制增益矩阵；ΔKri为控制器增益摄动，且满足下式

式中：Hri和Gri是适维常数矩阵；Rri(k)是时变矩阵，为未知项，且满足Rri(k)TRri(k)≤I，r ∈M=1,2,...,Nr．

将式子合并代入后，可得整个系统的模型为

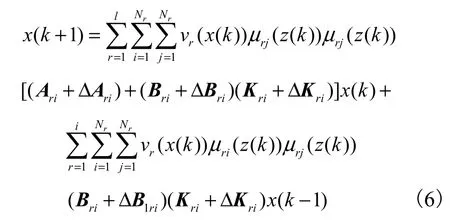
定义 对任意时刻t2＞t1≥0，用Nr(t1, t2)表示时间段[t1, t2]上的切换次数．若存在Tα＞0，No≥0使得不等式，即成立，那么常数Tα就称为平均驻留时间，另外本文取No=0．

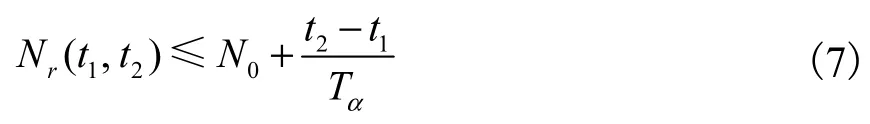
引理[17]有适维矩阵 H、E、I和对称矩阵 Q，对所有满足Fri(k)TFri(k)≤I的矩阵Fri(k)，当存在某个ε≥0，满足Q+ε2HHT+ε-2FTE≤0时，有Q+HFri(k )E+ETFri(k)THT≤0．

2 结果分析

定理1 若存在对称正定矩阵 Pr、Sr，以及常数λ∈(0,1)，使矩阵不等式

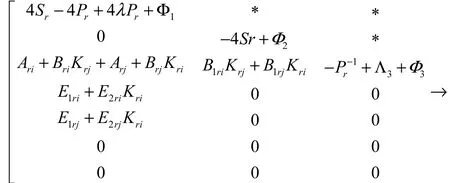
成立，则系统对平均驻留时间满足

条件的切换律，存在反馈控制器(4)，使式(1)指数稳定，且系统的状态估计为

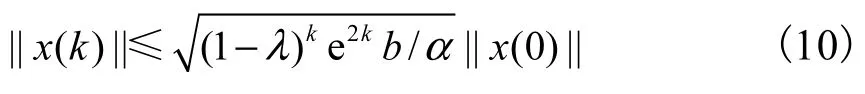
其中：*表示对称位置矩阵的转置；μ 满足V(ki)≤μV(kj)，∀i, j∈M，V(k)为一个正定二次型函数．

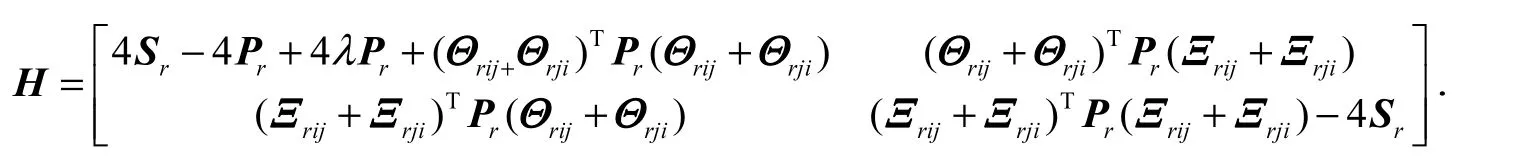
利用Schur引理，H矩阵可变形为

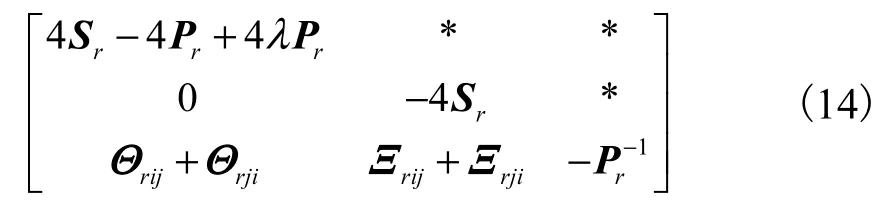
式(14)又等于以下两矩阵之和，以此可从中分离出不确定项，即

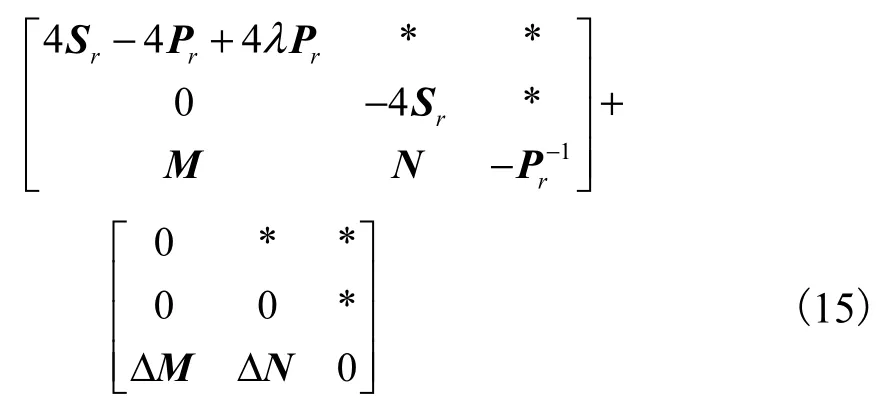
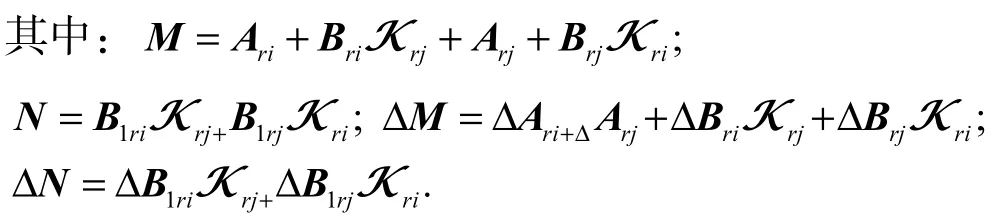
式(15)中的第二项由式(2)和引理可化简消除不确定项，即

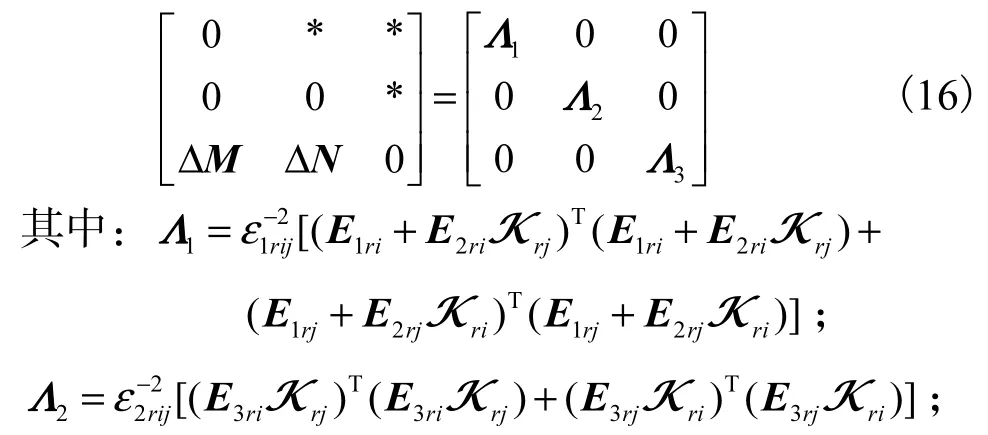
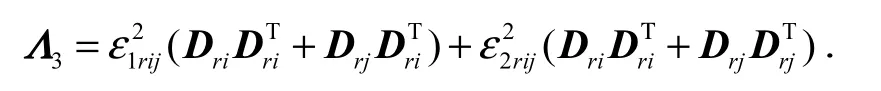
因此，式(14)能够化简成为如下矩阵

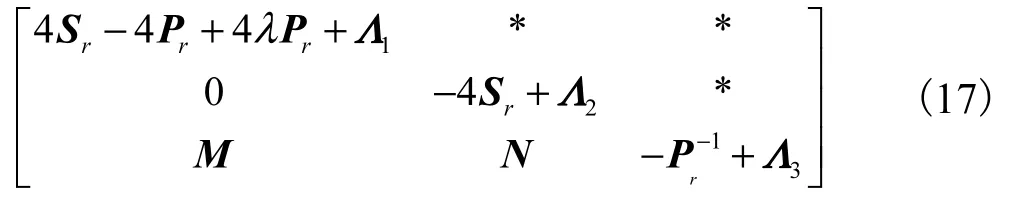
再利用Schur引理，式(17)矩阵又可变为

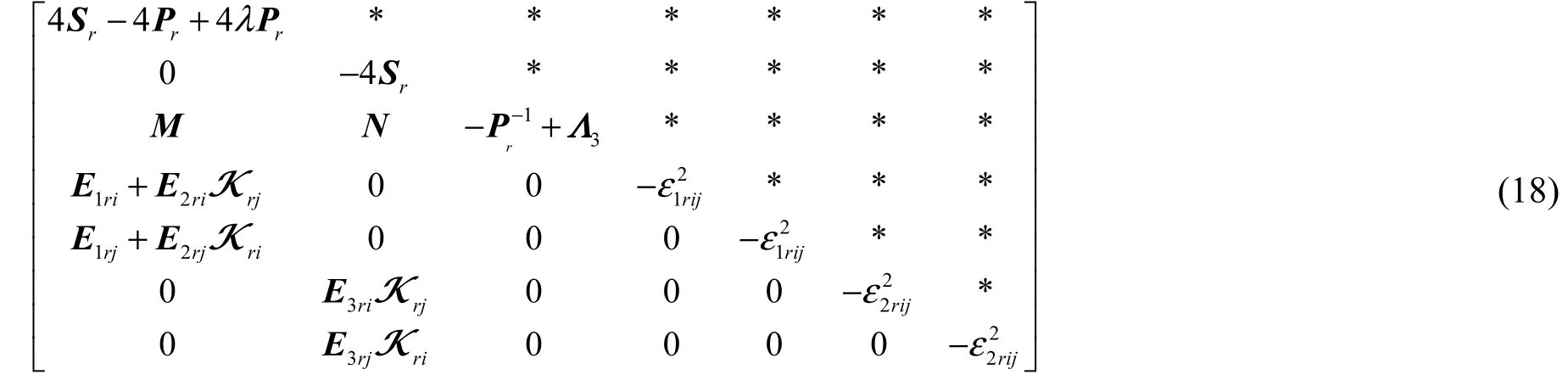
而式(18)又等于两矩阵之和，即

将(19)式中的第二项由(5)和引理再一次化简可得

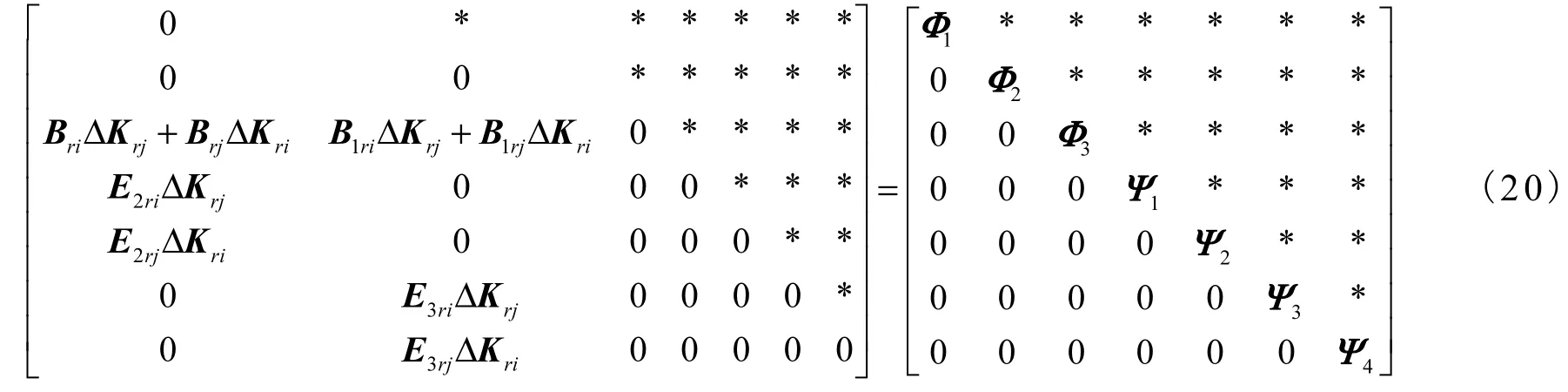
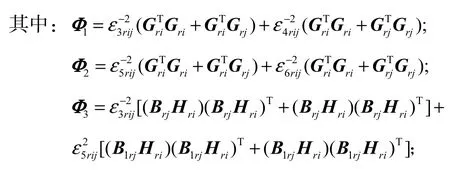
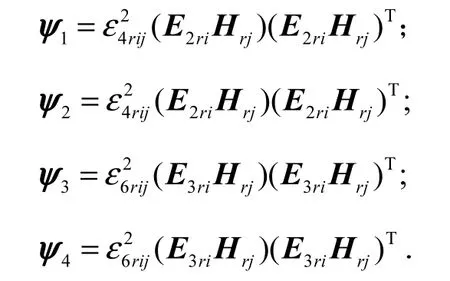
综上，(18)可以最终化简成

以上推导说明：在满足定理中式(8)条件下V(k+1)-V(k)+λV(k)≤0，即

由(10)、(11)及上式(22)可得

进一步推导，由(7)、(9)及式(23)可得

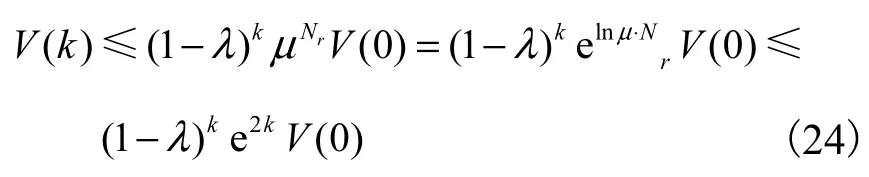
则由(11)和式(24)可得α||x(k)||2≤V(k)，

最终可得指数稳定的状态估计，即

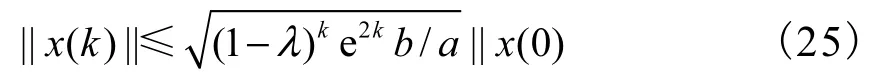
因此，式(1)可以达到指数稳定．

3 仿真例子

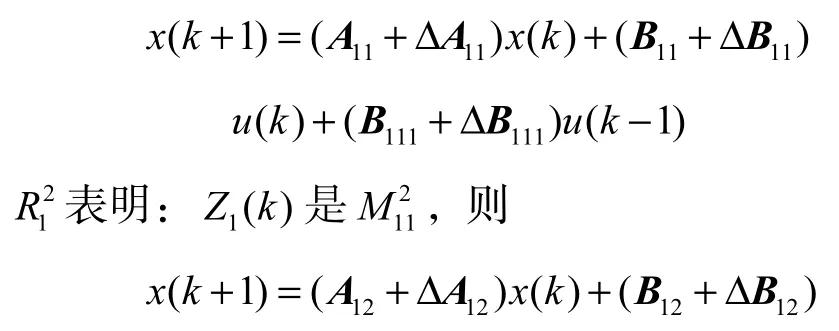
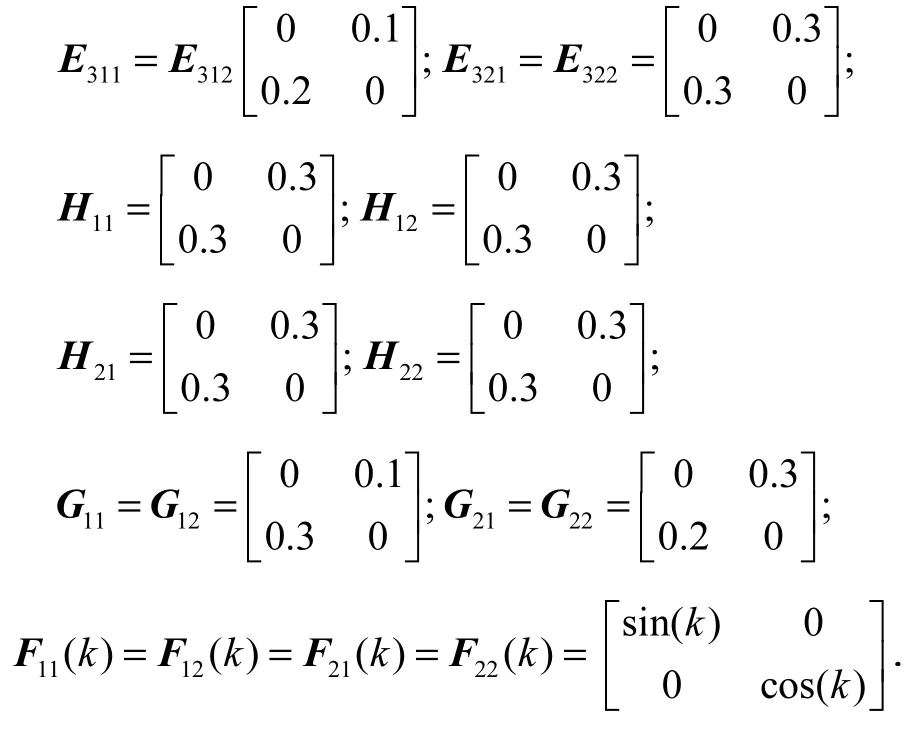
取隶属度函数为

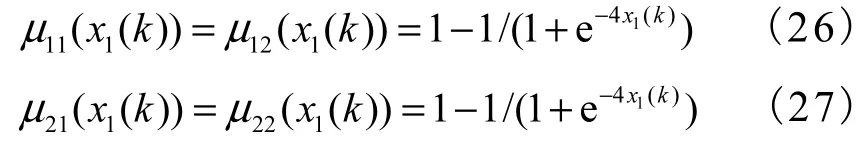
取εrij=1，令λ=0.15，μ=2.225，解矩阵不等式(5)得正定矩阵及反馈增益矩阵解为

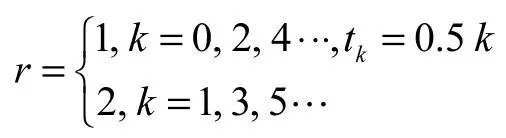
用MATLAB仿真，选取初始点为[-0.1,0.3]T，仿真结果如图2所示．可以看出系统可以快速收敛，因此可得出结论，使用本文方法所设计的系统可以达到指数稳定．

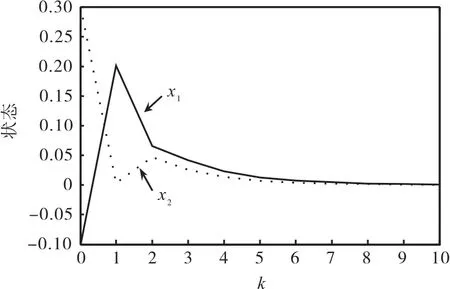
图2 网络切换模糊系统状态曲线

4 结 语

本文针对带有时滞和参数不确定的非线性网络切换控制系统，研究其非脆弱控制问题．基于平均驻留时间法，利用Lyapunov函数设计了模糊状态反馈控制器，以及使系统指数稳定的平均驻留时间条件．结果表明，如果一个反馈控制系统的访问率不小于某个值，则该系统是可以稳定的．

［1］ 游科友，谢立华. 网络控制系统的最新研究综述[J].自动化学报，2013，39(2)：101-118.

［2］ 李洪波，孙增圻，孙富春. 网络控制系统的发展现状及展望[J]. 控制理论与应用，2010，27(2)：238-243.

［3］ XU Yang．Stability analysis of networked control systems with round-robin scheduling and packet dropouts [J]. Journal of the Franklin Institute，2013，350(8)：2013-2027.

［4］ 何 涛，张小美，周儒娟. 基于平均驻留时间方法的网络化系统的模糊控制[J]. 工程数学学报，2013，30(2)：184-196.

［5］ 朱信成，周 川，陈庆伟. 网络控制系统的模型依赖平均驻留时间调度与控制[J]. 控制理论与应用，2015，32(1)：86-92.

［6］ 杜明莉，周 川，陈庆伟. 具有通信约束的网络控制系统动态调度与 H∞ 控制协同设计[J]. 控制理论与应用，2012，29(9)：1132-1138.

［7］ 盖彦荣，陈阳舟，张亚霄，等. 离散时间多智能体系统一致性的平均驻留时间条件[J]. 控制与决策，2014，29(10)：1871-1875.

［8］ 王 茂，樊友高，邱剑彬. 饱和不确定离散切换系统的静态输出反馈控制[J]. 控制与决策，2010，25(10)：1479-1483.

［9］ 杨 红，赵 军，张 乐. 一类离散切换模糊系统的稳定性[J]. 控制理论与应用，2007，24(5)：861-865.

［10］ LIU Yi，ZHAO Jun. Non-fragile control for a class of uncertain switching fuzzy time-delay systems [J]. Journal of Control Theory and Application，2010，8(2)：229-232.

［11］ 朱信成，周 川，陈庆伟. 网络控制系统的模型依赖平均驻留时间调度与控制[J]. 控制理论与应用，2015，32(1)：86-92.

［12］ 谢成祥，胡维礼. 一类具有数据包丢失的长时延网络控制系统的分析与设计[J]. 控制理论与应用，2010，27(9)：1207-1213.

［13］ 汪 锐，冯佳昕，赵 军. 一类线性不确定切换系统的非脆弱控制器设计方法[J]. 控制与决策，2006，21(7)：735-738.

［14］ DONG YUE，LAM J. Non-fragile guaranteed cost control for uncertain descriptor systems with time-varying state and input delays [J]. Optimal Control Applications and Methods，2005，26(2)：85-105.

［15］ XIA Yuanqing，JIA Yingmin. Robust sliding-mode control for uncertain time-delay systems：an LMI approach [J]. IEEE Transactions on Automatic Control，2003，48(16)：1086-1091.

［16］ 刘 毅，冯佳昕，赵 军. 不确定离散切换模糊时滞系统的鲁棒输出反馈控制[J]. 东北大学学报(自然科学版)，2009，30(1)：13-16.

［17］ TONG Shaocheng，TANG Jiantao，Wang Tao. Fuzzy adaptive control for multivariable nonlinear systems[J]. Fuzzy Sets and Systems，2000，111(2)：153-167.

Non-Fragile Control for Network Switched Fuzzy System Based on Average Dwell Time Method

XUE Zhiyan，LIU Yi
(School of Computer and Information Engineering；TCU，Tianjin 300384，China)

Switching laws based on average dwell time method and switched fuzzy non-fragile state feedback controller are designed for a network switched fuzzy control system．The controller to be designed is assumed to have additive gain variations．Sufficient condition for exponentially stability is also presented in our study．Finally，a simulation example shows the effectiveness of the proposed approaches mentioned in the study as well.

networked control；switched fuzzy systems；average dwell time；non-fragile control

TP273

A

2095-719X(2016)05-0380-07

2015-05-11；

2015-06-10

薛知言（1990—），男，江苏苏州人，天津城建大学硕士生.