拟齐次平面多项式系统的逆积分因子

韩美佳，黄土森

(浙江理工大学理学院，杭州 310018)



拟齐次平面多项式系统的逆积分因子

韩美佳，黄土森

(浙江理工大学理学院，杭州 310018)

逆积分因子是研究平面多项式系统可积性问题的重要工具。对于拟齐次多项式系统，利用广义Euler定理证明了它一定存在多项式逆积分因子，并给出了具体表达式；对于由两个拟齐次多项式系统的和所定义的多项式系统，给出存在多项式逆积分因子的一个充分条件，并由此给出几类特殊多项式系统的逆积分因子的计算公式。给出的几个多项式逆积分因子计算例子表明这些结论推广了已有成果。

拟齐次多项式系统；多项式逆积分因子；拟齐次分解

0 引 言

平面自治微分系统可表示为：

(1)

其中P和Q是一个从R2的一个开集U到R的Cr映射，r≥1。令W是U的一个开子集。对于一个可微的非常值函数V：

V:W→R.

如果它满足一阶线性偏微分方程：

则称V(x,y)为系统(1)的在W上的一个逆积分因子[1]。进一步，如果W=R2，且V:R2→R还是一个多项式，则称V(x,y)为系统(1)的多项式逆积分因子。

系统(1)的逆积分因子具有以下一些重要性质：

a)V-1(0)={(x,y)∈W|V(x,y)=0}由系统(1)的轨线组成[2-3]。

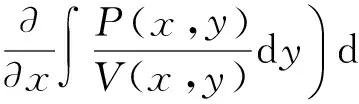
c)若系统(1)在W上存在极限环γ，则γ⊂V-1(0)[4]；进一步，如果Г是位于W中由鞍点与正则轨线组成的多环，则Γ⊂V-1(0)[3]。

系统(1)的这些性质表明：逆积分因子是研究可微平面系统的可积性问题[1, 5]、中心问题[6-7]和平面多项式系统极限环个数与分布问题[2,8]的重要工具之一。一般而言，系统的逆积分因子的表达式比首次积分简单，定义域比首次积分的大[1]。因此，如何求得给定系统(1)的逆积分因子对确定系统性态具有重要作用[9]。

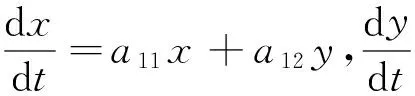
本文首先给出拟齐次多项式系统的多项式逆积分因子的表达式；然后把文献[15]中由两个齐次多项式系统的和所定义的多项式系统推广到拟齐次的情形，给出存在多项式逆积分因子的一个充分条件，并由此给出几类特殊多项式系统的多项式逆积分因子的计算公式；最后给出例子以说明这些推广的实用性。

1 主要结果及其证明

考虑多项式系统：

(3)

(4)

引理1 (广义Euler定理) 设f(x,y)是t型k次的拟齐次多项式，则恒等式(5)成立。

(5)

定理1 对于t型k次的拟齐次多项式系统：

(6)

则它有多项式逆积分因子：

(7)

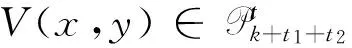
证明 只需验证(7)满足(2)。实际上，因为：

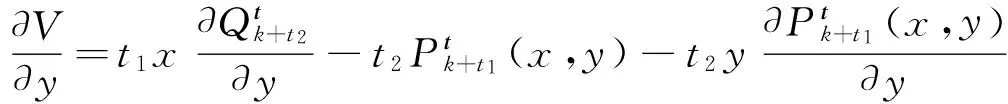
又由引理1知，

所以：

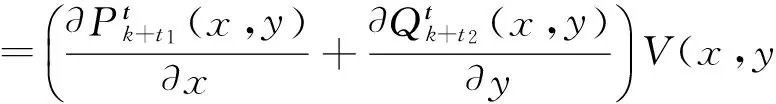
证毕。

文献[12]研究如下形式

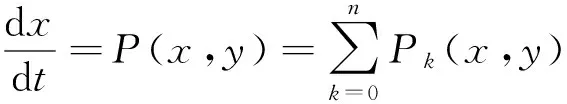
(8)

的多项式系统存在多项式逆积分因子的必要条件，其中Pk(x,y)和Qk(x,y)均为k次齐次多项式，k=0,1,…,n。而文献[15]研究如下形式

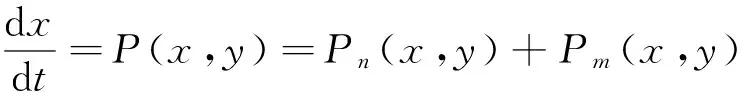
(9)

的多项式系统存在多项式逆积分因子的充分条件，其中Pk(x,y)和Qk(x,y)均为k次齐次多项式，k=n,m。本文把这些结论推广到多项式系统进行拟齐次分解的情形，即对任意给定的t=(t1,t2)，把系统(3)写成系统(4)的形式。因为系统(6)有形如

(10)

的多项式逆积分因子，其中“·”表示内积，因此有理由假设式(4)有形如

(11)

的多项式逆积分因子，其中Ck是待定常数，k=r,…,n。为使系统(11)是系统(4)的多项式逆积分因子，只需把系统(11)代入系统(2)，并让等式两边的同次幂系数相等，得到关于待定常数Ck的代数方程组。一般地，这个代数方程组是超定的，这也表明系统(4)未必有多项式逆积分因子，但由此可以研究系统(4)存在具有形式为系统(11)的多项式逆积分因子的充分条件。现在本文利用这种方法研究形如

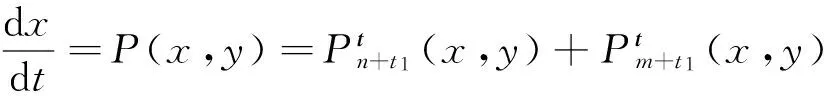
(12)

的多项式系统存在多项式逆积分因子的充分条件，不妨设n≠m。

定理2 对于系统(12)，如果存在实常数Cn≠Cm，满足

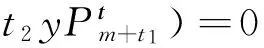
则系统(12)有形如

的多项式逆积分因子。

证明 记

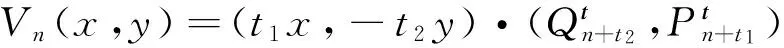
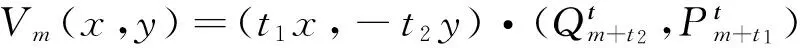
则V(x,y)=CnVn(x,y)+CmVm(x,y)。现只需要证明V(x,y)满足系统(2)。因为：

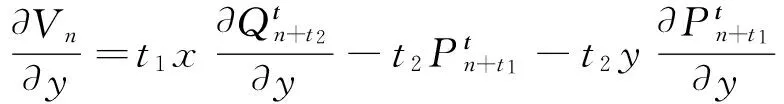
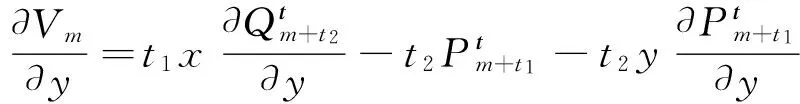
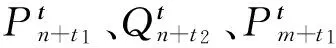
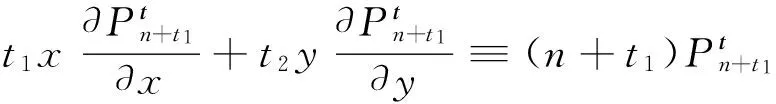
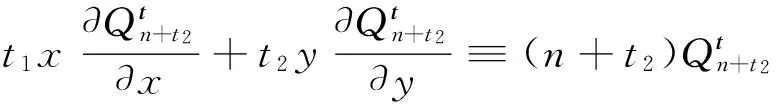
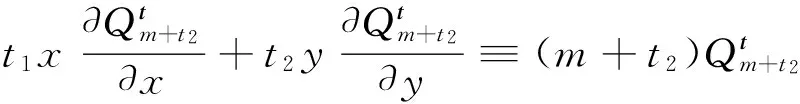
所以：

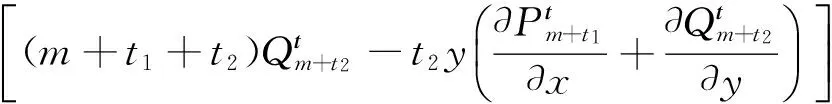
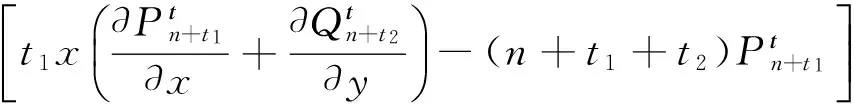
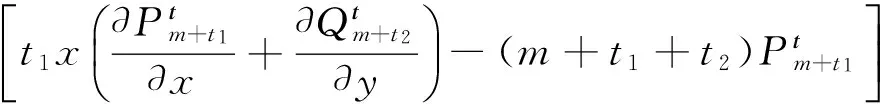
而

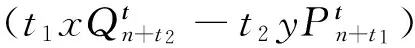
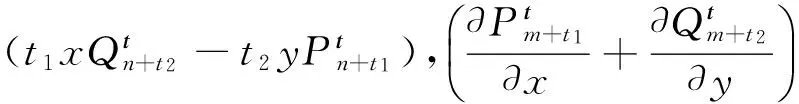
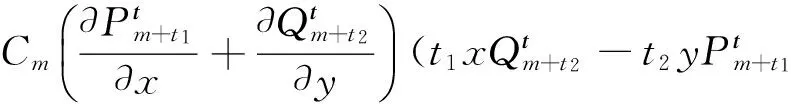
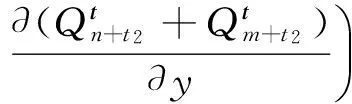
[Cn(n+t1+t2)-Cm(m+t1+t2)]

如果允许Cn=Cm，则为使

是系统(12)的多项式逆积分因子，则由于n≠m，因此

Pm+t1Qn+t2-Pn+t1Qm+t2=0

成立,即系统(12)的右边不是互素的，导致系统(12)的原点不是孤立奇点。

推论1 对于系统(12)，如果

推论2 对于系统

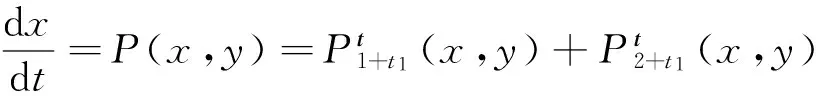
(13)

如果

成立,其中C1≠C2是实常数，则它存在多项式逆积分因子

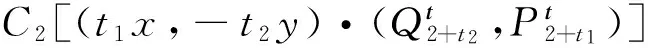
推论3 对于系统(13)，如果成立

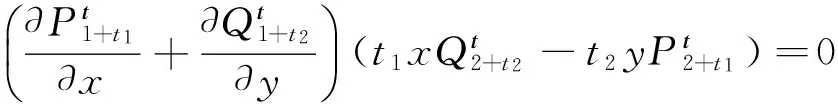
则它存在多项式逆积分因子

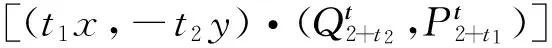
2 例 子

本节给出两个例子说明本文定理的应用，以此说明本文的结果推广了文献[12, 15]中的结论。

例1 考虑系统

(14)

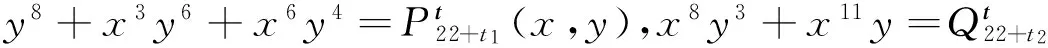
V(x,y)=2x9y3+2x12y-3y9-3x3y7-3x6y5。

例2 取t=(t1,t2)=(2,3)，考虑系统[17]

(15)

其中:

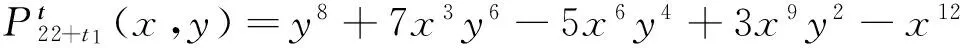
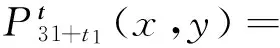
-2x15y，

15x14y2+2x17.

因为

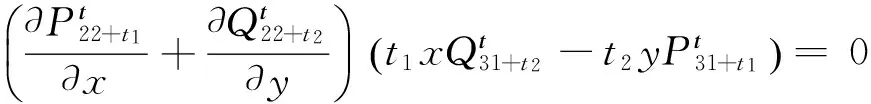
所以由推论1知，系统(15)存在多项式逆积分因子：

V(x,y)=-3y9-27x3y7+27x6y5-27x9y3+

27x12y-27x3y10+27x6y8-27x9y6+

27x12y4-27x15y2-3x18.

注意到，由于系统(14)和(15)都不是齐次系统，也不是形式(9)的系统，因此不能利用文献[12, 15]中的结论求它们的多项式逆积分因子。

3 结 论

由于逆积分因子包含了微分方程系统的一些重要信息，因此它是研究可微平面系统的可积性问题、中心问题和平面多项式系统极限环个数与分布问题等定性理论中经典问题的重要工具之一。对于一个给定的多项式系统，要判断它是否存在逆积分因子，以及如果存在,如何求它的逆积分因子十分困难。而对于一个多项式系统，要判断它是否存在多项式逆积分因子、如果存在如何求出这样的逆积分因子就更困难。本文对于拟齐次多项式系统，证明了总存在多项式逆积分因子并给出了它的具体表达式；进而对于由两个拟齐次多项式系统的和所定义的多项式系统，通过假设逆积分因子的特定形式，给出存在多项式逆积分因子的一个充分条件，并由此给出几类特殊多项式系统的逆积分因子的计算公式；最后通过两个例子计算多项式逆积分因子以说明本文结果推广了已有成果。对存在多项式逆积分因子的多项式系统进行分类有待继续研究。

[1] CHAVARRIGA J, GIACOMINI H, GINE J, et al. On the integrability of two-dimensional flows[J]. Journal of Differential Equations,1999,157(1):163-182.

[2] GIACOMINI H, LLIBREZ J, VIANO M. On the nonexistence, existence and uniqueness of limit cycles[J]. Nonlinearity,1996,9(2):501-516.

[3] BERRONE L R, GIACOMINI H. On the vanishing set of inverse integrating factors[J]. Qualitative Theory of Dynamical Systems,2000,1(2):211-230.

[4] GIACOMINI H, VIANO M. Determination of limit cycles for two-dimensional dynamical systems[J]. Physical Review E,1995,52(1):222-228.

[5] CHAVARRIGA J, GIACOMINI H, GINE J, et al. Darboux integrability and the inverse integrating factor[J]. Journal of Differential Equations,2003,194(1):116-139.

[6] GINE J. The nondegenerate center problem and the inverse integrating factor[J]. Bulletin Des Sciences Mathématimatiques,2006,130(2):152-161.

[7] GINE J. On the centers of planar analytic differential systems[J]. International Journal of Bifurcation and Chaos in Applied Sciences and Engineering,2007,17(9):3061-3070.

[8] GINE J, LLIBRE J. Integrability and algebraic limit cycles for polynomial differential systems with homogeneous nonlinearities[J]. Journal of Differential Equations,2005,197(2):531-545.

[9] GARCIA I A, GRAU M. A survey on the inverse integrating factor[J]. Qualitative Theory of Dynamical Systems,2010,9(1):115-166.

[10] CHAVARRIGA J. Integrable systems in the plane with a center type linear part[J]. Applicationes Mathematicae,1994,22(2):285-309.

[11] CHAVARRIGA J, GINE J. Integrable systems via inverse integrating factor[J]. Extracta Mathematicae,1998,13(1):41-60.

[12] CHAVARRIGA J, GIACOMINI H, GINE J. Polynomial inverse integrating factors[J]. Annals Differential Equations,2000,16(4):320-329.

[13] WALCHER S. Local integrating factors[J]. Journal of Lie Theory,2003,13(1):279-289.

[14] FERRAGUT A. Polynomial inverse integrating factors of quadratic differential systems and other results[D]. Universitat Autonoma de Barcelona,2006：33-110.

[15] AL-DOSARY K I T. Inverse integrating factor for classes of planar differential systems[J]. International Journal of Mathematical Analysis,2010,4(29):1433-1446.

[16] HU Y, CHEN Y. The inverse integrating factor for some classes of n-th order autonomous differential systems[J].Journal of Mathematical Analysis and Applications,2015,423(2):1081-1088.

[17] ALGABA A, GAMERO E, GARCIA C. The integrability problem for a class of planar systems[J]. Nonlinearity,2009,22(2):395-420

[18] COLL B, GASULL A, PROHENS R. Differential equations defined by the sum of two quasi-homogeneous vector fields[J]. Canadian Journal of Mathematics,1997,49(2):212-231.

(责任编辑： 康 锋)

Inverse Integrating Factors of Quasi-Homogeneous Planar Polynomial Systems

HANMeijia,HUANGTusen

(School of Sciences, Zhejiang Sci-Tech University, Hangzhou 310018, China)

The inverse integrating factor is an important tool to study the integrability problem of planar polynomial systems. For a quasi-homogeneous polynomial system, the existence of polynomial inverse integrating factor is proved by using the generalized Euler’s theorem, and the explicit expression is given. For a polynomial system defined by the sum of two quasi-homogeneous polynomial systems, a sufficient condition for the existence of a polynomial inverse integrating factor is given. Then, the computing formulas of inverse integrating factors for several special polynomial systems are given. The computing examples illustrate that the results in this paper generalize the existing conclusions.

quasi-homogeneous polynomial system; polynomial inverse integrating factor; quasi-homogeneous decomposition

10.3969/j.issn.1673-3851.2016.11.024

2016-03-02

浙江省自然科学基金项目(LY15A010021)

韩美佳(1992-)，女，山东青岛人，硕士研究生，主要从事微分方程定性理论方面的研究。

O175.14

A

1673- 3851 (2016) 06- 0939- 06 引用页码： 110801