一种新的海洋水下溢油泄露预报方法
于博骞, 余建星, 李志刚, 苗春生, 刘 杰, 赵志恒
(1.天津大学 水利工程仿真与安全国家重点实验室, 天津 300072; 2.高新船舶与深海开发装备协同创新中心,上海 200240;3.海洋石油工程股份有限公司, 天津 300451)
一种新的海洋水下溢油泄露预报方法
于博骞1,2, 余建星1,2, 李志刚1,3, 苗春生1,3, 刘 杰1,2, 赵志恒1,2
(1.天津大学 水利工程仿真与安全国家重点实验室, 天津 300072; 2.高新船舶与深海开发装备协同创新中心,上海 200240;3.海洋石油工程股份有限公司, 天津 300451)
采用FLUENT软件中的VOF模型和DPM模型的联合模型对水下原油泄露进行分析。建立变化的环境流载荷条件,模拟了不同泄漏速率、不同泄漏口径下的水下溢油过程。分析了泄漏口径变化对溢油上浮时间的影响以及溢油上浮时间分别与泄漏速度和漂移距离之间的关系。
VOF模型;DPM模型;FLUENT;水下溢油
0 引言
近年来我国水下原油开采逐渐成为解决能源问题的重要手段,水下溢油事故的危险性也逐渐被世界所认识。水下溢油事故在导致大量财产损失的同时还会导致海洋污染,进而威胁海洋生态平衡。水下溢油过程的模拟不但能够尽早确定水下溢油点,同时可为后期进行安全抢修、治理环境污染等问题提供良好的技术支持,同时也是实现安全生产的重要手段。
对水下油气泄漏导致的羽流问题的研究开始很早,国外研究主要基于试验物理学和不断修正的理论公式,在研究过程中提出了很多理论模型:Deepblow模型[1],Vdrop模型[2]以及CDOG模型[3]。从事相关研究的学者们纷纷提出模型的改进方案使其最大限度的接近真实情况。其中CDOG模型起步较早,并以大型试验水池Deepspill试验场中的试验数据为依据[4],通过试验数据,不断验证和改进粒子直径的分布情况,从而获得了良好的适用性[5,6]。国内对水下油气泄漏过程的研究是对国外研究的吸收和再现,主要基于油气混合的CDOG模型基本理论[7],将大型试验水池数据与模型模拟结果进行对比[8]。虽然对油气混合泄漏模型的研究已经很完善,但是对一些重要的预测参数的确定还存在一定的困难。同时,在面对复杂海况和一般水深与浅水中的油气泄露问题上缺少有效的研究和试验作为支撑,使得重要参数的选取缺少依据。
该文主要是以FLUENT软件的DPM模型和VOF模型为基础,采用羽流速度作为对流扩散起始点,并引用Yapa(2003)提出的粒子分布和粒子特征直径的分布规律进行有限元模拟。根据环境载荷的特点,将环境流场随水深变化的速度拟合成二次曲线,并以此建立边界条件。通过多组计算模拟,得出较为全面的结果用来分析浅水溢油问题的几个关键参数——溢油时间、漂移距离、环境流速之间的关系。
1 模型基本理论
VOF模型是计算流体力学软件FLUENT用来处理多相流问题的模型,其基本原理是:在欧拉网格内添加一个关于多相流的参数,用来描述一个单元格内的第二相所占比例,之后进行差值。这种模型对于模拟原油扩散时生成浮力羽流的过程很不方便,原油液滴的破碎导致大量离散的小液滴存在,其整体的物理性质与原油相差甚远。使用离散相模型DPM可以较好地模拟泄漏过程中原油液滴离散的运动状态,同时又可以有效地模拟原油液滴与环境流的交互作用。
1.1 VOF模型
VOF模型是多相流模型中的一种,其中较为广泛的应用就是在进行明渠流模拟时,在FLUENT软件的VOF模型中使用明渠流定义重要的模型参数。VOF模型基本原理如下[9]:
质量守恒方程:
(1)
动量守恒方程:
(2)
组分质量守恒方程
(3)
式(1)~式(3)中:αi为各项体积分数,∑αi=1;ρ为密度; v为速度;E为流体微团的总能;keff为有效导热系数;S为源项。
VOF模型主要用于解决互不相容的两相混合问题,适用于较大气泡上浮等问题,用来模拟水下溢油过程中的环境流与海面空气的相互作用模型。
1.2 DPM模型
DPM离散相模型主要用来处理粒子与气泡富集的汽相或液相中的各种模拟问题。基本的平衡方程为拖曳力和惯性力平衡方程:
(4)
其中拖曳力项:
(5)
(6)
式(6)中:αi为常数[10]。
拖曳力系数的计算方法与Yapa[11]的不同大小液滴最终速度的计算方法存在差异,但误差稳定且较小,因而此方法依然有效。
同时,离散相模型不能考虑除去拖曳力外的作用形式,对于湍流引起的夹带影响考虑不全导致整体的速度降低较缓慢进而出现较快的上浮速度,是此模型的固有缺陷。
2 建模过程
建立模型为二维水池,上部充满空气下部充满海水,并划分标准网格。因为在泄漏过程中采用的是DPM模型模拟水下原油的泄漏过程,因而DPM泄漏口为定义在水池底部的injection模块。不必使用特定的泄漏口,如此大大简化了建模过程中关于泄漏口部分的网格细化工作。模型选取VOF模型和DPM模型激活,VOF模型中选择明渠流模型,对部分波浪影响的泄漏模拟也可以激活VOF中的波浪模型。
Johansen关于粒子分布形式进行了讨论并得出韦伯分布更适合作为原油泄漏的分布形式[6]:
(7)
式中:di为中值直径;ki=-ln(1-Vi)。FLUENT软件中,粒子的分布形式也包含韦伯分布形式。同时可以设置韦伯分布的几个特征值:最大直径、最小直径、平均直径。设置粒子喷射的质量速度就可以隐含喷射粒子总数,设置粒子初始速度来模拟泄漏口速度。
在材质中设置海水密度、粘度系数等参数。泄漏粒子材料类型中设置原油的基本特性密度。在计算域参数设置中设置环境参考密度以形成浮力等惯性力。
进行16组计算,每组的试验条件分为三部分,分别为海面流速、中间层流速和底层流速,输入数据见表1。边界条件采用速度边界条件模拟层流边界条件,实现方法采用自定义UDF和速度边界条件。UDF使用的命令主要为DEFINE_INIT ( name, d),DEFINE_PROFILE ( name, t, i),采用二次插值形式形成边界速度水深函数,初始化速度云图如图1,边界速度分布图如图2所示。
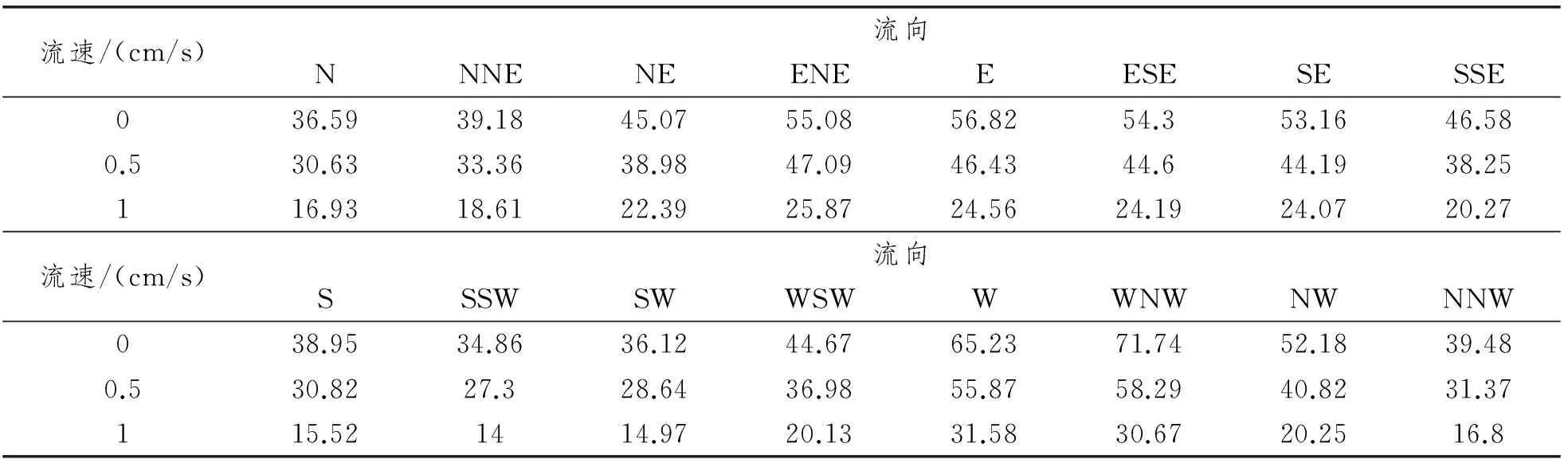
表1 某油田海流及流速流

图1 初始化速度云图
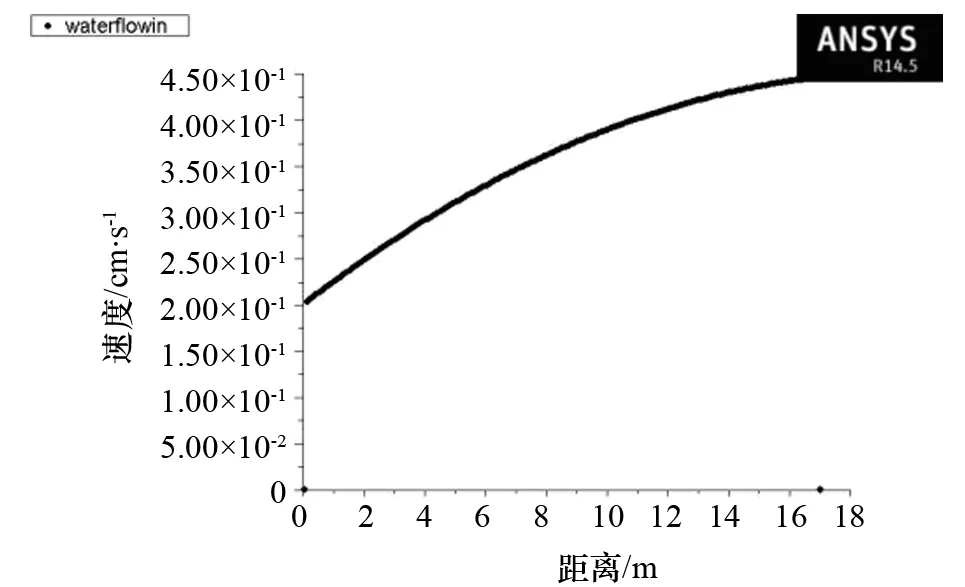
图2 边界速度分布图
3 计算结果
(1) 初步模拟采用固定泄漏口5 cm,泄漏速度为10 m/s,变换边界条件进行模拟。模拟结果如图3、图4所示。

图3 ENE向原油抵达海面分布图

图4 SSW向原油抵达海面分布图

图5 漂移范围
从图3、图4中可看出:两个模型耦合计算的效果与真实溢油过程相似,既可以完成对原油离散成液滴过程的模拟又可以实现对横流与喷射流之间形成漩涡和扩散的模拟。综合计算结果绘制雷达图如图5所示。
(2) 对上、中、下三层速度的漂移范围和漂移时间进行拟合,线性拟合结果见表2,泄漏范围与泄漏时间拟合结果如图6所示。其中影响因子为单位流速增加导致的漂移范围或上浮时间的变化量。
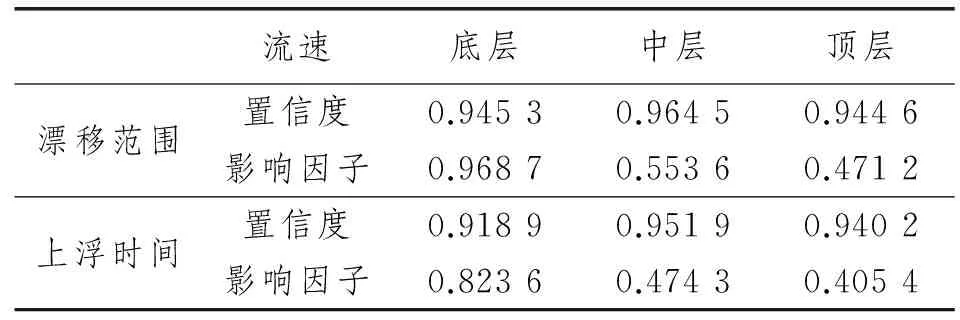
表2 线性拟合结果

图6 泄漏范围与泄漏时间拟合结果
固定口径固定速度下变换环境载荷的泄漏结果中泄漏时间和漂移距离的关系接近线性。整体的置信度也较高。
(2)选取几组边界条件作为模拟条件,并变换泄漏口直径进行模拟。泄漏口大小分别取20 mm、40 mm、100 mm、200 mm、300 mm,泄漏速度为26.917 m/s。计算结果见表3,泄漏时间与漂移距离如图7所示。

表3 计算结果

图7 泄漏时间与漂移距离
由图7可知,当泄漏口径逐渐变大时,相对漂移距离和泄漏时间都在减小,而置信度整体上都呈现出降低的趋势。在泄漏口径变大的过程中残差波动变大,泄漏时间与漂移距离的线性关系也不明显,受泄漏环境影响也逐渐降低。这可能是因为随着泄漏口径逐渐增大,喷射口对整体泄漏环境的影响变大,从而导致环境速度变化较大。
4 结论
使用VOF模型和DPM模型耦合进行水下原油泄漏过程的计算是可行的,能够模拟出原油泄漏过程中破碎成粒子的运动,同时也能模拟出环境流与喷射口之间交互作用导致的湍流和漩涡问题,以及环境流与喷射口的动量交换引起的速度场变化。然而在模拟过程中还存在一些问题,如拖曳力系数计算公式比较老旧,湍流问题受到网格粗细的限制,DPM模型不能考虑到羽流夹带问题导致粒子速度降低缓慢,粒子泄漏数量不是无限的,泄漏过程时间增加会导致粒子数量超过可接受的最大量等等。但是对于解决对流扩散阶段的模拟是可行的。应用于粒子直径变化不大,粒子碰撞融合与粒子破碎不明显的扩散阶段比较有优势。
[1] Johansen Ø. Deepblow-a Lagrangian Plume Model for Deep Water Blowouts[J]. Spill Science & Technology Bulletin, 2000,6(2): 103-111.
[2] Zhao L,Torlapati J, Boufadel M C,et al. VDROP: A comprehensive model for droplet formation of oils and gases in liquids-Incorporation of the interfacial tension and droplet viscosity[J]. Chemical Engineering Journal, 2014,253: 93-106.
[3] Zheng L, Yapa P D, Chen F. A model for simulating deepwater oil and gas blowouts-Part I: Theory and model formulation[J]. Journal of Hydraulic Research, 2003, 41(4): 339-351.
[4] Chen F and Yapa P D. A model for simulating deep water oil and gas blowouts-Part II: Comparison of numerical simulations with “Deepspill” field experiments[J]. Journal of Hydraulic Research, 2003,41(4): 353-365.
[5] Brandvik P J. Droplet breakup in subsurface oil releases-Part 1: Experimental study of droplet breakup and effectiveness of dispersant injection[J]. Marine Pollution Bulletin, 2013,73(1): 319-326.
[6] Johansen Ø, Brandvik P J, Farooq U. Droplet breakup in subsea oil releases Part 2: Predictions of droplet size distributions with and without injection of chemical dispersants[J]. Marine Pollution Bulletin, 2013,73(1): 327-335.
[7] 段丽琴. 海底溢油的归宿及输移扩散行为[J]. 海洋科学, 2013(6): 113-120.
[8] 陈海波. 水下溢油数值模拟研究[J]. 海洋工程, 2015(2): 66-76.
[9] 于勇,张俊明,姜连田.FLUENT 入门与进阶教程[M].北京:北京理工大学,2010.
[10] Morsi S A, Alexander A J. An Investigation of Particle Trajectories in Two-Phase Flow Systems[J]. Fluid Mech., 1972,55(2):193-208.
[11] Zheng L, Yapa P D. Velocity of Spherical and Nonspherical Bubbles/Droplets[J]. Journal of Hydraulic Engineering, 2000,126(11): 852-854.
A New Marine Underwater Oil Spill Leak Prediction Method
YU Bo-qian1,2, YU Jian-xing1,2, LI Zhi-gang1,3, MIAO Chun-sheng1,3, LIU Jie1,2, ZHAO Zhi-heng1,2
(1.State Key Laboratory of Hydraulic Engineering Simulation and Safety, Tianjin University, Tianjin 300072, China; 2.Collaborative Innovation Center of High and New Ship and Deep Sea Development Equipment, Shanghai 200240, China; 3.Offshore Oil Engineering Limited Company, Tianjin 300451, China)
This article analyzes the oil spill with the VOF model and DPM model in the FLUENT. This model is used to do several simulations in different conditions. The outcome of this model was used to discuss the influence of the opening radius at release point and the magnitude of the jet velocity on the range and time of the oil spill.
VOF model; DPM model; FLUENT; underwater oil spill
2015-10-29
国家自然科学基金(51379145),国家自然科学基金(51239008),国家重点基础研究发展计划资助(2014CB046806) 。
于博骞(1991-),男,硕士研究生。
1001-4500(2016)05-0021-06
P75
A

