自升式钻井平台悬臂梁结构动态响应分析

窦培林， 唐建飞， 李晓东 ，裴满意

(江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003)



自升式钻井平台悬臂梁结构动态响应分析

窦培林， 唐建飞， 李晓东 ，裴满意

(江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003)

悬臂梁结构是自升式钻井平台钻井模块的重要配置，直接影响平台的钻井能力。利用MSC.Patran&Nastran软件对某350 ft自升式钻井平台悬臂梁结构进行动态响应分析，建立了悬臂梁结构的有限元模型，在悬臂梁最大外伸工况下，分析得到结构的前8阶固有频率和振型。随后在模态分析的基础上利用模态法对悬臂梁进行瞬时动态响应分析，得到了结构在瞬态载荷作用下的动力响应。结果表明：动载荷对悬臂梁结构影响比较明显，在进行悬臂梁结构分析时必须考虑钻井过程中动载荷对结构的影响。研究结果对悬臂梁结构分析及优化设计具有一定的指导意义。

自升式钻井平台；悬臂梁；模态分析；瞬时动态响应分析

0 引言

海洋平台作为海上资源开发的重要装备，在油气勘探开发中发挥着重要作用。其中，自升式钻井平台由于其操作灵活、定位能力强、适用水域广、可重复使用等优点，在大陆架海域油气勘探开发中得到了广泛应用。悬臂梁结构作为自升式钻井平台的重要配置，其主要功能是通过调整自身外伸距离以及钻台的横向移动，实现井口位置的变化和钻丛式井的目的，能有效地扩大自升式钻井平台的钻井作业范围[1-3]。

目前，悬臂梁的结构分析主要局限于静力分析，任宪刚等[4]介绍了当今国际上常用的三种悬臂梁型式，对比分析了三种悬臂梁优缺点、结构特点和作业范围，列举了一个悬臂梁具体的设计实例，阐述了其设计方法，在不同工况下，对悬臂梁进行了有限元分析。刘祥建等[5]以大连船舶重工自主研发的DSJ-300自升式钻井平台为目标，详细介绍了悬臂梁结构研究分析的方法，通过有限元分析，得到了该平台悬臂梁结构的应力图。刘宇等[6]利用有限元软件ANSYS对海洋平台悬臂梁进行了强度计算，得到了悬臂梁位移和应力云图，在平台建造码头对悬臂梁进行了现场强度测试试验，并将有限元计算结果与实际测试结果进行了比较分析。在实际工作过程中，悬臂梁要承受钻井设备的振动以及变化的钻井载荷等动载荷的作用，目前对悬臂梁进行动态分析开展的相关研究比较少，因此关注其动态特性在工程上是比较有意义的。为了保证悬臂梁具有足够的可靠性，必须在设计的时候对其进行动态响应分析。

以某350 ft水深作业的自升式钻井平台的悬臂梁结构为研究对象，该平台如图1所示。采用有限元软件MSC.Patran&Nastran，建立了悬臂梁结构有限元模型，在悬臂梁最大外伸工况下，对悬臂梁进行了动态响应分析。研究结果可为同类结构的动态响应分析提供参考，对该型悬臂梁后续结构优化设计也具有一定的指导意义。

图1 自升式钻井平台

1 结构动力学分析理论基础

悬臂梁结构属于多自由度结构，其多自由度结构系统结构动力学基本方程如下：

(1)

对于海洋平台和船舶等海洋结构物的动力分析过程中，由于外摩擦很小，系统的阻尼主要是结构阻尼，结构系统的阻尼矩阵[C]通常可以忽略不计[7]。悬臂梁结构动力响应分析实质就是求解悬臂梁结构动力学基本方程的过程。

悬臂梁结构动力响应分析首先是进行结构的模态分析，得到悬臂梁结构的固有频率和振型，为后续瞬时动态响应分析提供重要的参数。在模态分析的基础上，计算悬臂梁在瞬时冲击载荷F(t)作用下的瞬时动态响应。一般动态响应分析方法有解析法和有限元法，对于悬臂梁这类自由度结构常用有限元法进行动态响应分析。

2 悬臂梁有限元模型

2.1 悬臂梁有限元模型的建立

该文以某船厂350 ft水深作业的三角型自升式钻井平台悬臂梁结构为研究对象，其侧视图如图2所示，悬臂梁主要设计参数见表1。

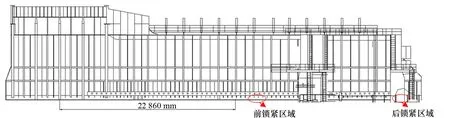
图2 悬臂梁结构侧视图

表1 悬臂梁设计基本参数

图3 悬臂梁结构有限元模型

该悬臂梁结构模型为左右对称结构，模型的所有板架结构及强型材腹板均采用四边形或三角形板单元模拟，其它骨材、扶强材及强型材面板均采用梁单元模拟。悬臂梁结构所采用的材料为高强度或超高强度钢，纵向大梁与井架横梁采用EQ56超高强度钢，其余结构采用DH36、EH36高强度钢，杨氏模量E=210 GPa，泊松比μ=0.3，密度ρ=7.85×10-6kg/mm3，EQ56超高强度钢屈服极限σ1=550 MPa，EH36、DH36(船用高强度结构钢)屈服极限σ2=355 MPa，悬臂梁结构有限元模型如图3所示。

2.2 边界条件

自升式平台悬臂梁结构在生产作业过程中通过锁紧装置控制进行定位，包括前锁紧装置和后锁紧装置，其作用是在悬臂梁到达井口位置后对其进行固定，这两处为固定约束，因此在有限元计算中该两处的边界条件均采用固定约束进行模拟。

3 结构动力响应分析

悬臂梁在工作过程中工况较为复杂，根据静态分析结果，危险工作工况发生在悬臂梁最大外伸的情况下，因此该文以悬臂梁外伸距离最大工况进行动力响应分析。

3.1 模态计算及分析

考虑了悬臂梁结构实际工作状态的边界条件，采用MSC.Nastran有限元分析软件中的Lanczos Method(兰索士法)[9]对自升式钻井平台悬臂梁结构在极限井位工况下的模态进行了分析。在多自由度系统中，低阶模态对结构的振动特性起主要作用，阶数越高其影响越小，高阶模态几乎无影响，因此该文提取了悬臂梁结构的前8阶模态振型，如图4所示，模态频率见表2。

图4 悬臂梁前8阶模态振型

表2 悬臂梁前8阶模态频率

由前8阶振型图可以看出：第1阶振型其振动型式表现为悬臂梁整体做大幅度左右摆动，无其他明显振动型式；第2阶振型其振动型式主要表现为钻台区外横梁强烈的前后摆动，并带动钻台区左右两侧的大梁摆动；第3阶振型其振动型式主要表现为钻台区大幅度左右摆动，悬臂梁整体伴有轻微的摆动；第4阶振型其振动型式主要表现为悬臂梁整体弯曲；第5阶振型其振动型式主要表现为钻台区两侧的大梁左右摆动，并带动钻台区外横梁的前后摆动；第6阶振型其振动型式主要表现为钻台区左右两侧的大梁左右摆动；第7阶振型其振动型式主要表现为钻台区外横梁的扭转运动，钻台区两侧的大梁伴有轻微的左右摆动；第8阶振型其振动型式主要表现为悬臂梁结构整体比较强烈的扭转运动。

通过悬臂梁结构的模态分析可以看出：除了悬臂梁结构整体表现出的摇摆、弯曲及扭转运动外，其局部振动主要发生在钻台区，此处为钻井载荷主要承受区域，刚度偏弱，为危险区域，建议采取加强措施加强该区域两侧大梁及外侧横梁的刚度。

3.2 瞬态动力响应分析

瞬态动力学分析也叫时间历程分析，是用来计算结构强迫动力响应的一种方法。瞬态动力响应的目的是计算结构在随时间变化的激励载荷作用下的响应(应力、应变、力)，为结构的优化设计奠定基础。对于瞬态动力学分析，MSC.Nastran中提供了模态法和直接法[9]两种求解方法，对悬臂梁结构瞬态动力学分析采用模态法进行求解。

3.2.1 冲击载荷确定

在正常钻井工作过程中有时会出现“猛提、猛刹”的操作，这一动作会对结构体产生较大的瞬时冲击载荷，该文以悬臂梁最大外伸钻井过程中的特殊工作状态(“猛提、猛刹”)[8]为计算工况进行瞬态分析，该工况下的载荷与时间曲线如图5所示。

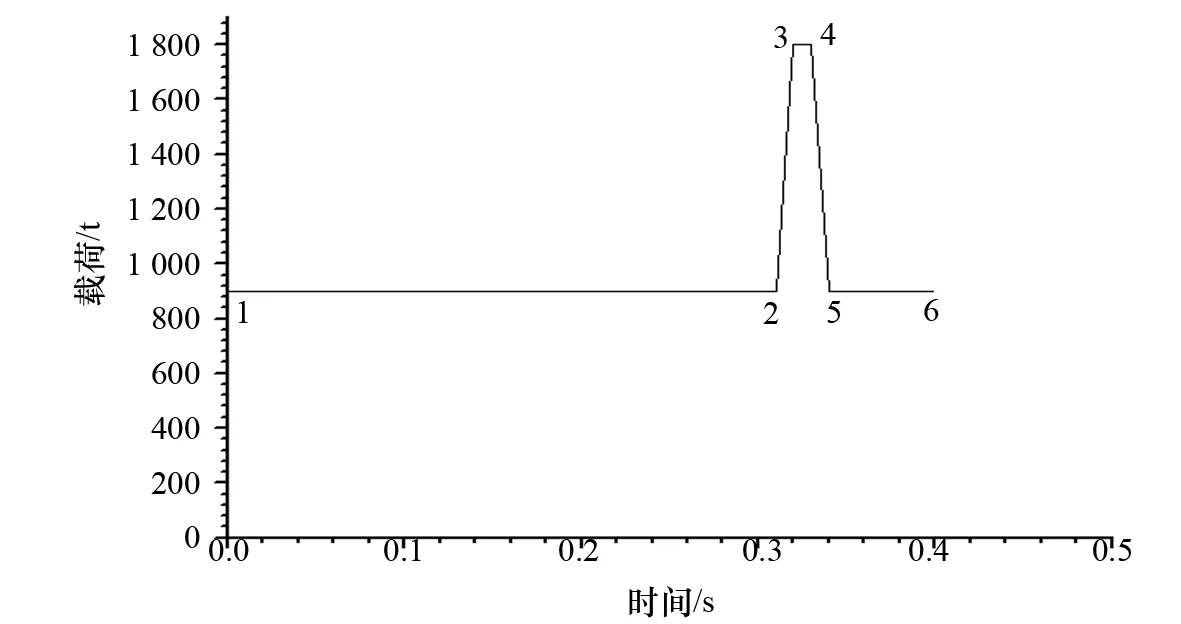
图 5 “猛刹、猛提”工况载荷时间曲线

图5描述了悬臂梁瞬时动态响应分析试验加载的时间历程，将该时间历程施加于悬臂梁节点以计算悬臂梁在“猛刹、猛提”工况下所产生的瞬时冲击载荷的响应，包括：1～2阶段为载荷施加的初始阶段，悬臂梁从0～0.31 s始终承受900 t恒定载荷的作用；2～3阶段为从0.31 s开始载荷瞬间以坡面的形式陡然增加至1 800 t；3～4阶段悬臂梁承受1 800 t恒定载荷的作用；4～5阶段载荷从0.328 s～0.34 s快速降至原来的900 t；5～6阶段悬臂梁继续承受900 t不变的载荷。

3.2.2 时间步长的确定

时间步长的选取主要取决于计算精度，即在满足计算精度要求的前提下，选取尽可能大的时间步长，这样可以节省计算时间。在结构分析中，通常是前几阶振型对结构的影响比较大，更高阶振型的影响可以忽略。在悬臂梁瞬时动态响应分析时，时间步长Δt与结构的最高频率fmax满足式(2)时其解的精度比较合理。

(2)

由模态分析结果可知fmax=6.195 Hz，所以取Δt为0.008 s为瞬时动态响应分析的时间步长。

3.2.3 结果与分析

利用MSC.Nastran对悬臂梁进行瞬态动力响应分析，得到了悬臂梁结构动力响应结果，如图6、图7所示。

图6 应力云图

图7 动位移响应图

图6(a)为悬臂梁结构整体应力云图，图6(b)为图6(a)的细节放大图，从结构的整体应力云图中可以看出，悬臂梁整体结构应力水平较低，最大集中应力发生在悬臂梁前端锁紧装置处，如图6(b)所示，其值为489 MPa，相比于静力分析要大31.8%(静力计算最大应力值为371 MPa)，说明悬臂梁在该特殊工况下受到的瞬态冲击载荷对局部结构的应力影响较为明显。“猛提、猛刹”工况是钻井过程中的一种特殊工况，操作过程中应尽量避免，但在设计过程中必须考虑特殊工况下动载荷对结构的影响，对局部结构进行加强，以免悬臂梁发生动力失稳破坏。悬臂梁动位移响应图如图7所示。

由图7可以看出，随着时间的推移，悬臂梁末端(节点51 637)的位移随之增大。在0.31 s前，悬臂梁末端的位移先快速增大，在经历0.2 s后变化速度平缓。在0.3 s后由于“猛提、猛刹”的现象引起大钩载荷急剧增加导致悬臂梁末端位移曲线迅速上升并达到极值228.01 mm，比静力分析下变形值大42.5%(静力计算最大变形值为160 mm)。

4 结论

该文在悬臂梁最大外伸工况下利用MSC.Patran&Nastran软件对其进行了动态响应分析。首先进行了模态分析，并以“猛提、猛刹”特殊工况进行了瞬态动力响应分析，得到如下结论：

(1) 通过悬臂梁的模态分析，得到了悬臂梁结构的前几阶固有频率和振型，为瞬时动态响应分析及其他动力响应分析提供了重要的参数。

(2) 通过悬臂梁结构瞬态动力响应分析，得到了“猛提、猛刹”工况下结构的动力响应。动载荷对悬臂梁结构的影响比较大，最大动应力比静力分析结果大31.8%，最大动位移比静力分析变形值大42.5%。因此，在进行悬臂梁结构分析时必须考虑钻井过程中动载荷对结构的影响。

悬臂梁结构的动力响应分析为同类结构的动态响应分析提供了参考，也对该型悬臂梁结构后续优化设计及工程实际操作有一定的指导意义。

[1] 陈宏, 李春祥. 自升式钻井平台的发展综述[J]. 中国海洋平台, 2007,22(6):1-6.

[2] 王龙庭, 王西录, 梁会高, 等. 国外自升式悬臂梁钻井平台结构特点[J]. 海洋石油, 2009,29(4):89-93.

[3] 钱亚林, 薄玉宝. 自升式悬臂梁钻井平台初探[J]. 上海造船, 2009，25(1):15-18.

[4] 任宪刚, 白勇, 贾鲁生. 自升式钻井平台悬臂梁研究[J]. 船舶力学, 2011，15(4):402-409.

[5] 刘祥建, 戴挺, 张佳宁, 等. 自升式平台悬臂梁结构分析方法的研究[C]. 中国钢结构协会海洋钢结构分会2010年学术会议暨第六届理事会第三次会议, 河南洛阳, 2010.

[6] 刘宇, 颜廷俊, 魏辽, 等. 海洋作业平台悬臂梁强度计算与试验分析研究[J]. 石油机械, 2012，40(5):53-56.

[7] 杨旭东, 张世联. 有限元分析结构瞬态响应中的结构阻尼问题[J]. 中国海洋平台, 2004，19(2):32-36.

[8] 付海龙. 石油钻机井架动态响应研究[D]. 大庆：大庆石油学院，2005.

[9] 龙凯.Patran2010与Nastran2010有限元分析从入门到精通[M].北京：机械工业出版社,2014.

Dynamic Response Analysis for Cantilever Beam of Jack-up Platform

DOU Pei-lin, TANG Jian-fei， LI Xiao-dong, PEI Man-yi

(Jiangsu University of Science and Technology, Jiangsu Zhenjiang 212003， China)

Cantilever beam structure is an important configuration of drilling modules of jack-up drilling platform. It has a direct influence on the drilling capacity of platform. The finite element model of cantilever beam structure of 350ft jack-up drilling platform was estabished by MSC.Patran&Nastran software to analyze the dynamic response. Firstly, the structure 8 natural frequencies and vibration modes in the condition of maximum cantilever overhang were got. Then, adopting modal method to have a transient dynamic response analysis on the basis of modal analysis. The dynamic response of the structure under the action of transient loads. It can be found that dynamic loads have more obvious influence on cantilever beam structure. Therefore, dynamic loads must be considered when analyzing cantilever beam structure. It has a certain guiding significance to cantilever beam structure analysis and optimization design.

jack-up drilling platform； cantilever beam； modal analysis； transient dynamic response analysis

2015-08-24

窦培林(1964-)，男，教授。

1001-4500(2016)05-0057-06

P75

A