一种基于性能的抗震设计的Pushover分析方法

李沛豪，刘崇奇

(浙江工业大学 建筑工程学院，浙江 杭州 310014)



一种基于性能的抗震设计的Pushover分析方法

李沛豪，刘崇奇

(浙江工业大学 建筑工程学院，浙江 杭州 310014)

论述了一种以顶层位移作为性能指标的弹塑性Pushover分析方法用于基于性能的抗震分析，并且编制了相应的Matlab程序.为验证分析方法的科学性和可靠性，用Pushover程序对双层单跨、双层双跨的两榀平面钢框架作计算分析，且与其试验数据进行对比.结果显示：分析结果与试验数据的荷载—位移曲线基本吻合，误差小于14%，表明Pushover分析方法和程序可靠.并以Pushover方法作为抗震性能的分析工具对一榀三层四跨框架做了抗震分析，显示了Pushover方法的适用性.

基于性能的抗震设计；Pushover分析；钢框架

目前，基于性能的抗震设计的理论研究和应用已经取得巨大进展.基于性能的抗震设计即根据结构重要性和用途确定的不同的性能目标，提出不同的抗震设防水准，使设计的结构在使用期内和地震影响下具备预期的功能以满足不同的性能目标要求[1].结构位移是衡量结构抗震性能的重要参数[2].在众多的抗震分析计算方法[3-4]中，Pushover方法具有较强的实用性.高依强等[5]采用Pushover方法对双柱式桥墩作了抗震性能分析；潘毅等[6]研究了Pushover方法在既有建筑安全性鉴定中的应用；张文明等[7]通过一砼框架算例对比验证了Pushover方法在抗震性能评估中的可靠性和实用性；刘畅等[8]对多层偏心结构的Pushover分析作了研究.笔者论述了一种以顶层位移作为性能指标的非线性静力弹塑性Pushover分析方法，通过将两榀框架的分析结果与试验数据进行比对，验证其可靠性，并将其应用于一榀三层四跨框架的抗震分析.

1 Pushover分析方法及程序编制

Pushover分析是在侧向单调加载模式下对结构的作静力弹塑性分析，即在结构上施加某种递增的模拟地震水平惯性力作用的侧向力，由结构的整个变化过程分析结构的内力、变形和耗能特性[9].

考虑到地震荷载作用下梁柱构件之间的半刚性连接、结构的非线性变形以及二阶P—Δ效应影响，将刚度矩阵设置为

K=SeCe+SgCg

(1)

式中：Se，Sg分别为一阶弹性刚度矩阵和二阶几何刚度矩阵；Ce，Cg分别为相应的考虑半刚性连接的修正系数矩阵，由无量纲的刚性系数r组合而成.

其半刚性连接时经修正的一阶弹性刚度矩阵为

(2)

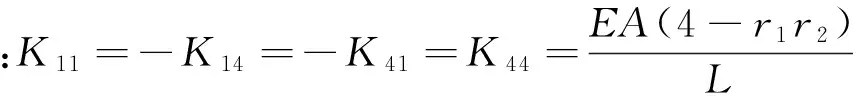
经修正的二阶几何刚度矩阵为

(3)

由图1可知：刚性系数r(0≤r≤1)与塑性转角(θ-α)有关，表示构件在端点处的转动能力，用以衡量截面的塑性程度.其计算公式可定义为

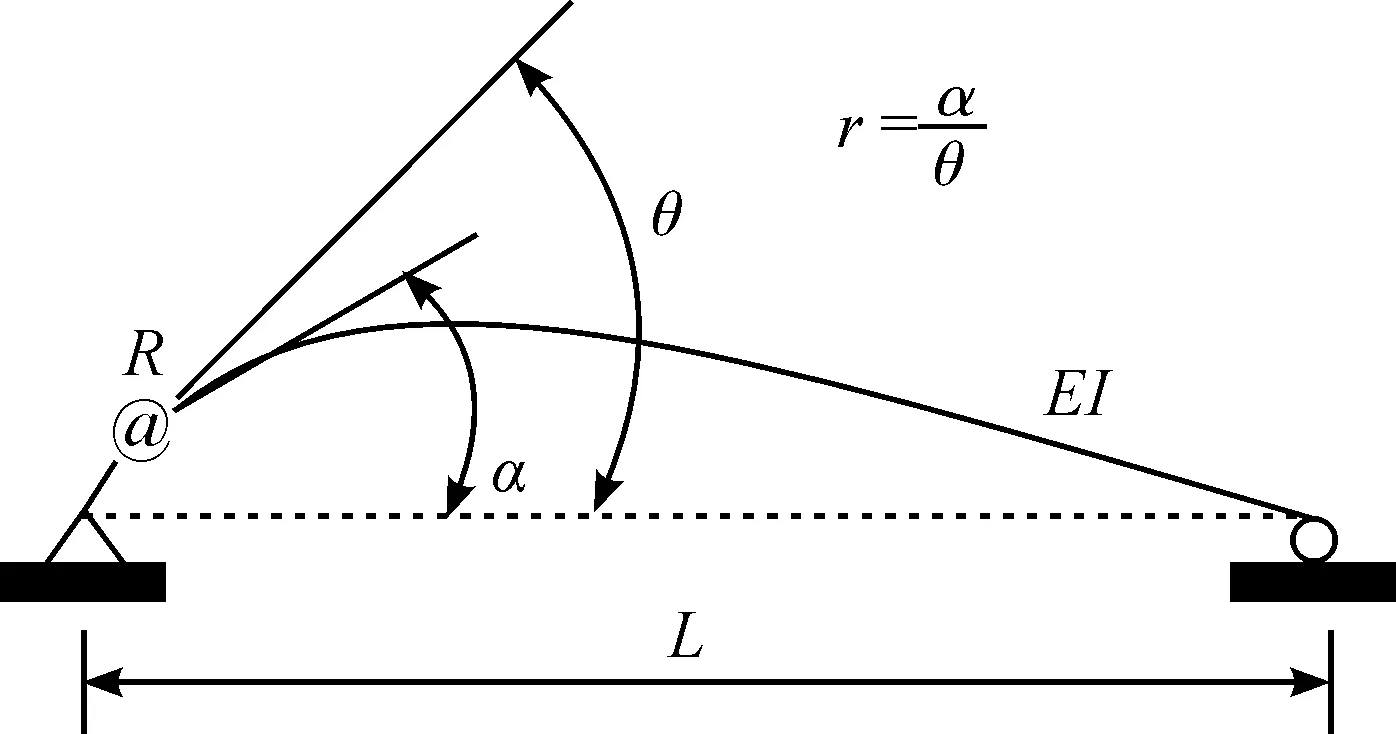
图1 半刚性连接Fig.1 Seismic-rigid moment-connection

(4)

式中：EI和L分别为弯曲刚度和构件长度；R(0≤R≤∞)为转动刚度.

将截面出现塑性变形之后的弯矩—曲率关系简化为图2中的实曲线.图2中My，Mp分别为纯弯状态下截面刚出现塑性变形和完全塑性时的弯矩；φy为截面刚发生塑性变形时的曲率；φp为刚形成塑性铰时的曲率；φu为截面极限曲率.该曲线方程可表示为

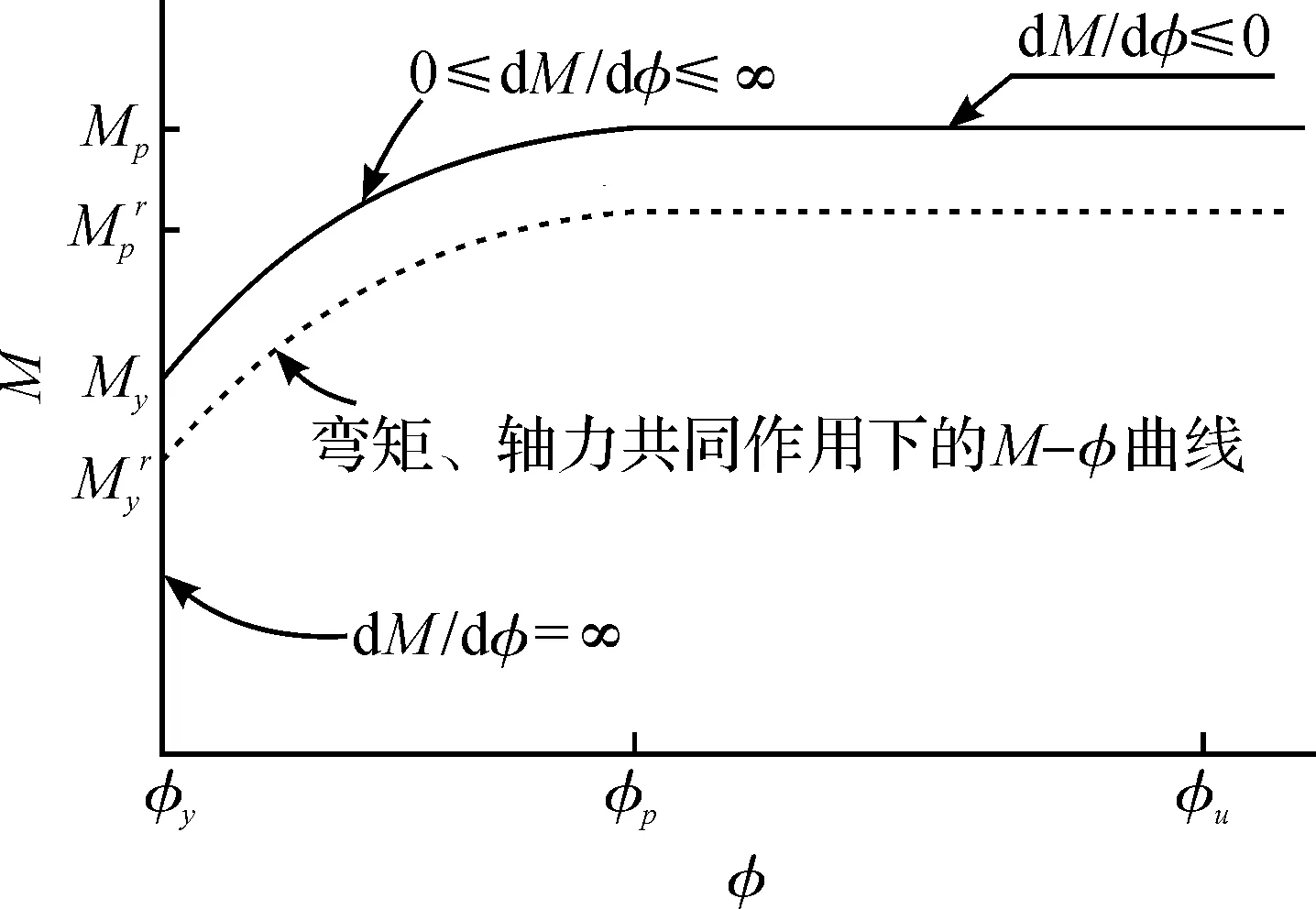
图2 非弹性阶段的弯矩—曲率关系Fig.2 Post-elastic moment-curvature relation

(5)

则转动刚度R为

(6)

其中φ为

(7)

上述本构模型仅适用于理想的纯弯状态，考虑弯矩和轴力共同作用时则由ξ值判定截面的弹塑性状态，ξ的计算表达式为

(8)

式中Np为单轴受力状态下截面完全屈服时的轴力.ξ值与截面弹塑性状态的的对应关系见表1.

表1 ξ值与弹塑性状态的对应关系1)

注：1)fs=Mp/My，即截面形状系数.

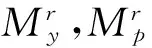
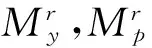
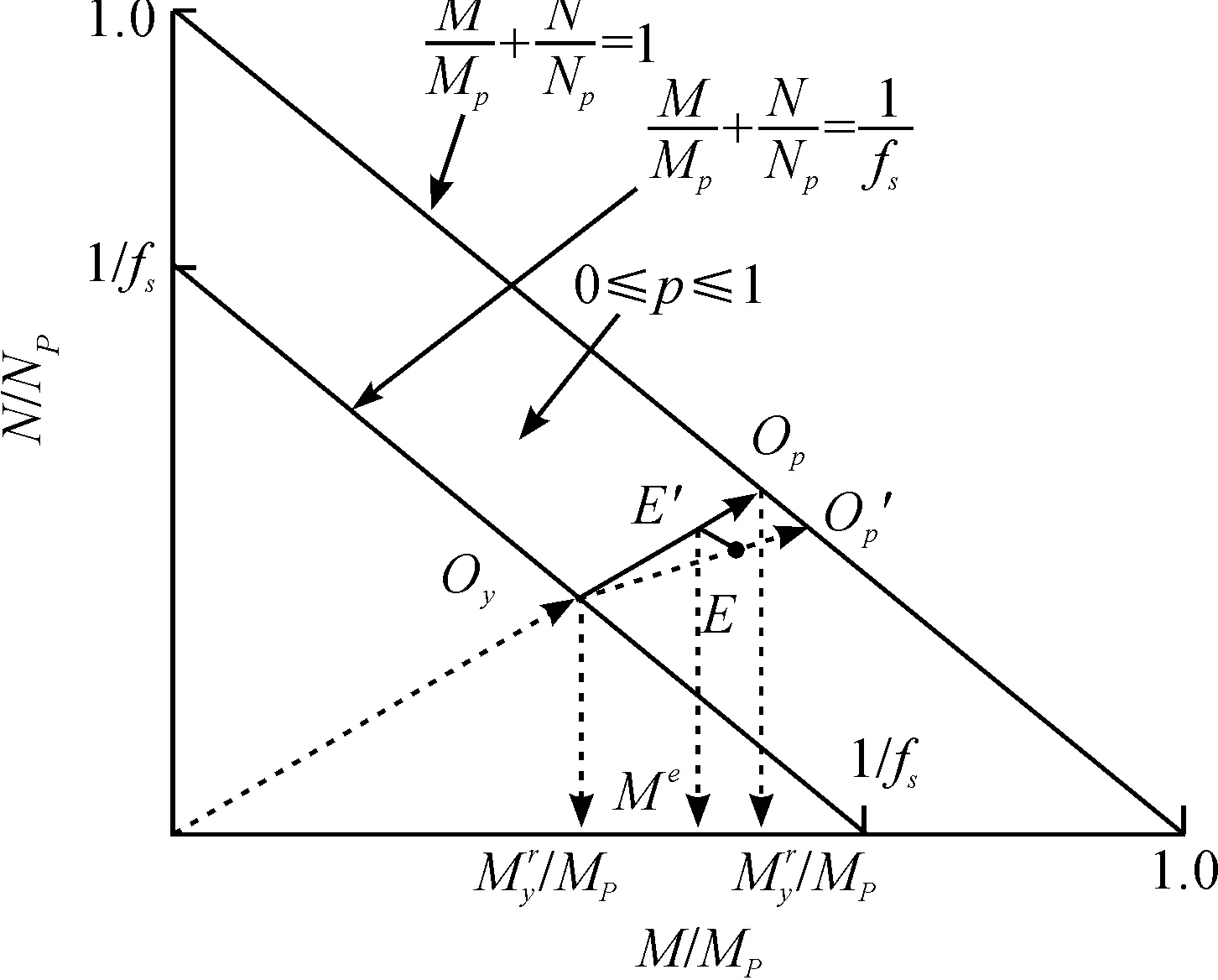
图3 弯矩、轴力共同作用下的弹塑性状态Fig.3 Plasticity under combined bending moment and axial force

(9)

(10)

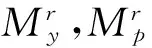
实际分析过程中，N/M的比值并不一直保持恒定，可在图3中过状态点E作平行于边界线的直线EE′交直线OyOp于E′，则E′在横坐标上的投影值乘以Mp即为等效弯矩值Me[10]，其表达式为

Me=My·ξ·fs

(11)

Pushover分析过程中，首先将结构的自重恒荷载和活荷载组合后的设计竖向荷载以及初始水平侧向荷载施加到结构，后将等效水平地震荷载划分成若干个增量并逐次施加.在每个增量步中，假定刚度矩阵保持不变.且每步结束后，计算相应的刚性系数r，并代入式(1)得到下一增量步的结构刚度矩阵.每一步分析中，对各构件节点的塑性程度P进行评估，其表达式为

P=100×(1-r)%

(12)

FEMA-273将结构抗震性能目标水平定义为4个等级，即正常使用(Operational)、立即入住(Immediate occupancy)、生命安全(Life safety)和防止倒塌(Collapse prevention).以结构顶层位移值作为性能指标，取建筑结构高度的0.4%，0.7%，2.5%和5%分别作为OP，IO，LS和CP等级的最大侧向位移允许值.各性能等级状态下地震设计加速度的设置式[11]为

i=OP,IO,LS,CP

(13)

并计算各性能状态下的静力等效地震荷载Pi为

(14)

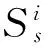
Pushover分析的等效地震荷载的加载模式采用指数分布形式，即

(15)

式中：Fs为作用在s层的等效水平地震荷载；Hs和Hn分别为s层和n层距离基础的高度；Gs和Gn分别为s层和n层地震设计质量；k为相关参数.

编制基于Matlab的Pushover的分析程序.图4为Pushover分析的基本流程，其中i为增量步数；Δu和Δf分别为位移和内力的增量.

2 试验设计

对图5中的两榀平面钢框架进行静力试验[12]，框架顶层左端作用不断增大的侧向水平荷载F，取顶层右端水平位移作为目标位移，记录并得到其荷载—位移曲线.框架荷载工况如表2所示，构件截面属性见表3.

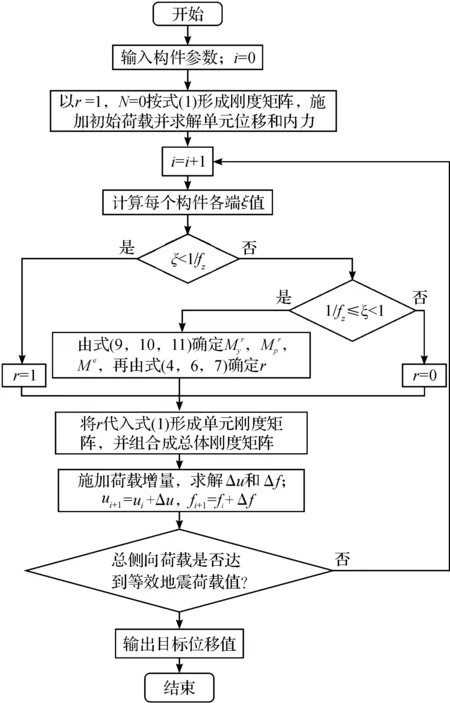
图4 Pushover分析基本流程Fig.4 Basic process of Pushover analysis

图5 框架几何模型Fig.5 Geometry model of frames

节点双层单跨/kNPxPy双层双跨/kNPxPy1F42F1420420303012

表3 截面构件属性

3 数值验证结果

为验证Pushover方法的可靠性和分析计算精度，将两榀框架的Pushover分析计算结果与其试验数据[12]进行了对比，对比结果如图6所示.

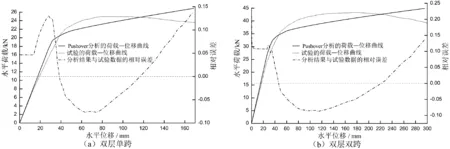
图6 Pushover分析结果与试验数据对比Fig.6 Comparison of result of Pushover analysis and test data

图6中两榀框架的Pushover分析与试验数据的对比结果可以看出：两榀钢框架的Pushover分析计算结果与试验数据较为接近.弹性变形阶段，两者图线吻合较好；随着塑性变形开展，两图线出现些许偏离后又交叉.整体上看，两图线走势基本相近.塑性发展末期，试验结果曲线更快趋平，而分析结果曲线则由于刚度矩阵设置的局限性仍存在小幅上倾趋势.且两榀框架计算分析结果与试验结果的最大相对误差分别为13.94%和12.17%.塑性变形开展的前中期，相比于试验结果，Pushover分析结果中的水平位移增长更快.这可能是由于Pushover分析模型考虑了节点的半刚性连接，而实际试验中构件节点因采用满焊连接，刚性较大因而位移较小.塑性变形末期，采用Pushover程序分析计算的水平位移略小于试验值，部分原因是分析程序的基本模型忽略了结构剪切变形的的影响.

对比结果表明：Pushover分析结果与试验数据的荷载—位移曲线基本吻合，两者相对误差小于14%.因此Pushover分析方法和程序可靠，可作为结构抗震性能分析工具，应用于基于性能的抗震设计中.

4 抗震分析算例

图7为文献[9]中一三层四跨半刚性连接的框架抗震分析算例.钢材弹性模量为200 GPa，框架梁、柱的屈服强度分别为339，397 MPa.结构自重及活荷载等效为竖向均布荷载作用于梁上，地震荷载的加载模式采用式(15)所示的指数分布模式，其中k=2.第一、二层的地震设计重量均为4 688 kN，顶层重量为5 071 kN.采用Pushover分析程序对该框架算例进行抗震分析，取中柱顶端的水平位移作为结构顶层位移.

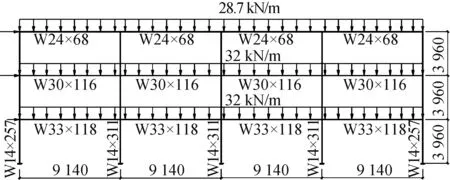
图7 三层四跨框架Fig.7 Four-bay three-story frame

表4给出了OP，IO，LS，CP这4个等级的性能目标水平状态下的结构顶层位移.Pushover分析程序所得的各性能等级下的顶层位移与文献[9]分析结果非常接近，两者偏差仅分别为0.67，1.31，2.28，0.24 cm.另外图8给出了Pushover程序分析所得的等效地震荷载—顶层位移曲线和文献[9]中分析所得曲线，可以看到两曲线基本吻合.

表4 各性能状态下的顶层位移

注：1) g为重力加速度.

图8 三层四跨框架的地震荷载—顶层位移曲线Fig.8 Seismic load-roof displacement curves of four-bay three-story frame

图9为框架各构件在4个等级的性能目标水平状态下的塑性发展状况.OP性能状态前，框架各构件均处于弹性阶段，荷载与顶层位移成线性关系.后随等效地震荷载的增大，顶层受力侧最近的梁的右节点先发生塑性变形，且最早出现塑性铰.IO性能状态之后塑性变形逐渐由顶层受力侧的梁向右侧和下侧的梁传递，结构位移不断加速增大.直到受力侧第2根柱和中柱柱底节点最先出现塑性变形，顶层位移迅速增大，荷载—位移曲线开始逐渐趋平.而后结构塑性程度不断增大，塑性铰也相继出现.LS到CP段的位移增量达到了弹性阶段总位移的7倍多.

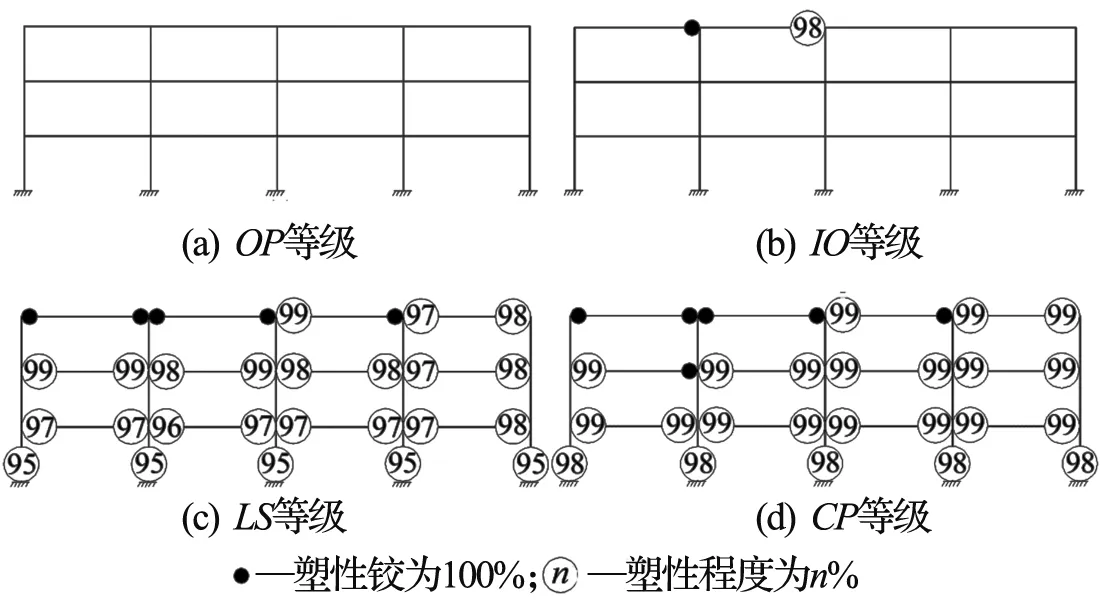
图9 各性能状态下的塑性状况Fig.9 Plastic behavior at different performance levels

5 结 论

以结构位移作为性能指标，论述了一种的非线性静力弹塑性Pushover分析方法用于结构抗震性能分析.通过对两榀框架分析与试验对比，显示了两者之间较好的契合度，表明了Pushover分析方法的可靠性.且通过一框架算例的抗震性能分析说明Pushover方法在抗震分析中的具体应用，显示了该方法的适用性，为基于性能的抗震设计提供了一种可靠的结构抗震性能分析工具.

[1] 李灿灿，陆洲导，李凌志.建筑结构基于性能的抗震设计[J].四川建筑科学研究，2005，31(5)：99-102.

[2] 张新军，徐江江，虞周均.斜拉-悬吊协作体系桥抗震性能参数分析[J].浙江工业大学学报，2014，42(6)：665-670.

[3] 曹亮，丁翠红，丁伯阳.杭州未设防高层建筑的抗震验算[J].浙江工业大学学报，2004，32(6)：656-659.

[4] 李辉，曹亮.在役结构的抗震计算分析[J].浙江工业大学学报，2005，33(2)：223-226.

[5] 高依强，陈永锋，李青宁.桥梁双柱式桥墩的Pushover分析[J].交通科技与经济，2014，16(4)：40-43.

[6] 潘毅，杨成，赵世春，等.基于Pushover方法的既有建筑结构安全性鉴定[J].西南交通大学学报，2010，45(2)：174-178.

[7] 张文明，高大峰，苏军，等.基于性能的框架结构抗震安全评估方法研究[J].西北地震学报，2007，29(4)：330-334.

[8] 刘畅，邹银生.多层偏心结构的Pushover分析[J].重庆建筑大学学报，2007，29(3)：61-65.

[9] HASAN R, XU L, GRIERSON D E. Push-over analysis for performance-based seismic design[J]. Computers and structures,2002,80(31):2483-2493.

[10] GONG Yangling. Performance-based design of steel building frameworks under seismic loading[D]. Waterloo: University of Waterloo,2003.

[11] Federal Emergency Management Agency. FEMA 273 NEHRP commentary on the guidelines for the rehabilitation of building[R]. Washington: Federal Emergency Management Agency,1996.

[12] 舒兴平，沈蒲生，尚守平.钢框架结构二阶弹塑性稳定极限承载力试验研究[J].钢结构，1999，14(4)：19-22.

(责任编辑：陈石平)

A Pushover analysis for performance-based seismic design

LI Peihao, LIU Chongqi

(College of Civil Engineering and Architecture, Zhejiang University of Technology, Hangzhou 310014, China)

An elasto-plastic Pushover analysis technique is presented for the performance-based seismic analysis by taking the top displacement as a performance index and a corresponding Matlab program is compiled. To validate the rationality and reliability of the technique, the program is used to analyze two plane steel frames: two-storey one-bay and two-storey two-bay, and the numerical results are compared with experimental data. It is shown that the computed load-displacement curve is in good agreement with experimental results with a relative error smaller than 14%. This indicates that the Pushover analysis technique and program are reliable. With the Pushover analysis as an analytical tool, the seismic analysis for a three-storey four-bay frame is made to show its applicability.

performance-based seismic design; Pushover analysis; steel frame

2015-12-08

国家自然科学基金资助项目(51008281)

李沛豪(1978—)，男，湖北黄冈人，副教授，博士，研究方向为计算结构力学与结构优化，E-mail: pumalph@163.com.

TU311.1

A

1006-4303(2016)05-0538-05