高超声速飞行器受热壁板的气动弹性声振分析
杨智春, 刘丽媛, 王晓晨
1.西北工业大学 航空学院, 西安 710072 2.北京航空航天大学 航空科学与工程学院, 北京 100083
高超声速飞行器受热壁板的气动弹性声振分析
杨智春1,*, 刘丽媛2, 王晓晨1
1.西北工业大学 航空学院, 西安 710072 2.北京航空航天大学 航空科学与工程学院, 北京 100083
高超声速飞行器壁板在非定常气动力、热载荷和噪声载荷构成的多物理场联合作用下,将表现出复杂的非线性气动弹性声振响应,特别是在颤振临界动压附近,受热载荷以及声载荷作用,壁板表现出复杂的跳变运动。基于von Karman大变形板理论,建立了热-声载荷和气动力共同作用下的壁板运动方程,分析了超声速气流中受热壁板的屈曲变形及热屈曲稳定性,借助势阱概念初步分析了壁板跳变运动产生的机理。通过定义“穿零频次”给出了跳变运动定量的分类方法,并计算得到不同温升和动压情况下,壁板发生跳变运动所对应的临界声压级。结果表明:在颤振临界动压之前,随着动压的增加,受热壁板势阱的深度先增大后减小,且受热壁板的势阱深度随着温升的增加而增大。
壁板; 气动弹性; 气动加热; 声振响应; 跳变; 热屈曲; 势阱
高超声速飞行往往伴随着非定常气动力、气动热和气动噪声联合作用带来的复杂环境,这对飞行器机体结构的设计和制造都提出了更高的要求。尤其是对于机体壁板结构,由于其自身的弹性变形受到结构几何非线性影响,在非定常流场、温度场和噪声场的联合作用下,壁板的运动将表现为复杂的非线性动力学响应[1]。特别是在考虑热、声载荷的作用后,壁板在亚临界颤振范围的振动响应不可忽视,壁板结构容易产生疲劳损伤,从而影响飞行器结构的疲劳寿命[2]。
近年来,国外许多学者开展了对超声速气流中壁板非线性气动弹性响应行为的研究。Mei等[3-4]在非线性von Karman结构模型和活塞理论气动力模型基础上建立了壁板颤振方程,分别在频域和时域内分析了壁板颤振稳定性和非线性颤振响应。Dhainaut等[5-7]运用模态降阶的有限元法研究了壁板在噪声激励下的颤振响应,发现噪声载荷在颤振临界点前后都起着明显的作用,并且热屈曲效应对壁板动力学响应的影响不可忽略。Miller等[8]将气动热-噪声环境下的壁板颤振系统分解为双向耦合的气动热系统和声气动弹性系统,在时域上采用不同步长递进更新两个子系统来进行求解。Sucheendran等[9]采用解析方法,对发动机进气道壁板在流场作用下的结构-声振耦合问题进行了研究。Ostoich等[10]采用数值方法进行了流固耦合仿真,研究了当壁板进入极限环状态时,壁板边界层与壁板结构的耦合效应,发现湍流的统计参数随着壁板的运动发生了改变。与此同时,还有许多学者开展了受热-噪声载荷作用的壁板动响应研究。Przekop等[11]研究了热声载荷下薄壁结构非线性振动响应,分析了跳变运动对金属薄壁结构热声疲劳寿命的影响。Mignolet和Soize[12]提出双模态降阶法,结合热传导模态方法分析了结构的噪声响应。
在国内,杨智春教授团队[1,13]开展了一系列超声速复合材料平壁板/曲壁板热颤振特性研究。杨超教授团队[14]开展了气动热-气动弹性双向耦合的高超声速曲面壁板颤振问题的研究,重点集中在曲壁板热屈曲前后的气动弹性行为。杨翊仁教授团队[15]重点研究了亚声速流中二维壁板在外激励作用下的复杂响应及分叉问题。沙云东教授团队[16-17]开展了热声载荷作用下壁板结构非线性响应特性的研究,并采用势阱的概念来解释跳变现象产生的机理。
从现有的文献看,目前对于高超声速气流中壁板动力学响应问题的研究,大多是只考虑热载荷及噪声载荷作用下的壁板强迫振动响应、或只考虑气动载荷及热载荷对壁板的联合作用,而考虑高超声速飞行器壁板实际上同时受到气动载荷、噪声载荷和热载荷作用的研究较少,探究壁板在颤振临界动压附近,由于热声载荷及气动载荷联合作用下出现的复杂动力学响应规律的更少。本文认为,研究高超声速气流中受热壁板在噪声载荷下的气动弹性响应问题,可以更加准确地预计高超声速飞行器壁板结构的振动响应特性,进而才能为壁板疲劳寿命研究提供基本数据。
本文建立了简支二维受热壁板的气动弹性声振模型,采用数值仿真方法求解不同动压和声载荷下壁板的气动弹性声振响应,研究了温度场、流场及远场限带高斯白噪声共同作用下壁板结构的气动弹性声振特性,针对文献[7]中的结论“噪声载荷在壁板颤振临界点前后都起着明显的作用,而且热屈曲效应对壁板动力学响应的影响不可忽略”,重点研究了壁板在颤振临界动压附近,由于热声载荷作用而出现的复杂跳变运动问题。通过定义“穿零频次”来研究跳变现象发生的规律并探索跳变现象产生的机理,计算得到不同温升和动压情况下壁板发生跳变运动所对应的临界声压级。不仅有助于加深对气动弹性声振机理的认识,同时也可为高超声速飞行器壁板抗疲劳设计提供依据。
1 理论分析

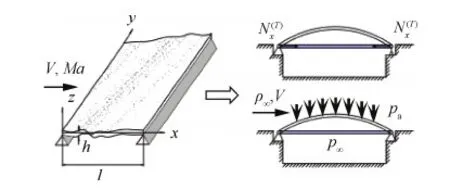
图1 两端简支二维受热壁板Fig.1 Simply supported two-dimensional heated panel
根据von Karman大变形板理论,在流场动压、温度载荷以及声载荷共同作用下,壁板的运动方程为[18]
ρh(∂2w/∂t2)+c(∂w/∂t)+D(∂4w/∂x4)-
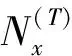
(1)
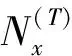

(2)
引入下列无量纲参数:
对两端简支平壁板,当λ=0系统达到渐进稳定的充要条件是温升值Rx<π2,Rx=π2对应的温升值为临界温升值ΔTcr[13],从而定义温升比为rx=ΔT/ΔTcr=Rx/π2,后面统一叫做温升。
对方程式(1)进行无量纲化,得到壁板运动的无量纲方程:

(3)
式中:ν为泊松比。
采用伽辽金方法,将位移函数展开成各阶谐波模态的叠加。设满足壁板简支边界条件的位移函数为
(4)
假设壁板变形主要由其前N阶模态组成,将式(4)代入到式(3)中,并进行傅里叶积分可以得到离散后的壁板运动的状态空间方程:
(5)
将受热壁板的状态空间运动方程写成矩阵形式,即
(6)
对于壁板颤振问题,已有的研究结果表明:对于一个二维各向同性的两端简支壁板,采用模态坐标法研究其颤振特性至少需要六阶模态[13]。然而,当壁板同时受到高频噪声载荷作用时,会激起更高阶的模态。选用铝合金壁板作为研究对象,其长度和厚度为l×h=254 mm×0.762 mm、弹性模量E=72.3 GPa、泊松比ν=0.3、密度ρ=2 750 kg/m3。当计算参数范围取在0≤λ≤800,0≤rx≤6,0 dB≤SPL≤140 dB(SPL为声压级),选用的模态阶数大于12时,壁板前缘3/4位置处的位移响应均方根值(Root Mean Square, RMS)随模态阶数的变化小于1%。图2给出了无量纲动压λ=800,rx=0,SPL=120 dB时壁板3/4弦向点处的振动响应(无量纲位移W和无量纲速度dW/dτ)随模态阶数的变化,可以看出,当模态阶数取为12时,壁板振动响应已经包含了主要模态的振动。

图2 壁板振动响应包含的主要模态Fig.2 Dominant modes in panel vibration response
采用四阶龙格-库塔数值积分法求解壁板气动弹性声振运动方程式(6),获得壁板结构的模态位移,然后再代回到位移函数式(4)中,即可得到壁板的时域位移响应。
2 跳变运动特性
目前,高超声速飞行器构型一般采用嵌入式推进系统、翼身融合和升力体布局,机体的壁板结构承受边界层扰动、推进系统及自身振动引起的高强噪声载荷激励(局部区域声压级可能超过180 dB)[19]。由于非定常气动载荷与受热壁板结构的耦合作用,特别是在颤振临界失稳动压附近,强烈的噪声载荷作用下,可使壁板结构产生复杂的动力学响应,薄壁结构往往产生跳变运动,由此导致的交变应力,会在壁板结构的材料缺陷处引发疲劳裂纹而引起结构疲劳失效[20]。
2.1 声振响应的穿零频次
目前对噪声激励下受热壁板的声振响应研究中,只是将声振响应进行定性的分类[16],还没有一个量化的方法对壁板声振响应进行分类。考虑到当壁板响应发生跳变时,壁板实际上是从一个屈曲后平衡位置跳跃到另一个屈曲后平衡位置,在这个过程中一定会穿越壁板的初始平衡位置即响应零点,同时发现声压级越大,穿越响应零点的次数也越大。因此,定义“穿零频次”来定量地描述跳变发生的频率:
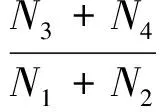
(7)

图3 受热壁板不同类型的气动弹性声振响应 Fig.3 Different types of aeroelastic vibro-acoustic response of heated panels
式中:N1、N2、N3和N4分别为在一段时域历程中峰值点、谷值点、由负位移穿越到正位移的点和由正位移穿越到负位移的点的个数。图3给出了壁板3/4弦向点处不同形式的无量纲位移W随无量纲时间τ变化时程图,借助上面定义的声振响应“穿零频次”,本文将受热壁板的气动弹性声振响应划分为以下5种运动形式:① 屈曲失稳,壁板最终稳定在某一个屈曲后平衡位置(图3(a));② 屈曲后,壁板围绕着一个屈曲后的平衡位置振动(图3(b));③ 屈曲后,壁板发生间歇的跳变运动(图3(c));④ 屈曲后,壁板在两个屈曲后平衡位置之间的频繁跳变运动(图3(d));⑤ 壁板随机振动 (图3(e))。
对本文算例研究的壁板,5种运动形式对应的“穿零频次”取值范围如表1所示。
表1运动形式与对应穿零频次的关系
Table1Relationshipbetweenmotionpatternandzero-crossfrequency

FrequencyrangeMotionpattern①Nf=0Staticbuckling②Nf=0Vibrationaboutapost⁃bucklinge⁃quilibriumpoint ③Nf∈(0,0.3)Intermittentsnap⁃throughmotion④Nf∈(0.3,0.5)Frequentsnap⁃throughmotion⑤Nf∈(0.5,1.0)Randomvibration
2.2 热声载荷作用下壁板的跳变运动规律
为了探究声载荷作用下受热壁板气动弹性声振响应的跳变规律,计算得到不同动压、温升和声压级下声振响应的“穿零频次”。结果表明:动压不变,随着温升系数rx的增加,穿零频次值减小;温升不变,在动压超过壁板颤振失稳临界动压后,随着动压的增加,跳变的“穿零频次”也增加。由前文的定义,临界热屈曲无量纲温升系数rx=1,且当无量纲动压λ>200时,振动的形式主要是随机振动。因此,后续讨论的参数范围将集中在2≤rx≤6,0≤λ≤150范围内,重点关注颤振失稳临界动压附近的壁板振动。后文提到的动压均为无量纲的动压值。
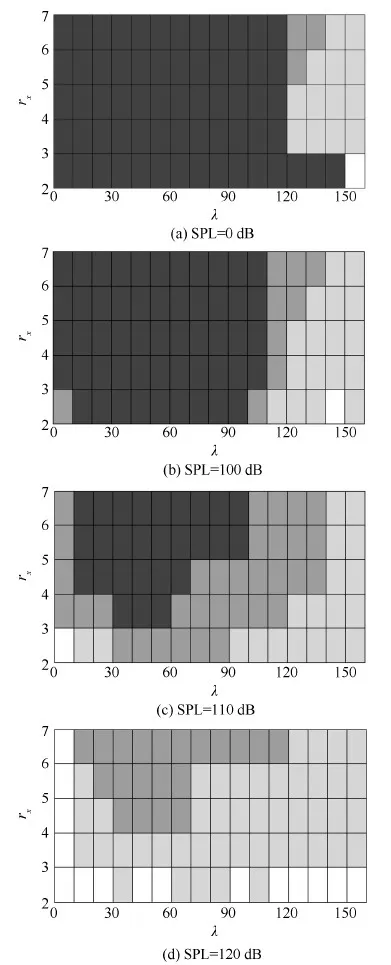
图4 不同声压级下跳变情况分布图Fig.4 Snap-through motions distribution under different acoustic pressure levels
图4给出了声压级SPL=0,100,110,120 dB的跳变情况分布图。灰度由深到浅依次对应无跳变、间歇跳变、频繁跳变和随机振动。从图4(a)中可以看到,即使没有声载荷作用,壁板也会产生跳变运动;结合图4(a)和图4(b)可以看到,当SPL≤100 dB时,跳变运动主要集中在颤振临界动压附近(λ=109.6);图4(c)中,当2≤rx≤6时,在所考察的动压范围内,动压取两端的值时,壁板会发生间歇跳变,动压取中间的值时,壁板围绕着某一屈曲后平衡位置作随机振动,且随着rx的增加,具有Nf=0的参数取值范围会变得越来越宽;由图4(c)和图4(d)均能明显看出,随着动压的增加,跳变穿零频次呈先减小后增加的趋势,从图4(d)中可以看到,当SPL≥120 dB之后,在所考察的动压与温升范围内,壁板不存在围绕某一屈曲后平衡位置振动的情况。
2.3 声载荷作用下的跳变运动机理
沙云东教授在研究热声载荷作用下薄壁结构的非线性响应特性时,引入了势阱的概念来解释壁板跳变运动产生的机理[16]。所谓势阱,是指当动力学系统的势能函数曲线随某一参数变化,而在参数空间的某一范围内具有最小值,势能曲线呈陷阱状这一现象。基于这个概念,对文献[16]的简化壁板结构单自由度模型势能表达式进行无量纲化,就得到无量纲势能表达式U=π4(1-rx)a2/2U=π4(1-rx)W2/2+6(1-ν2)π4a4/8+3(1-ν2)π4W4/4,由壁板无量纲势能表达式可以得到单自由度壁板模型在不同温升下的势能U随无量纲位移W的变化曲线,如图5所示。从图5中可以看出,当rx≤1时,势能曲线呈现单凹形状(势阱),平板在原点处势能最小,对应初始平衡位置。当rx>1时,平板处于屈曲后区域,具有两个势能最低点,对应两个屈曲后平衡位置,而初始平衡位置转变为不稳定平衡位置。随着温升系数rx的增加,屈曲后平衡位置的变形绝对值增大,势阱也随之加深。

图5 单自由度(SDOF)壁板系统在不同温升下的势能曲线 Fig.5 Potential energy curves of single degree of freedom (SDOF) panel system under different temperature elevation ratio
为了验证本文所用计算程序正确,采用数值模拟方法求解了在不考虑气动力作用下屈曲后平衡位置,并与应用势阱概念得到的理论结果进行对比,如表2所示。可以看出,数值模拟结果WS与理论结果WT误差均在3%左右,验证了所用计算程序对模拟壁板结构声振响应的准确性。
表2屈曲后平衡位置计算结果WS与理论结果WT对比(无量纲位移)
Table2ComparisonbetweensimulatedresultsWSandtheoreticalresultsWTofpost-bucklingequilibriumposition(non-dimensionaldisplacement)
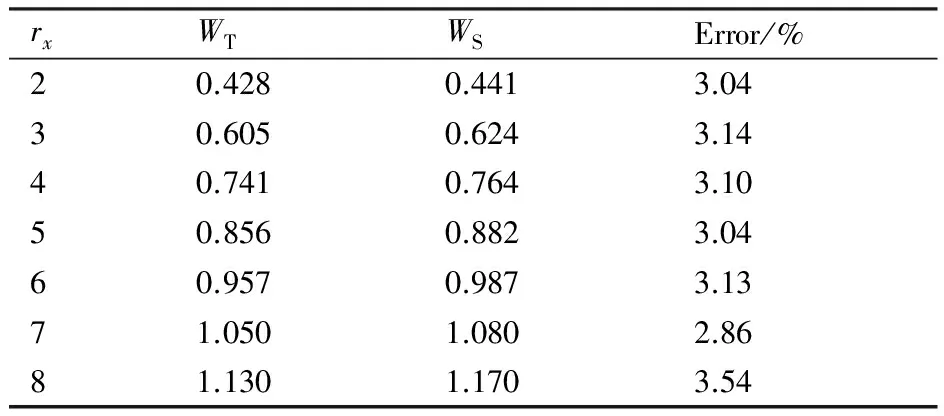
rxWTWSError/%20.4280.4413.0430.6050.6243.1440.7410.7643.1050.8560.8823.0460.9570.9873.1371.0501.0802.8681.1301.1703.54
显然,势阱越深,受到相同的声载荷激励,壁板发生跳变的可能性越小。文献[16]已经证明了温升会影响仅受声载荷的壁板的势阱深度,本文将考察受热壁板气动弹性声振系统中,动压和温升是如何影响势阱的深度。
为了探究声载荷作用下受热壁板气动弹性系统的跳变机理,必须先求解受热壁板气动弹性系统对应静态方程的非零解。为此,令式(5)中所有状态变量对时间的导数项全都等于零,得到
[(sπ)4-Rx(sπ)2]as+6(1-ν)2·
s=1,2,…,N
(8)
写成矩阵形式,即
(KL-RxKR+λKA+KNL)·a=0
(9)
式中:KL为线性弹性刚度矩阵;KR为热应力引起的刚度矩阵;KA为气动刚度矩阵;KNL为非线性弹性刚度矩阵。其表达式分别为
当来流速压较低时,热应力是导致壁板变形的主要因素,因此,采用二阶谐波模型来分析受热壁板的热屈曲稳定性[13],热壁板的静态方程式(8)可简化为
(10)
中间变量:
一阶模态位移a1和二阶模态位移a2有非零解的充要条件为

(11)
要H为实数,则必须有λ≤9π4/8≈109.6,当来流速压超过该边界,则a1和a2不存在非零解,即壁板不可能稳定在静态屈曲变形状态,λ=109.6为颤振临界动压。
采用牛顿迭代法求解方程式(9),为了扩大迭代收敛的初始范围,选用牛顿下山法,得到屈曲后平衡位置。同时,解析求解简化后受热壁板的静态方程式(10),得到屈曲后平衡位置。如图6所示,两种方法得到的屈曲后平衡位置的变化趋势一致,求解二阶谐波模型得到的计算结果略微偏小。
图6给出了不同温升情况下,无量纲的屈曲后平衡位置W随无量纲动压λ的变化情况。从图中可以看出,固定动压λ,随着温升rx的增加,屈曲后平衡位置增大,这与前面的结论相吻合;固定温升rx,随着动压λ的增加,屈曲后平衡位置先增大后减小。这恰好可以解释图4中出现的在λ区间的两端会发生间歇跳变,在λ区间的中间范围不发生跳变的现象。

图6 不同温升下屈曲后平衡位置随动压的变化情况Fig.6 Change of post-buckling equilibrium position with dynamic pressure under different temperature elevation ratio
2.4 跳变运动对应的临界声压级
当rx>1,在不考虑壁板所受声载荷时,动压达到颤振临界动压之前,壁板结构受扰动后,最终稳定在屈曲后平衡位置,动压超过颤振临界动压后,壁板结构发生混沌颤振[13]。在考虑壁板受到声载荷作用,动压小于颤振临界动压时,随着声压级的增加,会依次出现图3中的5种运动形式。定义壁板的运动形式从屈曲后绕某一平衡位置振动,变化到屈曲后间歇跳变运动所对应的声压级为失稳前跳变临界声压级。表3给出了动压小于颤振临界动压时,不同温升比和动压对应的失稳前跳变临界声压级SPLcr。从表3中可以看出,失稳前跳变临界声压级随温升的增加而增大,随动压的增加先增大后减小,这样的规律与图4中所显示的规律一致。当SPL≥120 dB,在所研究的动压和温升范围内,壁板结构均发生了跳变运动。当SPL≤100 dB,壁板结构均不发生跳变运动。
表3屈曲前不同温升和动压下对应的临界声压级(SPLcr)
Table3Criticalacousticpressurelevel(SPLcr)underdifferenttemperatureriseanddynamicpressurebeforebuckling

λSPLcr/dBrx=2rx=3rx=4rx=5rx=6010510511011011010105110110110115201101101151151203010511011011512040105110110120115501051101101151206011011011011011570105110110110115801051101101101109010011011011011010095105110110110110No100105105105
当不考虑声载荷作用时,当动压超过颤振临界动压后,壁板结构出现混沌颤振。表4给出了λ=120,rx=5情况下,壁板位移响应均方根值Wrms和穿零跳变频次随声压级的变化。从表4中可以看出,随着声压级的增加,壁板位移均方根值和穿零频次逐渐增加,直到声压级增加到某一临界声压级后,穿零频次会突然增加,壁板的运动形式将从屈曲后间歇跳变运动变为屈曲后频繁跳变运动。将此刻对应的声压级定义为失稳后跳变临界声压级。表5给出了动压分别为110和120时对应失稳前、后的跳变临界声压值,在相同的温升条件下,失稳后跳变临界声压级要大于失稳前跳变临界声压级,*为在对应的动压和温升条件下,运动形式为随机振动。
表4无量纲位移均方根值Wrms和穿零频次Nf随声压级的变化
Table4VariationofRMSvalueWrmsofnon-dimensionaldisplacementandzero-crossfrequencyNfwithdifferentacousticpressurelevels

SPL/dB90110115120Wrms0.78050.81910.81450.9147Nf0.17920.19220.19740.3869
表5失稳前后壁板临界声压级比较
Table5Comparisonofcriticalacousticpressurelevelofpanelbeforeandafterinstability

λSPLcr/dBrx=2rx=3rx=4rx=5rx=6110∗100105105105120∗∗115120125
2.5 考虑气动力作用下的跳变特点
作用在壁板上的气动力不仅会影响壁板系统是否会发生跳变,同时也会改变系统跳变运动的形式。图7给出了λ=110,rx=5,SPL=110 dB情况下受热壁板气动弹性声振系统的跳变运动,从响应的时间历程以及相图可以看出,与无气流作用的壁板结构声振响应类似,壁板在围绕着两个屈曲后平衡位置振动的同时,也在两个平衡后位置之间不断跳变。由图7(a)可以看出,高超声速气流中的壁板结构跳变运动呈现出以下特点:① 跳变运动具有拟周期性;② 从一个屈曲后平衡位置跳变到另一个平衡位置后,绕平衡位置作衰减振荡;③ 即将发生跳变前,振动已经偏离该平衡位置而趋向另一个平衡位置。
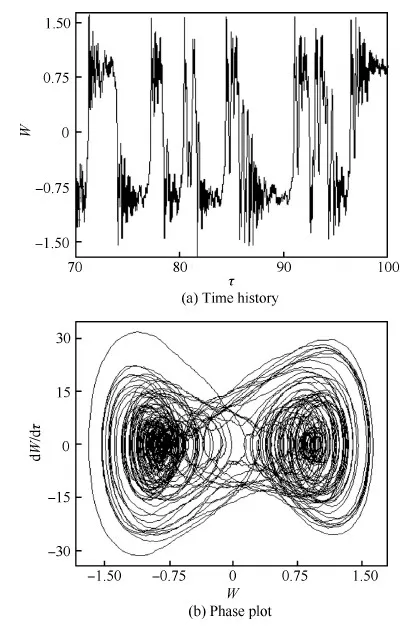
图7 声载荷作用下受热壁板气动弹性系统的跳变运动(SPL=100 dB,λ=110,rx=5)Fig.7 Snap-through response of heated panel aeroelastic system subjected to acoustic load (SPL=100 dB,λ=110,rx=5)
上面提到的3个现象只有当温升较大且动压在颤振临界动压附近时才会明显表现。较大的温升增加了系统的势阱深度,围绕屈曲后平衡位置振动的幅度因此也比较大。跳变运动在屈曲后平衡位置的振动呈现收敛的趋势,而颤振临界动压恰恰是壁板静态屈曲失稳的边界,在小于颤振临界动压时,振动形式表现为收敛的屈曲失稳。
3 结 论
1) 受热壁板声振响应跳变的“穿零频次”和屈曲后平衡位置均随温升的增大而减小,在颤振临界动压之前,随着动压的增大先增大后减小。屈曲后平衡位置与系统的势阱深度正相关,温升和动压之所以会改变跳变发生的“穿零频次”,是因为其改变了壁板系统的势阱深度。
2) 对于屈曲后壁板,在动压超过颤振临界动压之前,随着声压级的增大,壁板的运动形式由屈曲后绕某一平衡位置的随机振动,变为屈曲后的间歇跳变运动,对应的跳变临界声压级为失稳前临界声压级。在动压超过颤振临界动压之后,随着声压级的增大,壁板的运动形式由屈曲后的间歇跳变运动,突然变为屈曲后的频繁跳变运动,对应的跳变临界声压级为失稳后临界声压级。颤振失稳后的跳变临界声压级大于失稳前的跳变临界声压级。
3) 在颤振临界动压之前,当声压级在100 dB以下,壁板不会发生跳变,当声压级超过120 dB,几乎在所有动压和温升情况下壁板都会发生跳变运动。
[1] 杨智春, 夏巍. 壁板颤振的分析模型、数值求解方法和研究进展[J]. 力学进展, 2010, 40(1): 81-98.
YANG Z C, XIA W. Analytical models, numerical solutions and advances in the study of panel flutter[J]. Advances in Mechanics, 2010, 40(1): 81-98 (in Chinese).
[2] THIODOR H B, PAUL H. High speed research program sonic fatigue summary report: NASA/CR-2005-213742[R]. Washington, D.C.: NASA, 2005.
[3] MEI C. Large deflection multimode response of clamped rectangular panels to acoustic excitation: AFWAL-TR-83-3121[R]. [s.l.]: AF Wright Aeronautical Laboratories, 1983.
[4] ABDEL-MOTAGALY K, DUAN B, MEI C. Nonlinear response of composite panels under combined acoustic excitation and aerodynamic pressure[J]. AIAA Journal, 2000, 38(9): 1534-1542.
[5] DHAINAUT J M, GOU X, MEI C, et al. Nonlinear random response of panels in an elevated thermal-acoustic environment[J]. Journal of Aircraft, 2004, 40(4): 683-691.
[6] DHAINAUT J M, CHENG G F, MEI C. Response of plats under uniform random loads unsynchronized in time: AIAA-2006-1927[R]. Reston: AIAA, 2006.
[7] DHAINAUT J M. Nonlinear finite element modal formulation for panel flutter with thermal effects and acoustic excitation: AIAA-2012-1789[R]. Reston: AIAA, 2012.
[8] MILLER B A, MCNAMARA J J, SPOTTSWOOD S M, et al. The impact of flow induced loads on snap-through behavior of acoustically excited thermally buckled panels[J]. Journal of Sound and Vibration, 2011, 330(23): 5736-5752.
[9] SUCHEENDRAN M M, BODONY D J, GEUBELLE P H. Coupled structural-acoustic response of a duct-mounted elastic plate with grazing flow[J]. AIAA Journal, 2014, 52(1): 178-194.
[10] OSTOICH C M, BODONY D J, GEUBEUE P H. Interaction of a Mach 2.25 turbulent boundary layer with a fluttering panel using direct numerical simulation[J]. Physics of Fluid, 2013, 25(11): 110806.
[11] PRZEKOP A, RIZZI S A, SWEITZER K A. An investigation of high-cycle fatigue models for metallic structures exhibiting snap-through response[J]. International Journal of Fatigue, 2008, 30(9): 1579-1598.
[12] MIGNOLET M P, SOIZE C. Stochastic reduced order models for uncertain geometrically nonlinear dynamical systems[J]. Computer Method in Applied Mechanics and Engineering, 2008, 197(45-48): 3951-3963.
[13] 夏巍. 超音速气流中受热复合材料壁板的非线性颤振特性研究[D]. 西安: 西北工业大学, 2008.
XIA W. Nonlinear flutter of heated composite panels in supersonic airflow[D]. Xi’an: Northwestern Polytechnical University, 2008 (in Chinese).
[14] YANG C, LI G S, WAN Z Q. Aerothermal aeroelastic two-way coupling method for hypersonic curved panel flutter[J]. Science China Technological Sciences, 2012, 55(3): 831-840.
[15] 李鹏, 杨翊仁, 鲁丽. 外激励作用下亚音速二维壁板的复杂响应研究[J]. 计算力学学报, 2011, 28(6): 864-871.
LI P, YANG Y R, LU L. Complicated response analysis of two-dimensional thin panel in subsonic flow with external excitation[J]. Chinese Journal of Computational Mechanics, 2011, 28(6): 864-871 (in Chinese).
[16] 沙云东, 魏静, 高志军, 等. 热声载荷作用下薄壁结构的非线性响应特性[J]. 航空学报, 2013, 34(6): 1336-1346.
SHA Y D, WEI J, GAO Z J, et al. Nonlinear response characteristics of thin-walled structures under thermos-acoustic loadings[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1336-1346 (in Chinese).
[17] 沙云东, 郭小鹏, 廖连芳, 等. 随机声载荷作用下的复合薄壁结构Von Mises应力概率分布研究[J]. 振动与冲击, 2011, 30(1): 137-141.
SHA Y D, GUO X P, LIAO L F, et al. Probability distribution of Von Mises stress for complex thin-walled structures undergoing random acoustic loadings[J]. Journal of Vibration and Shock, 2011, 30(1): 137-141 (in Chinese).
[18] DOWELL E H. Nonlinear oscillations of a fluttering plate II[J]. AIAA Journal, 1967, 5(10): 1856-1862.
[19] BLEVINS R D, BOFILIOS D, HOLEHOUSE I, et al. Thermo-vibro-acoustic loads and fatigue of hypersonic flight vehicle structure: AFRL-RB-WP-TR-2009-3139[R]. Chula Vista, CA: Goodrich Aerostructures Group, 2009.
[20] 贺尔铭, 刘峰, 胡亚琪, 等. 热声载荷下薄壁结构非线性振动响应分析及疲劳寿命预测[J]. 振动与冲击, 2013, 32(24): 135-139.
HE E M, LIU F, HU Y Q, et al. Nonlinear vibration response analysis and fatigue life prediction of a thin-walled structure under thermal-acoustic loading[J]. Journal of Vibration and Shock, 2013, 32(24): 135-139 (in Chinese).
Analysisofaeroelasticvibro-acousticresponseforheatedpanelofhypersonicvehicle
YANGZhichun1,*,LIULiyuan2,WANGXiaochen1
1.SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100083,China
Hypersonicvehiclepanelincombinationwithunsteadyaerodynamicpressure,thermalloadingandacousticloadingexhibitsacomplexnonlinearaeroelasticvibrationresponse.Thepanelshowsacomplexsnap-throughresponse,especiallyinthevicinityofthecriticalflutterdynamicpressure.BasedonvonKarmanlargedeformationplatetheory,theequationsofmotionundertheinteractionofaerodynamicpressureandthermal-acousticloadingareestablished.Inaddition,thebucklingdeformationandthermalbucklinginstabilityofaheatedpanelinsupersonicflowisanalyzed.Accordingtothepotentialwelltheory,themechanismofsnap-throughphenomenonisexplored.Bydefiningzero-crossfrequency,aquantitativeclassificationmethodforsnap-throughmotionisproposed.Furthermore,thecriticalsoundpressurelevelunderdifferentdynamicpressureandtemperatureconditionsiscalculated.Theresultsshowthatwhenthedynamicpressureissmallerthanthecriticalflutterdynamicpressure,thedepthofthepotentialwellfirstincreasesandthendecreaseswithdynamicpressureincreasing.Andthedepthofpotentialwellincreaseswiththeincreaseoftemperaturerise.
panel;aeroelasticity;aerodynamicheating;vibro-acousticresponse;snap-through;thermalbuckling;potentialwell
2016-01-07;Revised2016-01-31;Accepted2016-04-03;Publishedonline2016-04-201526
URL:www.cnki.net/KCMS/detail/11.1929.V.20160420.1526.002.html
NationalNaturalScienceFoundationofChina(11472216)
2016-01-07;退修日期2016-01-31;录用日期2016-04-03; < class="emphasis_bold">网络出版时间
时间:2016-04-201526
www.cnki.net/KCMS/detail/11.1929.V.20160420.1526.002.html
国家自然科学基金 (11472216)
*
.Tel.:029-88460461E-mailyangzc@nwpu.edu.cn
杨智春, 刘丽媛, 王晓晨. 高超声速飞行器受热壁板的气动弹性声振分析J. 航空学报,2016,37(12):3578-3587.YANGZC,LIULY,WANGXC.Analysisofaeroelasticvibro-acousticresponseforheatedpanelofhypersonicvehicleJ.ActaAeronauticaetAstronauticaSinica,2016,37(12):3578-3587.
http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn
10.7527/S1000-6893.2016.0115
V211.47; O354.4
A
1000-6893(2016)12-3578-10
杨智春男, 博士, 教授, 博士生导师。主要研究方向: 飞行器气动弹性力学、 飞行器结构动力学与飞行器结构健康监测。Tel: 029-88460461E-mail: yangzc@nwpu.edu.cn
刘丽媛女, 硕士研究生。主要研究方向: 流固耦合与湍流模拟。E-mail: nwpu_candice@126.com
王晓晨男, 博士研究生。主要研究方向: 噪声振动与流固耦合。Tel: 029-88460461E-mail: wxc_npu@163.com
*Correspondingauthor.Tel.:029-88460461E-mailyangzc@nwpu.edu.cn

