无线传感网络节点隶属度模糊定位算法研究
李 锋
(广东交通职业技术学院,广州 510650)
无线传感网络节点隶属度模糊定位算法研究
李 锋
(广东交通职业技术学院,广州 510650)
无线传感网络RSSI算法理论上定位精度很高,但在实际工程应用中易受环境干扰和信号波动影响,无法精确,定位稳定性不好,误差较大,若穷追所有细节将极大增加算法复杂度;针对其中不足,提出基于节点隶属度模糊算法,并应用于RSSI定位模型之中;新算法首先利用岭形分布对RSSI初始信号模糊化取得隶属函数,再根据隶属度近似程度反馈求精,通过隶属程度以逐渐逼近方式定位节点坐标区域;新算法模糊化系数m值越大,抗干扰能力越强,但节点具有更多的相同或相似格贴近度,无法反映节点真实状态,因此m值应根据路径衰减指数和环境干扰物理值共同决定;通过仿真实验结果证明,与RSSI和DV-Hop算法相比,新算法可以减少环境干扰和信号波动带来的影响,具有更高的定位精度和稳定性。
无线传感器网络;隶属度;模糊算法;RSSI
0 引言
无线传感网络RSSI定位算法在实际工程应用中易受环境干扰和信号波动影响,无法精确,定位稳定性不好,误差较大,若穷追所有细节将极大增加算法复杂度[1]。如何减少环境干扰和信号波动带来的影响,提高定位精度和稳定性是近年研究的重点和难点。
1 WSN定位算法综述
无线传感节点定位算法分为无需测距算法和基于测距算法两类[2]。无需测距算法通过交换邻居节点连通状态信息,利用几何拓扑方法完成定位过程,代表算法有基于跳数的DV-Hop定位算法、基于三角测距的APIT算法和基于多维标度的MDS-MAP等算法[3]。无需测距算法信息收集过程简单,稳定性好,但定位精度较差,适用于小范围内节点密度较大,精度要求不高的场合。基于测距算法是通过测量节点间距离、时延、角度、强度等信息,从而计算节点坐标,代表算法有基于抵达时间的TAO算法、基于抵达角度的AOA算法和基于接受信号强度的RSSI等算法。测距算法理论上定位精度很高,但算法复杂,易受环境干扰和信号波动影响,定位稳定性不好[4-5]。
针对测距算法不足,提出基于节点隶属度模糊算法,并应用于RSSI定位模型之中。新算法首先利用岭形分布对RSSI信号模糊化取得隶属函数,再根据其近似程度反馈求精,通过隶属程度以逐渐逼近方式计算节点坐标区域。新算法可以减少环境干扰和信号波动带来的影响,具有更高的定位精度和稳定性。
2 RSSI测距算法
RSSI测距算法首先根据公式(1)建立信号传播损耗模型。
(1)
其中:RSSI (d)为距离源节点d处接收到的信号强度,RSSI (d0)为距离d0处测到的信号强度值,β为路径衰减指数,其值与具体环境和障碍物相关,Xδ为标准偏差为δ的正态随机变量。
对多个信号源建立传播损耗模型后,网络中每节点对应的信道多径衰减特征都是惟一的,形象的称为信号指纹。RSSI通过迭代求精,依据损耗模型将信号指纹信息转化为距离参数,利用三边定位法以求解方程组形式计算节点坐标,见图1。
(2)

图1 三边定位法
然而在实际部署中β衰减指数易受环境变化和信号波动影响,其值动态变化且难以预测,导致定位算法对环境依赖程度很大,适应性不强,定位结果不稳定。
3 模糊属性
在经典集合论中给定集合A,某一元素X要么属于A,要么不属于A。而模糊算法研究的对象没有明确界限,界限越模糊,集合的模糊程度也越高,集合中的元素并不是严格的“非此即彼”,也可能是“亦此亦彼”,只是对于不同集合隶属程度不同而己,称为隶属度[6]。
对于集合A,X为某一定义域上的全集,该全集上的模糊子集定义为:
(3)
其中,μA(x)称为x对于模糊子集的隶属度,μA为模糊子集A的隶属函数。
在隶属函数中,精确数可以转变为模糊数,模糊数也可以转变为精确数,通常采取最大隶属度、加权判定和岭形分布等方法[7]。
4 基于节点隶属度模糊算法
RSSI算法接受信号强度容易受环境干扰和信号波动影响,这些外界变量飘忽不定,无法精确,若穷追所有细节将极大增加算法复杂度。新算法将定量分析通过模糊算法转化为定性分析,将RSSI信号模糊化后通过隶属程度以逐渐逼近方式计算节点坐标区域,具体过程如下。
4.1 模糊度处理过程
考虑环境影响和信号波动导致的定位偏差,新算法利用隶属函数对RSSI初始信号模糊化,具体过程如下:
①设U为论域,则论域U中一个模糊集合A的隶属度μA(u) 为:

(4)
其中μA是隶属函数,其大小反映论域U中元素u相对于模糊集合A的隶属程度,值越接近1,隶属于集合A的程度越高。
②设模糊集合A∈f(U),∀λ∈[0,1],则集合A中λ的截集定义为:
(5)
③设模糊集合B∈f(U),则集合A和集合B内积、外积和格贴近度分别为:
A◎B =∨u∈U(A(u)∧B(u))
(6)
A⊙B=∧u∈U(A(u)∨B(u))
(7)
(8)
其中格贴近度表示模糊集合A和B之间的接近程度。
④定义模糊化区域fuzzy,包含对RSSI初始信号模糊化区域上限和下限,设信号模糊化指纹合集为rank,其中距离为i的rank为ranki,见图2。

图2 ranki模糊化区域
⑤利用岭形分布对RSSI信号模糊化,则ranki隶属函数表示如下:
(9)
模糊化隶属度岭形分布图见图3。
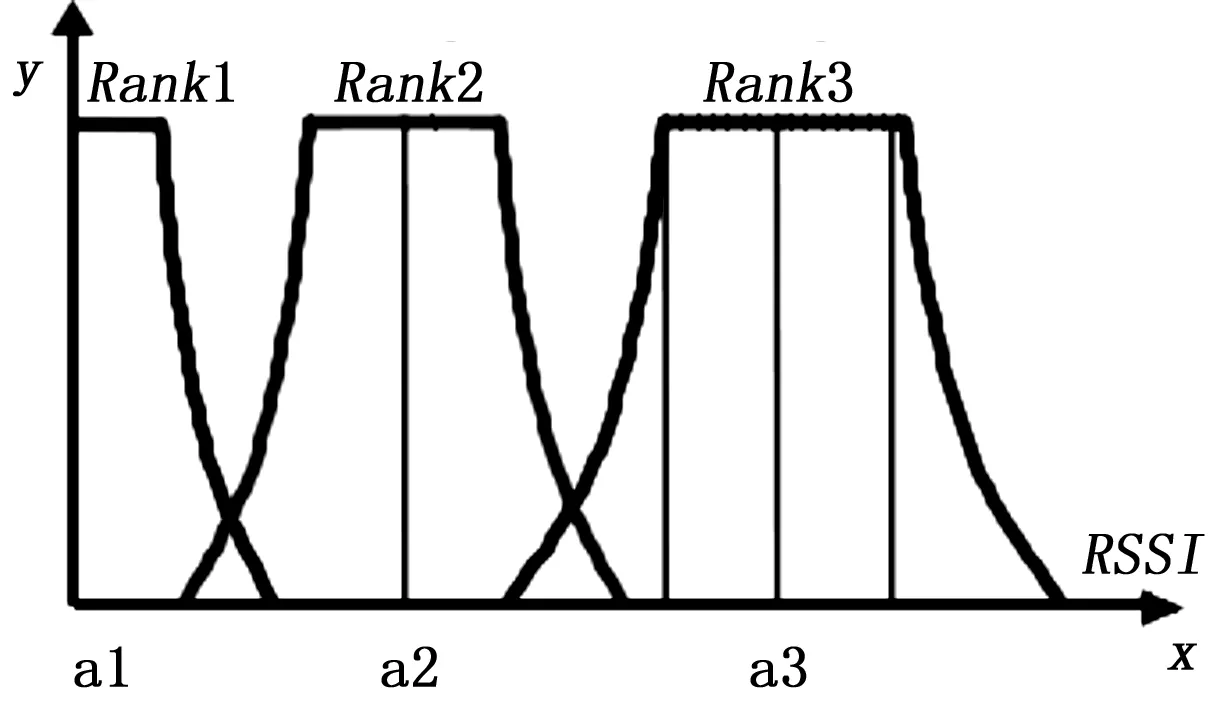
图3 隶属度岭形分布图
⑥根据公式(7)得出RSSI模糊隶属度向量:
v(rank1,rank2…,rankm)|=(μ1,μ2,…μm)
(10)
其中v是RSSI隶属于ranki的隶属度,参数m∈[0,1]反映模糊化程度。m值是模糊化程度,m值越小,生成的模糊集数量越少,模糊集ranki格贴近度也越小,此时算法抗干扰能力越弱,越接近标准RSSI测距算法;反之m值越大,生成的模糊集数量越多,模糊化后具备相同或相似的模糊隶属度向量值越多,抗干扰能力越强。
但是模糊程度m值并不是越大越好,当m趋于1时,算法虽不受环境干扰影响,但网络中所有节点向量经模糊化后都具备相同或相似的格贴近度,无法反映节点真实状态,如同DV-Hop算法中简单的将跳数作为衡量节点距离参数,跳数虽不受环境影响,但无法反映真实距离,在节点分布不均匀时将导致较大测距误差。因此m值大小应根据路径衰减指数β和环境干扰物理值共同决定。
4.2 迭代求精定位过程
对RSSI初始信号模糊化后,新算法根据RSSI信号指纹模糊近似度作出评价和反馈,并以此匹配求精计算节点坐标。因此模糊近似度必须能够对节点定位结果做出评价并进行迭代求精,具体过程如下:
①定义ranki的模糊特征向量ui=(ui1, ui2,…, uim),则ui与uj近似度rij为:
(11)
式(11)说明,当rij值趋于0时模糊向量差异最大,反之当rij值趋于1时,模糊向量趋于相同。
②设定位节点p (xp,yp)周围有k个邻居节点,则节点p模糊化后有k个模糊隶属度向量。设邻居节点q模糊隶属度向量为vq,节点p接收来自节点q的坐标和评价值分别为(xα,yα)和ω(q),则新算法对节点p模糊特征评价为:
(12)
其中rpq为模糊隶属度向量vα和节点p欧式距离d=‖(xp,yp), (xα,yα)‖之间的模糊匹配关系。
③将欧式距离d带入式(9)RSSI模糊化过程,得出元素数目为num(rank)的糊隶属度向量vd和近似度rpq的关系如下:
(13)
其中υq(i)和υd(i)是模糊隶属度向量中的第i个元素。
④新算法选取RSSI信号隶属度最大的几个rank进行比较,通过匹配rij和rpq的近似度反馈求精,在邻居节点中以逐渐逼近方式找出定位节点坐标区域,见图4。
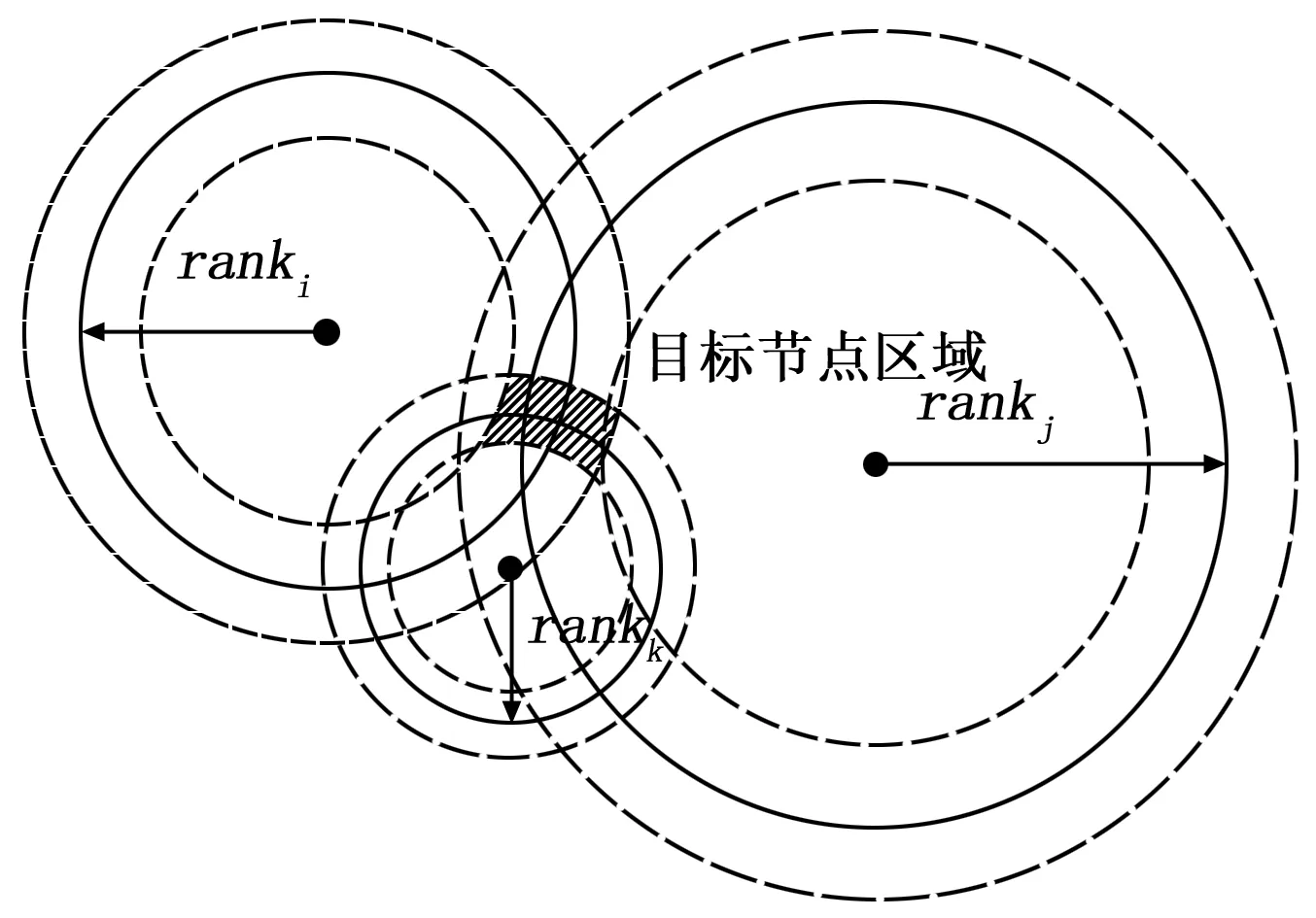
图4 模糊定位结果
5 仿真测试
5.1 测试环境
仿真环境设为500×500二维区域,节点通信半径为20 m,信号衰减使用RADAR模型,见公式(1),取β路径衰减指数为2.5。
5.2 定位偏差测试
选取60个节点均匀部署在二维区域中,并添加随机信号扰动系数DOI取值为0.25,初始化模糊参数m=0.85,共测试10次并取平均定位偏差,评价公式为:
(14)
仿真结果见图5。如图所示,3种算法测距偏差都随节点距离增加而加大,其中基于测距的RSSI算法起伏最大,受环境影响最为严重,无需测距DV-Hop算法基于跳数衡量节点之间距离,状态信息受环境影响较小,算法起伏不大,兼之节点均匀分布,测距误差小于RSSI算法;而新算法起伏最小,说明测距信息模糊化能有效减少环境干扰和信号波动带来的影响,定位偏差在3种算法中最小。

图5 3种算法定位偏差测试
5.3 抗干扰测试
重新选取60个节点随机部署在二维区域中,不断加大DOI系数以增强信号扰动幅度,初始化模糊参数m取值范围[0.55, 0.85],仿真结果见图6。在信号干扰为0时,标准RSSI算法和新算法偏差几乎相同,而DV-Hop算法定位偏差略大;随着信号干扰增强,RSSI算法定位偏差增大明显,起伏较大,定位结果不稳定,在DOI取值接近1时偏差距离几乎为新算法两倍,RSSI算法受环境影响严重;而DV-Hop算法受环境干扰影响较小,起伏相对平稳。但受节点非均匀分布影响,跳数无法真实反映节点真实距离,平均定位偏差接近RSSI算法,若进一步降低节点密集度,偏差将会进一步增大;新算法模糊系数m随扰动系数DOI取值而线性增大以减少环境影响,定位偏差起伏不大,充分发挥了测距算法定位精准的优势。

图6 3种算法抗干扰测试
5.4 新算法对移动节点的定位精度

图7 移动节点定位图
选取60个节点均匀部署在二维区域,随机初始化节点移动速度,测试结果见图7所示,其中圆圈表示节点物理位置,星号表示估算位置,横线越长,表示节点速度越大。新算法在保持抽样概率不变的情况下,节点移动速度越快,信号模糊化区域越广,以逐渐逼近方式找出移动节点坐标范围也随之增大,从而造成定位偏差。但由于节点均匀部署,每个节点能够从邻居节点隶属度值对定位结果作出评价并动态反馈,以此抵消节点因移动速度过快导致定位精度下降的问题。
6 结束语
RSSI算法定位精度很高,但没有考虑到环境干扰的影响。文章提出了一种基于节点隶属度模糊化定位算法,能对节点测距信息模糊化处理以减少环境干扰和信号波动带来的定位偏差,具有较高的定位精度和稳定性。下一步工作将引入粒子群优化原理,结合模糊算法定位三维空间节点位置。
[1]鲍 微,徐 云,黄刘生,等. 无线传感器网络中的速度自适应追踪算法[J]. 计算机工程, 2010(2):81-85.
[2]石为人,熊志广,许 磊. 一种用于室内人员定位的RSSI定位算法[J]. 计算机工程与应用, 2010(17):124-128.
[3]金卫民,神显豪. 基于RSSI的室外无线传感网络自定位算法[J]. 计算机工程,2008(13):139-151.
[4]Li D,Kerry D Wong,Yu Hen Hu. Detection classification, and tracking of targets[J].IEEE Signal Processing Magazine, 2002(8):348-358.
[5]Gustafsson F.Mobile positioning using wireless networks[J]. IEEE Signal Processing Magazine.2005,22(4): 41-53.
[6]Karpinski M. Sensor networks for smart roads[A]. IEEE International Workshop on Sensor Networks and Systems for evasive Computing[C].2006:158-167.
[7]Denis B.Joint distributed synchronization and positioning in UWB Ad hoc networks using TOA[J]. IEEE Trans on Microwave Theory and Techniques.2006,154(4): 1896-1911.
Research of Fuzzy Localization in Wireless Sensor Networks
Li Feng
(Guangdong Communication Polytechnic, Guangzhou 510650, China)
RSSI algorithm localization accuracy is very high in theory, but it is vulnerable to environmental interference and signal fluctuations, and if pursued all the details will greatly increase the complexity of the algorithm. This paper put forward a fuzzy localization algorithm against the weak points of RSSI algorithm in Wireless Sensor Networks,and applied to the RSSI location model. The new algorithm uses ridge-shaped distribution to fuzzification original RSSI signal. Then feedback and refine results according to the degree of approximation. The bigger value of fuzzy coefficient, the stronger anti disturbance ability, but the nodes have more or more similar lattice close degree, can not reflect the true state of the node, so the coefficient m should be based on attenuation index and environmental interference. Finally, simulation experiment shows that, the new algorithm can reduce the impact of environmental interference and signal fluctuations compared with RSSI and DV-Hop algorithm, which has high localization accuracy and stability.
wireless sensor networks; membership degree; fuzzy algorithm; RSSI
2015-09-08;
2015-10-20。
广东省高等学校教学质量与教学改革工程(粤教高函[2013]13号);广东省高等职业教育教学改革项目(粤教高函[2014]205号);全国交通运输职业教育科研项目(2015B21)。
李 锋(1981-),男,硕士研究生,讲师,主要从事计算机系统结构和网络安全方向的研究。
1671-4598(2016)03-0186-04
10.16526/j.cnki.11-4762/tp.2016.03.050
TP393
A

