CIKS-128分组算法的相关密钥-差分攻击

郭建胜，崔竞一，罗 伟，刘翼鹏

(1.解放军信息工程大学，河南郑州 450004；2.信息保障技术重点实验室，北京 100000；3.78179部队，四川成都 611843)



CIKS-128分组算法的相关密钥-差分攻击

郭建胜1,2，崔竞一1，罗 伟3，刘翼鹏1

(1.解放军信息工程大学，河南郑州 450004；2.信息保障技术重点实验室，北京 100000；3.78179部队，四川成都 611843)

分析研究了CIKS-128分组密码算法在相关密钥-差分攻击下的安全性.利用DDP结构和非线性函数的差分信息泄漏规律构造了一条高概率相关密钥-差分特征，并给出攻击算法，恢复出了192bit密钥；在此基础上，对剩余64bit密钥进行穷举攻击，恢复出了算法的全部256bit密钥.攻击所需的计算复杂度为277次CIKS-128算法加密，数据复杂度为277个相关密钥-选择明文，存储复杂度为225.4字节存储空间.分析结果表明，CIKS-128算法在相关密钥-差分攻击条件下是不安全的.

分组密码；密码分析；CIKS-128分组算法；相关密钥-差分攻击

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.09.010

1 引言

随着物联网相关技术地快速发展，资源受限环境下的信息安全问题日益突出.这类硬件设备的计算、存储资源受限的环境下，常规的分组密码算法在资源占用率和实现效率上难以满足需求.DDP(Data-Dependent Permutations)[1,2]结构具有实现速率快、资源占用小、数据处理规模灵活等特点，被广泛应用于算法设计[3～5].基于DDP结构设计的密码算法具有高效低耗特点.然而，目前针对这类算法的安全性分析有待完善，严重制约了这类算法走向应用.

近年来，复合攻击方法的研究成为分组密码分析领域的研究热点，特别是相关密钥-差分类型的攻击方法的应用[6～10]极大推动了分组密码分析的发展.特别地，为减小计算-存储开销，基于DDP结构设计的分组密码算法通常选用简单的密钥生成算法，相关密钥类型的复合攻击成为分析这类算法的有力手段之一.2010年，Lee等人利用分割攻击的思想对DDP-64分组密码算法抵抗相关密钥-差分分析的能力进行了评估[11]；2012年，在WAINA会议上，Jinkeon Kang等人提出了针对MD-64算法的相关密钥-扩大飞来去器攻击[12]，为基于高次DDP结构的分组密码算法安全性分析提供了新的思路.

作为基于DDP结构的典型算法，CIKS-128算法[3]采用DDP结构提升了数据的处理效率，选用简单的密钥生成算法降低了实现功耗，设计者声称该算法能够抵抗所有已知攻击.针对CIKS-128算法，Youngdai Ko等人于2004年提出了相关密钥-差分攻击[13]，恢复出了47bit密钥信息；Lee等人于2011年构造了算法的一条高概率相关密钥-差分特征[14]，恢复出了63bit密钥信息，这是针对该算法最好的分析结果.

本文研究了CIKS-128算法的相关密钥-差分性质，利用DDP结构的差分信息泄漏规律构造了算法的高概率相关密钥-差分特征，并给出了相应攻击算法，恢复出了192bit密钥，并利用穷举攻击恢复出了算法剩余64bit密钥.攻击算法计算复杂度为277次CIKS-128算法加密，数据复杂度为277个选择明文，存储复杂度为225.4字节.

2 相关知识

2.1 符号约定

本文常用符号约定如下：

逐位模2加ei角标位置取值为1,其它位置为0的二元序列,ei1,i2,ei1,i2,i3依此类推P(C)明文(密文)XL(XR)数据块X的左(右)半部分ΔX表示二元序列X的两组取值逐位模2加X·Y表示二元序列X,Y逐位相乘xiX的第i比特X>>>n表示二元序列X循环右移nbitei→ej输入差分为ei,输出差分为ej的差分对pi,qi概率Pn/m输入输出为nbit,控制信息为mbit的DDP结构(变换)

2.2 CIKS-128分组密码算法

CIKS-128算法分组长度为128bit，密钥长度为256bit，迭代圈数为12轮，算法整体结构和圈函数结构如图1所示.

如图1所示，CIKS-128算法采用类Feistel结构，圈函数对右半部分处理后作为下一轮左半部分输入，左半部分直接输出作为下一轮右半部分输入，最后一轮圈函数变换后不进行左右数据块互换.特别地，圈函数左半部分数据和圈子密钥共同作为右半部分DDP结构的控制信息.

V=(V1,V2,V3,V4,V5,V6)=π(L,L′,L″)其中(L′,L″)∈{(L⨁A(1),L⨁A(4)),(L⨁A(3),L⨁A(2))}，L,A(i)∈{1,0}64,i=1,2,3,4.Vi取值如下：

线性变换∏由四个长度为16bit的轮换的乘积构成，可描述为

(1,50,9,42,17,34,25,26,33,18,41,10,49,2,57,58);

(3,64,43,24,19,48,59,8,35,32,11,56,51,16,27,40);(4,7,28,47,52,23,12,63,36,39,60,15,20,55,44,31);(5,14,13,6,21,62,29,54,37,46,45,38,53,30,61,22).

移位变换I输入输出均为64bit，若其输入为X=(X1,X2,…,X8)，则输出为

其中Xi∈{0,1}8.

非线性函数G定义为

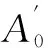
P64/192变换输入输出均为64bit，控制信息为192bit，图2给出了P64/192的结构图.P64/192由6层基本P2/1构成，每层包含32个并置的P2/1，层与层之间通过线性变换连接，其中基本单元P2/1定义为

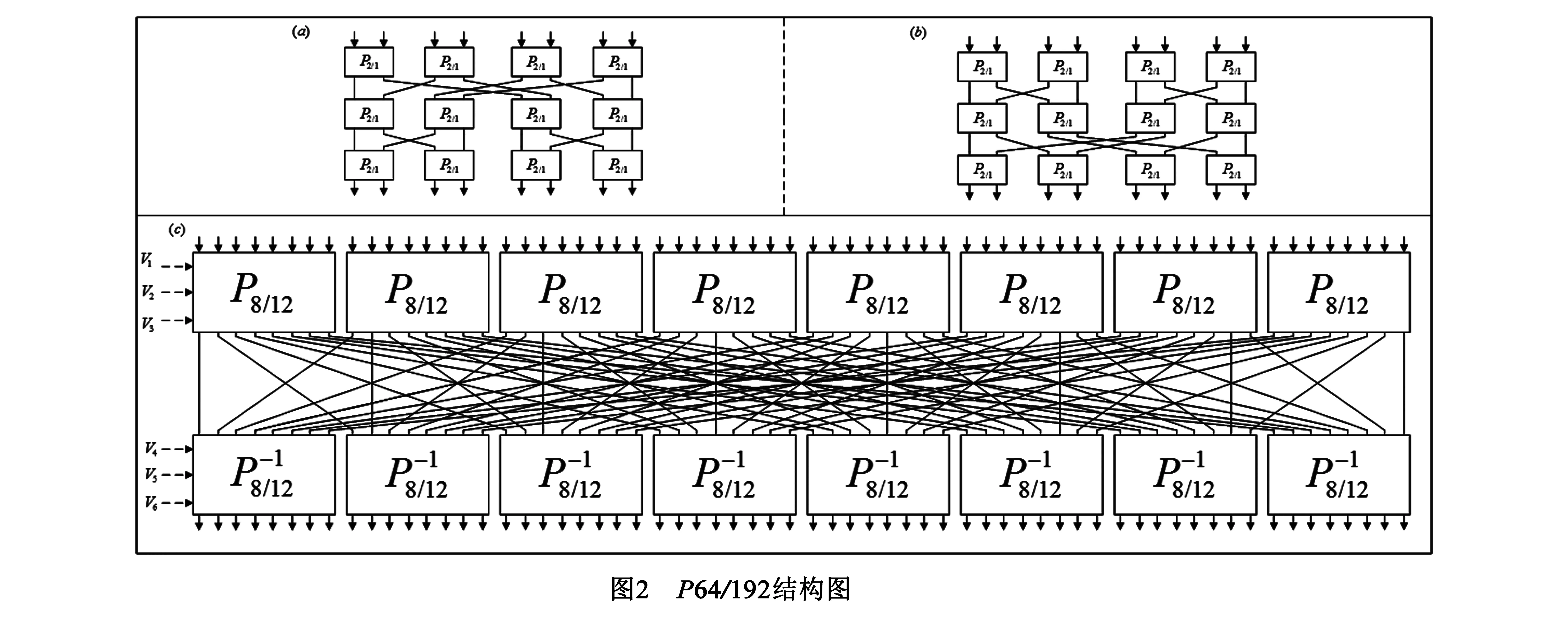
表1 CIKS-128算法圈子密钥

关于CIKS-128算法详细信息参见文献[3].

3 相关密钥-差分特性分析

定义1 重量表示二元序列中1的个数.

3.1 轮函数差分特性分析

下面分析第12轮输入差分ΔX12=(ej,0),密钥差分ΔQ12=(0,0,e64,e64)时，各变换环节的差分转移规律.

定义2 若DDP结构的控制信息差分重量为0时，输入输出重量相等，则称该DDP结构具有差分重量平衡性.

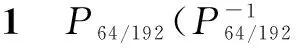
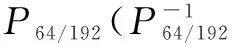
性质2 ΔX11=(0,0),ΔQ11=(e64,e64,0,0)时，ΔX12=(ej,0)的概率为2-9.

性质3 ΔX12=(ej,0)(j≠64),ΔQ12=(0,0,e64,e64)时，P64/192输出差分为0的概率为p1=2-4.

证明 由P2/1的定义，控制比特差分重量为1时，其输出差分为0的概率为2-1.由π的定义可知，圈函数左半部分输入差分重量为1时，P64/192的控制信息V的差分重量为3(不考虑密钥差分).由于j≠64，结合密钥差分(ΔA(1),ΔA(4))=(0,e64)后，控制信息V的差分重量为4.因此，P64/192输出差分为0的概率为p1=2-4.证毕.

性质4 ΔX12=(ej,0)(1≤j≤58),ΔQ12=(0,0,e64,e64)时，G1输出差分为ej的概率为p2=2-6.

证明 ΔX12=(ej,0),(ΔA′,ΔA″)=(0,0)时，G1输入差分为ej，其输出差分ΔW1满足：

由上式可知，ΔW1(i)=1的概率为0.5(i=j+1,j+2,j+3,j+4,j+5,j+6)，从而G1输出差分ΔW1=ej的概率为p2=2-6.证毕.

性质5 ΔX12=(ej,0)(1≤∏(j)≤58),ΔQ12=(0,0,e64,e64)时，G2输出差分为e∏(j)的概率为p3=2-7.

证明 根据定义，密钥差分(ΔA′,ΔA″)=(e64,e64)引起的输出差分满足ΔW1(64)=1⨁l63.又根据性质4的分析过程，1≤∏(j)≤58时，数据差分与密钥差分引起的输出差分非0比特位不重合，因此密钥差分对G2输出差分无影响的概率为2-1.根据性质4，ΔX12=(ej,0)(1≤∏(j)≤58)使得G2输出差分为e∏(j)的概率为2-6.因此，G2输出差分为e∏(j)的概率为p3=2-1×2-6=2-7.证毕.

证明 由性质3，4，5即得.证毕.

3.2 相关密钥差分特征

由∏变换的定义，“1≤j,∏(j)≤58”等价于“1≤j≤58且j≠3,12,21,30,39,48”.结合定理1和文献[14]给出的相关密钥-差分特征，表2给出了CIKS-128算法的相关密钥-差分特征，其中1≤j≤58且j≠3,12,21,30,39,48.

如表2所示，本文构造的相关密钥-差分特征概率为

(2-3)10×2-9×2-31.98≈2-71

3.3P64/192-1差分特性分析

记vi表示第12轮192比特的控制信息V′的第i比特.

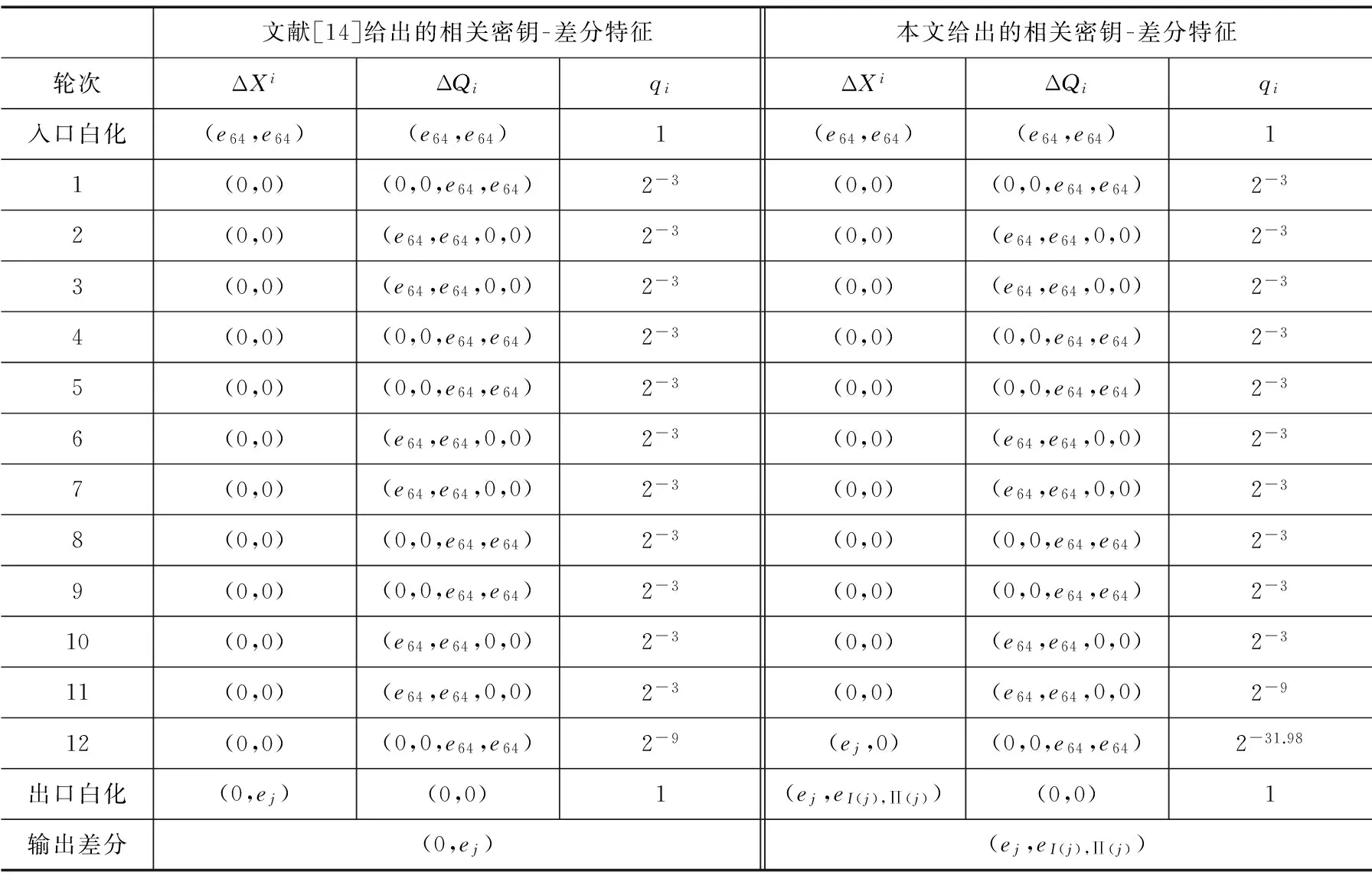
表2 相关密钥-差分特征

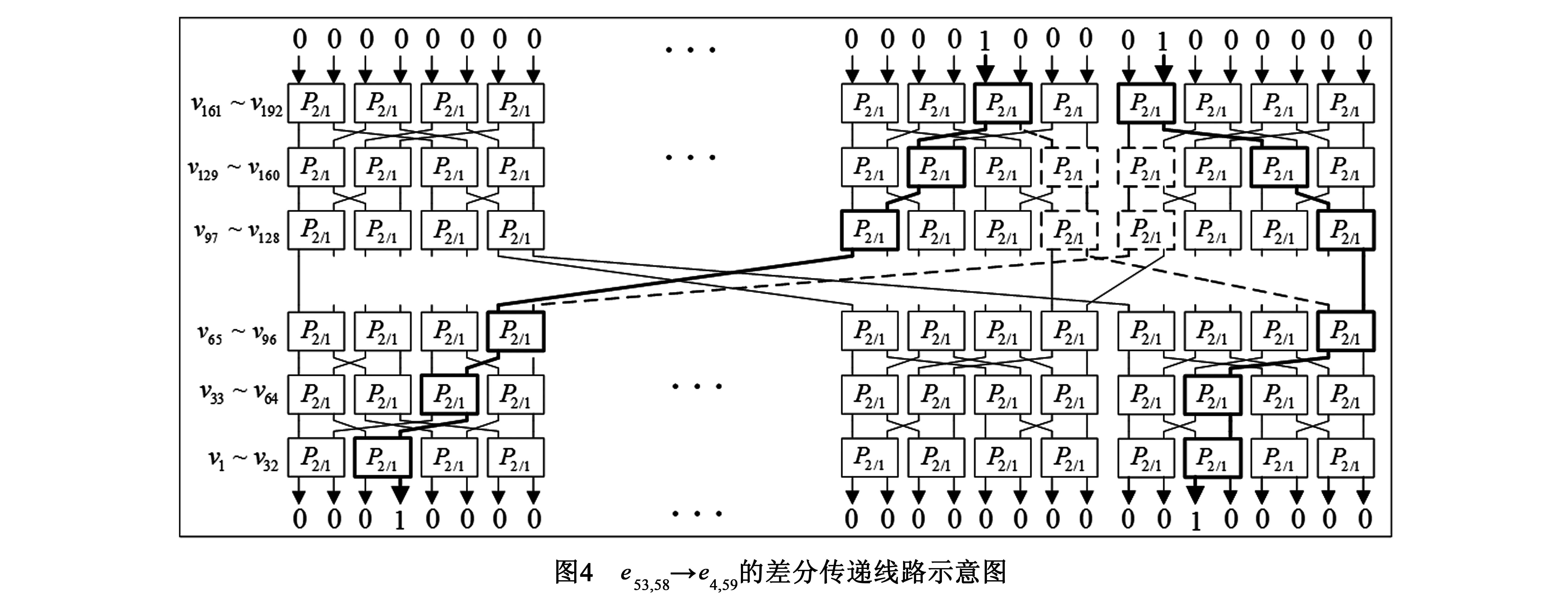
重量为2的差分对eI(j),∏(j)→es,t存在2类差分传递线路，每类包括两条重量为1的差分传递线路.例如j=57时，I(j)=53,∏(j)=58，e53,58→e4,59的两条差分传递线路由图4给出：第Ⅰ类差分传递线路中，e53传递到e4，e58传递到e59(如图4实线所示)；第Ⅱ类差分传递线路中，输入差分e53传递到e59，e58传递到e4(如图4虚线所示).e53,58→e4,59的差分传递线路由表3给出.

表3 e53,58→e4,59的两类差分传递线路

4 相关密钥-差分攻击算法

下面利用本文构造的相关密钥-差分特征，给出CIKS-128算法的相关密钥-差分攻击算法.

算法1 相关密钥-差分攻击算法对j=2,10,16,18,20,23,26,27,28,31,33,34,41,44,49,51,55,56,57执行以下步骤:Step1 选择n个满足差分X⊕X*=(e64,e64)的明文对(X,X*).Step2 利用密钥K,K*分别加密明文X,X*,得到相应的密文Y,Y*,其中K⊕K*=(0,0,e64,e64);对固定的s,t执行Step3～Step4:Step3 抛弃不满足Y⊕Y*=(ej,es,t)(1≤j≤58,j≠3,12,21,30,39,48)的密文对,利用重量为2的差分对eI(j),∏(j)→es,t恢复出第12轮P-164/192两组12bit控制信息,建立密文、控制信息与密钥块O1,O2,O3的方程组,将得到两组12bit密钥信息kjs,t,kj's,t作为整体存入集合Kjs,t.Step4 对集合Kjs,t中的12bit密钥比特链kjs,t,kj's,t分别计数,将计数次数不小于5次的12bit密钥链分别作为正确密钥,存入Kjs,t*;Step5 取另一组s,t执行Step3～Step4;Step6 整理得到Kj=∪s,tKjs,t*

攻击算法的成功率和复杂度分析分别由定理2和定理3给出.

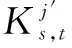
与此同时，错误密钥链的计数次数不小于5次的概率为

定理3n=276时，利用攻击算法能够恢复出CIKS-128算法的192比特密钥信息，计算复杂度为277次CIKS-128算法加密，数据复杂度为277个选择明文，存储复杂度为225.4字节.

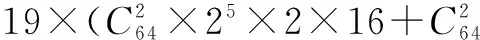
在利用攻击算法恢复出CIKS-128算法192比特密钥的基础上，对于剩余的64比特密钥信息进行穷举攻击，所需的计算复杂度为264次CIKS-128算法加密.由于264+277≈277，利用277次CIKS-128算法加密，277个相关密钥-选择明文以及225.4字节存储空间，即可恢复出CIKS-128算法全部256比特密钥.

5 结束语

基于DDP结构类的分组密码算法主要面向对密码算法的加解密速率和资源占用要求较高的硬件环境，因此算法大多选用简单的密钥生成算法，节省了密钥计算时间和存储空间.作为一种典型的基于DDP结构设计的分组密码算法，CIKS-128算法具有低能耗、高效率的特点.本文的分析结果表明，简单的密钥生成算法和DDP结构的差分重量平衡性，导致CIKS-128算法难以抵抗相关密钥-差分攻击.表4列出了部分典型分组密码算法在相关密钥-差分攻击条件下的最优攻击结果.

对比传统的差分攻击，相关密钥-差分攻击要求密钥生成算法具有较差的差分扩散特性.LBlock、AES-256的密钥生成算法差分扩散特性较好，相关密钥-差分攻击效果较差.作为基于DDP结构的典型分组密码算法，Cobra-H128、CIKS-128的密钥生成算法比较简单，密钥长度分别为128bit和256bit，与文献[17]相比，本文以相当的复杂度攻击得到了CIKS-128全部256密钥比特.针对CIKS-128算法，本文首次恢复出了算法的全部密钥比特，攻击结果明显优于Youngdai Ko和Lee给出的攻击结果.分析结果表明，利用DDP结构设计算法时，一应当充分考虑DDP结构的差分信息泄漏规律，在不影响效率的前提下，利用一些密码学指标较好的变换与DDP结构结合使用，提升圈函数密码学指标；二增强密钥生成算法的差分扩散性，降低各圈子密钥的相关性.

表4 部分算法在相关密钥-差分攻击下的攻击结果

[1]Moldovyan A A.Fast block ciphers based on controlled permutations[J].Computer Science Journal of Moldova,2000,8(3):270-283.

[2]Moldovyan A A,Moldovyan N A.A cipher based on data-dependent permutation[J].Journal of Cryptology,2002,15(1):61-72.

[3]Sklavos N,Moldovyan N A,Koufopavlou O.High speed networking security:design and implementation of two new DDP-based ciphers[J].Mobile Networks and Applications-MONET,2005,10(1-2):219-231.

[4]Minh N,Bac D,Duy H.New SDDO-based block cipher for wireless sensor network security[J].I.J.Computer Network and Network Security,2010,10(3):54-60.

[5]Bac Do Thi,Minh Nguyen Hieu,Duy Ho Ngoc.An effective and secure cipher based on SDDO[J].I.J.Computer Network and Information Security,2012,4(11)：1-10.

[6]Biryukov A,Nikolic I.Search for related-key differential characteristics in DES-Like ciphers[A].LNCS 6733:FSE 2011[C].Lyngby,Denmark:Springer,2011.18-34.

[7]Minier M,Naya-Plasencia M.A related key impossible differential attack against 22 rounds of the lightweight block cipher LBlock[J].Information Processing Letters,2012,112(16):624-629.

[8]詹英杰,关杰,丁林，等.对简化版LBLock 算法的相关密钥不可能差分攻击[J].电子与信息学报,2012,34(9):2161-2166.

Zhan Ying-jie,Guan Jie,Ding Lin,et al.Related-key impossible differential attack on reduced round LBlock[J].Journal of Electronics & Information Technology,2012,34(9):2161-2166.(in Chinese)

[9]Tomer Ashur,Orr Dunkelman.A practical related-key boomerang attack for the full MMB block cipher[A].LNCS 8257:Cryptology and Network Security 2013[C].Paraty,Brazil:Springer.2013.20-22.

[10]Marine Minier.On the security of piccolo lightweight block cipher against related-key impossible differentials[A].LNCS 8250:INDOCRYPR 2013[C].Mumbai,India:Springer,2013.308-318.

[11]Lee Changhoon,Lee Sangjin,Park Jong Hyuk,et al.Security analysis of pure DDP-based cipher proper for multimedia and ubiquitous device[J].Telecommunication System,2010,44(3-4):267-279.

[12]Kang Jinkeon,Jeong Kitae,Yeo Sang-Soo,et al.Related-key attack on the MD-64 block cipher suitable for pervasive computing environments[A].26th International Conference on Advanced Information Networking and Applications Workshops(WAINA 2012)[C].Fukuoka:IEEE,2012.726-731.

[13]Ko Youngdai,Lee Changhoon,Hong Seokhie,et al.Related-key attacks on DDP based ciphers:CIKS-128 and CIKS-128H[A].LNCS 3348:INDOCRYPT 2004[C].Chennai,India:Springer,2004.191-205.

[14]Lee Changhoon,Kim Jongsung,Sung Jaechul,et al.Cryptanalysis of CIKS-128 and CIKS-128H suitable for intelligent multimedia and ubiquitous computing systems[J].Computing and Informatics,2011,30(3):447-466.

[15]Shusheng Liu,Zheng Gong,Libian Wang.Improved related-key differential attacks on reduced-round LBlock[A].Information and Communications Security-14th International Conference(ICICS 2012)[C].Hong Kong,China:Springer,2012.58-69.

[16]Alex Biryukov,Dmitry Khovratovich,Ivica Nikoli′c.Distinguisher and related-key attack on the full AES-256[A].CRYPTO’09,Santa Barbara[C].CA,USA:Springer,2009.231-249.

[17]罗伟，郭建胜.Cobra-H64/128算法的相关密钥-差分攻击[J].电子学报，2013,41(8):1569-1573.

LUO Wei,GUO Jian-sheng.Related-key differetial attacks on cobra-H64/128[J].Acta Electronica Sinica,2013,41(8):1569-1573.(in Chinese)

郭建胜 男，1972年出生，河南沁阳人，博士，解放军信息工程大学教授、博士生导师，主要研究方向为密码学和信息安全.

E-mail:tsg-31@126.com

崔竞一(通讯作者) 男，1992出生，河南登封人，解放军信息工程大学硕士生，主要研究方向为密码分析.

E-mail:tsg-31@126.com

Related-Key Differential Attack on Block Cipher CIKS-128

GUO Jian-sheng1,2,CUI Jing-yi1,LUO Wei3,LIU Yi-peng1

(1.ThePLAInformationEngineeringUniversity,Zhengzhou,Henan450004,China;2.ScienceandTechnologyonInformationAssuranceLaboratory,Beijing100000,China;3.TheUnitof78179,Chengdu,Sichuan,611843,China)

The security of CIKS-128 block cipher under related-key differential attack was studied.A related-key differential of high probability was constructed with the differential information leakages in the structure of DDPs and nonlinear functions.By proposing a corresponding key recovery attack based on the related-key differential,the master key of 192 bits was recovered.The rest 64 bits of the master key could be obtained by exhaustive search.The computational complexity,the data complexity and the memory complexity are 277CIKS-128 block cipher encryptions,277chosen-plaintexts and 225.4bytes of storage resources,respectively.Analysis results show that CIKS-128 is unsafe under related-key differential attack.

block cipher;cryptanalysis;CIKS-128;related-key differential attack

2014-12-24；

2015-06-24；责任编辑：马兰英

博士后科学基金(No.2014M562582)

TN918.1

A

0372-2112 (2016)08-1837-08