环Z2m上一类常循环码的挠码及其应用

朱士信,孙中华,开晓山

(1.合肥工业大学数学学院,安徽合肥 230009;2.东南大学移动通信国家重点实验室,江苏南京 210096)



环Z2m上一类常循环码的挠码及其应用

朱士信1,2,孙中华1,开晓山1,2

(1.合肥工业大学数学学院,安徽合肥 230009;2.东南大学移动通信国家重点实验室,江苏南京 210096)

该文研究了环Z2m上任意长的(1+2λ)-常循环码的挠码及其应用.首先,给出环Z2m上(1+2λ)-常循环码的挠码.然后,利用挠码得到环Z2m上某些(1+2λ)-常循环码的齐次距离分布.同时,利用挠码证明了环Z2m上(2m-1-1)-常循环自对偶码都是类型I码,并利用这类码构造了极优的类型I码.

常循环码;挠码;自对偶码;距离分布

电子学报URL:http://www.ejournal.org.cn DOI:10.3969/j.issn.0372-2112.2016.08.008

1 引言

上世纪九十年代,Hammons等人在文献[1]中证明了一些高效的二元非线性码Kerdock码与Preparata码可以看作是Z4-线性码的二元像,从而使有限环上编码理论获得了突破进展.自此,许多学者对有限环上的纠错码进行了广泛而深入的研究.众所周知,码的距离是衡量码的纠错性能的一个重要参数.文献[2]完全计算了Z2a上长为2s的λ-常循环码的Hamming距离、齐次距离、Lee距离和欧几里得距离,其中λ为Ζ2a上形如(4k-1)的单位;文献[3]计算了GR(2a,m)上长为2s的负循环码的Hamming重量;文献[4]计算了F2+uF2上长为2e的循环码的各种距离分布.通常,确定有限环上线性码的各种距离是比较困难的.Norton与Sǎlǎgean在文献[5]中引入了有限链环上的线性码C的挠码概念,证明了C的Hamming距离等于它最高阶挠码的Hamming距离.后来,Doughert与Park[6]将挠码用于研究Zpm上循环码的结构;文献[7]利用挠码给出了环Fpm+uFpm+…+uk-1Fpm上任意长(1+u)-常循环码的齐次距离分布.由此可见,挠码在研究有限链环上线性码中起着重要作用.因此,确定有限链环上线性码的挠码是十分必要的.本文确立了整数剩余类环Z2m上任意长度的(1+2λ)-常循环码的挠码,然后将挠码应用于两方面:(1)研究了Z2m上(1+2λ)-常循环码的Hamming距离、齐次距离与欧几里得距离;(2)研究了Z2m上(2m-1-1)-常循环自对偶码,证明了这类常循环码是类型I码,并且利用这类码构造了极优类型I码.

2 预备知识

3 环Z2m上(1+2λ)-常循环码的挠码

为了计算Z2m上η-常循环码的挠码,其中η=1+2λ∈Z2m,λ是Z2m中的单位.首先给出几个重要的引理.记R=Z2m[x]/〈xN-η〉.

引理1 在R中,〈(xn-1)2s〉=〈2〉.

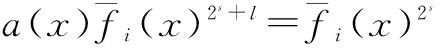
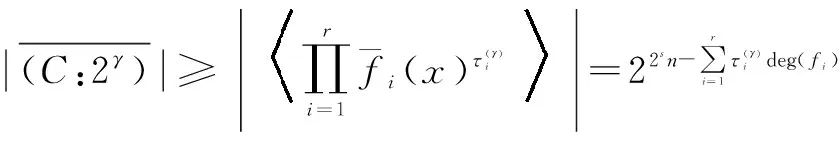
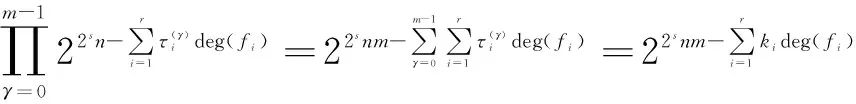
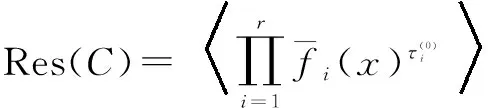
4 挠码的应用

4.1 环Z2m上(1+2λ)-常循环码的齐次距离

由于齐次距离在有限链环上有许多重要的应用,从而引起研究者们的关注.下面利用挠码确定某些Z2m上η-常循环码的确切的齐次距离,对一般Z2m上的η-常循环码,给出齐次距离的一个界.

定义1[2]环Z2m上的齐次重量定义为Z2m上的重量函数

(1)当γ0≤m-2时,2m-2dγ0≤dHom(C)≤2m-1dm-1.

(2)当γ0=m-1时,dHom(C)=2m-1dm-1.

(1)当0≤σ≤2s(m-2)时,dHom(C)=2m-2.

(2)当2s(m-2)+1≤σ≤2s(m-1)时,dHom(C)=2m-1.

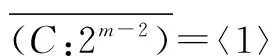
4.2 环Z2m上2m-1-1-常循环自对偶码

其中0≤si≤2sm.

定理4 环Z2m上长为N的ρ-常循环自对偶码都是类型I码.

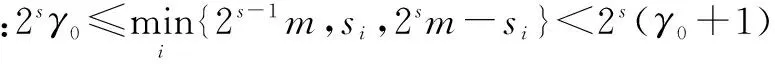
定理4指出环Z2m上的ρ-常循环自对偶码总是类型I码.文献[11]给出了Z2m上长为N的类型I码的欧几里得距离界:

若2⎣N/24」≤2m-3,则

(**)

当2⎣N/24」≤2m-3时,称Z2m上满足(**)界的类型I码为极优码.下面利用挠码构建Z2m上极优类型I码.

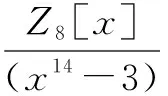
例3 在Z16[x]中,x7-1=f0(x)f1(x)f3(x),其中f0(x)=x-1,f1(x)=x3+6x2+5x-1,f3(x)=x3+11x2+10x-1.设C是Z16上长为14的7-常循环自对偶码,其生成多项式为g(x)=f0(x)4f1(x)5f3(x)3.在Z8[x]/(x14-7)中,g(x)=2x13+12x12+8x11+2x10+6x9+2x8+2x6+12x5+8x4+2x3+6x2+2x+4.

5 总结

本文给出了环Z2m上任意长的(1+2λ)-常循环码的挠码,利用挠码讨论了Z2m上(1+2λ)-常循环码的齐次距离分布,并证明了(2m-1-1)-常循环自对偶码为类型I码.最后,利用常循自对偶码,构造了Z8与Z16上极优的类型I码.一个值得考虑的问题是利用挠码研究Z2m上任意长度的循环码.

[1]A R Hammons,P V Kumar,A R Calderbank,N JA Sloane,P Solé.The Z4-linearity of Kerdock,Preparata,Goethals,and related codes[J].IEEE Transactions on Information Theory,1994,40(2):301-319.

[2]H Q Dinh.Complete distances of all negacyclic codes of length 2soverz2a[J].IEEE Transactions on Information Theory,2007,53(1):147-161.

[3]S Zhu,X Kai.The hamming distances of negacyclic codes of length 2sover GR(2a,m) [J].Journal of Systems Science and Complexity,2008,21(1):60-66.

[4]施敏加,杨善林,朱士信.环F2+uF2上长为2e的循环码的距离[J].电子学报,2011,39(1):29-34.

Shi Min-jia,Yang Shan-lin,Zhu Shi-xin.On minimum distance of cyclic codes of length 2eoverF2+uF2[J].Acta Electronica Sinica,2011,39(1):29-34.(in Chinese)

[5]G H Norton,A Salagean.On the hamming distance of linear and cyclic codes over a finite chain ring[J].IEEE Transactions on Information Theory,2000,46(3):1060-1067.

[6]S T Dougherty,Y H Park.On modular cyclic codes[J].Finite Fields and Their Application,2007,13(1):31-57.

[7]朱士信,黄素娟.环Fpm+uFpm+…+uk-1Fpm上(1+u)-常循环码的齐次距离分布[J].电子与信息学报,2013,35(11):2580-2583.

Zhu Shi-xin,Huang Su-juan.The distribution of homogeneous distance of(1+u)-constacyc-lic codes overFpm+uFpm+…+uk-1Fpm[J].Journal of Electronics and Information Technology,2013,35(11):2580-2583.(in Chinese)

[8]X Kai,S Zhu,Y Tang.Some constacyclic self-dual codes over the integers modulo 2m[J].Finite Fields and Their Applications,2012,18(2):258-270.

[9]S Zhu,X Kai.A class of constacyclic codes overzpm[J].Finite Fields and Their Applications,2010,16(4):243-254.

[10]S T Dougherty,T A Gulliver,M Harada.TypeⅡself-dual codes over finite rings and even unimodular lattices[J].Journal of Algebraic Combinatorics,1997,9(3):233-250.

[11]E Bannai,S T Dougherty,M Harada,M Oura.TypeⅡcodes,even unimodular lattices,and invariant rings[J].IEEE Transactions on Information Theory,1999,45(4):1194-1205.

朱士信 男,1962年生,教授,博士生导师,获国家级教学名师、国家“万人计划”教学名师荣誉称号.主要从事编码理论、序列密码与信息安全研究.

E-mail:zhushixin@hfut.edu.cn

孙中华(通信作者) 男,1989 年生,硕士研究生,研究方向为代数编码.

E-mail:sunzhonghuas@163.com

Torsion Codes of a Class of Constacyclic Codes over Z2mand Their Applications

ZHU Shi-xin1,2,SUN Zhong-hua1,KAI Xiao-shan1,2

(1.SchoolofMathematics,HefeiUniversityofTechnology,Hefei,Anhui230009,China;2.NationalMobileCommunicationsResearchLaboratory,SoutheastUniversity,Nanjing,Jiangsu210096,China)

The torsion codes and their applications of (1+2λ)-constacyclic codes over the ringZ2mof arbitrary lengths are studied.The torsion codes of (1+2λ)-constacyclic codes overZ2mare given firstly.Then by using the torsion codes,the homogeneous distance of some (1+2λ)-constacyclic codes is obtained and it is proved that all (2m-1-1)-constacyclic self-dual codes overZ2mare Type I.Some extreme Type I codes are constructed from such constacyclic codes.

constacyclic codes;torsion codes;self-dual codes;distance distribution

2015-01-08;

2015-09-07；责任编辑：蓝红杰

国家自然科学基金(No.61370089);安徽省自然科学基金(No.1508085SQA198，No.1508085MA13，No.1408085QF116);2014年安徽省高校优秀青年支持计划；东南大学移动通信国家重点实验室开放研究基金(No.2014D04)

TN911.22

A

0372-2112 (2016)08-1826-05