改进Hopkinson拉杆加载CT试样断裂数值模拟
邹广平,沈昕慧,吴立夫,唱忠良,杨丽红
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
改进Hopkinson拉杆加载CT试样断裂数值模拟
邹广平,沈昕慧,吴立夫,唱忠良,杨丽红
(哈尔滨工程大学 航天与建筑工程学院,哈尔滨 150001)
为研究紧凑拉伸(CT)试样的动态断裂性能,将分离式Hopkinson拉杆进行了改进,在入射杆与透射杆的加载端设计了一种夹持装置,实现了CT试样的动态断裂测试.采用ANSYS/LS-DYNA数值分析程序,对拉伸应力波加载下,基于改进后Hopkinson拉杆系统的CT试样动态断裂测试过程进行了数值模拟研究,得出CT试样的动态断裂响应,计算了表征其动态断裂韧性的相关参量.结果表明,试样中应力分布由非对称状态经约80 μs达到对称分布状态,此后试样应力分布云图对称,两端加载点载荷相等,试样达到应力平衡状态,满足了Hopkinson杆断裂韧性测试要求,并讨论了夹头截面突变与销钉直径对应力波传播和试样应力平衡的影响,为后续Hopkinson拉杆装置继续改进与CT试样动态断裂测试提供了依据.
冲击拉伸;动态断裂;Hopkinson拉杆;紧凑拉伸(CT)试样;数值模拟
动态断裂力学[1]在研究断裂问题时充分考虑了惯性效应,但与静态断裂问题相比,动态断裂问题不论是在数学上还是物理上都具有相当大的难度.因而,目前对于一般的动态断裂问题还没有形成可靠的理论.基于SHB(分离式Hopkinson杆)试验装置,学者试图在一维试验原理的基础上,更深入地了解材料的断裂行为.特别是在紧凑拉伸试样研究方面,比较具有代表性的研究有:Klepaczko[2]依照准静态的紧凑拉伸实验, 设计了一种被称为WLCT的楔形试件,使用Hopkinson压杆装置对其进行了断裂试验.考虑到楔形试件只是一种改进型的紧凑拉伸试样,故该研究不是严格的紧凑拉伸试样动态断裂研究;Corran等[3]使用了一种更合理的试样,在文献[2]方法的基础上,利用Hopkinson压杆装置完成了CT试件动态加载试验,并且首次讨论了与之相关的CT试件在动载荷下的平衡和摩擦问题;Bassim等[4]使用改进的分离式Hopkinson压杆对紧凑拉伸试样进行了应力波加载,确定了在准静态、慢速和动态加载下由J积分表示的断裂韧性的变化;Beguelin等[5]利用试验机在紧凑拉伸试样上施加不同的加载速率,通过比较由高速摄像机记录的光弹性实验结果与有限元分析结果,得到了试样动态效应与加载速率以及加载装置接触刚度之间的关系;邹广平等[6-7]基于改进的Hopkinson压杆装置,利用转换夹具的方法对CT试样进行了断裂韧性测试,同时用一种简单的弹簧质量模型来代表紧凑拉伸试样,将试样的动态应力强度因子表示为近似表达式,结合动态应力强度因子历史K(t)和电阻应变片测得的起裂时刻,获得了表征材料动态断裂韧性参量.Richard等[8]改进了CT试样,设计出紧凑拉伸剪切(CTS)试样进行了复合型裂纹断裂实验研究.
本文采用Hopkinson拉杆原理,设计了一种可以与入射杆和透射杆相连的夹持装置,通过有限元分析软件ANSYS/LS-DYNA对该加载方式的紧凑拉伸试样断裂实验进行数值仿真.通过数值模拟结果,得到夹持装置对试样响应的影响,验证了试样的应力平衡状态,并计算了表征其动态断裂韧性的相关参量.
1 数值模拟过程和结果
为了得到平面应变条件下材料的断裂韧性结果,试验中往往需要用到厚度较大的试样,但是受限于Hopkinson杆杆径尺寸,采用Hopkinson杆加载装置进行厚度较大的试样加载较为困难.针对这种情况,设计一种夹具,使得试样通过夹具与Hopkinson杆加载装置相连,从而极大地拓展了Hopkinson杆加载装置的应用范围.例如邹广平等[7]使用了一种杠杆形夹具,完成了基于SHPB的转换冲击拉伸,另外利用有限元方法分析了SHTB实验装置直接拉伸紧凑拉伸试样的动态断裂韧性测试[9];XU等[10]使用一种圆柱形夹头,通过Hopkinson拉杆装置完成了哑铃型试样的Ⅰ型和Ⅱ型动态断裂韧性的研究等.ULE等[11-12]采用带有周边切口的短金属圆柱试件,进行了平面应变型弹塑性静、动态断裂韧度试验研究;韩小平[13]等利用Hopkinson杆加载装置,对带有单边切口的纤维增强复合材料板试件进行动态断裂研究.本文采用了一种空心开槽圆柱夹头,其几何构型和尺寸如图1所示.夹头和试样利用销钉连接.入射杆和透射杆的长度为2 000 mm,直径均为16 mm.

图1 夹头的几何尺寸(单位:mm)
在夹头末端内壁和波导杆连接段分别攻螺纹,使得夹头和入射杆之间实现螺纹连接,然后使用销钉将试样与夹头开槽端连接.在透射杆上也使用相同的夹头,即实现了冲击拉伸过程中入射杆-夹具-试样-夹具-透射杆的连接.本文所采用的紧凑拉伸试样几何参数也是按照GB 4161—2007-T设计的,B=12 mm,W=32 mm,a/W=0.5.
1.1 有限元模型建立
前处理工作主要包括选取单元类型、指定材料模型、创建几何实体模型、进行网格划分、定义PART或组元、定义接触信息、添加边界条件、施加载荷等.
1.1.1 单元和材料模型的选用
本文采用8节点显式动力分析单元SOLID164.根据问题的需要,建模过程中采用了两种材料模型,分别为:1)各向同性弹性模型(isotropic).用于模拟入射杆、透射杆、夹头以及销钉的材料为高碳钢;2)双线性随动材料模型(BKIN).该材料模型是一种典型应变率无关的双线性随动硬化模型,用来模拟紧凑拉伸试样.建模时设定紧凑拉伸试样材料为率无关材料LY12cz铝合金.材料参数可以由准静态试验测得,其弹性模量为68.3 GPa,切线模量为88.1 MPa,失效应变为0.18.
1.1.2 创建几何模型
几何建模采用两种建模思路:入射和透射杆、夹头和销钉的几何构型相对简单,故选取自顶向下的建模方法;紧凑拉伸试样几何构型相对复杂,故选取自底向上的建模方法.模型如图2,3所示.

图2 入射杆-夹头的三维几何模型

图3 紧凑拉伸试样二维截面模型
Fig.3 Two-dimensional cross section model of the compact tension specimen
1.1.3 划分网格及接触设置
通过扫略、映射的方法,划分网格后的有限元模型如图4,5所示.

图4 入射杆-夹头的有限元模型
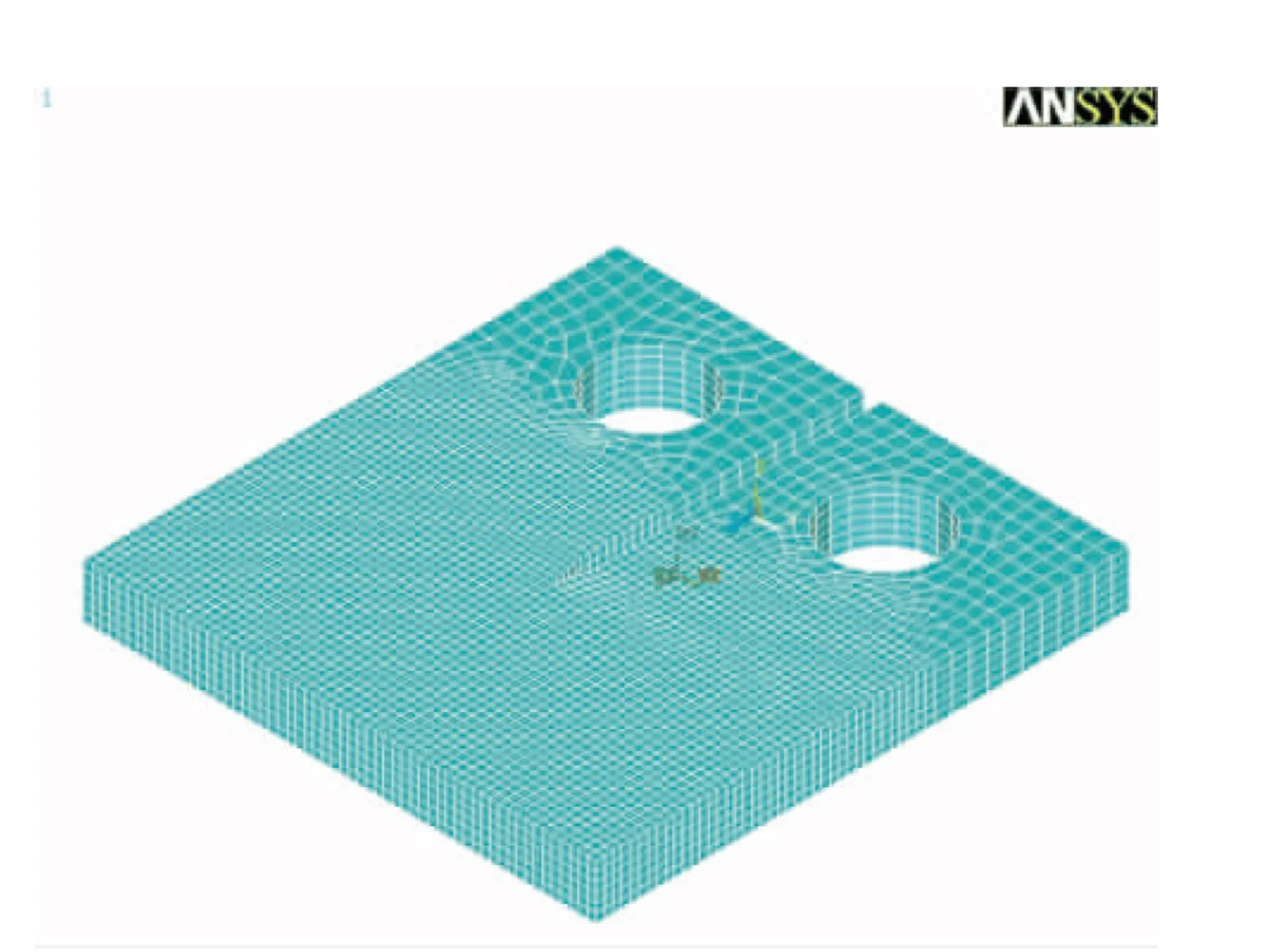
图5 紧凑拉伸试样的三维有限元模型图
Fig.5 3-D finite element model diagram of compact tension specimens
1.2 加载和求解
本文中加载曲线是由冲击拉伸试验测得波形数据(如图6所示)通过滤波光滑后得到入射波形曲线,如图7所示.
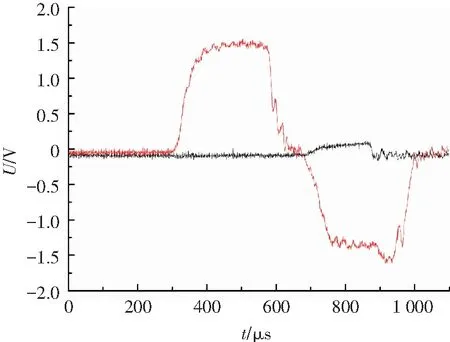
图6 试验测得的电信号
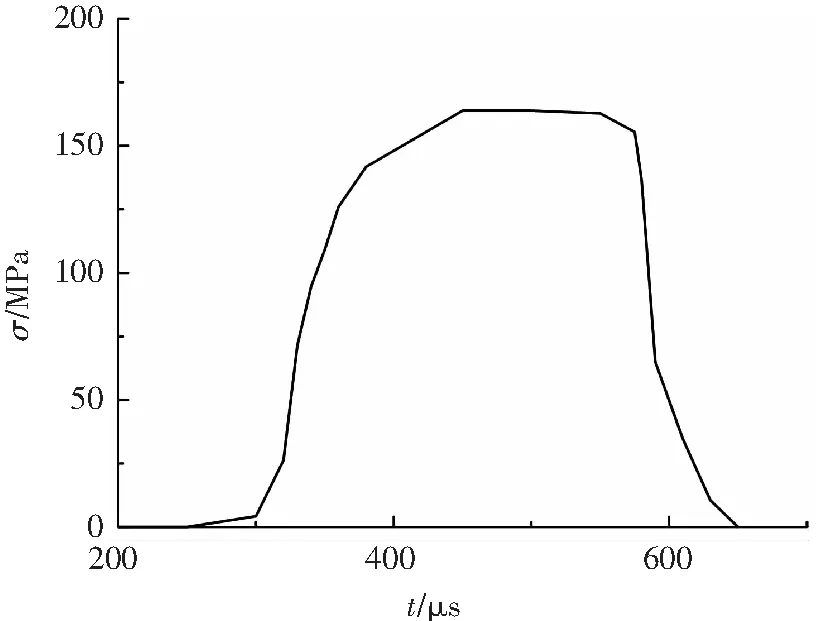
图7 入射波载荷曲线
2 数值模拟结果与分析
2.1 应力波的传播
选取试样厚度方向对称截面进行观察,可以看到应力波在试样中传播规律如图8所示,图8中为Von Mises stress(V-M)云图.

图8 应力波在CT试样中的传播
注:彩图见电子版(http://hit. alljournals.cn)(2016年第10期)
由图8可以看出,720.16 μs时应力波开始传入到试样中,开始时试样中的应力分布是非对称的,一段时间后逐渐达到对称分布状态,此时可认为试样已处于动应力平衡状态,试样达到应力平衡状态约经过80 μs,本文将从试样裂纹尖端处的应变和动态载荷两方面验证试样动应力平衡情况.
2.2 入射波、反射波和透射波的波形
查看入射杆和透射杆上单元的计算结果得到入射、反射和透射波形,如图9所示.图9中入射波和反射波是距入射杆端部1 000 mm处单元的计算结果;透射波是距透射杆端部1 000 mm处单元的计算结果.
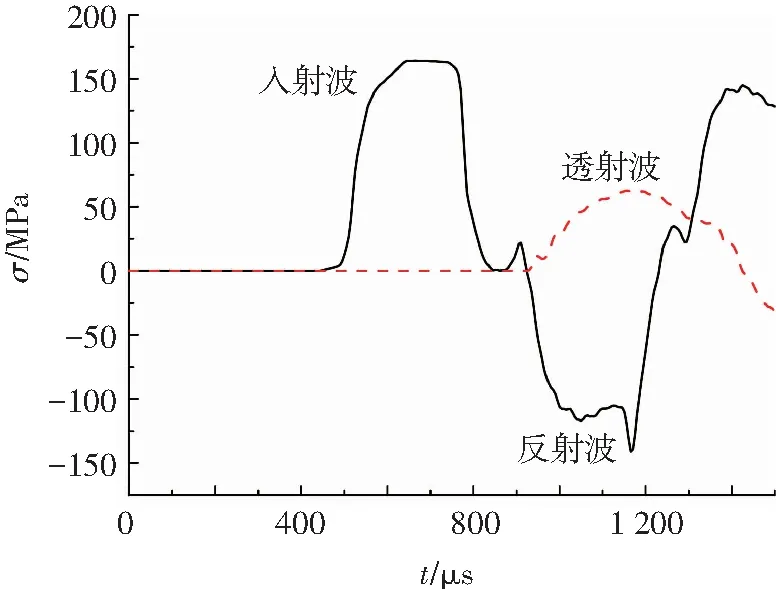
图9 入射波、反射波和透射波波形
Fig.9 Waveform of incident wave, reflected wave and transmission wave
由数值模拟可知:入射应力波脉冲的持续时间约为400 μs,但在应力波作用于试样上82.3 μs后,试样就达到了动态平衡,这时裂纹并未发生扩展.但是由反射波形可以看出:试样的反射波在900 μs和1 170 μs明显存在两个“尖点”.本文认为,这是因为夹头的使用对试验结果产生了影响.由夹头和Hopkinson杆连接方式不难看出,安装夹头后在波的传递路径上出现了截面突变,应力波从小截面传入到大截面中.为得到更严谨的结论,本文做了一个简单的类比仿真试验,试验模型如图10所示.夹头和试样均被简化为实心圆柱,且在圆柱形试样的另一端添加了无反射边界条件,仅对入射和反射波形加以研究,得到的入射和反射波形如图11所示.

图10 类比试验模型示意

图11 类比试验波形
类比试验波形中同样出现了两个“尖点”,且与大试样冲击拉伸试验波形中两个“尖点”出现的时间吻合,说明夹头产生的截面突变是产生上述现象的主要原因.
2.3 应力平衡分析
在Hopkinson杆加载的断裂试验中要得到可靠的断裂韧性,必须满足两个基本假设:1)一维应力波;2)试样在起裂之前处于应力平衡状态.本文通过对试样裂尖两端单元的应力分析(如图12所示)和试样与入射杆和透射杆接触两端的动载荷比较结果(如图13所示),研究在该实验装置下的应力平衡情况.
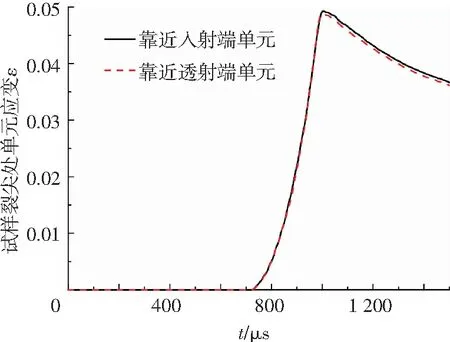
图12 试样裂尖单元的应变结果

图13 试样两端动载荷曲线
图12为试样裂尖单元的应变结果.从图12中可以看出:在725 μs时,试件开始受载;大约在810 μs时,裂尖单元应变值相等,达到了应力平衡.而CT试样的起裂时间在约1 000 μs,此时试样已经处于应力平衡状态,能够满足应力平衡假设.应力波传入试样到试样动应力平衡经历的时间约为85 μs.图13为试样两端动载荷曲线,其中P入射杆为入射杆加载点与试样之间的动载荷,P透射杆为试样与透射杆之间的动载荷.其计算公式为:P入射杆=EA(εI+εR),P透射杆=EAεT,E、A分别为Hopkinson杆的弹性模量和横截面积,εI、εR和εT分别为入射波、反射波和透射波应变,令试样开始受载时刻为0,从图13中可以得到与图14相似的结果,约82.3 μs,试样两端动载荷相等,试样处于动应力平衡状态.通过两种方法对应力平衡的验证,说明了该实验测试试样的动态断裂韧性方法的有效性,试样起裂发生在试样应力平衡之后,满足Hopkinson杆假设.
3 动态J积分的计算
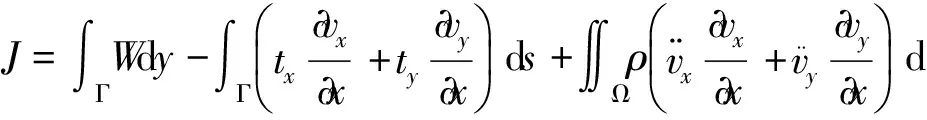
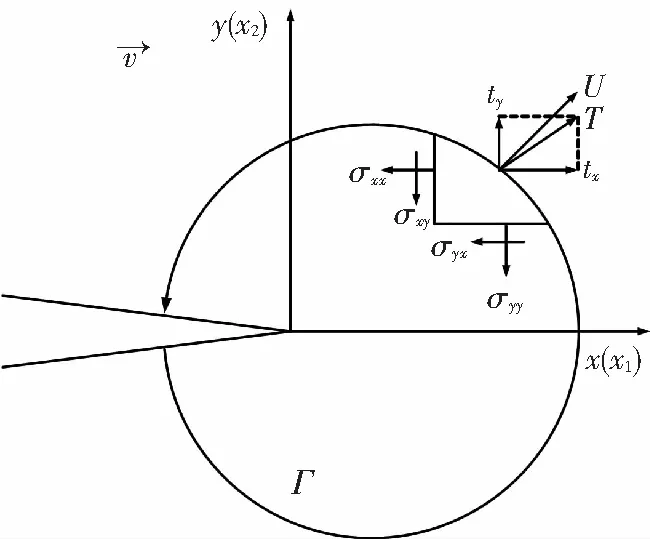
图14 J积分定义的区域
4 装夹条件的影响
本文在数值模拟时,尝试采用不同直径的销钉对夹头和试样进行连接.数值计算结果表明,对于相同的孔径(Ф8)而言,不同的装夹条件会产生不同的结果.当采用较大直径(Ф7.975)的销钉时,实验结果如上文所述,当其他条件均相同时,采用小直径(Ф7.400)销钉时得到的透射应力波曲线,如图15所示.
应力波曲线表明,当应力波传至试样时,试样上的平均应力迅速增加,但随后又出现了急剧的下降.这很可能是在加载的某一时刻,由于销钉的振动而发生了试样与销钉、夹具脱离的现象,在试验中这是不希望发生的.为消除这一现象,加大了销钉的直径,使各构件之间的配合更为紧密,即完成了上述所述试验.通过观察大直径销钉连接时的透射应力波曲线,发现脱离现象得到了较为显著的抑制.

图15 小直径销钉连接时的透射应力波曲线
此外,数值模拟表明销钉的直径对试样达到动态平衡所需时间也有影响,采用小直径销钉时试样上的应力波传播如图16所示,为VonMisesstress(V-M)云图.由图16可见,应力波在780μs时刻传入试样中,在试样上进行了多次反射,最终试样达到动态平衡历约100μs,长于大直径销钉时的情形.
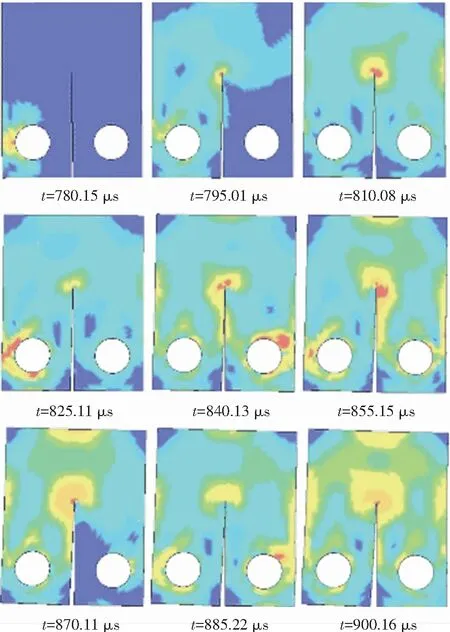
图16 采用小直径销钉时试样上的应力波传播
Fig.16Propagationofstresswaveusingsmalldiameterpinconnection
注:彩图见电子版(http://hit. alljournals.cn)(2016年第10期)
5 结 论
1)试样中应力分布云图在其开裂前可以达到对称分布状态,通过试样裂尖单元应变分析与杆系加载点载荷分析表明,采用改进后Hopkinson杆进行CT试样断裂测试,满足试样两端动应力平衡条件,满足动态断裂测试要求.
2)夹头截面突变对应力波传播有一定影响,但通过CT试样动态J积分计算,表明其并不影响断裂测试结果,也说明了改进方法的有效性.
3)销钉直径对试样达到动态平衡所需时间有影响,在试验测试中应予以关注.
[1] 范天佑.断裂动力学原理与应用[M].北京:北京理工大学出版社2006:3-4,10-14,17-18.
FAN Tianyou. The principles and applications of fracture kinetics[M].Beijing: Beijing Institute of Technology Press, 2006:3-4,10-14,17-18.
[2] KLEPACZKO J. Application of the split Hopkinson pressure bar to fracture dynamics[C]//Proceedings of the 2nd Conf. Mechanical Properties of Materials at High Rates ofStrain.Oxford, England: [s.n.], 1979: 201-214.
[3] CORRAN R S J,BENITTEZ F G,HARDING R, et al. Towards the development of a dynamic fracture initiation test[M].Berlin: Springer Netherlands, 1984:443-454.DOI: 10.1007/978-94-009-6146-3_27.
[4] BASSIM M N, BAYOUMI M R, SHUM D. Study of the variation of fracture toughness with loading rate using compact tension specimens [J]. Engineering Fracture Mechanics, 1987, 26(4): 619-623. DOI: 10.1016/0013-7944(87)90103-2.
[5] BEGUELIN P H, FOND C, KAUSCH HH. The influence of inertial effects on the fracture of rapidly loaded compact tension specimens Part A: loading and fracture initiation[J]. International Journal of Fracture,1998,89(1):85-102. DOI: 10.1023/A:1007457914776.
[6] 邹广平. 金属材料动态断裂韧性的表征与测试[D]. 哈尔滨:哈尔滨工程大学,2005:7-12.
ZOU Guangping. The metallic materials characterization and testing about dynamic fracture toughness[D]. Harbin :Harbin Engineering University ,2005:7-12.
[7] 邹广平, 唱忠良, 曲嘉, 等. 平面应变下紧凑拉伸试样的动态断裂韧性研究[J]. 实验力学, 2011, 26(3): 240-246.
ZOU Guangping, CHANG Zhongliang, QU Jia, et al. Experimental study of dynamic fracture toughness of specimen subjected to compact tension under plane strain[J]. Journal of Experimental Mechanics, 2011, 26(3): 240-246.
[8] RICHARD H A, SCHRAMM B, SCHIRMEISEN N H. Cracks on mixed mode loading-theories, experiments, simulations[J]. International Journal of Fatigue, 2014, 62: 93-103. DOI: 10.1016/j.ijfatigue.2013.06.019.
[9] 邹广平,沈昕慧,赵伟玲,等.SHTB加载紧凑拉伸试样断裂韧性测试仿真[J].哈尔滨工程大学学报,2015,36(7):917-921.DOI: 10.3969/j.issn.1006-7043.201404076.
ZOU Guangping, SHEN Xinhui, ZHAO Weiling, et al. Numerical simulation of dynamic fracture toughness tests on the compact tension specimen loaded by SHTB[J].Journal of Harbin Engineering University, 2015,36(7):917-921.DOI: 10.3969/j.issn.1006-7043.201404076.
[10]XU Zejian, LI Yulong. A novel method in determination of dynamic fracture toughness under mixed mode I/II impact loading [J]. International Journal of Solids and Structures, 2012, 49(2): 366-376. DOI: 10.1016/j.ijsolstr.2011.10.011.
[12]宫能平,夏源明. 周边切口短圆柱试件的杆杆型冲击拉伸试验系统的弹塑性有限元分析[J].固体力学学报, 2002,23(2):223-231.DOI:10.3969/j.issn.0254-7805.2002.02.016.
GONG Nengping,XIA Yuanming. Elastic-plastic fem analysis for the bar-bar tensile impact apparatus with a circumferentially notched short metal bar[J]. Acta Mechanica Solida Sinica, 2002,23(2):223-231. DOI:10.3969/j.issn.0254-7805.2002.02.016.
[13]韩小平,曹效昂,朱西平.冲击载荷下CFRP及GFRP层板断裂韧性的研究[J]. 复合材料学报,2007,24(2):137-142.DOI:10.3321/j.issn.1000-3851.2007.02.024.
HAN Xiaoping,CAO Xiaoang,ZHU Xiping. Fracture toughness research of CFRP and GFRP laminates under impact load[J]. Acta Materiae Compositae Sinica, 2007,24 (2)137-142.DOI:10.3321/j.issn.1000-3851.2007.02.024.
[14]KISHIMOTO K, AOKI S, SAKATA M. Dynamic stress intensity factors using J-integral and finite element method[J]. Engineering Fracture Mechanics, 1980, 13(2): 387-394. DOI: 10.1016/0013-7944(80)90067-3.
[15]XIA Yuanming, RAO Shiguo, YANG Baochang. A novel method for measuring plane stress dynamic fracture toughness[J].Engineering Fracture Mechanics,1994,48(1):17-24.DOI:10.1016/0013-7944(94)90139-2.
(编辑 张 红)
Fracture numerical simulation of CT specimen loaded by improved Hopkinson tensile bar
ZOU Guangping, SHEN Xinhui, WU Lifu, CHANG Zhongliang,YANG Lihong
(College of Aerospace and Civil Engineering,Harbin Engineering University,Harbin 150001,China)
To study the dynamic fracture performance about the compact tension(CT)specimen, the split Hopkinson bar was improved, and a kind of clamping device between the loading point of incident bar and transmission bar was designed to study the dynamic fracture test on the CT specimen. In terms of tensile stress wave propagation, the finite element method based on ANSYS/LS-DYNA had been adopted to realize the dynamic fracture response and calculate the relative parameters about the dynamic fracture toughness. The result shows that, the stress distribution in the CT specimens from the asymmetric state to the symmetric distribution needs about 80 μs, and then stress distribution cloud in the specimen becomes symmetric and the stresses on two points become equal. Thus the CT specimens come to the balance state, meeting the dynamic fracture toughness test requirements. The effect of the chuck section and the pin diameter on the stress wave propagation and stress balance was studied, which will provide the basis for the further research on the Hopkinson tensile bar and the dynamic fracture test on the CT specimens.
impact tension; dynamic fracture; Hopkinson tensile bar; compact tension (CT) specimen; numerical simulation
10.11918/j.issn.0367-6234.2016.10.021
2015-03-16
国家自然科学基金(11372081)
邹广平(1963—),男,教授,博士生导师
唱忠良,lxsy@hrbeu.edu.cn
O347.3
A
0367-6234(2016)10-0142-06

