钢管混凝土结构的可靠性分析理论及研究进展

陈少杰 王宏伟

（广州大学 土木工程学院）

钢管混凝土结构的可靠性分析理论及研究进展

陈少杰 王宏伟

（广州大学 土木工程学院）

结构可靠度理论的发展为钢管混凝土结构的可靠性分析提供了常用的概率分布和计算方法。根据钢管混凝土结构的承载力计算公式和四种影响误差，可以计算出其可靠度，与可靠指标比较，判断结构是否可靠。钢管混凝土结构可靠性分析的研究现状表明：由于试验数据有限、计算方法复杂、承载力计算公式不统一等问题，钢管混凝土结构的可靠性分析需要进一步的发展。

钢管混凝土结构；可靠性分析；概率分布；目标可靠指标；模型误差

1 引言

钢管混凝土构件是指在钢管中浇灌混凝土，让钢管和混凝土共同作用的组合构件。钢管混凝土构件具承载力高；抗震、防火性能优越；截面尺寸小、自重轻等优点，在各种建筑结构中广泛应用。

1993年，钟善桐教授［1］提出了“钢管混凝土统一理论”，把钢管和内填混凝土视为一个整体来研究和分析其性能，使钢管混凝土结构的研究和应用迅速发展。2012年，卢德辉［2］对钢管混凝土轴压承载力计算公式进行了修正，修正后的公式可直接根据空心率进行实、空心钢管混凝土构件的轴压承载力计算，更加方便统一。2014年12月《钢管混凝土结构技术规范》（GB50396-2014）［3］开始实施，为钢管混凝土结构设计、构件制作以及工程施工提供了指导。

目前国际上关于建筑工程的结构设计，普遍采用以结构可靠度为基础的概率定值设计法［4］。而国内外关于钢管混凝土结构的可靠度并没有系统的研究。通过对钢管混凝土构件的可靠性分析，在结构设计时可以降低结构的失效概率，可以为钢管混凝土结构的设计和优化提供理论指导。

2 结构可靠度理论

1946年，美国的Freudenthal［5］开创了安全度的研究工作。1947年苏联尔然尼钦等学者提出了一次二阶矩的基本概念，并提出了计算结构失效概率的方法和计算可靠度指标的公式。美国混凝土学会（ACI）于1964年成立了“结构安全度委员会”，系统地研究结构安全度的问题，A.H-S.Ang［6］发展了对各种不同结构的不确定性做了分析，提出了广义可靠性的概念。1969年美国的Cornell［7］提出了用可靠度指标β作为度量结构安全度的标准，并建立了计算结构安全度的二阶矩模式。B. Ellingwood［8］在荷载方面，C.C.Tung［9］在桥梁动力分析的概率方面，T.V.Galambos［10］在钢结构方面，Jame T.P. Yao［11］和Davaid Blockley［12］在模糊数学的安全度应用方面做了相关的研究。1971年加拿大的Lind［13］提出分项系数的概念，以便与设计规范联系起来，使可靠性分析的理论和方法达到实用阶段。

我国从20世纪50年代开始，开展了极限状态设计法的研究。1983年，《建筑结构设计统一标准》（GBJ68-1984）［14］开始实施；1992年，中国建筑科学研究院编制《工程结构可靠度设计统一标准》（GB50153-1992）［15］；2001年，《建筑结构可靠度设计统一标准》（GB50068-2001）［16］实施，促进了建筑结构使用性能的改善和可靠度设计方法的发展。

3 结构可靠性分析方法

3.1 可靠性分析常用的概率分布

结构可靠性分析常用的概率分布有以下几种：①正态分布；②对数正态分布；③耿贝尔分布；④威布尔分布；⑤伽马分布。

钢管混凝土结构可靠度分析中，结构的材料强度、构件重量、几何尺寸常假定服从正态分布；结构的抗力常假定服从对数正态分布；结构的荷载效应常假定服从耿贝尔分布；威布尔分布常用于模拟钢管混凝土结构的疲劳寿命和损失破坏模型；伽马分布常用于模拟钢管混凝土结构强度随时间衰减变化的随机过程。

3.2 结构可靠度的计算方法

结构可靠度的计算方法有以下几种：①中心点法；②验算点法；③当量正态化法；④蒙特卡洛法。

对于非线性极限状态方程，中心点法和验算点法计算得到的结果是近似的。实际工程中大多变量都不是正态变量，变量分布形式的不同和变量的相关性，对结构可靠指标的影响较大。采用当量正态化法，可以将非正态分布的变量转换成等效正态分布，随后用验算点法计算结构的可靠指标。蒙特卡洛法本质上是一种数值模拟的过程，不考虑功能函数的复杂性，回避了结构可靠度分析中的数学困难。计算机的发展和计算技术的提高使蒙特卡洛法的应用范围越加广泛。

4 钢管混凝土结构的可靠度

4.1 钢管混凝土结构的可靠指标

《钢管混凝土结构技术规范》（GB50396-2014）［3］中对钢管混凝土结构的可靠指标并没有明确说明。根据《建筑结构可靠度设计统一标准》（GB50068-2001）［16］，对于安全等级为二级的建筑结构，实心钢管混凝土结构在轴向受压时，套箍系数对构件的破坏形式影响较大，当套箍系数θ≥0.6时，一般发生延性破坏，应取目标可靠指标β=3.2；当套箍系数θ＜0.6时，一般发生脆性破坏，应取目标可靠指标β=3.7.而空心钢管混凝土结构在轴向受压时，由于空心部分的存在，一般发生脆性破坏，应取目标可靠指标β=3.7。

4.2 影响钢管混凝土结构可靠度的误差

影响结构可靠度的误差有抗力误差和荷载误差。抗力误差包括：①计算模误差；②材料性能误差；③几何参数误差。

计算模型误差主要是指计算公式中所采用的基本假定或近似简化不完全符合实际、计算公式本身的不精确等引起的误差。材料性能误差主要是指材料质量因素以及制作工艺、加载方式、环境等因素引起的结构中材料性能的差异。几何参数误差主要是指由于制作、安装等原因，设计的构件和制作安装后的实际构件之间几何上的差异。

4.3 钢管混凝土结构的承载力计算公式

根据《钢管混凝土结构技术规范》（GB50396-2014）［3］，钢管混凝土短柱的轴心受压承载力应按以下公式计算：

Rc=（1.212+Bθ+Cθ2）fscAsc（式1）

文献［2］考虑了空心率及施工方法对空心钢管混凝土构件组合强度的影响，对套箍系数和混凝土抗压强度调整系数进行了修正。修正后的公式如下：

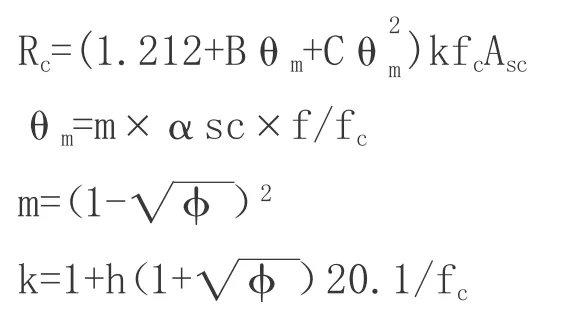
根据以上公式，考虑计算模型误差，把钢管混凝土的材料性能、几何参数代入公式中，结合结构的荷载效应建立极限状态方程，即可计算出钢管混凝土结构的可靠度。将可靠度与可靠指标进行对比，即可判断结构是否可靠。

5 钢管混凝土结构的可靠性研究现状

5.1 实心钢管混凝土结构的可靠性研究现状

2000年，陶忠［17］采用一次二阶矩法，对圆、方钢管混凝土轴压构件、纯弯构件和压弯构件的承载力公式进行了可靠性分析。结果表明：规程中钢管混凝土构件设计公式基本满足对塑性材料可靠指标的要求。

2003年，覃亚伟［18］利用神经网络优化Monte Carlo法计算了钢管混凝土柱的可靠度，为钢管混凝土结构的可靠度分析提供了一种新的计算方法。

2004年，肖国涛［19］采用Monte Carlo法，对圆钢管混凝土轴压短柱进行了可靠性分析，研究了不同材料强度、含钢率、荷载效应比对其可靠度的影响。

2005年，许成祥［20］采用Monte Carlo法，根据结构在小震作用下控制面失效的相关性和结构总体破坏指标的极限状态方程，分别进行了小震作用下和大震作用下钢管混凝土框架结构的可靠性分析。

2006年，余志武［21］采用一次二阶矩法，对圆钢管混凝土短柱在轴向压力作用下的可靠度进行了校准。结果表明：钢管混凝土构件的可靠指标随着混凝土强度等级的提高而提高，随着钢材强度、含钢率、套箍系数的提高而降低。

2006年，蔡小萍［22］利用Matlab的优化工具箱，将服从任意分布的随机变量转换为标准正态随机变量，对钢管混凝土轴压短柱进行了可靠性分析，计算的可靠指标与JC法计算结果一致。

2008年，李飞［23］采用Monte Carlo法和响应面法，对钢管混凝土结构进行了可靠度分析和优化设计。提出了结构分析—优化设计—结构分析的结构优化设计过程，在满足承载力要求的条件下，使材料的分布更加合理。

2009年，周圣斌［24］采用Monte Carlo法，对钢管混凝土柱的极限承载能力进行了可靠度分析，研究了材料性能、荷载组合、荷载效应比和含钢量对钢管混凝土柱可靠度的影响。

2010年，肖阿林［25］采用Monte Carlo法，根据组合柱轴压承载力公式，对型钢-钢管混凝土短柱进行了可靠性分析。结果表明：可靠指标随着可变荷载组合类型的改变而改变，随着混凝强度等级的提高而增大，随着钢管壁厚的增大而减小，随着荷载效应比的增大而先增加后降低。

2014年，查晓雄［26］通过确立配筋钢管混凝土构件的材料设计指标，对构件在轴拉和轴压作用下进行了可靠度分析。结果表明延性构件的目标可靠度为3.2。

5.2 空心钢管混凝土柱的可靠度研究现状

2007年，袁伟斌［27］采用一次二阶矩法，对各种受力状态下的离心钢管混凝土构件进行了可靠性分析，研究了混凝土强度等级、钢材变化、长细比、荷载比和活载类型对可靠度的影响。

2007年，钟善桐［28］提出直接由组成钢管混凝土构件的钢材和混凝土所占承载力的比例来确定钢管混凝土构件的组合可靠指标。根据构件的破坏性质，确定空心钢管混凝土构件的可靠指标为3.7。

2010年，王宏伟［29］考虑空心钢管混凝土中钢材和混凝土的共同工作性能，按照由组成构件的钢材和混凝土所占承载力的比例，计算出钢管混凝土构件组合可靠指标。并结合试验，确定了空心钢管混凝土轴心受压构件的组合可靠指标和强度折减系数。

2015年，孙小允［30］采用Monte Carlo法，分别计算了空心钢管混凝土构件的承载能力极限状态可靠度和正常使用极限状态可靠度。并研究了混凝土强度、钢材强度、含钢率和荷载效应比对空心钢管混凝土构件可靠度的影响。

6 总结与展望

可靠性分析需要大量的试验数据作为统计样本，国内规范和文献对钢管混凝土构件的承载能力、材料强度和几何尺寸的统计数据有限，难以进行高精度的数值分析。充分利用有限的试验数据，选择最合适的概率分布来对各种误差进行拟合，是钢管混凝土结构可靠性分析的关键。

目前国内结构可靠度的计算主要采用JC法。由于钢管混凝土结构承载力计算公式形式复杂，各变量之间存在相关性，采用JC法计算需要进行大量等效转换，过程复杂。计算机的发展和计算技术的提高解决了蒙特卡洛法计算量大的缺点，蒙特卡洛法可以回避承载力计算公式形式复杂的问题，进而提高钢管混凝土结构可靠分析的精度。

关于空心钢管混凝土结构可靠度的研究十分缺少，现存试验数据不足以进行各种误差的概率分布拟合。加上规范中对不同截面形式的实、空心钢管混凝土结构的承载力计算公式并不统一，增加了空心构件可靠性分析的难度。利用“钢管混凝土统一理论”，将实、空心构件统一起来研究其可靠度，是钢管混凝土结构可靠性分析的一种发展方向。●

［1］钟善桐.钢管混凝土统一理论——研究与应用［M］.北京：清华大学出版社，2006.

［2］卢德辉.圆、方形空心钢管混凝土柱抗震性能研究［D］［硕士学位论文］.广州大学，2012.

［3］GB50396-2014钢管混凝土结构技术规范［S］.

［4］李国强.工程结构荷载与可靠度设计原理［M］.北京：中国建筑工业出版社，2005.

［5］Freudenthal，A.M.The Safety of Structures［M］.ASCE.V.112，1947.

［6］A.H-S.Ang.Probability Concepts in Engineering Planning and Design［M］.New York:John Wiley&Sons，1975.

［7］Cornell C A.A Probability-based structural code［J］.ACIJ.1969，66（12）:974-985.

［8］B.Ellingwood.Development of a Probability Based Load Criterion for American National Standard A58，Building Code Requirements for Minimum Design Loads in Buildings and Other Structrues［J］.NBS SP-557，June，1980.

［9］C.C.Tung.Random Response of Highway Bridges to Vehicle Loads［J］.Jour.of the Engineering Mechanics Division，ASCE，Vol.93，No.EM5，Oct.1967.

［10］T.V.Galambos.Tentative Load and Resistance Factor Design Criteria for Steel Buildings［J］.Structural Division Research Report，No.18，Washington Univ.，St. Louis，Sept.，1973.

［11］Jame T.P.Yao.An Approach to Damage Assessment of Existing Structures［J］.Purde Univ.，Oct.，1979.

［12］D.Blockley.The Nature of Structural Design and

Safety［M］.Eills Horwood Ltd.，1973.

［13］Lind，N.C.Consistent Partial Safety Factors［J］. ASCE，V.97，No.ST6，June，1971.

［14］GBJ 68-1984建筑结构设计统一标准［S］.

［15］GB50153-1992工程结构可靠度设计统一标准［S］.

［16］GB50068-2001建筑结构可靠度设计统一标准［S］.

［17］陶忠，韩林海.钢管混凝土构件设计计算及可靠度分析［J］.工业建筑，2000，30（6）:1-6.

［18］覃亚伟，李惠强.钢管砼轴心受压柱的可靠性研究［J］.华中科技大学学报（城市科学版），2003，20（3）:62-64.

［19］肖国涛，廖绍怀.基于Matlab的Monte-Carlo法对钢管混凝土构件的可靠度分析［J］.建筑技术开发，2004，31（9）：46-48.［20］许成祥.钢管混凝土柱框架结构体系的抗震可靠度分析［J］.长江大学学报，2005，2（1）：84-87.

［21］余志武，贺飒飒.钢管混凝土短柱极限承载力可靠度分析［J］.工程力学，2006，23（11）:139-144.

［22］蔡小萍.基于Matlab优化工具箱对钢管混凝土轴压短柱的可靠度分析［J］.南昌大学学报，2006，28（9）:303-306.

［23］李飞.钢管混凝土柱的可靠度与优化分析［D］［硕士学位论文］.西安理工大学，2008.

［24］周圣斌.钢管混凝土柱极限承载力可靠度校准分析［J］.建筑科学，2009，25（3）:78-81.

［25］肖阿林，何益斌，黄频.型钢-钢管混凝土短柱轴压承载力可靠度分析［J］.建筑结构学报，2010，31（8）：29-35.

［26］査晓雄，张晓伟，等.钢管混凝土构件可靠度分析［J］.施工技术，2014，43（增刊）:367-370.

［27］袁伟斌，金伟良.离心钢管混凝土构件设计的可靠度［J］.哈尔滨工业大学学报，2007，39（8）:38-43.

［28］钟善桐.钢管混凝土构件组合可靠度的分析［J］.哈尔滨工业大学学报，2007，39（8）（增刊2）：63-69.

［29］王宏伟，钟善桐.基于可靠度指标的空心钢管混凝土轴心受压构件设计［J］.工程力学，2010，27（增刊1）:250-253.

［30］孙小允.圆空心钢管混凝土轴压短柱可靠度分析［D］［硕士学位论文］.广州大学，2015.