基于包络相关法的特定辐射源识别

章 艳

(南京信息职业技术学院，南京 210023)



基于包络相关法的特定辐射源识别

章 艳

(南京信息职业技术学院，南京 210023)

研究了接收信号为常规信号条件下，基于包络相关法的特定辐射源识别算法。对分选过的属于同一型号的不同个体雷达信号，先将观测信号进行消噪滤波，以提高信噪比，然后对处理后的观测信号进行包络提取，并计算其与标准模态包络的相关系数，在此基础上构造检验统计量，实现特定辐射源识别。计算机仿真实验表明：当被识别信号的互相关系数为0.99左右、信噪比为0 dB时，平均识别正确率达96%。

特定辐射源识别；离散傅里叶变换；相关系数

0 引 言

在电子侦察信号处理中,需要对电子侦察接收机所接收到的来自各种不同型号雷达的辐射源加以区分,以实现对不同个体雷达识别为目标的特定辐射源识别，这已成为众多学者研究的热点问题[1]。由于特定辐射源之间的一般特征(如五大参数)基本相同,因此要进行特定辐射源识别，显然不能只依靠传统参数，而需通过寻找具有唯一性的代表性特征，如无意调制特征、晶振稳定度，等。这些特征与雷达的制造工艺的不一致性有关，这些特征是由于雷达的主要部件在制造过程中的随机因素所致,比如脉冲调制器、磁控管等参数的分散性、频率源的相位噪声，等。

从目前发表的相关文献来看,特定辐射源识别方法可大致分为两类：一类是时域法[2]，以包络特征居多;另一类是变换域法，主要通过小波变换(以其各个尺度下的小波系数作为识别依据)及HHT变换。

文献[3-4]提出了一种基于脉内参数的识别方法。该方法针对调幅及调相两类不同的调制样式，分别以解调后的包络特征(如上升及下降时间，顶降或上升角、下降角)及调频信号特征(如调频角，衰减线性，时频特性)作为识别依据,但该方法需要多脉冲积累才能进行有效识别。文献[5-6]将辐射源的寄生辐射作为识别依据,在微波测量的基础上，将测得的寄生分量频率集进行适当变换,用回归方法进行曲线和通过文献[5]中的式(3.2)、(3.3)分别提取表面场强S及曲线弧长L作为特征，进行识别,但没有给出性能分析。 文献[7]结合平滑滤波及复小波分解方法,以小波系数构建识别特征量，对同型号不同个体雷达进行识别，但该方法由于采用了平滑滤波方法，在实现滤波的同时，也带来了包络的失真，从而限制了其在低信噪比时的识别性能。上述方法属于第一类方法。

第二类方法，文献[8]利用小波变换方法，在有理分辩率基函数下进分解，以分解系数作为特征，实现特定辐射源识别。文献[9]基于HHT变换,定义了能量熵、第一阶及第二阶颜色矩作为识别特征完成特定辐射源识别。

考虑到电子侦察的低噪比、无先验知识的特定条件，加之同一型号雷达之间的差异微细，因此更多地关注于如何在低信噪比、先验知识贫乏的条件下提高特征参数的精度，而尽可能利用单个脉冲进行识别正是解决这一问题的方向之一。本文研究针对特定辐射源识别问题，提出一种将频域滤波与包络特征提取相结合的个体雷达识别算法。仿真结果验证了本文算法的有效性。

1 观测信号的消噪处理

1.1 设观测信号模型为

x(n)=a(n)exp[j(2πf0nΔt+φ0)]+w(n)

0≤n≤N-1

(1)

式中:a(n)为包络函数；f0为信号的载频；φ0为初相位；Δt为采样间隔；N=T/Δt为采样点数；w(n)为零均值平稳复白高斯噪声，方差为2σ2。

精确的包络提取是进行特定辐射源识别的前提，故必须对接收信号进行消噪滤波，以提高包络提取的精度。现有的噪声消除方法主要有平滑滤波[8]、小波消噪[10]、基于EMD分解的噪声消除[11]。平滑滤波方法是基于噪声的不相关及信号的强相关性，通过若干点相加取平均的方法进行消噪。小波消噪及基于EMD分解的噪声消除的基本思想是通过分解，在一定的阀值下，去掉几层高频分量，但运算量较大，且最优分解层数较难确定。考虑到电子侦察信号接收机在设计时，一般系统的带宽较宽[12]，以便进行宽频域搜索，而信号带宽相对而言变窄，因此，可利用DFT方法进行滤波，以提高处理性能。本文给出一种基于频域处理的滤波算法，描述如下：

1) 对接收信号作N点DFT，得到X(k)=DFT[x(n)]；

2) 定义滤波器的离散傅里叶变换为

(2)

式中：k0为|X(k)|的最大谱线位置；δ为滤波带宽，与包络的频带宽度及信噪比均有关；

3)令X′(k)=H(k)X(k)，然后对X′(k)作N点IDFT，得x′(n)=IDFT(X′(k))。

1.2 滤波性能分析

(3)

若定义信噪比

(4)

式中：A为信号包络的平均值。则滤波后的信噪比SNR′为

(5)

所以，滤波后的信噪比增加了约N/2δ倍，(一般N>>2δ)，处理信噪比得到显著提高，对后续包络细微特征提取提供了保障。图1a)、图1b)所示分别为某信号包络在SNR=6 dB时，消噪滤波前后包络波形的对比。由图可见，信号包络经滤波后变得平缓，信噪比提高显著。这样接收信号经滤波后，可写为

x′(n)=a(n)exp[j(2πf0nΔt+φ0)]+w′(n)

0≤n≤N-1

(6)

图1 噪声中的信号包络与消噪后的信号包络波形

2 识别算法

2.1 同型号不同个体雷达的差异度量

假设数据库中的有型号相同但不同个体雷达标准模态信号S1，S2，其归一化后包络分别为A1=(a10,a11,a12,…,a1,N-1),A2=(a20,a21,a22,…,a2,N-1)，二者的互相关系数rA1A2定义为

(7)

2.2 算法描述

经滤波重构信号，则前述的特定辐射源识别可建模为如下二元假设检验问题

(8)

1)对x′(n)提取包络Z(n)，

Z(n)=abs(x′(n))=(z0,z1,z2,…,zN-1)

(9)

2) 分别计算Z(n)与两个标准模态的相关系数rA1Z,rA2,Z

(10)

3) 对于一定的门限VT，构造检验统计量

G=rA1Z-rA2Z

(11)

4) 若G≥VT，则H1成立，即接收信号的包络S1，否则属于S2。

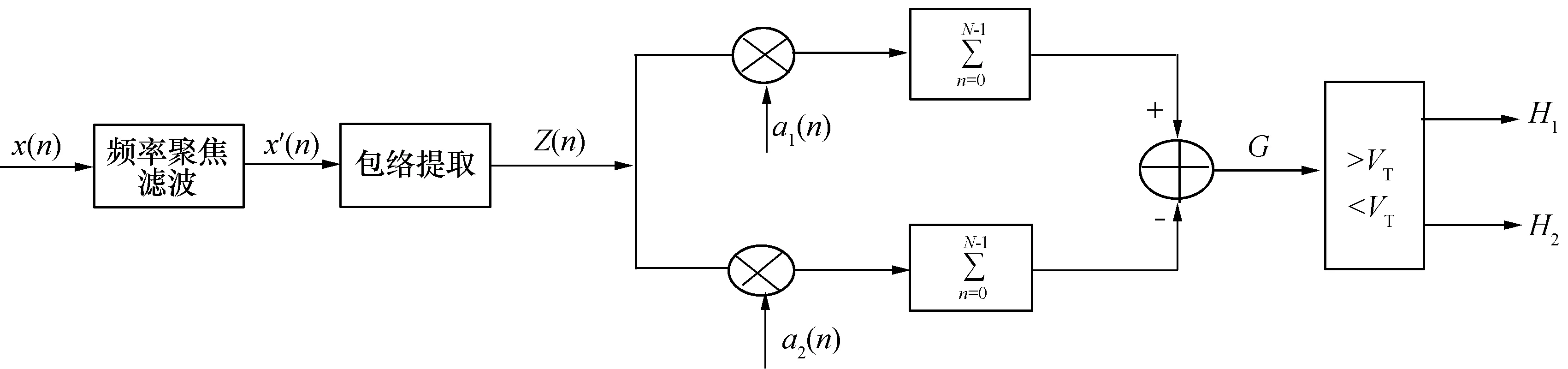
图2 本文算法的计算框图

3 仿真实例

仿真中接收信号为如式(1)所定义，设定两个来自不同个体的信号包络作为标准模态信号，其相关系数设定为

rA1A2={0.93，0.967 3,0.976 5,0.988 7,

0.993 2,0.998 9 }

(12)

接收信噪比定义由式(4)给出，从-6 dB～9 dB变化，步长为3 dB。仿真中，分别对来自两个不同个体的信号包络各进行100次仿真，每个信噪比下分别以两个标准模态为包络函数，按式(1)模型并加上高斯噪声构建待识接收信号。接收信号的载频波率设定为f0=30 MHz，脉宽为T=10.24 μs，样本数N=1 024，采样间隔Δt=T/N=10-8s。

3.1 滤波带宽的选取

滤波带宽δ的选取是进行精确包络的提取的关键，主要跟DFT的点数、包络的带宽及输入信噪比有关。由此进行参数建模较为复杂。下面介绍一个简单的方法，在一定信噪比下，取不同的δ(一般δ∈[5,20])，进行多次重复，计算滤波后包络与已知包络的互相关系数的平均值，取使之达到最大的δ的值作为经验最佳值δopt。某包络在不同信噪比条件下，经过100次重复所得最佳滤波带宽的仿真结果如表1所示。其中，r1是在最佳滤波带宽下的互相关系数，r2为滤波前的互相关系数。

表1 不同信噪比下的最佳滤波带宽

由表1可知,通过滤波后的包络与真实包络的相关性增加较大,信噪声比大于0 dB时,达到0.99,滤波效果佳。在适度的信噪比范围内，可以取一个经验值作为统一的滤波带宽。本文取δ=11进行仿真。

3.2 性能分析

由表2可知,本算法的识别性能随着信噪比的增加而下降，同时也受相关系数的大小的影响。信噪比不变时，相关系数越接近1，说明两个标准模态之类的差别越小，从而识别难度增加，识别性能也随之下降。反之，当标准模态间的相关系数小时，说明二者之间差别较大，易于区分，其识别性能也随之变好。如表2所示，当相关系数r=0.93时，0 dB时平均识别正确率就达100%，而当相关系数为r=0.993 2，平均识别正确率为96%。当标准模态间的相关系数不变时，信噪比越小，识别特征量的可区分度也随之下降，从而导致识别性能下降。如表2所示，当标准模态的互相关系数达0.993 2时，信噪比0 dB条件下，其平均识别正确率可达96%，而当信噪比为3 dB时，平均识别正确率达100%；当标准模态的互相关系数为0.999 2时，信噪比6 dB时，平均识别正确率达90%；当标准模态的互相关系数为大于0.993 2时，由于标准模态的差别变小，在低信噪比条件下时，性能变差。

表2 常规信号在不同信噪比、不同标准模态相关系数下的识别性能

SNR/dB-6-30369r=0.93009598.0100.0100.0100100r=0.96737194.5100.0100.0100100r=0.97656397.5100.0100.0100100r=0.98864789.5100.0100.0100100r=0.99324282.096.099.0100100r=0.99894172.573.586.59398r=0.9992246772.5899098r=0.99963656.56773.578.589.5

4 结束语

本文研究了一种基于信号包络特征分析的特定辐射源识别算法。为了提高处理性能，先对信号进行频率滤波处理，再提取包络，利于精细处理。文中以常规信号为例进行了仿真分析，结果表明该算法在两个标准模态差异较小、较低信噪比条件下，仍具有较好的识别性能。此外，本算法用提取包络作为识别特征，易于扩展于其他存在脉内调制时的特定辐射源识别(如线性调频信号，相位编码信号，经过适当变换均可转化为常规信号)。

[1] LANGLEY L E.Specific emitter identification (SEI) and classical parameter fusion technology[C]//WESCON 93 Conference Record.[S.l.]:IEEE Press,1993:377-381.

[2] 王宏伟，赵国庆，王玉军.基于脉冲包络前沿高阶矩特征的辐射源个体识别[J].现代雷达,2010,32(10)：42-45.

WANG Hongwei,ZHAO Guoqing,WANG Yujun.Specific emitter identification based on higher order moment of the envelope's front edge[J].Modern Radar,2010,32(10):42-45.

[3] KAWALEC A,OWCZAREK R,DUDCZYK J.Data modeling and simulation applied to radar signal recognition[J].Molecular and Quantum Acoustics,2005(26):165-172.

[4] OWCZAREK R.Specific radar identification based on measurement of signal features in the time domain[D].Warsaw:Military University of Technology,2004.

[5] DUDCZYK J,MATUSZEWSKI J,WNUK M.Applying the radiated emission to the specific emitter identification[J].Inernational Conference on Microwaves,2004,5(1):37-47.

[6] DUDCIYK J.Applying the radiated emission to the radio-electeronic devices identification[D].Warsaw:Military University of Technology,2004.

[7] 张国柱,黄可生,姜文利,等，基于信号包络的辐射源细微特征提取方法[J].系统工程与电子技术，2006,28(6):795-797.ZHANG Guozhu,HUANG Kesheng,JIANG Wenli,et al.Emitter feature extract method based on signal envelope[J].Systems Engineering and Electronics,2006,28(6):795-797.

[8] BRUCE P.Anderson the rational resolution analysis:a generalization of multiresolution analyses with application to the specific emitter identification problem[M].New York:Storming Media,1997.

[9] ZHANG J,WANG F,DOBRE O A,et al.Specific emitter identification via hilbert-huang transform in single-hop and relaying scenarios[J].IEEE Transactions on Information Forensics & Security,2016,11(6):1-1.

[10] BOUDRAA A O,CEXUS J C,SAIDI Z.EMD-based signal noise reduction[J].Proceedings of World Aeademy of Science Engineering & Technology,2005,1(1):93-96.

[11] JANSEN M.Noise reduction by wavelet thresholding[M].New York:Springer-Verlag,2001.

[12] ROBERT N,DONOUGH M,WHALEN A D.Detection of signals in noise[M].2nd ed.New York:Academic Press,1995.

章 艳 女，1979年生，本科，讲师。研究方向为信号处理、计算机技术。

Specific Radar Emitter Recognition Based on Correlation Coefficient of the Envelope Methods

ZHANG Yan

(Nanjing College of Information Technology,Nanjing 210023,China)

In this paper，correlation coefficient of envelope on specific emitter recognition is discussed when the received radar signal is a normal type.In this approach,in order to determine which specific radar generated the intercepted signals belong to the same kind after classified ,received signals are firstly filtered by DFT to reduce the noise ,then the envelope of the processed signals are extracted.Computer simulation results show that the method is able to identify the two specific radar emitters with an accuracy rate of 96% when the correlation is about 0.99,and the input SNR is 0 dB.

specific emitter recognition; DFT; correlation coefficient

��处理·

10.16592/j.cnki.1004-7859.2016.10.010

章艳 Email：zhangyan.zk@njcit.cn

2016-07-07

2016-09-17

TN957

A

1004-7859(2016)10-0039-03