飞行高度对雷达对海性能影响性分析评估

梁 浩，李国刚，徐艳国

(南京电子技术研究所,南京 210039)



飞行高度对雷达对海性能影响性分析评估

梁 浩，李国刚，徐艳国

(南京电子技术研究所,南京 210039)

回顾了点目标和面杂波的经典雷达方程和接收机噪声基本原理，介绍了三种经典海杂波单位面积反向散射率经验模型。使用经验模型分析了不同飞行高度、特定海情条件海杂波分布特性。使用实际试飞数据印证了实录机载海杂波与经验模型的趋势一致性。结合海杂波背景中目标检测的特点，提出了一种快速评估飞行高度对海杂波背景下目标检测的影响性分析评估方法。最终给出了机载海面监视雷达使用高度的选择建议。

海面监视雷达；海杂波；飞行高度；海情海况

0 引 言

机载海面监视雷达目标检测面临的主要背景是海杂波，海杂波特性与诸多因素相关，包括：海情海况、风速、风向、雷达照射方向、浪涌传播方向、载机飞行高度等[1-2]。上述因素中，对载机飞行高度影响海杂波的关注较少，然而，其影响又客观存在，不容忽视。如何在相应海情海况和风向条件下，应用本文提出的快速分析评估方法，在特定海情条件下，选择合适的飞行高度，获得最佳目标检测效果，是本文研究和分析的重点内容。

1 海面目标检测原理

由于实际工作环境中，海情海况变化莫测，遇到完全风平浪静的理想海面概率较低，海面回波(海杂波)广泛存在。海面监视雷达在海面目标检测过程中，无法回避海杂波存在性问题。

随着探测距离的延伸，海杂波将逐渐衰减，并最终淹没在接收机噪声背景中。由于检测背景不同，因此，必须将目标检测的信号处理分为杂波区和噪声区进行考虑。

在海杂波背景中，信号处理从回波中检测目标需要对抗海杂波回波，关注指标应为信杂比(SCR)，即目标回波功率与杂波回波功率的差异程度。

在纯噪声背景中，信号处理从回波中检测目标需要对抗接收机噪声，关注指标为信噪比(SNR)，即目标回波功率与接收机背景噪声功率的差异程度。

1.1 点目标雷达方程

点目标雷达回波方程，给出了特定距离确定雷达反向散射截面积(RCS)的点目标回波功率理论值的计算公式[3]

(1)

式中：Pr为雷达接收目标回波功率；Pt为雷达发射峰值功率；G为雷达天线增益；σT为目标平均RCS值；D为脉冲压缩比；λ为雷达工作波长；R为目标存在距离；Ls为各类系统损耗和传输损耗总和。

1.2 面杂波雷达方程

面杂波雷达回波方程给出了特定距离面杂波(地物杂波或海面杂波)的回波功率理论值计算公式[3]

(2)

式中：Pr为雷达接收面杂波回波功率；Pt为雷达发射峰值功率；G为雷达天线增益；c为光速；τ为脉冲压缩后脉冲时宽；θaz为方位波束宽度；σ0为单位面积反向散射因子；D为脉冲压缩比；λ为雷达工作波长；θel为雷达波束擦地角；R为杂波单元距离；Ls为各类系统损耗和传输损耗总和。

1.3 接收前端噪声功率

雷达接收机的射频前端的热噪声是系统噪声的重要组成部分，其功率理论计算公式[3]为

PN=k×T0×B×Fn

(3)

式中：k为玻耳兹曼常数；T0为基准温度290K；kT0=4×10-21W/Hz；B为接收机工作带宽；Fn为考虑非理想接收机(实际工程化接收机)所引入的额外噪声影响，引入的噪声系数。

可使用的简便计算公式[4]为

PN=-114+Fn+10lgB

(4)

式中：PN单位为dBm；B单位为MHz。

1.4 目标信杂比和信噪比

在系统处理能力可承载目标和虚警数量条件下，通过设定不同的检测门限(差异程度比较)，完成目标CFAR检测处理。

在杂波背景中，目标信杂比可表述为

SCR=PTr-PCr

(5)

式中：PTr为点目标回波功率，单位为dBm，可通过式(1)进行计算；PCr为海杂波回波功率，单位为dBm，可通过式(2)进行计算。

在噪声背景中，目标信噪比可表述为

SNR=PTr-PN

(6)

式中：PTr为点目标回波功率，单位为dBm，可通过式(2)进行计算；PN为接收机噪声背景功率，单位为dBm，可通过式(3)进行计算。

鉴于海杂波分布的拖尾特性，在信号检测过程中，通过设定适当的CFAR门限，抑制短时相关(2 ms左右)杂波虚警，容忍“海尖峰”长时相关(2 s左右)杂波虚警，再通过扫描间相关的处理方法对“海尖峰”类虚警进行抑制，具体实施方法可参考相关文献[5]。

2 海杂波单位面积反向散射率σ0建模

海杂波建模模型复杂，目前尚没有完整的海洋电磁学理论进行可靠支撑，已经获得较广泛认可的模型，都是基于大量实际回波数据的规律总结和参数提炼。本文计算采用了被广泛采纳认可的三种海杂波单位面积反射率σ0模型：GIT模型、TSC模型和HYB模型。这里没有选用SIT模型，因为该模型只给出了迎风和侧风向的海杂波σ0建模方法。

通过比较三者计算结果进行相互验证，最终以三者的均值作为参与系统理论计算的海杂波单位面积反射率σ0参考值，以期获得最贴近实际环境的结果，理论计算所使用的海情海况描述相关参数见表1。

表1 海情海况标准描述 m

2.1 GIT模型[6]

Georgia技术研究所建立了一个确定性、参数化的海杂波单位面积平均反向散射率模型，该模型包含擦地角、风速、与风速相关的平均浪高、雷达波束和风向夹角关系、雷达工作频率和收发极化形式在内的一系列相关参数。

GIT模型包括海面后向散射机制在内的多项理论模型为基础，结合引入经验因子而建立，是目前被广泛所接受描述海杂波单位面积平均反向散射率最好的模型之一。GIT模型由以下几个因素构成：

(1) 干涉因子AI

σφ=(14.4λ+5.5)φhav/λ

(7)

(8)

式中：λ为雷达波长；φ为波束擦地角；hav为平均浪高。

(2) 风向因子Au

Au=exp[0.2cosΨ(1-2.8φ)(λ+0.02)-0.4]

(9)

式中：Ψ为波束指向与风向间夹角。

(3) 风速因子Aw

qw=1.1/(λ+0.02)0.4

(10)

Aw=[1.94Vw/(1+Vw/15.4)]qw

(11)

式中：Vw为海面风速，若对于“充分发展”的海面，Vw和平均浪高hav间存在下述关系

(12)

对于工作频率在10 GHz以下的水平极化体制雷达，海杂波单位面积反射率σ0(单位：dBm2/m2)的GIT模型可描述为

σ0=10lg(3.9×10-6λφ0.4AIAuAw)

(13)

2.2 TSC模型[6]

TSC公司提供了一个可良好拟合Nathanson数据的模型。该模型与波束擦地角、Douglas海情海况等级、风向角度、雷达工作频率和收发极化形式相关。在TSC模型中，有效的风速和浪高直接使用Douglas海情海况等级计算推导获得。

在相对谨慎和保守的性能预测时，推荐使用TSC模型，因为相比GIT模型而言，TSC模型更加接近平均条件(注：TSC模型针对小擦地角评估准确性优于中、大擦地角条件)。

TSC模型由以下几个因素构成：

(1) 小擦地角因子GA

σz=0.115S1.95

(14)

σα=14.9φ(σz+0.25)/λ

(15)

(16)

式中：λ为雷达波长(单位：ft，1ft=0.304 8 m)；φ为擦地角(单位：rad)；S为海情海况等级。

(2) 风速因子Gw

Vw=6.2S0.8

(17)

Q=φ0.6

(18)

A1=(1+(λ/0.03)3)0.1

(19)

A2=(1+(λ/0.1)3)0.1

(20)

A3=(1+(λ/0.3)3)Q/3

(21)

A4=1+0.35Q

(22)

A=2.63A1/(A2A3A4)

(23)

Cw=[(Vw+4.0)/15]A

(24)

式中：Vw为海面风速(单位：节)。

(3) 方向因子Gu

B1=exp(-φ/0.17)

(25)

B2=(λ2+0.005)0.2

(26)

Gu=exp(0.3cosΨB1/B2)

(27)

式中：Ψ为波束指向与风向间夹角(单位：rad)。

对于水平极化体制雷达，海杂波单位面积反射率σ0(单位：m2/m2)的TSC模型可描述为

σ0=1.7×10-5φ0.5GuGwGA/(λ+0.05)1.8

(28)

2.3 HYB模型[6]

使用HYB模型估算海杂波平均单位面积方向散射率时，以5级海情、0.1°擦地角、垂直极化和迎风观测为参考基准值，对于海况等级、波束擦地角、极化方式和波束与风向夹角等变量，提供了约4 dB的动态调节范围。过渡擦地角取值源于GIT模型和Barton的分析结果。

HYB模型由以下几个因素构成：

(1) 参考反向散射率σ0(ref)

对于X波段的雷达，参考反向散射率σ0(ref)可描述为

σ0(ref)=24.4lg(f)-65.2

(29)

式中：f为雷达工作频率。

(2) 擦地角调节因子Kg

对于擦地角调节因子，定义参考擦地角φr(单位：°)和过渡擦地角φt(单位：°)

φr=0.1°

(30)

φt=arcsin(0.063 2λ/σh)

(31)

式中：σh为浪高均方根值，其与海情海况等级S间存在关系如下

σh=0.031S2

(32)

对于φr≤φt≤ 30°的情况，擦地角调节因子Kg可定义为

(33)

对于φr>φt的情况，擦地角调节因子Kg可定义为

(34)

(3) 海情海况调节因子Ks

Ks=5(S-5)

(35)

(4) 极化形式调节因子Kp

Kp=1.1ln(hav+0.015)-1.1lnλ-

1.3ln(φ/57.3+0.000 1)-9.7

(36)

式中：hav为平均浪高；λ为雷达工作波长。

海情海况等级S与平均浪高hav间存在如下关系

hav=0.08S2

(37)

(5) 风向调节因子Kd

Kd=[2+1.7lg(0.1/λ)](cosΨ-1)

(38)

式中：Ψ为相对于雷达波束照射方向的风向，将迎风照射时的风向角度定义为0°。

对于水平极化体制X波段雷达，海杂波单位面积反射率σ0的HYB模型可描述为

σ0=σ0(ref)+Kg+Ks+Kp+Kd

(39)

2.4 海杂波单位面积反射率σ0模型共性分析

通过对GIT模型、TSC模型和HYB模型进行仿真计算可以看出，本类经验性模型体现的共同特征包括：

(1) 海杂波平均单位面积反向散射率随海情海况等级、工作频率和擦地角的增加而增加；

(2) 在小擦地角条件下，海杂波平均单位面积反向散射率与擦地角的依赖关系更加明显；

(3) 海杂波平均单位面积反射率在迎风向最大、顺风向最小，中间角度基本平滑过渡。

3 载机飞行高度对海面目标探测影响性分析

通过上述分析可知，海杂波单位面积反向散射截面积与擦地角间存在明显的强相关关系。因此，载机飞行高度将直接影响海杂波存在的延伸距离，也同步影响着雷达的海面目标检测性能。

3.1 载机飞行高度与杂波间相关趋势分析

按表2所示参数进行仿真，其仿真结果如图1和图2所示。仿真结果使用极坐标显示，其中，半径表示相对强度；方位表示风向，以真北顺时针为参考，图中所绘曲线均经过海情250 m条件下的海杂波最小单位面积反射率σ0值归一化处理。

表2 仿真参数设置

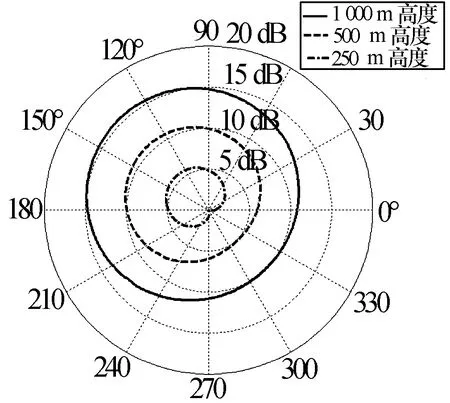
图1 东南风1级海情不同高度σ0仿真结果

图2 东南风3级海情不同高度的仿真结果

通过观察可以看出，在相同海情条件下，载机飞行高度越高，海杂波单位面积反射率越强；在相同高度条件下，海情等级约高，海杂波单位面积反射率越强；在水平极化天线设计中，迎风面海杂波单位面积反射率强，背风面海杂波单位面积反射率弱，其间角度均匀过渡。

图3和图4为试验雷达同一架次试飞的实际回波视频。从截图可以看出，在相同风向风速和海情海况条件下，随载机高度提升，杂波在迎风向上的延伸现象非常明显：在迎风向上，当载机高度为250 m左右时，海杂波延伸距离约25 km；当载机高度为1 000 m左右时，海杂波延伸距离扩展至50 km以上。

图3 东南风3级海情，250 m高度实际回波

图4 东南风3级海情，1 000 m高度实际回波

3.2 载机飞行高度对探测影响性分析方法

载机飞行高度对海面监视雷达海面目标探测性能影响性分析的步骤为：

(1) 设定仿真场景，包括：海洋环境参数、雷达设计参数、海面目标参数、载机飞行高度参数、目标检测参数；

(2) 海杂波单位面积反向散射率计算；

(3) 海面目标信杂比(SNR)计算；

(4) 海面目标信噪比(CNR)计算；

(5) 海杂波杂噪比(CSR)计算；

(6) 区分杂噪分界距离，当CSR> 1.0时，设定为杂波区，使用高门限检测策略，抑制虚警概率；当CSR≤1.0时，设定为噪声区，使用低门限检测策略，提高检测概率；

(7) 对不同海情海况、不同飞行高度、不同目标距离的条件，进行独立仿真，并通过绘图形式进行对比，判定目标检测性能。

3.3 载机飞行高度对探测影响性仿真结果

按表3所示参数进行设置，通过仿真可以看出，3级海情，载机飞行高度200 m条件下，保守估计的杂噪分界距离约35 km，在杂波区内，目标SCR> 7 dB，在噪声区内，目标SNR> 4 dB，因此，可获得不小于50 km的探测能力，如图5所示；载机飞行高度400 m条件下，保守估计的杂噪分界距离约44 km，在杂波区内，部分距离段目标SCR< 7 dB，在噪声区内，目标SCR> 4 dB，因此，雷达在杂波区15 km～44 km段会失去目标的稳定检测能力，如图6所示。

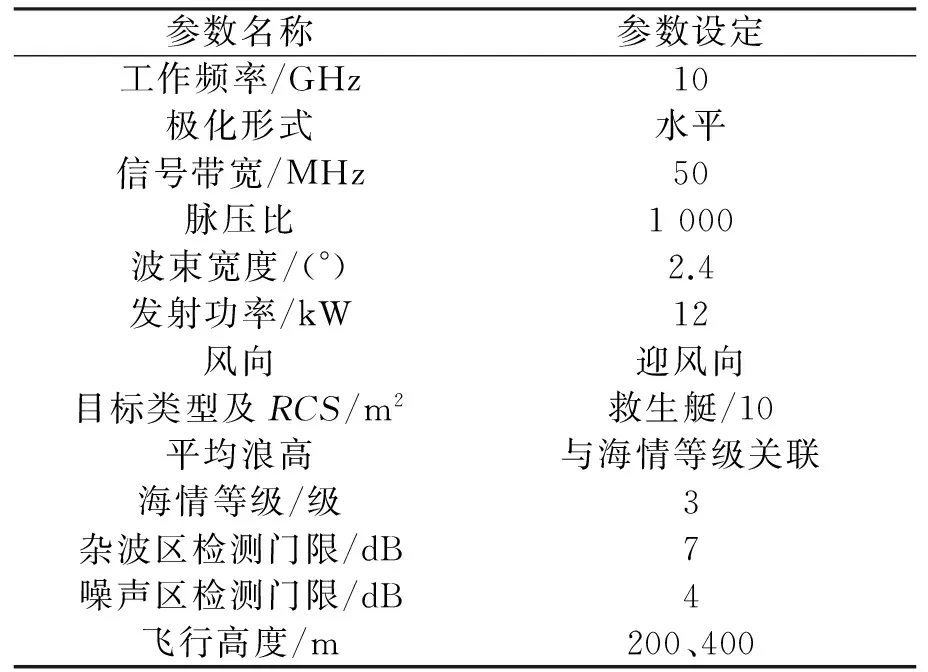
表3 仿真参数设置

图5 3级海情200 m高迎风探测10 m2目标能力

图6 3级海情400 m高迎风探测10 m2目标能力

4 结束语

本文利用三种典型海杂波单位面积反向散射率经验模型，完成海杂波简单建模。在此基础上，设定特定应用场景，提出一种评估机载雷达工作高度与海面目标检测能力影响性的定量分析评估方法。

通过使用该方法，可在不同海情海况条件下，结合作战任务，提前灵活规划航线高度，实现雷达对海探测性能最优化，对增进任务完成效果具有明确指导意义。

[1] WARD K D,BARKER C J,WATTS.Maritime surveillance radar.Part 1:Radar scattering from the ocean surface[J].IEEE Proceedings of Radar & Signal Processing,1990,137(2):51-62.

[2] WARD K D,BAKER C J,WATTS.Maritime surveillance radar.Part 2:Detection performance prediction in sea clutter[J].IEEE Proceedings of Radar & Signal Processing,1990,137(2):63-72.

[3] SKOLNIK M I.雷达手册[M].3版.北京:电子出版社,2010.

SKOLNIK M I.Radar handbook[M].3rd ed.Beijing:Publishing House of Electronics Industry,2010.

[4] 弋 稳.雷达接收机技术[M].北京:电子工业出版社,2005.

YI Wen.Radar receiver technology[M].Beijing:Publishing House of Electronics Industry,2005.

[5] SMITH J M,LOGAN R H.AN/APS-116 periscope detection radar[J].IEEE Transactions on Aerospace and Electronic Systems,1980,16(1):66-73.

[6] ANTIPOV I.Simulation of sea clutter returns[R].DSTO-TR-0679,AR-010-560.Salisbury South Australia:Electronic and Surveillance Research Laboratory,1998.

梁 浩 男，1983年生，硕士研究生。研究方向为直升机机载雷达电讯总体技术。

李国刚 男，1983年生，硕士研究生。研究方向为直升机机载雷达电讯总体技术。

徐艳国 男，1980年生，硕士研究生。研究方向为机载预警雷达电讯总体技术。

Analysis of the Influence of Flight Height on the Sea Surface Surveillance Radar Performance

LIANG Hao，LI Guogang，XU Yanguo

(Nanjing Research Institute of Electronics Technology,Nanjing 210039,China)

The radar equation of dot type target and surface clutter ,and the calculation of receiver front terminal noise power is reviewed，and then three normally used empirical models of mean sea clutter reflectivity are introduced in detail.The characteristic of sea clutter reflectivity under different flight height and specifically sea status is analyzed by means of introduced empirical models.The trend consistency between the practical radar sea clutter echo and empirical models is compared and verified.The characteristic of the target detection in sea clutter is taken into account,then a fast method to analysis and estimation the flight height influence on the radar performance is given.The suggestion of flight height selection to maximize the air-born surveillance radar performance is given in the end.

sea surface surveillance radar; sea clutter; flight height; sea status

��工程·

10.16592/j.cnki.1004-7859.2016.10.003

梁浩 Email：108754226@qq.com

2016-07-18

2016-09-20

TP971.1

A

1004-7859(2016)10-0008-05