利用高频天波返回散射反演电离层水平不均匀结构

冯静, 倪彬彬， 赵正予， 柳文， 蔚娜， 娄鹏

1 武汉大学电子信息学院， 武汉 430079 2 中国电波传播研究所， 青岛 266107



利用高频天波返回散射反演电离层水平不均匀结构

冯静1,2, 倪彬彬1， 赵正予1， 柳文2， 蔚娜2， 娄鹏2

1 武汉大学电子信息学院， 武汉 430079 2 中国电波传播研究所， 青岛 266107

高频天波返回散射探测作为重要的电离层探测手段，能够实现遥远区域电离层空间上的连续监测，探测获取的返回散射扫频电离图显示了探测频率-群路径-回波能量三者之间的关系.由于电离图包含了探测路径上的电离层状态信息，通过对其反演可以实时获取大面积范围的电离层参数.本文提出了一种基于解空间约束的返回散射前沿反演算法，能够重构电离层水平不均匀结构.针对反演非线性问题，采用Newton-Kontorovich方法进行求解，同时又引入了求解不适定问题的Tikhonov正则化方法，有益于解的稳定性和唯一性.利用模拟数据和实测数据分别对本文建立的算法进行了验证，并与Fridman和Fridman于1994年提出的反演方法进行了对比.结果表明，本文算法反演结果稳定，对返回散射前沿判读误差不敏感，与Fridman和Fridman 1994年方法相比，本文方法对电离层局部精细结构反演更加准确，具有较高的反演精度.本文提出的算法不但能够反演白天和夜间这种电离层较平稳时期的电离层状态，而且对于日出/日落时段等电子浓度分布变化较快情形下的电离层，也有很好的反演效果，表明了该算法在处理复杂多变的实际探测的返回散射电离图中的应用价值.

返回散射； 电离图； 电离层； 反演； 重构； 不均匀

1 引言

目前基于地面的电离层探测手段主要有垂直探测、斜向探测和返回散射探测.垂直探测能够获取垂测站上空电离层电子浓度信息，就获取单个地点上空电子浓度垂直剖面信息而言，垂直探测是三种探测手段中最直接、最准确的.斜向探测可以实现点对点固定地面距离的电离层探测，通过对斜向探测结果反演只能获取该距离对应的电离层反射区域信息.返回散射探测具有探测距离远、覆盖范围广的特点，能实时探测大面积范围电离层参数，是远区电离层信息的唯一来源，这是返回散射探测相比垂直探测和斜向探测来说最大的优势，对于某些无法布置垂直探测和斜向探测的区域(例如海洋、境外)，返回散射探测更有着不可替代的作用.Croft认为，要得到大面积电离层电波传播特性的整体评估，最有效的技术是返回散射探测(Croft, 1972).

利用返回散射探测系统进行固定方位的扫频探测可以获得探测频率-群路径-回波能量的三维图形，称为高频返回散射电离图.返回散射电离图包含了探测方向上的电离层介质和地面(海洋表面)介质的信息，根据探测到的电离图反推这些介质的特性就称为电离图反演(熊年禄等, 1999).由于电离层的时间聚焦和球形聚焦等效应，电离图上有着较清晰、陡峭的前沿(也称最小群时延)，一般能够准确判读.返回散射前沿除了受电离层电子浓度分布影响之外，几乎不受任何其他因素(如天线波束、地面特性等)的影响.而返回散射电离图的其他信息，比如后沿、回波能量等，除了电离层之外，还与发射功率、天线增益、吸收损耗、接收机灵敏度、地面特性等众多条件有关.因此，返回散射前沿被广泛用来进行电离层的反演研究.

不少学者已经致力于利用返回散射电离图反演电离层参数的研究，目前返回散射电离图的反演大致可以归纳为如下几类：(1) 基于迭代的拟合算法.首先是Rao(1974)利用返回散射电离图前沿任意三组(p′,f)数据反演准抛物模型的三个参数，随后，Rao(1975)提出了一种利用返回散射电离图离散散射源回波描迹反演电离层参数和散射源地面距离的方法.这两种反演算法都假设电离层球形对称，不考虑地磁场的影响，并且都是反演单层准抛物模型参数.DuBroff等(1979)将这种反演算法推广到电离层非球形对称的情况，假设了一个简单的梯度电离层模型，反演包括准抛物模型的3个参数及其梯度共6个参数.Norman(2003)将Rao的三组(p′,f)数据增加到多组，通过一种广义逆矩阵反演算法改善了Rao算法的不适定性，并且将这种反演算法推广到多层电离层的情况.(2) 引入求解不适定问题的理论与方法以解决返回散射电离图反演不稳定性问题.Chuang和Yeh(1977)利用地球物理反演中发展起来的BG理论建立了斜向探测和返回散射探测反演模型，并用简单模型的垂测反演结果验证了该方法的有效性.Fridman和Fridman(1994)以返回散射发射站处垂直探测得到的电离层电子浓度剖面和返回散射前沿作为输入，利用求解非线性问题的Newton-Kontorovich方法和线性不适定问题的Tikhonov正则化方法，反演电离层电子浓度的二维分布，获得电离层的水平不均匀结构(以下称该方法为Fridman 1994算法).该方法还被推广到反演电离层三维电子浓度分布(Fridman，1998；Fridman和Nickisch，2001；Fridman等，2009，2012).遗传算法是近些年来发展起来的一种高效的非线性全局优化算法，也有学者利用遗传算法来进行返回散射电离图的反演(谢树果，2001；Benito等，2008b).宋君等(2011)使用模拟退火方法对返回散射电离图前沿进行了反演，但是该方法只适用于电离层较平稳时期.Zhu等(2015)提出了基于模拟退火算法和IRI模型的返回散射前沿反演方法，能够得到F层二维电子浓度剖面.(3)基于返回散射前沿以外的信息进行反演.Dyson(1991)提出了一种利用返回散射电离图前沿和后沿相结合反演电离层剖面参数的方法.事实上，从理论计算上确定后沿是相当困难的，因此这不是一种令人满意的反演算法.此外，还有仰角扫描的返回散射电离图反演(Caratori和Goutelard，1997；Landeau等，1997；Jacquet等，2001；Norman和Dyson，2006；Benito等，2008a)，这要求返回散射探测的收发天线是可以仰角扫描的.

本文提出了一种利用返回散射电离图前沿反演电离层参数的新方法.不同于传统反演方法采用全频段反演的方式，本文基于解空间约束的思想，提出了频段递增逐步逼近反演算法，对解空间做出了合理限制.为了保证解的唯一性和稳定性，又引入了求解非线性问题的Newton-Kontorovich方法和求解线性不适定问题的Tikhonov正则化方法.本文建立的算法反演精度高，稳健性强，对返回散射前沿判读误差不敏感，能够提供返回散射探测方向上远至2000 km地面距离的二维电子浓度分布，较好地反映电离层水平方向的不均匀结构.文章的第二部分介绍反演算法的具体求解过程；第三部分利用水平不均匀电离层模型数据和实际探测的高频返回散射电离图对算法进行验证及统计，并给出了算法在电离层反演中的具体应用实例；第四部分是本文的结论.

2 反演算法

2.1 反演基本原理

基于此，我们提出了频段递增逐步逼近反演算法，即将返回散射探测频率划分为若干个频段，每一次反演使用的频段都在上一次反演使用的频段基础上增加一个频段，并且反演的初始电子浓度剖面取值为上一次的反演结果，对解空间做出限制.这样既可以避免确定不同频率区间反演结果的分界点以及随后需要考虑的连续性和光滑性问题，又可以很好地利用先验信息对解做出约束，逐步逼近真实解，提高反演精度.与传统的使用全频段工作频率的最小群时延数据反演电离层的方法相比，频率递增逐步逼近反演不仅能够看到电离层的“概貌”，还能看到电离层的“细节”，起到了“显微镜”的作用，具有更高的反演精度.

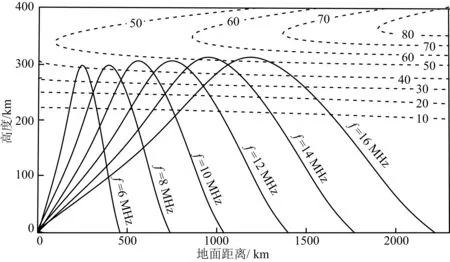
图1 不同频率形成最小群时延的射线轨迹示意图(虚线表示等离子体频率等值线，单位0.1 MHz)Fig.1 Ray tracks of the leading edge formed by different operating frequencies (The dotted line indicates the plasma frequency contour, the unit 0.1 MHz)

2.2 电离层模型

相对于整幅返回散射电离图而言，返回散射前沿只提供了探测路径上电离层的单一维度信息，用以反演全部的电离层结构是不充分的(Coleman，1998).为了克服这个问题，Fridman O V和Fridman S V(1994)建立了两种能够反映电离层水平不均匀结构的实用二维电离层模型，分别是水平梯度为常数的电子浓度模型和垂直剖面形状不变的电子浓度模型，它们都对实际电离层做了简化近似，都有一定的适用条件.前者适用于平静状态下电离层，后者更适合描述突变的、不规则的或者水平变化不单一的电离层结构.实际应用中，后者描述的电离层模型较前者更加适用，因此本文使用第二种电离层模型.

垂直剖面形状不变的电离层模型的数学表达式为

(1)

其中h表示高度，x表示地面距离，N0(h)表示初始的电子浓度剖面，u(x)表示不同地面距离x处电子浓度剖面相对于N0(h)改变的比例因子.N0(h)是已知的，u(x)是待求函数，一旦求解出u(x)，代入(1)式便可求得二维电子浓度分布N(h,x).

2.3 反演模型

利用返回散射前沿反演得到2.2节描述的二维电子浓度剖面需要求解下列第一类Fredholm积分方程：

(2)

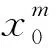
本文中的核函数采用Fridman和Fridman(1994)推导的计算公式：

(3)

其中，

上式中，fP表示等离子体频率；S=sinβ，β表示射线的出射角，即射线传播方向与垂直方向的夹角，有Sm=sinβm，其中βm表示返回散射前沿对应的射线出射角；RE表示地球半径；下标“0”表示均匀电离层模型下的参量，上标“m”表示最小群时延对应的参量.

由于返回散射电离图反演属于不适定问题，这里采用Tikhonov正则化方法进行求解，即利用光滑性对解做出限制，以保证解是最优且唯一.

(4)

其中

(5)

(6)

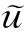
(7)

取得极小值的uα，这里α称为正则化参数，α>0.α越大，稳定化泛函Ω[u]在(7)式中的权重越大，得到的解uα也越光滑.但如果α取值太大，则会使解过分光滑而偏离真实解.最优正则化参数是使不等式(4)取得等号的α值.

2.4 反演的实现

本节主要介绍本文提出的反演算法的实现方法和步骤.

(1) 首先建立我们感兴趣区域的电离层电子浓度网格.在返回散射探测方位上，按照地面距离和高度分别划分网格，如图2所示.

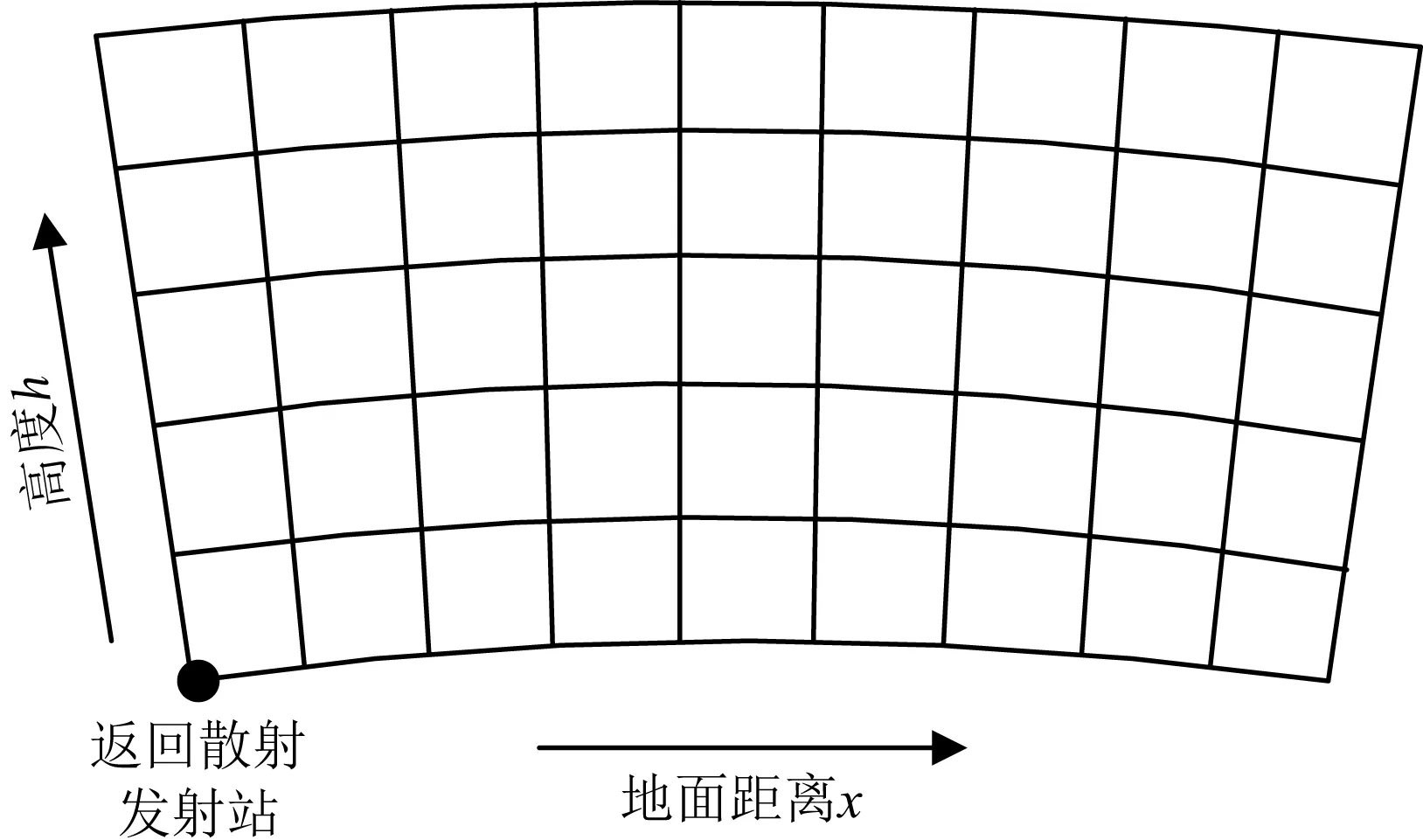
图2 二维电子浓度网格划分示意图Fig.2 Scheme of division of two-dimensional electron density grids

(2) 准备反演算法的输入，包括

① 实测的返回散射前沿G实测(f)；

② 返回散射发射站上空的电子浓度剖面N0(h)；

③ 将实测前沿G实测(f)对应的探测频率范围[fa,fb]划分为n个频段，每一频段的长度记为Δfi(i=1,2,…,n)，获取频率范围[fa,fa+Δf1]，[fa,fa+Δf1+Δf2]，…，[fa,fa+Δf1+Δf2+…+Δfn]=[fa,fb]对应的实测前沿的测量误差先验值δ1，δ2，…，δn，一般有δ1≤δ2≤…≤δn.

其中②利用发射站的垂测电离图反演得到.

(3) 首先利用频率范围[fa,fa+Δf1]的实测前沿数据G实测([fa,fa+Δf1])进行反演.由于反演问题(2)式一般是非线性的，这里采用求解非线性问题的Newton-Kontorovich方法进行迭代求解.具体步骤如下：

(I) 初始二维电子浓度剖面认为是水平均匀的，即图2中的电子浓度网格每一地面距离上空的电子浓度剖面都等同于返回散射发射站处的电子浓度剖面N0(h)，则有N(h,x)=N0(h).在此电离层模型下，利用柳文等(2008)发展的电离层短波数字三维射线追踪技术合成频率范围[fa,fa+Δf1]的理论前沿G理论([fa,fa+Δf1]).

(II) 使用符号‖‖表示均方根，定义理论前沿值与实测前沿值之间的均方根误差为

‖G理论(f)-G实测(f)‖=

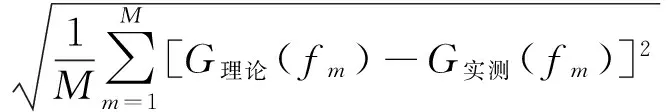
(8)其中M表示参与反演的前沿点个数.

如果下列条件满足

‖G理论([fa,fa+Δf1])-G实测([fa,fa+Δf1])‖

≤δ1,

(9)

则认为第(3)步的步骤(I)中的初始电子浓度剖面就是反演问题的最优解，否则进行下面的迭代过程.

(III) 求解频率范围[fa,fa+Δf1]的前沿数据对应(2)式的反演问题.

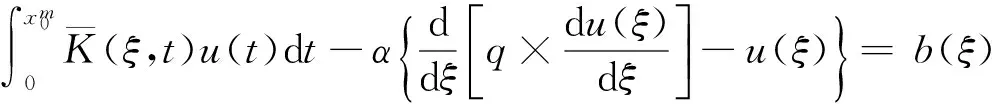
(10)满足边界条件

(11)

其中

这里，f1=fa，f2=fa+Δf1，G实测(f)=G实测([fa,fa+Δf1])，G理论(f)=G理论([fa,fa+Δf1]).

上述问题中，u是我们待求的未知函数；K是已知核函数，按照(3)式描述的方法计算；参数q一般需要满足条件q≥L2，其中L表示预期的电子浓度水平变化尺度典型值，考虑到中纬地区电离层水平不均匀性的典型尺度通常为上千千米量级或者更大，因此这里取值q=106km2.需要说明的是，虽然参数q的选择很重要，但只要它在一定范围内取值，反演结果对它是不敏感的.

由于我们引进了电子浓度网格，可以将上述问题表达式离散化，采用数值方法进行求解，离散化形式如下：

=bk，k=1,…,v

(12)

满足边界条件

(13)

其中

假设网格是均匀划分的，v代表地面距离网格个数，w代表探测频率个数，d表示地面距离网格的宽度，s表示探测频率步进.

固定正则化参数α的值，利用Cholesky分解法求解上述v个方程可以得到v个未知数的解uαk(k=1,…,v)，这是uα(x)的离散化形式.所有满足(4)式的α中的最大值称为最优正则化参数αd，它对应的解uαd(x)称为正则化解，也就是我们要求的解.将uαd(x)代入到(1)式，便得到反演后的电子浓度剖面N(h,x).

(IV) 在新的电子浓度剖面N(h,x)下，运用射线追踪技术合成频率范围[fa,fa+Δf1]的理论前沿G理论([fa,fa+Δf1])，将其代入(9)式，如果满足条件，则N(h,x)就是反演问题的最优解，记为N1(h,x)(上标1表示第1个频率范围反演过程的参量，以下类同).该频段的反演过程结束.否则，转入第(3)步的步骤(III).

(4) 接着利用频率范围[fa,fa+Δf1+Δf2]的实测前沿数据G实测([fa,fa+Δf1+Δf2])进行反演，其反演方法与第(3)步相同，只不过需将第(3)步的步骤(I)中涉及的初始二维电子浓度剖面取值成N1(h,x)，即上一频率范围对应的前沿数据反演得到的电子浓度剖面.记该频率范围的反演结果为N2(h,x).

(5) 将频率范围按照第(2)步的步骤③划分的方法逐步增加，然后按照第(4)步描述的方法完成反演，经过n次反演(对应n个频率范围)，最终得到二维电子浓度剖面Nn(h,x)，即我们的最优反演结果.至此完成本文算法的全部反演工作.

3 反演结果与分析

3.1 模拟数据反演

本节基于仿真数据来检验本文提出的反演算法对水平不均匀电离层的反演能力，仿真分析的思路是：假设一定水平不均匀分布的电离层模型，本节考虑柳文等(2005)建立的电离层扰动模型，将该电离层模型看作真实的电离层，基于真实的电离层仿真得到真实的返回散射前沿，然后基于真实的返回散射前沿采用不同的反演算法反演电离层参量，将反演得到的参量与真实电离层参量进行比较来验证反演算法的有效性.

柳文等(2005)建立的电离层扰动模型具有如下形式：

(14)

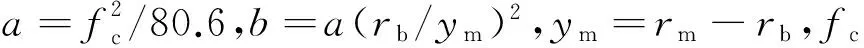
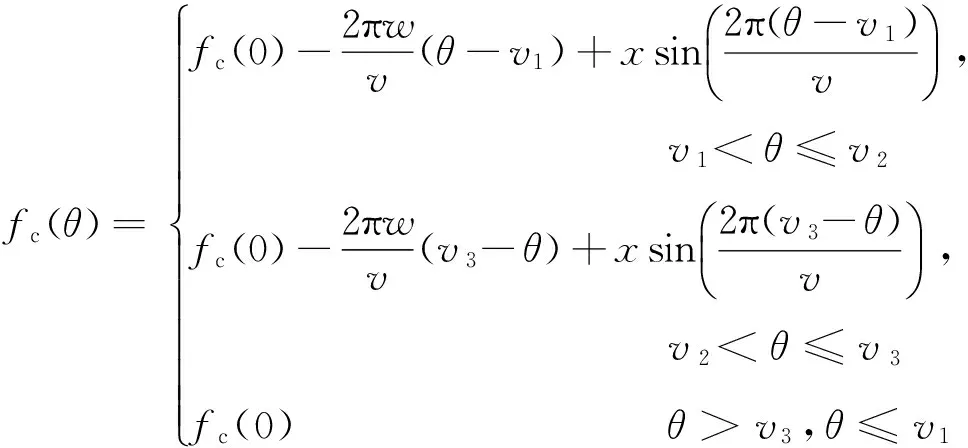
(15)式中，v1、v2、v3分别是由返回散射探测发射站算起的电离层扰动的前沿、中心和后沿的地心角位置(rad)，而且v=v2-v1=v3-v2，fc(0)是发射站上空电离层的临界频率，w为扰动区域临界频率波动的幅度(MHz/rad).

本文仿真设置的模型参数如下：fEc=2.5 MHz，rEb=6451 km，yEm=10 km，fFc=12.4 MHz，rFb=6571 km，yFm=130 km，扰动参数设置如下：v1=0.035 rad，v2=0.065 rad，v3=0.095 rad，wE=0.1 MHz/rad，wF=0.3 MHz/rad.

分别采用本文提出的算法和Fridman 1994算法进行反演，反演结果见图3.其中图3a给出了返回散射探测方位上距离发射站0～2000 km地面距离上空的F2层临界频率(foF2)分布情况的反演结果和真实结果，图3b给出了理论合成前沿与真实前沿的比较.

本例中，在利用射线追踪合成电离层扰动模型下的“实测”前沿时，加上了均方差为σd=20 km的随机误差，用来模拟测量误差.反演过程中，本文算法使用探测频率范围为5～28 MHz，划分为4个频段，参数设置分别为Δfi=5 MHz(i=1,2,3)，Δf4=8 MHz，δi=20 km(i=1,2,3,4).电子浓度网格的划分为40×400，即地面距离40个网格，对应0～2000 km，步进50 km；高度400个网格，对应0～400 km，步进1 km.从图3a可以看出，“实际”的电离层在距离发射站400 km左右出现了幅度较大的扰动，扰动区域约为350 km，最大扰动处foF2下降了1.9 MHz.Fridman 1994算法很好地捕捉到了扰动区域的位置，但是扰动区域的电子浓度反演得不够准确，最大扰动处的电子浓度比“实测”值低了0.65 MHz，而且在扰动后沿之后的地面距离上，foF2与实测值相比也有较大的误差.与Fridman 1994算法相比，本文提出的反演算法获得了更好的反演结果，最大扰动处的foF2与“实测”值仅相差0.2 MHz，扰动的后沿定位更加准确，绝大部分地面距离的电子浓度与“实测”值都吻合得较好.经过计算，本文算法和Fridman 1994算法反演地面距离0～2000 km上空foF2的均方根误差分别为0.11 MHz和0.26 MHz，说明整体上前者的反演精度也要高于后者.图3b给出了根据反演结果合成的返回散射前沿曲线，很明显，本文算法的合成结果优于Fridman 1994算法，在前沿出现抖动的区域(12～18 MHz)更加准确地反映了实际情况.3.2 实测数据反演

为了验证本文算法对实测返回散射电离图反演的正确性，我们利用中国电波传播研究所探测的实测数据进行了反演试验.经过大量实测数据验证，本文算法对实测数据的反演是有效的，反演结果稳定，具有较强的实用性.

整个试验探测系统包括1个返回散射探测系统、2个垂直探测系统(其中一个为准垂直探测系统，记为1号垂测站，另一个记为2号垂测站)和1个斜向探测系统，其中返回散射探测系统发射站和1号垂测站发射站位于A点，二者的接收站均位于与A点相距约100 km的B点，通过分别接收各自的发射信号可形成返回散射扫频电离图和B点处垂测扫频电离图；2号垂测站放置于返回散射探测方位上距离B点1000 km处的C点，可以得到C点处垂测扫频电离图；斜向探测系统的接收站同样位于B点，通过与2号垂测站共用发射站，可以得到CB斜测链路的扫频电离图.试验系统具体的布站示意图如图4所示.各种探测数据时间上几乎是同步的.本文使用中国电波传播研究所研发的返回散射电离图智能判读算法(齐东玉等，2011；冯静等，2012，2014)和垂测电离图反演算法(蔚娜等，2016)，获得了返回散射电离图前沿和2个垂测站上空的电子浓度剖面.利用返回散射前沿数据和1号垂测站反演结果作为本文算法的输入，经过反演，得到探测方位上0～2000 km地面距离上空的二维电子浓度剖面.2号垂测站反演结果用于验证我们对应于该地面距离上空反演结果的准确性.基于反演的二维电子浓度剖面，利用射线追踪技术合成地面距离1000 km的斜测链路电离图，并与实测的斜测电离图进行对比，用以检验本文算法在斜测链路反射区域电子浓度的反演结果.

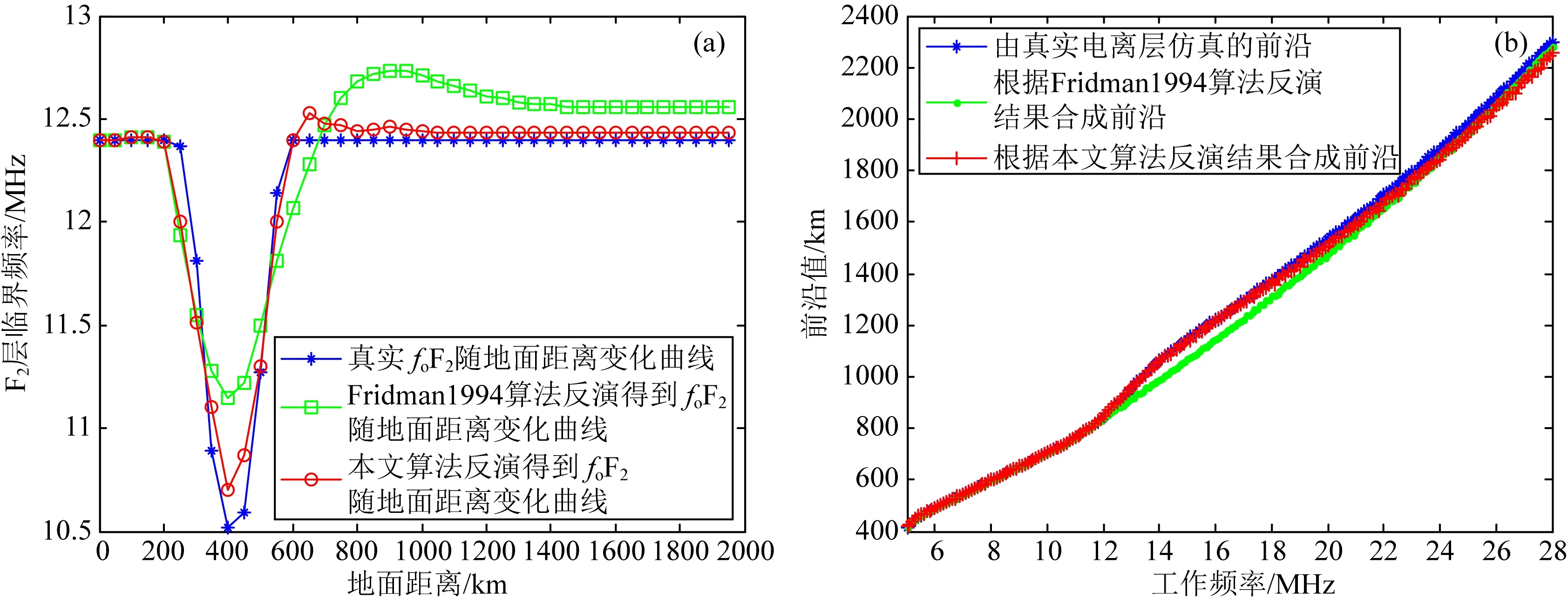
图3 本文算法和Fridman 1994算法对模拟数据反演结果的比较(a) 地面距离0～2000 km的foF2反演结果比较； (b) 根据反演结果合成返回散射前沿比较.Fig.3 Comparison between the inversion results of our algorithm and those of the algorithmpresented by Fridman and Fridman in 1994 using simulated data(a) Comparison of foF2 inversion results of ground distance 0～2000 km; (b) Comparison of the backscatter leading edges constructed using the inversion results.

下面给出两个具体的反演实例，分别为日落时段和白天的电离图.

如图5所示是一组日落期间准同步探测的电离图，其中返回散射电离图的前沿使用一条黑色实线来表示.日出日落期间，电离层发生倾斜，意味着电子浓度等值线不再是平面和球面，电子浓度存在较大起伏.图中，1号垂测站和2号垂测站的foF2分别为10.8 MHz和18.2 MHz，两站之间7.4 MHz的临界频率之差表明电离层在该方位上存在较大的梯度，具有不均匀电子浓度分布.这从返回散射前沿线的形态上也有所体现，从图5a可以看出前沿线为直线型，根据文献(焦培南，1990)，这对应于沿探测方向上在水平面有正电子浓度梯度的电离层.

图4 试验布站示意图Fig.4 Sketch map of experiment

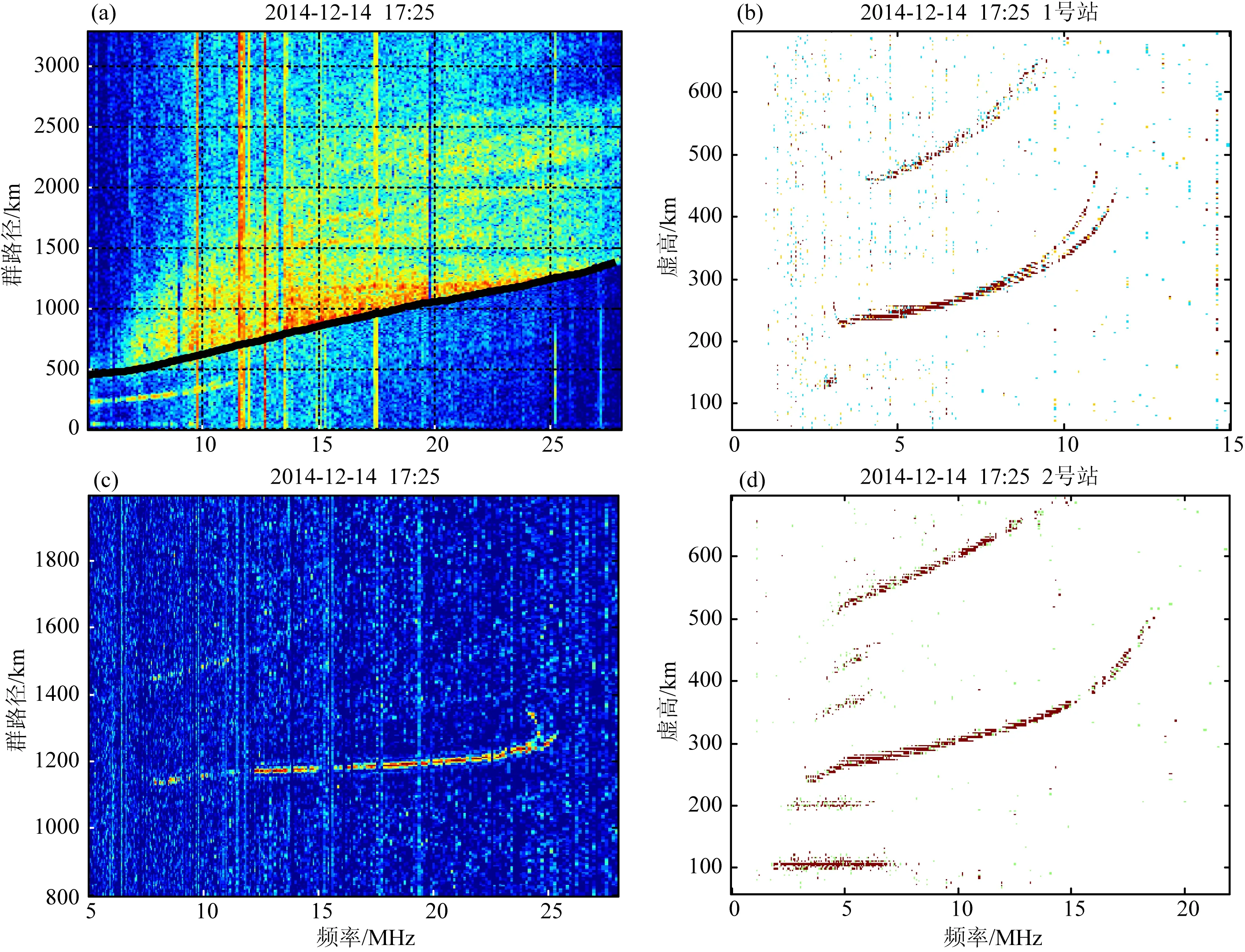
图5 2014年12月14日17∶25返回散射、垂测和斜测电离图(a) 返回散射电离图； (b) 1号垂测站电离图； (c) 斜测电离图； (d) 2号垂测站电离图.Fig.5 Ionograms for backscatter sounding (a), vertical sounding (b，d) and oblique sounding (c) at 15:25 on 14 December 2014

首先利用2号垂测站电子浓度剖面验证算法在地面距离1000 km上空的反演结果.如图6a所示，蓝色点划线是根据2号垂测站电离图反演的电子浓度剖面，临界频率为18.2 MHz，可将其视为真实剖面；红色点划线和绿色点划线分别是本文算法和Fridman1994算法在该垂测站上空的反演结果，临界频率分别为17.8 MHz和19.6 MHz.从图中可以看出，前者无论是临界频率还是整个剖面较后者都更接近于真实值.但同时我们也注意到，两种算法反演的F2层峰高均略低于实际峰高，差值为20 km.这是因为，算法使用的电离层模型(见2.2节)的峰高是固定值(等于1号垂测站的峰高)，而实际电离层的峰高随地面距离是变化的.这也是本文算法以后改进的一个方向.

图6b是在图5c实测斜测电离图上叠加了基于本文算法和Fridman 1994算法两种反演结果合成的斜测电离图.实测斜测电离图的F2层最高可用频率(MUF)为24.5 MHz，根据本文算法和Fridman 1994算法的反演结果合成斜测描迹的MUF分别为24.2 MHz和27.5 MHz.显然，本文算法合成的MUF非常接近实测值，与Fridman1994算法相比，精度提高了11%.由图中可以看出，算法合成的斜测F2层描迹与实测描迹吻合较好，只是群路径略低，同样是因为使用了固定峰高的电离层模型；但合成的E层斜测描迹与实际情况不太相符，这是由于两种算法都仅使用了F层前沿进行反演，而未使用E层前沿，因此反演得到的电离层结构中更多是反映F层的电子浓度分布，E层的信息较少.解决办法之一是利用返回散射E层和F层前沿进行联合反演，这需要研究合理的联合反演技术，以及开发有效的返回散射E层前沿提取技术，而从实测返回散射图上往往看不到E层回波的清晰前沿(如图5a所示，仅能看到F层前沿)，这或许可以考虑使用模型计算值来代替实测值，其可行性还需后续研究的检验.

图7给出了反演的探测路径上空的二维电子浓度剖面，可以看出，在0～300 km地面距离范围内，电离层基本是均匀的，之后随着地面距离的增加，电子浓度迅速增加，直至约800 km的地面距离处，电离层又呈现平稳状态.

图8给出了一组白天上午探测的电离图.在中纬地区，白天和夜间的电离层状态较日出和日落时段平稳，从图中也可以看出，1号垂测站和2号垂测站的临界频率之差仅为0.1 MHz，各层描迹的最小虚高也相差不大，表明返回散射探测路径上电子浓度存在很小的水平梯度，电离层近似为球面分层.观察图8a，返回散射前沿线呈现二次曲线型，而二次曲线型通常对应着球面分层或沿路径电子浓度有负水平梯度的电离层(焦培南，1990).

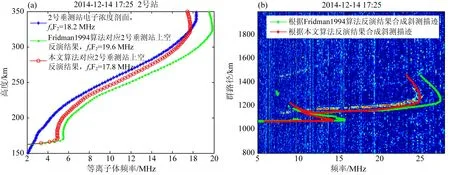
图6 本文算法与Fridman 1994算法对日落时段实测数据反演结果的比较(a) 反演2号垂测站电子浓度剖面比较； (b) 根据反演结果合成斜测电离图比较.Fig.6 Comparison between the inversion results of our algorithm and those of the algorithm presented by Fridman and Fridman in 1994 using measured data at sunset(a) Comparison of electron density profiles above the vertical sounding station of No.2;(b) Comparison of the constructed oblique sounding ionograms based on the inversion results.

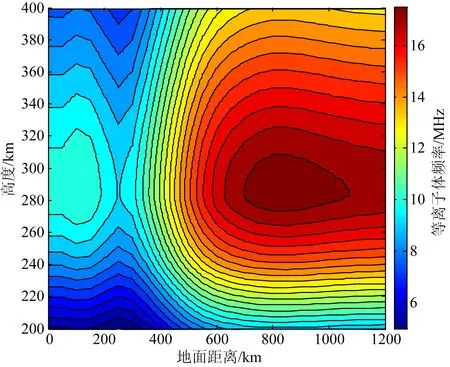
图7 二维电子浓度剖面(日落时段)Fig.7 Two-dimensional electron density profile (during sunset)

图9a和9b分别给出了本文算法和Fridman 1994算法对2号垂测站电子浓度剖面的反演结果以及合成斜测描迹的结果.从图9a可以看出，本文算法反演的剖面与真实剖面基本重合，F2层峰高低了约5 km；Fridman 1994算法反演的剖面比本文算法的反演误差大.两种算法反演的E层电子浓度剖面较F层误差稍大一些，这与前面讨论的原因一样——返回散射E层前沿没有参与反演.图9b中实测斜测电离图MUF、根据本文算法和Fridman 1994算法的反演结果合成斜测描迹的MUF分别为18.1 MHz、18.2 MHz和18.7 MHz，表明在水平电子浓度梯度较小的电离层条件下本文算法仍然优于Fridman 1994算法.需要说明的是，本文算法在反演电子浓度分布时，并不是在一开始就认定电子浓度分布是水平均匀的，而是仍然采用2.2节这种可以描述水平不均匀分布的二维电离层模型，通过本文提出的频段递增逐步逼近算法以及(7)式对模型空间做光滑性限制和约束，从而实现电子浓度反演.

图10给出了白天探测路径上空的二维电子浓度剖面，随着地面距离的增加，电子浓度变化不明显，电离层具有很小的水平电子浓度梯度.

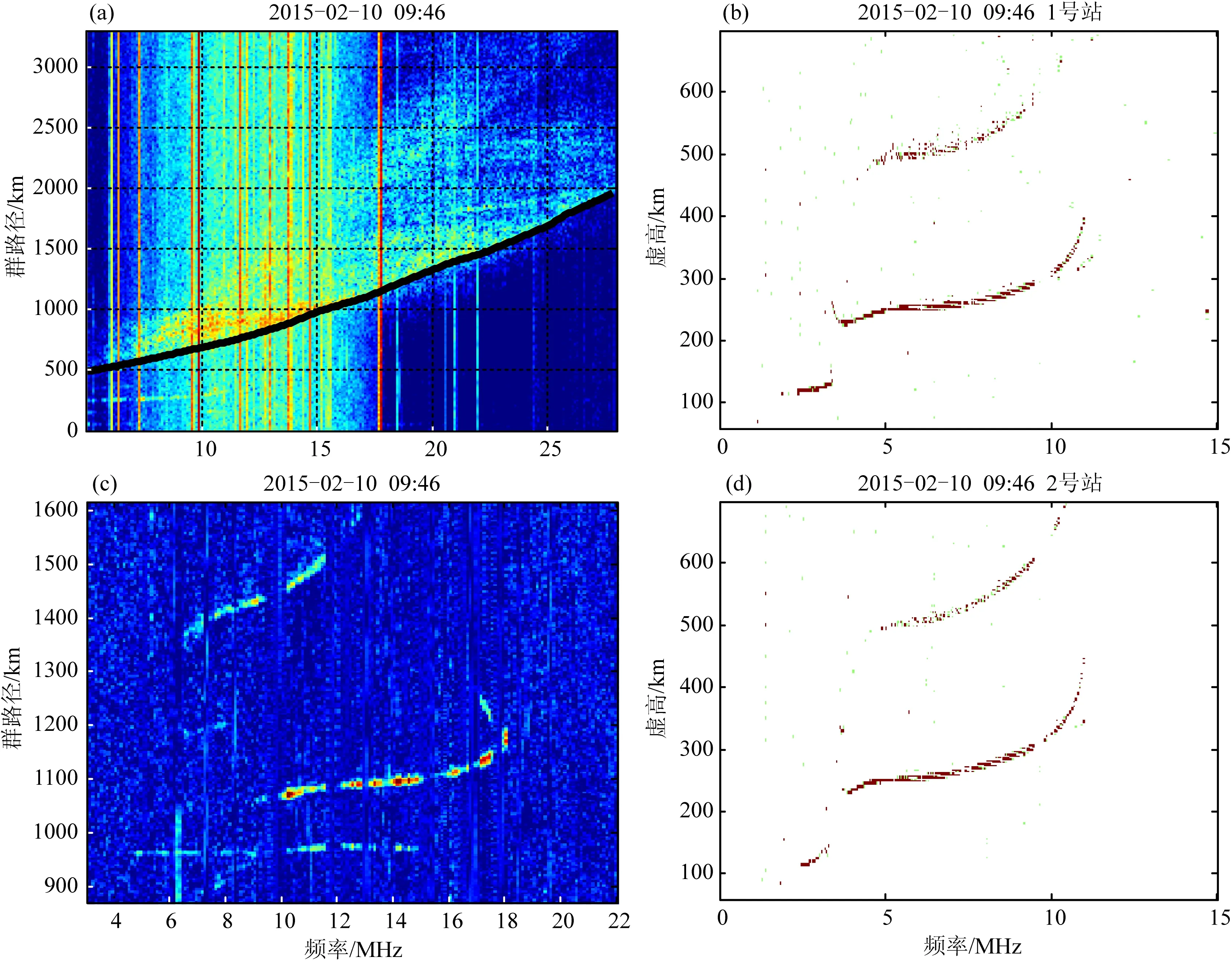
图8 2015年2月10日9∶46返回散射、垂测和斜测电离图(a) 返回散射电离图； (b) 1号垂测站电离图； (c) 斜测电离图； (d) 2号垂测站电离图.Fig.8 Ionograms for backscatter sounding (a), vertical sounding (b，d) and oblique sounding (c) at 9∶46 on 10 February 2015

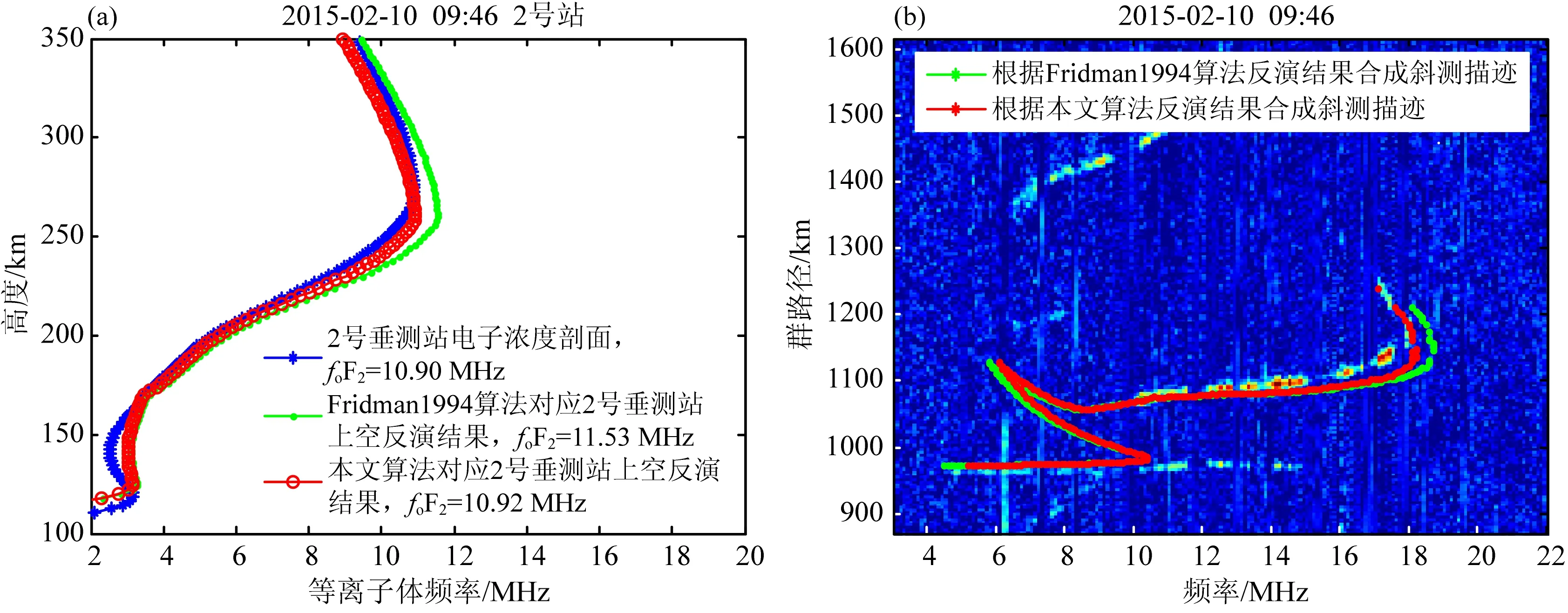
图9 本文算法与Fridman 1994算法对白天实测数据反演结果的比较(a) 反演2号垂测站电子浓度剖面比较； (b) 根据反演结果合成斜测电离图比较.Fig.9 Comparison between the inversion results of our algorithm and those of the algorithm presented by Fridman and Fridman in 1994 using measured data in the daytime(a) Comparison of electron density profiles above the vertical sounding station of No.2;(b) Comparison of the constructed oblique sounding ionograms based on the inversion results.

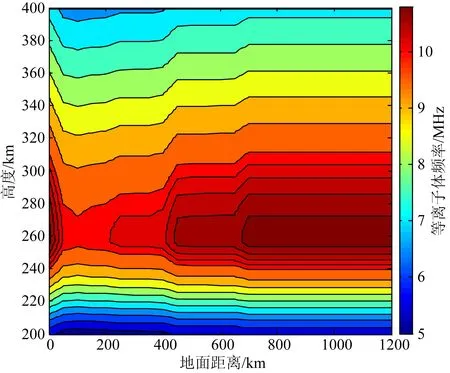
图10 二维电子浓度剖面(白天)Fig.10 Two-dimensional electron density profile (in the daytime)

图11 本文算法与Fridman 1994算法的反演结果统计Fig.11 Statistics of the inversion results

本次反演试验选取了2014年6月至2015年6月期间的50组数据进行了反演，数据涵盖了春、夏、秋、冬四个季节和日出、日落、白天、夜间四个时段，能够充分体现电离层状态的多样性.将本文算法和Fridman 1994算法反演得到的2号垂测站临界频率与其对应的实测结果进行差值比较，得到两种反演算法的误差统计结果，如图11所示.本文指定临界频率误差的允许范围为0.0～1.0 MHz.如果临界频率的误差超过1.0 MHz，说明反演结果不正确；临界频率的误差在0.0～0.5 MHz之间，则说明反演结果相当精确.从图11可知，本文算法有86%的反演结果控制在误差范围内，高于Fridman 1994算法(80%)，并且前者有70%的反演结果相当精确，后者则为55%.可见本文算法明显优于Fridman 1994算法.本次针对实测数据的反演试验也充分说明，我们建立的算法无论反演白天和夜间这种电离层较平稳时期的电离层状态，还是重构日出/日落时段等电子浓度分布具有较大梯度的电离层水平不均匀结构，均有很好的效果，表明了该算法在处理复杂多变的实际探测的返回散射数据中的应用价值.

4 讨论

本文采用电离层垂直剖面形状不变的简化模型作为反演使用的电离层模型，这个模型假设电离层电子浓度分布的垂直剖面的形状沿水平方向近似不变，且最大电子浓度高度沿水平方向不变，只是最大电子浓度值在水平方向按(1)式变化.它可以描述较为陡峭的水平电子浓度变化，例如中纬电离槽、中纬日出日落电离层等.采用该电离层模型实际是对解空间作了一定的约束，减少了解的非唯一性，有利于反演结果的稳定.文章中展示的实测返回散射电离图的反演结果与真实结果吻合得很好，表明该模型对实际复杂电离层模型的简化近似是合理的，在实际应用中可行.

对确定电离层中尺度和大尺度不均匀结构的空间分布来说，返回散射前沿反演技术是非常有效的一种方法，能够提供全面的、反映远至数千千米的电离层电子浓度水平分布情况，而这对高频无线电波传播来说是至关重要的.需要说明的是，并不是所有的电离层结构都被反演出来，在电波反射点以上的区域，反演结果与实际情况有较大的差别，这可以从图1来解释.从图1可以看到，形成最小时延的射线没有经过上述区域，因此没有足够的信息来确定它们的电子浓度分布.尽管如此，我们反演信息的有效高度范围对以电离层为传播媒介的短波应用系统(比如天波超视距雷达、短波通信、短波技侦等)已经足够了.另外，高度在100 km到大约200 km的区域的电子浓度很小，对最小时延的影响很小，反演结果中它们也有较大误差，这是因为我们目前算法使用的返回散射前沿是F层前沿.为了提高F2层以下的电子浓度反演精度，需要考虑利用返回散射E层和F层前沿进行联合反演，这将是后续研究工作的一个重要内容.

5 结论

本文建立了一种利用高频返回散射前沿反演电离层电子浓度的方法.基于解空间约束的思想，提出了频段递增逐步逼近反演算法，采用垂直剖面形状不变的电离层模型，同时结合运用求解非线性问题的Newton-Kontorovich方法和求解线性不适定问题的Tikhonov正则化方法，很好地对解空间做出限制，保证解的可靠性和唯一性，具有较高的反演精度，能够有效诊断电离层的水平不均匀性.算法的输入为： ① 实测的返回散射前沿； ② 返回散射发射站上空的电子浓度剖面； ③ 频率范围划分为n个频段对应的实测前沿的n个测量误差先验值δ1，δ2，…，δn.算法的输出是返回散射探测方位上的能够反映电离层水平不均匀结构的二维电子浓度分布.实际上，算法的输入②可以换成返回散射探测路径上任意位置垂测站反演的垂直电子浓度剖面.

本文分别使用模拟数据和实测数据对所建算法的可靠性和准确性进行了验证.Fridman和Fridman 1994年提出的利用返回散射前沿反演电离层算法能够有效建立探测方位上的二维电子浓度分布，为了考查本文算法的精度，我们与Fridman 1994算法的反演结果进行了对比.结果表明，无论是存在严重电离层扰动的模拟数据，还是水平方向上具有较大梯度的实测数据，亦或是水平方向近似均匀的数据，本文算法的反演精度都要高于Fridman 1994算法，说明我们的反演理论是正确的，是对Fridman 1994算法的有效改进.多次反演试验证明，本文建立的反演算法能够较好地反映探测方位上电离层水平不均匀特性，而且对返回散射前沿的判读误差不敏感，具有一定的抗数据误差能力，在处理复杂多变的实测返回散射电离图中有很好的应用价值.

Benito E, Bourdillon A, Saillant S, et al. 2008a. Inversion of HF backscatter ionograms using elevation scans.JournalofAtmosphericandSolar-TerrestrialPhysics, 70(15): 1935-1948. Benito E, Saillant S, Molini J P, et al. 2008b. Inversion of backscatter ionograms optimization by using simulated annealing and genetic algorithms.∥ 2008 IEEE International Geoscience and Remote Sensing Symposium. Boston, MA: IEEE, III-1127-III-1130.

Caratori J, Goutelard C. 1997. Derivation of horizontal ionospheric gradients from variable azimuth and elevation backscatter ionograms.RadioScience, 32(1): 181-190.

Chuang S L, Yeh K C. 1977. A method for inverting oblique sounding data in the ionosphere.RadioScience, 12(1): 135-140. Coleman C J. 1998. A ray tracing formulation and its application to some problems in over-the-horizon radar.RadioScience, 33(4): 1187-1197.

Croft T A. 1972. Sky-wave backscatter: A means for observing our environment at great distances.ReviewsofGeophysics, 10(1): 73-155.

DuBroff R E, Rao N N, Yeh K C. 1979. Backscatter inversion in spherically asymmetric ionosphere.RadioScience, 14(5): 837-841.

Dyson P L. 1991. A simple method of backscatter ionogram analysis.JournalofAtmosphericandTerrestrialPhysics, 53(1-2): 75-88.

Feng J, Li X, Qi D Y. 2012. Methods for extracting backscatter ionogram leading edges.ChineseJournalofSpaceScience(in Chinese), 32(4): 524-531.

Feng J, Qi D Y, Li X, et al. 2014. Methods for auto-identification of propagation modes from backscatter ionograms.ChineseJournalofRadioScience(in Chinese), 29(1): 188-194.

Fridman O V, Fridman S V. 1994. A method of determining horizontal structure of the ionosphere from backscatter ionograms.JournalofAtmosphericandTerrestrialPhysics, 56(1): 115-131.

Fridman O V, Nosov V E, Boitman O N. 1994. Reconstruction of horizontally-inhomogeneous ionospheric structure from oblique-incidence backscatter experiments.JournalofAtmosphericandTerrestrialPhysics, 56(3): 369-376.

Fridman S V. 1998. Reconstruction of a three-dimensional ionosphere from backscatter and vertical ionograms measured by over-the-horizon radar.RadioScience, 33(4): 1159-1171. Fridman S V, Berkey F T. 1998. Utilization of sky-wave backscatter sounders for real-time monitoring of ionospheric structure over extended geographic regions.GeophysicalResearchLetters, 25(6): 885-888. Fridman S V, Nickisch L J. 2001. Generalization of ionospheric tomography on diverse data sources: Reconstruction of the three-dimensional ionosphere from simultaneous vertical ionograms, backscatter ionograms, and total electron content data.RadioScience, 36(5): 1129-1139, doi: 10.1029/1999RS002405. Fridman S V, Nickisch L J, Hausman M. 2009. Personal-computer-based system for real-time reconstruction of the three-dimensional ionosphere using data from diverse sources.RadioScience, 44: RS3008, doi: 10.1029/2008RS004040. Fridman S V, Nickisch L J, Hausman M. 2012. Inversion of backscatter ionograms and TEC data for over-the-horizon radar.RadioScience, 47: RS0L10, doi: 10.1029/2011RS004932.

Jacquet F, Caratoff J, Dorizzi B. 2001. Derivation of the ionospheric structure over extended geographical regions from azimuth and elevation scan backscatter ionograms: A modular neural network approach.RadioScience, 36(5): 1043-1052. Jiao P N. 1990. The effect of the horizontal density gradient onPmin(f) curve.ChineseJournalofRadioScience(in Chinese), 5(1): 18-22.

Landeau T, Gauthier F, Ruelle N. 1997. Further improvements to the inversion of elevation-scan backscatter sounding data.JournalofAtmosphericandSolar-TerrestrialPhysics, 59(1): 125-138.

Liu W, Jiao P N, Wang J J, et al. 2005. A study of the disturbance in the ionosphere using ray tracing technology.ChineseJ.Geophys. (in Chinese), 48(3): 465-470.

Liu W, Jiao P N, Wang S K, et al. 2008. Short wave ray tracing in the ionosphere and its application.ChineseJournalofRadioScience(in Chinese), 23(1): 41-48.

Norman R J. 2003. Backscatter ionogram inversion.∥ Proceedings of the International Radar Conference.Adelaide,SA,Australia:IEEE, 368-374. Norman R J, Dyson P L. 2006. HF radar backscatter inversion technique.RadioScience, 41: RS4010, doi: 10.1029/2005RS003355. Qi D Y, Feng J, Li X. 2011 Algorithms for automatic cleaning of backscatter ionograms.ProgressinGeophys. (in Chinese), 26

(6): 1925-1930, doi: 10.3969/j.issn.1004-2903.2011.06.005. Rao N N. 1974. Inversion of sweep-frequency sky-wave backscatter leading edge for quasiparabolic ionospheric layer parameters.RadioScience, 9(10): 845-847.

Rao N N. 1975. Analysis of discrete oblique ionogram traces in sweep-frequency sky-wave high resolution backscatter.RadioScience, 10(2): 149-153.

Song J, Zhao Z Y, Zhou C, et al. 2011. Inversion of HF sweep-frequency backscatter ionograms.ChineseJ.Geophys. (in Chinese), 54(8): 1953-1959, doi: 10.3969/j.issn.0001-5733.2011.08.002. Tikhonov A N, Arsenin V Y. 1977. Solutions of Ill-posed Problems. New York: Halsted Press. Wei N, Liu W, Lu Z X, et al. 2016. The electron density profile inversion for incompletely developed case of F1layer.ChineseJ.Geophys. (in Chinese), 59(3): 778-790, doi: 10.6038/cjg20160302.

Xie S G. 2001. A study on the ionospheric parameters of backscatter ionograms [Ph. D. thesis] (in Chinese). Wuhan: Wuhan University.

Xiong N L, Tang C C, Li X J. 1999. Introduction to Ionospheric Physics (in Chinese). Wuhan: Wuhan University Press.

Zhu P, Zhou C, Zhang Y N, et al. 2015. F region electron density profile inversion from backscatter ionogram based on international reference ionosphere.JournalofAtmosphericandSolar-TerrestrialPhysics, 129: 111-118.

附中文参考文献

冯静, 李雪, 齐东玉. 2012. 返回散射电离图的前沿提取方法. 空间科学学报, 32(4): 524-531.

冯静, 齐东玉, 李雪等. 2014. 返回散射电离图传播模式的自动识别方法. 电波科学学报, 29(1): 188-194.

焦培南. 1990. 水平电子浓度梯度对Pmin(f)线的影响. 电波科学学报, 5(1): 18-22.

柳文, 焦培南, 王俊江等. 2005. 利用射线追踪研究电离层扰动. 地球物理学报, 48(3): 465-470.

柳文, 焦培南, 王世凯等. 2008. 电离层短波三维射线追踪及其应用研究. 电波科学学报, 23(1): 41-48.

齐东玉, 冯静, 李雪. 2011. 返回散射电离图噪声和干扰的自动消除方法. 地球物理学进展, 26(6): 1925-1930, doi: 10.3969/j.issn.1004-2903.2011.06.005.

宋君, 赵正予, 周晨等. 2011. 高频返回散射扫频电离图的反演. 地球物理学报, 54(8): 1953-1959, doi: 10.3969/j.issn.0001-5733.2011.08.002.

蔚娜, 柳文, 鲁转侠等. 2016. F1层未充分发展时的电离层剖面反演. 地球物理学报, 59(3): 778-790, doi: 10.6038/cjg20160302. 谢树果. 2001. 斜向返回探测电离层参数反演方法研究[博士论文]. 武汉: 武汉大学.

熊年禄, 唐存琛, 李行健. 1999. 电离层物理概论. 武汉: 武汉大学出版社.

(本文编辑 胡素芳)

Reconstruction of horizontally-inhomogeneous ionospheric structure using HF sky-wave backscatter ionograms

FENG Jing1,2, NI Bin-Bin1, ZHAO Zheng-Yu1, LIU Wen2, WEI Na2, LOU Peng2

1SchoolofElectronicInformation,WuhanUniversity,Wuhan430079,China2ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China

High-frequency (HF) sky-wave backscatter sounding, as a powerful tool for detecting the ionosphere and studying the characteristics of radio channels, can be used to monitor the ionosphere continuously at a remote distance and to acquire the ionospheric parameters in a large area. Backscatter ionograms can be obtained showing the relationship between operating frequency, group path and echo amplitude. Since an ionogram carries the information of the ionospheric profile along the detection path, the ionospheric parameters can be evaluated through the inversion technique. An algorithm for backscatter sounding ionogram inversion is developed based on the restriction of solution space to reconstruct the horizontally inhomogeneous structures of the ionosphere. Furthermore, the Newton-Kontorovich method that generally treats nonlinear operator equations and the Tikhonov regularization method that generally deals with ill-posed problems are effectively combined to resolve the equations. The algorithm can get a stable and unique solution under the solution space limitation. In terms of comparisons between model results and observation data, the developed algorithm proves reliable convergence, insensitivity to measurement errors, and higher accuracy for the inversion of ionospheric structures than the method of Fridman and Fridman (1994). Our algorithm not only can inverse horizontal changes in electron density under quiet conditions (at night or during the daytime at mid-latitudes), but also can diagnose the horizontally inhomogeneous structures of the ionosphere during sunrise or sunset periods with high accuracy. This consequently demonstrates the application value of the proposed algorithm in the treatment of the complex and volatile measured backscatter ionograms.

Backscatter; Ionogram; Ionosphere; Inversion; Reconstruction; Inhomogeneous

10.6038/cjg20160901.

国防技术基础科研项目(JSHS2014210A002)，中国电科技术创新基金项目(JJ-QN-2013-28)，国家自然科学基金项目(61331012)资助.

冯静，女，1981年生，山东人，高级工程师，博士研究生，主要从事电离层物理及电波传播等相关研究工作.E-mail: hellen1917@163.com

10.6038/cjg20160901

P352

2016-03-08，2016-05-11收修定稿

冯静, 倪彬彬，赵正予等. 2016. 利用高频天波返回散射反演电离层水平不均匀结构. 地球物理学报，59(9):3135-3147,

Feng J, Ni B B, Zhao Z Y, et al. 2016. Reconstruction of horizontally-inhomogeneous ionospheric structure using HF sky-wave backscatter ionograms.ChineseJ.Geophys. (in Chinese),59(9):3135-3147,doi:10.6038/cjg20160901.