单轴和多轴疲劳准则下的车轮疲劳强度分析

王悦东，盛杰琼

(大连交通大学 交通运输工程学院，辽宁 大连 116028)



单轴和多轴疲劳准则下的车轮疲劳强度分析

王悦东，盛杰琼

(大连交通大学 交通运输工程学院，辽宁 大连 116028)

为了分析城际动车组车轮的疲劳强度，首先建立城际动车组车轮的有限元模型，依据国际铁路联盟的UIC510-5 标准以及欧洲的EN 标准模拟车轮在直线、曲线和道岔工况下的应力；并依据车轮的单轴疲劳准则 Haigh 形式的Goodman曲线图分析评估城际动车组车轮的疲劳强度，以及利用多轴疲劳准则Crossland曲线来评估辐板孔的疲劳强度.结果表明，城际动车组车轮能满足静强度和疲劳强度性能要求.疲劳强度的薄弱部位是垂直或者平行于车轮半径的辐板孔的孔边缘中间位置或中间位置连线上的点，以及辐板与轮毂过渡部位.

车轮；辐板孔；有限元； 疲劳强度；疲劳准则

0 引言

车轮是保证列车运行安全的重要部件之一，其工况比较复杂，由于机车车辆通过曲线、道岔导致车轮承载工况恶劣，其疲劳强度方面的问题日益凸显，车轮失效的主要形式是疲劳断裂.其中车轮辐板孔裂纹问题对车轮的疲劳强度有很大的影响，因此依据国际标准对车轮进行强度分析与评估具有重要的意义[1].

目前，我国尚未制定城市轨道车辆车轮的国家标准，主要采用国际铁路联盟组织的UIC510-5[2]和欧洲联盟标准BS EN13979-1[3]，两种标准基本相同，规定了车轮静强度和疲劳强度要求及校核方法，美国AAR标准S 660-83《机车和货车车轮设计分析评定办法》[4]通过比较不同车轮设计的应力分析结果和基础数据，来对车轮进行评定.这一规范仅给出了车轮静强度分析及评定标准.李树林、石启龙等[5]利用UIC510-5标准对CRH3型车轮进行疲劳强度分析，计算3种工况下车轮各评估点的平均应力值和应力幅值，应用Goodman曲线进行疲劳强度分析，利用有限元名义应力法和ANSYS/WORKBENCH得出车轮疲劳寿命预测图和安全系数图对车轮进行疲劳寿命分析.张澎湃、刘金朝等[6]提出了修正的Crossland疲劳准则，确定准则中应力张量第1应力不变量最大值的系数，以轴对称车轮和非轴对称车轮为研究对象，对主应力法和修正的Crossland疲劳准则评定方法进行了比较分析.刘旭[7]采用基于UIC510-5标准中的单轴疲劳理论的车轮疲劳强度评定准则和Dang-Van多轴高周疲劳评定准则这2 种疲劳评价方法对同一车轮进行疲劳强度计算，并选取关键点进行应力分析，比较2 种方法的安全度和适用范围以及评估车轮的疲劳薄弱部位.本文以城际动车组车轮为研究对象，运用Hypermesh软件对车轮进行建模，基于ANSYS软件对车轮进行有限元分析，根据UIC510-5标准中单轴疲劳准则以及Crossland曲线多轴疲劳准则对车轮强度进行疲劳强度分析评价.

1 单轴及多轴疲劳准则

1.1 单轴疲劳准则

有关文献指出，结构产生疲劳裂纹方向与最大主应力方向相互垂直，因此可以假设车轮的疲劳破坏是由最大主应力方向的应力造成的.参照UIC510-5 和BS EN 13979-1-2003标准，将三向应力状态转换为单向应力状态.

首先确定车轮在不同载荷工况作用下的主应力值和方向，将所有载荷工况作用下的最大主应力方向确定为基本应力分布方向，其值为计算最大主应力，计算其与结构基准(节点位置与车轮轴线组成的平面)的夹角，如图1(a)所示；将在其它载荷工况作用下的主应力投影到最大主应力方向上，其投影值最小的应力值确定为最小主应力，如图1(b)所示.由该位置的最大和最小主应力值计算平均应力和应力幅，如下式所示.然后用Haigh形式的Goodman疲劳曲线评定车轮的疲劳强度.

(1)

(2)

(3)

图1 主应力方向确定及其投影示意图

1.2 Crossland多轴疲劳准则

由于带辐板孔的车轮在运行过程中各点受力复杂，因此采用复杂应力状态下的多轴疲劳准则对车轮危险区域进行判定.非轴对称车轮采用Crossland疲劳准则对车轮辐板孔的表面节点进行评定，在多向应力状态下，基于动态八面体剪应力，Crossland准则用最大应力和安全指数对车轮辐板孔的疲劳强度进行分析[8].

Crossland疲劳准则属于多轴疲劳强度评定方法，该疲劳准则在应力幅值偏张量第2不变量的基础上考虑了静水应力最大值的影响， Crossland准则用最大应力和安全指数对车轮辐板孔的疲劳强度进行分析.其最大应力为：

(4)

式中,σIa、σIIa、σIIIa为所有涉及到载荷循环的主应力幅.

将这个参数与一个极限值比较，该极限量取决于材料特性和一个最大不变线性量II,max.

(5)

式中,σI,max、σII,max、σIII,max为所有涉及到载荷循环的主应力最大值.

克罗斯兰德(Crossland)准则公式为：

(6)

常量B和β取决于材料特性σA和σP,σA为材料的弯曲疲劳极限；σP为材料的扭转疲劳极限.安全系数S1和S2的关系式分别为：

2 有限元建模

2.1 车轮机械参数

城际动车组车轮采用整体轧制车轮，车轮踏面是车轮材质为ER8，其弹性模量E=200 000N/mm2，泊松比μ=0.3，摩擦系数为0.15.车轮新轮直径860mm，旧轮直径780mm，主动车轮辐板上有8个φ34mm的销孔，轴重为18t.屈服极限为355MPa，疲劳极限为180MPa，弯曲疲劳极限为245MPa，扭转疲劳极限为177.5MPa.

2.2 车轮模型

因为车轮在工作寿命期间会出现踏面磨耗、表面擦伤等疲劳破坏，当到一定程度时需要旋轮处理，直到车轮踏面达到磨耗到限状态，所以磨耗轮的应力水平高于新造车轮，这里选择磨耗轮进行计算，来保证车轮在整个使用周期的安全.首先使用Hypermesh软件对车轮进行有限元建模，如图2所示.车轮和车轴选用SOLID185三维六面体单元及少部分四面体单元进行模拟.通过先对截面划分网格，然后扫掠生成体单元的方式生成有限元模型，磨耗轮结构有限元模型由273 404个节点，244 609个单元组成，其中主要是8节点六面体实体单元，还有部分四面体单元.为了模拟轮轴过盈配合，取车轴的一部分进行分析，车轴部分由51 168个节点，48 526个单元组成.

选用三维面到面接触单元CONTA174及目标单元TARGE170进行轮轴过盈配合部位的接触模拟，轮轴过盈配合区域的接触对由10 260个4节点接触单元和10 818个4节点目标单元组成，通过接触单元实常数设置过盈量为0.1mm.在车轴的两个端面施加限制x，y，z移动的约束.

图2 车轮有限元模型

2.3 车轮载荷工况

根据UIC510-5标准，工况按直线工况、曲线工况和道岔工况3种工况来进行疲劳强度校核，各工况所受载荷如下：

工况1：直线(轮对对中)：

Fz1=1.25P=110 363N，Fy1=0

工况2：曲线(轮缘靠钢轨)：

Fz2=1.25P=110 363N，

Fy2=0.7P=61 803N

工况3：道岔(轮缘内侧面接触钢轨)：

Fz3=1.25P=110 363N，

Fy3=0.6Fy2=0.42P=37082N

其中,P为每个轮对作用在轨道上的垂向力的一半，各力在同一断面的作用位置如图3.

考虑到车轮在旋转过程中，踏面其他位置与轨面接触时仍会对危险截面产生影响，因此应该综合考虑全部载荷工况对危险截面上点的影响，对车轮所有截面进行加载计算，考虑辐板孔对疲劳强度的影响，并为了减小计算规模选取三个载荷作用截面位置施加图3所示的三个机械载荷工况，分别为经过轮心及辐板孔轴线的平面、经过轮心与辐板孔相切的平面、经过轮心及两辐板孔中心连线中点的平面，如图4中截面1、2、3.3种截面位置与直线、曲线、道岔疲劳载荷工况组合构成9种工况，如表1所示.

图3 载荷作用位置

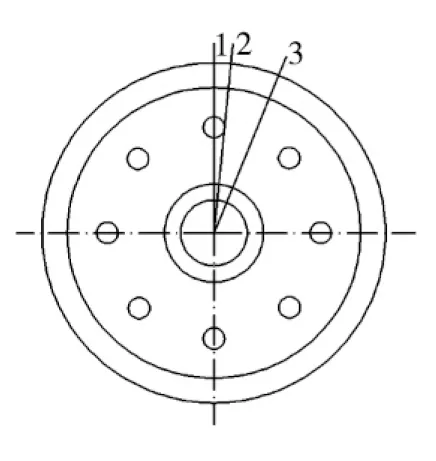
图4 车轮的加载截面位置

表1 不同载荷作用截面的计算载荷工况

3 车轮静强度分析

根据标准UIC510-5及EN13262，在所有静强度计算工况中，计算所得应力不应超过ER8钢的屈服极限355MPa.通过把有限元模型导入有限元分析软件ANSYS中进行计算，得到车轮在9种工况下的最大Von Mises应力分别为252.68、270.46、249.32、250.60、282.22、249.31、250.95、270.62、249.41 MPa，可以看出同一截面位置下，曲线工况应力最大，直线和道岔工况应力较小且相似，其中截面2位置的曲线工况应力最大，但都小于屈服极限355 MPa，说明9种工况下的车轮都满足静强度要求.由于三个截面位置的云图相似，以截面1位置的Von Mises云图为例如图5所示，可以看出轮毂孔边缘位置应力最大，说明过盈配合对车轮的应力影响较大.

图5 截面1位置的直线、曲线、道岔工况

4 车轮疲劳强度分析

评估车轮的疲劳强度时首先应选取合适的评估点，由于车轮在列车运行时会受到两种形式的交变应力，一种是车轮旋转产生的高频应力，另一种是来自轨道工况，如直线、曲线、道岔工况之间转换带来的低频交变应力.因此，当选取车轮的疲劳评估点时应该综合考虑所有工况，并找出所有工况下最易发生疲劳破坏的截面，然后在选取的评估面上选取评估点，由于辐板和辐板孔附近是疲劳破坏的高发部位，所以在三个载荷作用截面及其通过的辐板孔的位置选取评估点.

4.1 辐板疲劳强度分析

通过ANSYS有限元计算并输出计算模型节点的应力分布信息，编制小程序提取评估点的主应力，并用单轴疲劳准则算出最小主应力、平均应力和应力幅值，生成Haigh形式的Goodman曲线来评定车轮的疲劳强度，如图6所示.

图6 辐板疲劳评估结点应力幅与许用应力比较Haigh图

通过以上Haigh形式Goodman曲线图可以看出在9种工况下，车轮辐板及辐板孔边的应力均值σm和应力幅值σa均落在Haigh形式的Goodman疲劳极限图的范围内，评估点的应力幅值均小于疲劳极限180 MPa，其中三个位置的直线工况的应力幅值均小于100 MPa，且9种工况的最小安全系数都大于1，说明单纯机械载荷下新轮辐板和辐板孔边的疲劳强度在这9种工况下均满足要求由评估点的计算结果可以看出这9种工况的安全系数最小的位置基本位于内侧辐板孔边垂直于力作用线的直径端点上，即图7中点8位置上的点上，和车轮外侧辐板与轮毂过渡部位的点上，说明这些部位是磨耗轮疲劳强度的薄弱部位.

图7 关键点位置

4.2 车轮辐板孔疲劳强度分析

运用Crossland多轴疲劳评价准则对新轮辐板孔表面结点进行9种工况下的疲劳强度评估，计算评估点的最大剪应力和第一最大不变量，并按照截面1、2、3分组绘制Crossland曲线，如图8所示.结果中正方形点为直线工况下评估点，菱形点为曲线工况下评估点，三角形点为道岔工况下评估点.

(a) 截面1位置直线、曲线、道岔工况

(c) 截面3位置直线、曲线、道岔工况

由以上计算结果可以得出在三个截面位置的直线、曲线、道岔工况下，评估点的结果均在极限要求范围内，所以辐板孔上的评估点在这9种工况下都满足疲劳强度要求.

为了更详细分析各工况下磨耗轮辐板和辐板孔边缘的应力状态和疲劳强度，选取截面1位置三个工况为例进行分析.通过计算得到了的所有评估点的最大主应力、最小主应力、应力均值、应力幅值和安全系数，选出其中危险部位的16个关键点，如图7所示.其中评估点1～4点为辐板外侧辐板孔边缘的点，5～8点为辐板内侧辐板孔边缘的点.9～12点为辐板外侧与力作用线平行线上的点，13～16点为辐板内侧与力作用线平行线上的点.

经过计算可以得出磨耗轮截面1位置三种工况下，辐板孔边缘直径方向的评估点1、3、5、7应力均值为负值，说明辐板孔边缘直径方向基本处于压应力状态，直线、曲线、道岔工况的最大压应力分别为-82.22、-122.81、-138.84 MPa；辐板孔边缘垂直直径方向的评估点2、4、6、8应力均值为正，说明辐板孔边缘垂直直径方向处于拉应力状态，直线、曲线、道岔工况的最大拉应力分别为100.67、198.85、176.93 MPa.这就可以解释了辐板孔裂纹容易出现在垂直车轮直径的辐板孔直径端点处，及拉应力是导致裂纹在此处萌生的原因，也可以看出曲线和道岔工况下的应力较大.辐板外侧的点9～12应力均值主要为负值，说明辐板外侧主要受压应力，辐板内侧的点13～16中辐板与轮毂和轮辋过渡部位应力均值为正，说明这两处主要为拉应力，而靠近辐板孔车轮直径方向的点，应力均值为负，说明此区域主要为压应力.从16个评估点的安全系数可以看出，车轮孔边评估点相比辐板上的评估点的安全系数要小，说明辐板孔周围相比辐板更容易发生疲劳破坏.

5 结论

根据本文的计算结果得出以下结论：

(1) 由静强度及应力分析结果可以看出，9种工况的磨耗轮满足静强度要求.过盈配合对车轮应力影响较大，截面位置对应力的影响不大，且曲线工况应力最大，其中磨耗轮的截面2位置曲线工况应力值最大;

(2) 由疲劳强度分析结果可以看出在 9种工况下，运用Haigh形式的Goodman曲线评估车轮疲劳强度表明辐板上的点均满足疲劳强度要求，其中曲线工况应力幅值最大.通过Crossland疲劳准则分析得出各工况下的车轮的辐板孔满足疲劳强度要求，且曲线工况下安全系数最小，所以曲线工况是车轮最危险的工况.应力分析结果表明垂直或者平行于车轮半径的辐板孔的孔边缘中间位置或中间位置连线上的点和辐板与轮毂过渡的部位是车轮疲劳的薄弱部位.

[1]田剑锋．基于标准的某地铁车辆车轮强度校核[D]．成都：西南交通大学,2013.

[2]International Union of Railways. UIC510-5 Technical Approval of Solid WheeIs[S].[s.l.]:[s.n.],2003.

[3]BS EN 13979-1,Railway Application-Wheelsets and Bogies-Monobloc Wheels-Technical Approval Procedure-Part1: Forged and Rolled Wheels[S]. [s.l.]:[s.n.], 2003.

[4]Association of American Railroads Procedure for the Analytic Evaluation of Locomotive and Freight Car Wheel Designs[M]. Manual of Standards and Recommended Practices Section G—Wheels and Axles,1998:G31-G34.

[5]李树林,石启龙,杨建伟,等.CRH3型动车组车轮的疲劳寿命分析[J]．机械设计与制造,2011(12):28-230.

[6]张澎湃,刘金朝,张斌,等.基于主应力法和修正的Crossland疲劳准则的动车组车轮疲劳强度评定办法,中国铁道科学,2014, 35(2):35-39.

[7]刘旭,张开林,姚远,等.两种评定准则下的车轮疲劳强度分析 [J]．机车电传动,2012(4)23-25.

[8]尚德广,王德俊.多轴疲劳强度[M].北京：科学出版社,2007.

Analysis of Wheel Fatigue Strength Under Uni-Axial and Multi-Axis Fatigue Criterions

WANG Yuedong, SHENG Jieqiong

(School of Traffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116028, China)

In order to analyze intercity EMU wheel fatigue strength, finite element model of intercity EMU wheel is establish according to the International Union of Railways UIC510-5 standards and the European EN standard, and the stress of wheel in straight line, curve and turnout and other conditions is simulated. Based on Haigh Goodman curve diagram，which is uniaxial fatigue criterion of wheel, fatigue strength of intercity EMU wheel is analyzed, and the fatigue strength of the plate hole is analyzed by using multiaxial fatigue criterion crossland curve. The results show that intercity EMU wheels can meet performance requirements of static strength and fatigue strength. The position of the weakest fatigue part of the wheel is on a point of the hole edge vertical or parallel to the wheel radius and in the middle or the middle position of the hole, the transition part of wheel hub and wheel plate.

wheel; plate hole; finite element; fatigue strength; fatigue criterions

1673- 9590(2016)02- 0047- 06

2015- 05- 08

国家自然科学基金项目资助(51208702)；辽宁省高等学校优秀人才支持计划 (LJQ2013052)

王悦东(1977-)，男，副教授，博士，主要从事车辆结构分析与现代设计方法的研究E- mail:wydstar@163.com.

A