非奇异H -矩阵的一类迭代判别法
张俊丽
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
非奇异H -矩阵的一类迭代判别法
张俊丽
(内蒙古民族大学 数学学院,内蒙古 通辽 028043)
非奇异H-矩阵应用广泛,但在实用中其判定十分困难。根 -对角占优矩阵与非奇异H-矩阵的关系,给出一类非奇异H-矩阵的迭代判定准则,对已有的相关结果进行推广和改进,并用数值算例验证了该判定准则的有效性。
非奇异H-矩阵;-对角占优矩阵;不可约;非零元素
1 预备知识
非奇异H-矩阵在计算数学、动力系统理论以及神经网络等众多领域都有重要的应用,但是其判定却比较困难。近年来很多学者对其作了较深入的研究,并给出了一些重要结果[1-9]。例如,文献[1]给出了非奇异H-矩阵的简捷判据;文献[3]给出了非奇异H-矩阵的迭代判定方法,改进了文献[1]的结果。本文给出一类非奇异H-矩阵的新迭代判定准则,从而推广了文献[1-4]的结果。
为叙述方便,引入下列记号:
Cn×n表示 n×n阶复矩阵的集合;
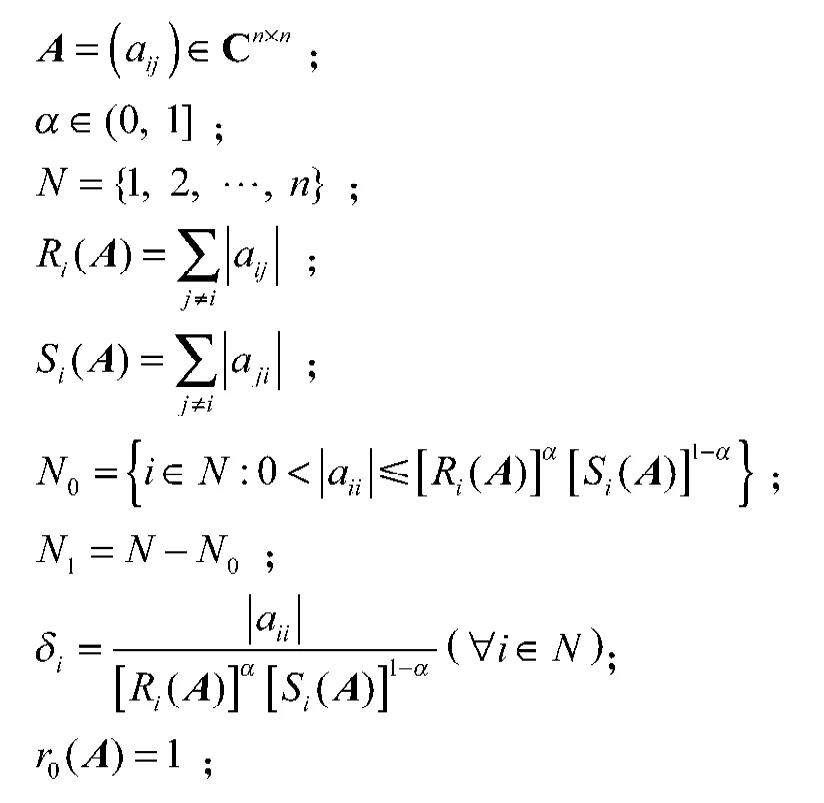

2 主要结果
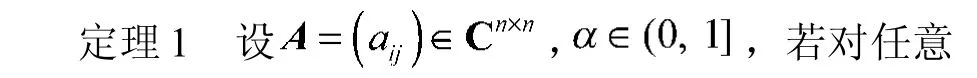




3 数值算例

[1]黄廷祝.非奇异H矩阵的简捷判据[J].计算数学,1993,15(3) :318-328.HUANG Tinzhu.Some Simple Determinate Conditions for Nonsingular H-Matrix[J].Mathematica Numerica Sinica,1993,15(3) :318-328.
[2]干泰彬,黄廷祝.非奇异H矩阵的实用充分条件[J].计算数学,2004,26(1) :109-116.GAN Taibin,HUANG Tingzhu.Practical Sufficient Conditions for Nonsingular H-Matrices[J].Mathematica Numerica Sinica,2004,26(1) :109-116.
[3]王峰.非奇异H-矩阵判定的迭代准则[J].安徽大学学报(自然科学版),2012,36(6) :16-20.WANG Feng.New Iterative Codes for Nonsingular HMatrices[J].Journal of Anhui University(Natural Science Edition),2012,36(6) :16-20.
[4]黄泽军,刘建州.非奇异H-矩阵的一类新迭代判别法[J].工程数学学报,2008,25(5) :939-942.HUANG Zejun,LIU Jianzhou.New Iterative Criteria for Nonsingular H-Matrices[J].Chinese Journal of Engineering Mathematics,2008,25(5) :939-942.
[5]BERMAN A,PLEMMONSR J.Nonnegative Matrix in the Mathematical Sciences[M].New York:Academic Press,1979 :24-83.
[6]周伟伟,徐仲,陆全,等.非奇H-矩阵细分迭代判定准则[J].数值计算与计算机应用,2011,32(4) :293-300.ZHOU Weiwei,XU Zhong,LU Quan,et al.Subdivided and Iterative Codes for Nonsingular H-Matrices[J].Journal on Numerical Methods and Computer Applications,2011,32(4) :293-300.
[7]张俊丽,韩贵春.一类非奇异H-矩阵的迭代判定准则[J].河南科技大学学报(自然科学版), 2016,37(1) :88-91.ZHANG Junli,HAN Guichun.Iterative Criteria for a Kind of Nonsingular H-matrices[J].Journal of Henan University of Science & Technology(Natural Science), 2016,37(1) :88-91.
[8]薛媛,刘建州.H-矩阵的一类实用递进判别法[J].湘南学院学报,2014,35(2) :1-4.XUE Yuan,LIU Jianzhou.A Type of Practical Progressive Criteria for Identifying H-Matrices[J].Journal of Xiangnan University,2014,35(2) :1-4.
[9]丁碧文,刘建州.广义严格对角占优的充分条件[J].高等学校计算数学学报,2009,31(4) :310-318.DING Biwen,LIU Jianzhou.Sufficient Conditions of Generalized Strictly Diagonally Dominant Matrix[J].Numerical Mathematics:A Journal of Chinese Universities,2009,31(4) :310-318.
(责任编辑 :邓光辉)
An Iterative Method for the Determination of Non-singular H-Matrices
ZHANG Junli
(School of Mathematics,Inner Mongolia University for the Nationalities,Tongliao Inner Mongolia 028043,China)
Although the non-singular H-matrix has found its wide applications nowadays, the determination of its practical use seems rather difficult.An improvement and its promotion have been made of the relevant results based on the analysis of the relations between -diagonally dominant matrices and non-singular H-matrices, with the criteria of the latter one accordingly determined, thus further verifying the validity of these criteria with numerical examples.
non-singular H-matrix;-diagonally dominant matrix;irreducible;non-zero elements chain
O151.21
A
1673-9833(2016)04-0074-04
10.3969/j.issn.1673-9833.2016.04.014
2016-05-30
国家自然科学基金资助项目(11361038),内蒙古自然科学与技术研究基金资助项目(NJZY13159)
张俊丽(1980-),女,山东菏泽人,内蒙古民族大学讲师,主要研究方向为数值代数,E-mail:jl_zhang7706@163.com

