基于特征值分析的雷达脉冲波形估计及性能分析

解辉，程呈，张宏伟

（军械工程学院，石家庄050003）

基于特征值分析的雷达脉冲波形估计及性能分析

解辉，程呈⋆，张宏伟

（军械工程学院，石家庄050003）

雷达侦察接收机往往侦收到多个受噪声污染的目标雷达脉冲，如何从噪声中提取雷达脉冲波形，是现代雷达侦察信号处理中的一个重要内容。提出了一种基于特征值分析的雷达脉冲波形估计算法，该算法通过对脉冲协方差矩阵的特征值分析，给出了一种利用特征向量估计脉冲波形的方法，并理论分析了其估计性能。算法适应于任意形式脉冲波形，且不受各脉冲初始相位的影响。理论分析和仿真结果说明算法能够在较低信噪比环境下恢复脉冲信号波形。

特征值分析，脉冲波形，协方差矩阵，特征向量

0　引言

现代雷达广泛采用复杂体制信号和多域调制［1-2］，同时其频率范围也随之扩展，面对目前日益增加的密集、复杂的电磁环境，仅靠测量传统的脉冲参数（载频、脉冲宽度、脉冲幅度、到达时间、到达角等）很难满足当前雷达情报侦察处理的需要。因此，基于细微特征的雷达个体识别、辐射源指纹识别等成为目前电子对抗领域一个新的研究热点［3-11］，尤其是在各种低截获概率（Low Probability of Intercept，LPI）雷达应用日益广泛的背景下，完成脉冲采样数据的处理，测量脉冲的脉内参数以及提取其细微特征成为雷达侦察信号处理的重要方向。然而，雷达脉冲脉内参数测量，辐射源细微特征提取并完成辐射源个体识别需要较高的信噪比［3，6，9］，这在实际的电子侦察中往往难以满足。因此，研究雷达脉冲波形的估计方法，提高信号的信噪比成为一个亟需解决的问题。

雷达脉冲是一种周期出现的信号，利用脉冲的这种周期性实现数据积累是一种直观的想法，很多检测和参数估计方法采用了这种思想［15］。然而，由于很多雷达脉冲是非相参的，在估计雷达脉冲波形时这种直观的数据积累将不再有效。本文利用雷达脉冲的周期性，研究一种实现脉冲波形积累的新方法，其处理增益接近相参积累。

1　信号模型

设第i个雷达脉冲的复信号模型为

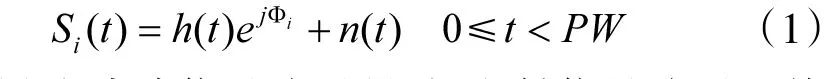
其中h（t）为脉冲信号波形（包括发射信号波形及其与接收机的卷积等），Φi为第i个脉冲的初相，j为虚数单位，n（t）为方差为σn2的零均值高斯噪声，PW为脉冲宽度。

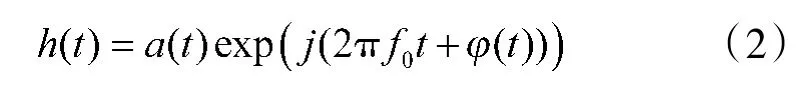
其中，a（t）为脉冲的幅度调制函数，φ（t）为脉冲信号的相位调制函数。

对于不同调制类型的雷达脉冲具有不同形式的a（t）或φ（t）。例如，对于常规单载频信号，

对于线性调频信号，

其中，k为调制斜率，且t≤PW。

对于相位编码信号，

其中Cd（t）为相位编码函数，其码元宽度小于脉冲宽度PW。

对于其他脉冲信号a（t）和φ（t）各有不同的形式，本文算法与其无关，在此不再逐一列举。

在进行脉冲波形估计之前，本文先作如下假设:

1）噪声n（t）与信号不相关，即有

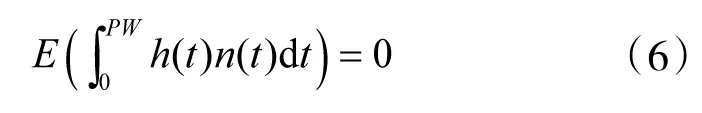
2）信号均值为零，即信号的能量可以表示为

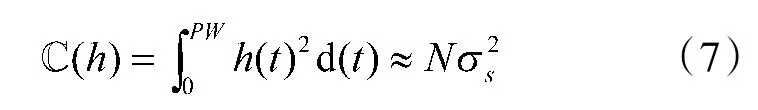
2　脉冲波形估计算法

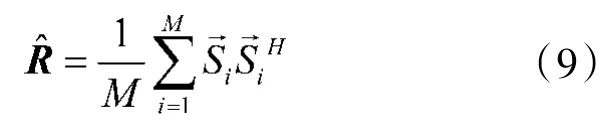
将信号模型式（1）代入上式，并结合式（6）可得

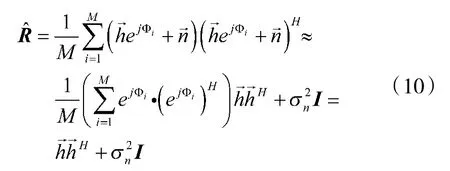
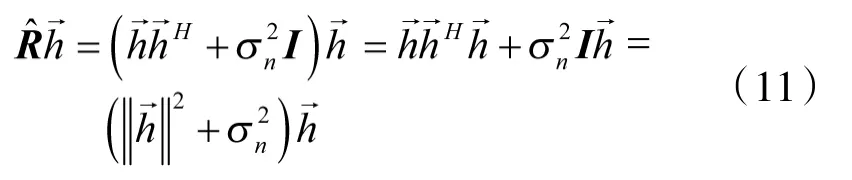
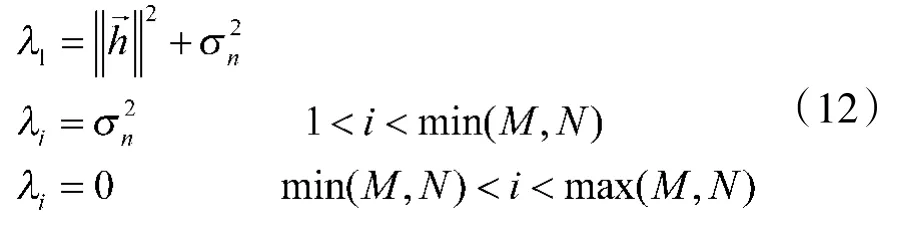
其中N为每个脉冲的采样点数。不失一般性，本文后续分析将以N＞M为例进行。

由式（12）可得信噪比ρ的估计值

通过以上分析可以得出结论:雷达脉冲的协方差矩阵有一个较大特征值，该特征值对应的特征向量为脉冲波形。因此，可以利用协方差矩阵的特征向量估计雷达脉冲波形。

3　算法性能分析

下面利用矩阵的扰动理论［16］，分析脉冲波形的估计误差。对于矩阵扰动下的特征值和特征向量分布具有以下结论［17］

其中，ui为对应特征值的正交归一化特征向量。上述各式说明特征值为有偏估计，特征向量为无偏估计。

如果每个脉冲的采样点数为N，则有

将上式代入式（18），且M较大时有

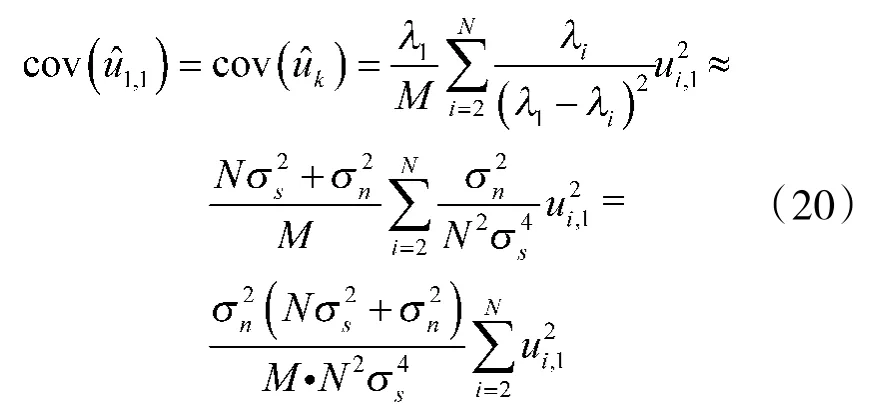
其中ui，j为特征向量ui的第j个分量。

因为u1为一确定信号，所以的能量可以表示为

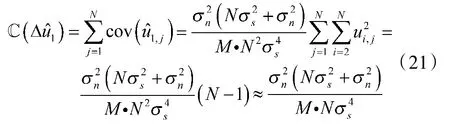
同时，归一化的信号能量为

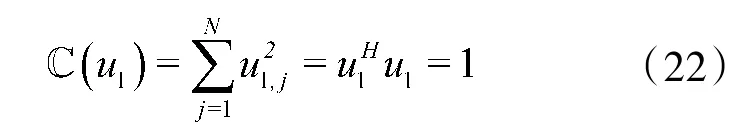
所以，输出信噪比为

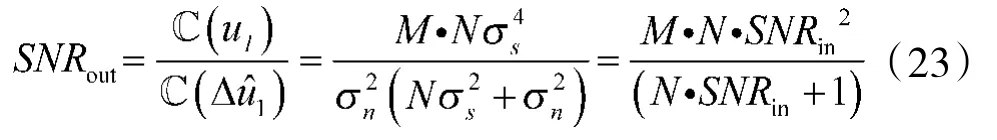
以dB为单位表示为

由上式可以看出，估计波形的信噪比除了与输入信号信噪比有关还与积累脉冲个数和每个脉冲内的采样点数有关。

4　仿真分析

本文以线性调频脉冲和二相编码脉冲为例对本文的估计方法进行仿真验证。线性调频信号的起始频率为20 MHz，调制带宽为10 MHz，脉冲宽度为10 us，即调制斜率为1 MHz/us；二相编码信号采用13位Barker码，脉冲宽度也为10 us，两种信号的采样频率均为100 MHz。

图1给出了利用50个脉冲估计协方差矩阵时的部分特征值。图1（a）是-3 dB线性调频信号对应的特征值，图1（b）是0 dB二相编码信号对应的特征值。由图1可以看出，协方差矩阵存在一个较大特征值。图2给出了线性调频信号波形估计前后的时频分布。由图中可以看出，估计后波形的噪声干扰明显降低。

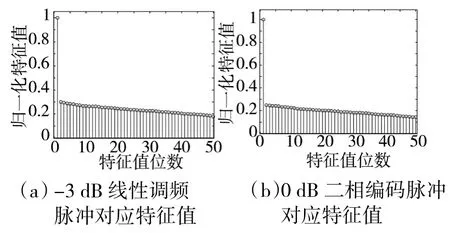
图1　脉冲协方差矩阵特征值

图2　波形恢复前后线性调频信号的时频图

图3和图4分别给出了0 dB二相编码信号原始信号和估计信号的波形与时频图，仿真脉冲个数为50个。由图中可以看出，估计后的波形明显改善，时频图中的噪声明显减少。

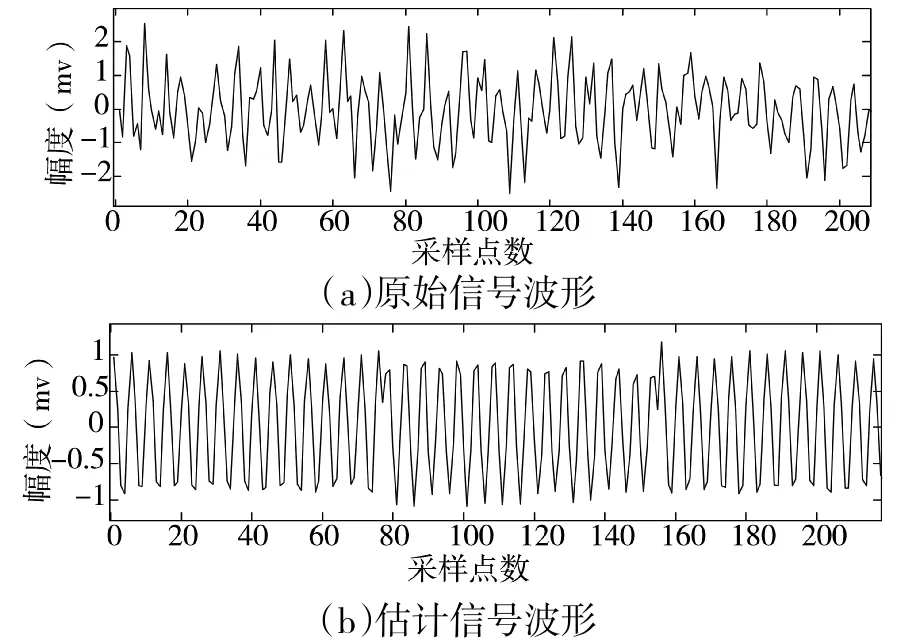
图3　估计前后二相编码信号波形

图4　波形恢复前后二相编码信号的时频图

下页图5给出了不同信噪比下估计波形输出信噪比的理论值和仿真结果，仿真采用二相编码脉冲，每个脉冲采样点数为1 000，脉冲个数为50，蒙特卡罗仿真次数为100。由图中可以看出，在输入脉冲信噪比为-6 dB时输出信号信噪比超过10 dB，说明本文算法具有较高的处理增益。另外，仿真结果验证了理论分析结果的正确性。

图5　波形估计输入输出信噪比

5　结论

本文给出了一种基于特征值分析的雷达脉冲波形估计方法，该方法利用了信号协方差矩阵的特征向量实现了脉冲波形的估计。本方法具有3个突出特点，一是能够适应任意形式的波形；二是适应相参和非相参雷达；三是信噪比适应能力强，在积累50个脉冲时可以将-6 dB信噪比的脉冲恢复到10 dB。理论分析和仿真结果证明了该方法能够在较低信噪比环境下恢复脉冲波形。

［1］JAMES D T.Ultrawideband radar progress［C］//IEEE Radar Conference，2012:190-195.

［2］杨建宇.雷达技术发展规律和宏观趋势分析［J］.雷达学报，2012，1（1）:19-27.

［3］JIANG H Q，GUAN W S，AI L.Specific radar emitter identification based on a digital channelized receiver［C］//2012 5th International Congress on，2012.

［4］LIU M W，JOHN F.Nonlinearity estimation for specific emitter identification in multipath channels［J］.IEEE Transactions on Information Forensics and Security，2011，6（3）: 1076-1085.

［5］LIU H J，LIU Z，JIANG W L，et al.Approach based on combination of vector neural networks for emitter identification［J］.IET Signal Processing，2010，4（2）:137-148.

［6］张国柱，黄可生，姜文利，等.基于信号包络的辐射源细微特征提取方法［J］.系统工程与电子技术，2006，28（6）: 741-742.

［7］韩韬，周一宇.雷达信号的扩散特征及其在特定辐射源识别中的应用［J］.电子学报，2013，41（3）:502-507.

［8］王磊，史亚，姬红兵.基于多集典型相关分析的雷达辐射源指纹识别［J］.西安电子科技大学学报（自然科学版），2013，40（2）:164-171.

［9］旷平昌，王杰贵，罗景青.基于脉冲样本图和Vague集的雷达辐射源识别［J］.宇航学报，2011，32（7）:1639-1644.

［10］马爽，柳征，姜文利.基于幅度变化点检测的多功能雷达脉冲列解析方法［J］.电子学报，2013，41（7）: 1436-1441.

［11］李程，王伟，王雪松.基于盒差分滤波器的脉冲检测算法［J］.系统工程与电子技术，2013，35（8）:1615-1619.

［12］曹磊，张剑云，王小平，等.基于最小均方误差的认知雷达估计波形设计方法［J］.探测与控制学报，2013，35（4）:63-67.

［13］王方秋，张小飞.脉冲超宽带系统中基于改进传播算子算法的TOA和DOA联合估计［J］.电子与信息学报，2013，35（12）:2954-2959.

［14］隋凯凯，李宏，李欣欣.杂波加噪声环境下MIMO雷达检测性能分析［J］.计算机系统应用，2013，22（9）: 230-233.

［15］高峰，杨进华，姜成昊，等.非扫描激光雷达系统的多脉冲积累信噪比分析［J］.激光与光电子学进展，2012，49（5）:1-6.

［16］戈卢布G H，范洛恩G F（著）.矩阵计算［M］.袁亚湘，译北京:科学出版社，2001.

［17］BOUDER C，AZOU S S，BUREL G.Performance analysis of a spreading sequence estimator for spread spectrum transmissions［J］.Journal of Franklin Institute，2004，341: 595-614.

Waveform Estimation of Radar Pulses Based on Eigenanalysis and Performance Analysis

XIE Hui，CHENG Cheng⋆，ZHANG Hong-wei
（Ordance Engineering College，Shijiazhuang 050003，China）

The problem of waveform estimation of radar pulses which badly contaminated by noise is addressed in this paper.A new waveform estimation method is proposed based on eigennalysis and its performance is also analyzed.By eigenvalue-decomposition of the covariance matrix，the algorithm gives a waveform estimation method by eigenvector.The algorithm adapts to waveform of pulses with any shapes，and it is not limited by initial phases of the pulses.This method also can estimate the waveform even the

signal is below the noise level.The theoretical analysis and simulation results indicate the efficiency of our algorithm.

eigenanalysis，waveformofpulse，covariancematrix，eigenvector

TN911.22

A

1002-0640（2016）06-0177-04

2015-05-09

2015-06-19

解辉（1983-），男，河北易县人，博士，讲师。研究方向：雷达、通信信号处理、信道编码识别技术等。

程呈⋆（1991-），男，山西运城人，博士研究生。研究方向：雷达信号盲分离，雷达信号处理。