刚接板法在单箱多室箱梁偏载系数计算中的应用
孙 恒
(山西省交通科学研究院,山西 太原 030006)
随着经济的发展,交通量日益增大,路网密度越来越大,随之出现了大量的互通桥梁,这些桥梁多为宽跨较大的宽桥,在城市建设中,为满足日益增大的车流量,中小跨径桥梁也多为宽梁桥。其桥梁宽度与跨度相近,甚至要超过跨径,因此结构的受力性能及特点也更复杂。单箱多室箱梁结构由于其整体性好,受力性能合理,结构美观,广泛用于宽桥。
单箱多室箱梁桥属于空间结构受力体系,对其进行精确的受力分析一般要采用实体建模分析,实际工程中进行精确受力分析的意义不大,加之实体建模比较繁琐,因而很少采用实体建模进行分析,通常采用简化计算方法进行工程设计计算。
1 单箱多室箱梁偏载系数简化计算方法
单箱多室箱梁属于空间结构体系,在偏心荷载作用下会产生纵向弯曲、扭转、畸变和横向挠曲4种基本变形状态,其整体受力属于空间结构体系。设计经验表明,由于箱形截面的抗扭刚度大,由扭转引起的应力通常比平面弯曲引起的应力小很多,且在实际工程设计中进行精确分析的必要性不大,因而设计中一般采用平面杆系结构进行简化,只考虑纵向弯曲;扭转、畸变和横向挠曲的影响则通过偏载增大系数来考虑。偏载系数可以用单箱多室箱梁控制截面偏心荷载作用下的梁体最大挠度与该控制截面的挠度平均值之比来表示。目前在我国计算偏载系数简化计算方法有偏心压力法、修正的偏心压力法和荷载增大系数法等[1]。
荷载增大系数法和偏心压力法忽略了主梁的抗扭刚度并认为主梁横向绝对刚性,因此计算结果明显偏大。修正的偏载系数计算公式大多是对现有的计算公式进行修正,并且算法并不一致,对公式也没有进行大量的数值模拟和实桥偏载试验进行验证,研究结果的可靠性无法保证。
目前工程设计当中对于宽箱梁设计计算可采用的做法是建立空间杆系模型或者建立实体单元空间有限元模型来分析,前者计算精度一般,但是能满足工程设计需要,但是其对原结构进行了面目全非的简化,大量几何参数要预先计算准备,前后期均需要大量的人工进行数据处理,需要设计人员有足够的耐心和细致的工作,人为偏差较难避免[2];后者计算精度高,但是建模繁琐,计算时间长,且结果不能直接用于相关规范验算。另外在实际工程中,很多设计人员常常采用经验值1.15的固定值[3],建立单梁模型进行计算,仅在验算结果中用富裕量近似考虑宽箱梁扭转的影响,这就造成了设计质量参差不齐,桥梁耐久性无法保证。
本文通过对传统多梁式刚接板(梁)法的计算原理进行研究,提出适用于单箱多室箱梁偏载系数计算的刚接板(梁)法,以期为今后同类型桥梁设计提供借鉴和参考。
2 刚接板(梁)法计算原理
2.1 传统刚接板(梁)法
传统刚接板(梁)法是在针对于多梁式铰接板计算理论的基础上,在接缝处补充引入赘余弯矩m如图1所示,建立了横向刚性连接特点的正则方程[1]。
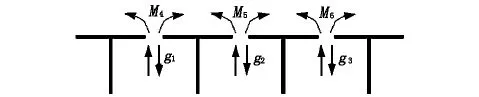
图1 多梁式刚接板(梁)法计算图式

对于系数矩阵[δij]对于仅涉及 g1,g2,g3和相应位移的系数,与铰接板法完全一样,即:
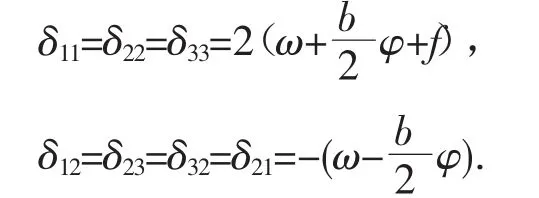
对于仅涉及赘余弯矩M4、M5、M6和相应转角的系数,有:

通过对图1进行分析,还可以写出:
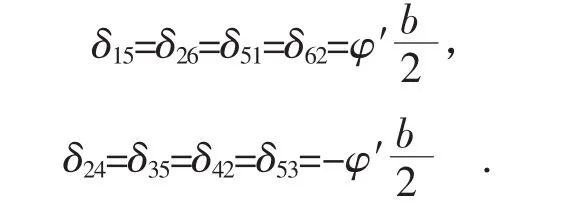
当单位正弦荷载作用于1号梁中心线上时,可得荷载向量:δ1p=ω,其余系数均为0,通过求解正则方程[1]即可得到接缝处的赘余力值,进而可以求得横向分布系数。
2.2 刚接板(梁)法在单箱多室箱梁偏载系数计算中的应用
如图2所示单箱五室箱梁,按照刚接板梁法将箱梁沿腹板中心线划开,并在切口处补充赘余力。
根据力法原理此计算图式的正则方程与多梁式刚接板法一致。

图2 单箱多室箱梁刚接板(梁)法计算图式
其中系数矩阵、荷载向量、以及 ω、φ、f、φ'、τ计算公式与多梁式刚接板法均相同。在计算截面特性的时候对于沿腹板中心线划开每个小工字型梁,截面抗弯惯性矩可以按照实际截面尺寸进行计算,截面抗扭惯性矩和横桥向截面特性不能简单按照开口截面进行计算,应该按照闭口截面进行计算。
3 实例分析
本节通过一单箱四室箱梁为例,具体介绍刚接板(梁)法的计算步骤,并与实体计算结果对比。
某公路预应力钢筋混凝土单箱四室箱梁桥,跨径20 m,单箱顶宽19.5 m,底宽15.5 m,两侧悬臂长2.0 m,端部厚0.18 m,根部厚0.5 m,箱梁顶底板厚度均为 0.25 m,腹板厚度 0.45 m,腹板中心距3.761 8 m,C50现浇混凝土,泊松比0.425。该桥设计荷载为双向四车道公路-Ⅰ级汽车荷载,车辆加载形式按照《公路桥涵设计通用规范》(JTG D60—2004)的规定布置。具体尺寸及加载车辆实际作用的位置,见图3所示。

图3 箱梁横断面尺寸及车辆作用位置图(单位:cm)
根据前述箱梁单元划分方法,沿腹板间将单箱四室截面箱梁切开成工字梁组成的结构,如图4所示。

图4 箱梁划分示意图
当位于图4所示的号梁顶面时,通过计算可得切口处竖向赘余力为:

1号梁影响线竖标求解如下:


画出1号梁的影响线如图5所示。
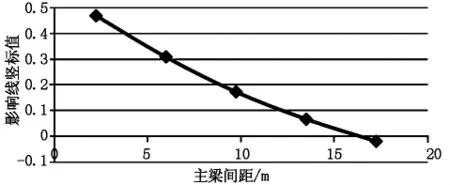
图5 采用刚接板(梁)法计算的边腹板横向分布影响线
按照加载车辆实际作用的位置及影响线竖标值计算该箱梁偏载系数1.269。
采用MIDAS/FEA有限元分析软件对该箱梁进行受力分析。混凝土弹性模量E取3.45×104N/mm2,泊松比γ=0.425,混凝土容重取25 kN/m3。将主桥每跨纵桥向划分为40等分,每个单元长0.5 m,主梁采用实体单元。对节点自由度施加位移约束来模拟支座与主梁的连接。
在弹性分析中,主梁荷载分配大小与其挠度值呈正比关系,据此将求得主梁中跨、边跨跨中截面各个腹板下缘挠度值以及中跨、边跨跨中截面的偏载系数计算结果汇于表1。

表1 实体建模计算偏载系数结果汇总 mm
通过对比可以发现:
a)由表1可得单箱多室宽箱梁边跨偏载系数略大于中跨,差值为3.5%左右。
b)由表1与刚接板梁法计算结果对比可以发现,刚接板梁法结果与实体计算结果吻合度较好,刚接板梁法结果介于实体边跨和中跨计算结果之间,具体差值对于边跨差值-2.16%,对于中跨差值+1.36%。
c)对于单箱多室宽箱梁桥,采用刚接板(梁)法计算偏载系数结果略小,但精度能够满足工程设计要求,实际应用时将计算结果适当放大偏保守计算。
d)当箱室增加时,对于公式(1),其正则方程中的系数矩阵成阶数增加,每增加一个箱室,系数矩阵阶数增加2阶,实际应用时可以编成计算程序,能大大简化计算过程。
4 结论
单箱多室宽箱梁桥在今后桥梁建设当中会应用越来越广泛,而规范对此并未进行详细规定,而且关于单箱多室宽箱梁桥偏载系数计算还没有比较成熟的理论公式,采用实体建模进行计算分析十分繁琐,必要性也不大。本文采用刚接板梁法对单箱多室宽箱梁桥偏载系数进行计算,通过与实体模型对比可以发现计算精度能够满足工程实际,实际应用中可以将正则方程编程计算程序,能大大简化计算过程,可以为单箱多室宽箱梁桥设计提供便利。

