基于排队论的Web服务社区最优服务数设置*

何晨翔， 付晓东， 刘 骊， 刘利军， 黄青松

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)



基于排队论的Web服务社区最优服务数设置*

何晨翔， 付晓东， 刘 骊， 刘利军， 黄青松

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

Web服务社区是将功能类似的Web服务集中到一起为用户提供服务，当大量用户同时访问社区时，会出现排队现象。用户在社区中排队时会占用一部分资源，从而会产生一部分额外的成本。为此研究了如何设置最优的服务数使得这部分的额外成本最小。给出Web服务社区的定义，将在服务社区中排队的问题映射成排队论问题，确定排队模型为M/M/n。计算在稳定状态时用户的排队长度，得出在社区中排队的用户数量。结合Web服务社区中的成本因素确定成本函数，结合经济学中的边际分析法求出最佳的服务数。实验表明：该方法可以有效地找出最优的服务数，且效率较高。

Web服务； Web服务社区； 排队论； 边际分析法

0 引 言

近年来，随着互联网上Web服务的数量的不断增长，面向服务计算SOC(service oriented computing)成为主流的计算范型。Web服务是一种崭新的、模块化、自描述的分布式计算模型，采用可扩展标记语言(XML)定义了Web 服务协议栈， 通过SOAP(simple object access protocol)、UDDI(universal description，discovery ,and integration) 、BPEL4WS(business process execution language for Web integration)和WSFL(Web services flow language)等协议，提供面向互联网应用的统一服务绑定、发现、及注册集成调用机制[1]。

随着Web服务的数量不断增加，有学者就提出了Web服务社区的概念，文献[2]指出Web服务社区是由大量的Web服务组合成的，其中，Web服务功能相似且具有不同的非功能的特性。例如，来自不同的提供者或QoS不同。由于在一个Web服务社区中的服务具有相同领域兴趣，因此，在领域QoS评价上有最多的共同点，例如，有天气查询功能的服务共同组成天气查询服务社区。Web服务社区是动态生成的，通过特定场景和协议建立和拆除，集结方式和P2P网络类似[3]。所有的领域对应的社区中都有一个主Web服务，它储存该服务社区中所有Web服务的相关信息，并拥有优于社区其他Web服务的各种参数。主Web服务基于语义聚集有相同原子功能的从Web服务。生成方式是双向的，主服务定期到UDDI查询是否有符合社区要求的节点，或由新节点向主服务提出加入请求，主服务认证后加入[4～6]。

Web服务社区的概念提出后，文献[7,8]提出了功能相似的Web服务被分组后如何更容易的在互联网上被发现的问题。然而这些研究同样没有研究当Web服务社区中有大量的服务的情况下。文献[9]中作者提出了在社区中如何有效的定位Web服务。作者提出在不同的环境下对服务的描述不同于语义层的意思，所以传统的按照关键字去搜索是在Web服务的一个很小的范围。然而该研究没有考虑到当Web服务社区中的服务数越来越多的情况。当社区中服务或者用户过多时作者提出的这种方法就会出现一些错误的结果。

综上所述，国内外对Web服务社区进行了大量的研究。对Web服务社区的研究多数是集中在Web服务的选择和Web服务社区的结构等问题上，很少有涉及到Web服务的社区的成本问题和社区中Web服务数的设置问题。同时绝大多数研究没有考虑到当社区中有大量的Web服务和大量用户访问社区的情况。本文研究的问题首先就是考虑到社区中有大量的Web服务而且在一个时间段会有大量用户访问服务社区。在这种情况下会出现排队现象，然后本文结合了排队论和边际分析法对Web服务社区的运行成本进行了研究。

1 Web服务社区的排队模型

1.1 Web服务社区

随着Web服务的不断增加，出现了Web服务的组合形式。文献[4]给出了Web服务社区的相关概念和操作。这里用图形表示出Web服务社区的体系结构。如图(1)所示。图1 包含了2 类服务：一种是社区服务，另一个是普通Web 服务。图1中的社区也是Web服务的一种，这类Web服务规定了某些功能接口，它自身不去实现这类功能，其功能由具体的Web 服务实现，图1中虚线箭头表示服务的发布，实线箭头表示Web 服务实现的相应社区的功能，类似于面向对象中超类和子类的关系。

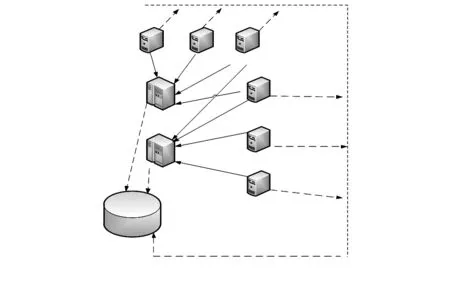
图1 Web服务社区体系结构Fig 1 Architecture of Web service community

在Web服务社区的体系结构下，图2给出了Web服务社区是如何给用户提供服务。首先Web服务实现社区的接口然后在社区中注册，然后Web服务去注册中心进行注册。当用户要调用Web服务时，用户首先到注册中心查找相关信息，注册中心会给出用户所需要的Web服务所在的社区。用户直接到对应的社区中查找自己需要的Web服务。图2中也能看出社区中可能存在多个用户访问同一个Web服务，这里用户要是调用相对应的Web服务时就必须在社区中排队。

图2 Web服务与用户的交互过程Fig 2 Interaction process of Web service with user

1.2 问题描述

Web服务社区在给用户提供服务时服务的数量是一定的，但是在一个时间段到达社区的用户不是不确定的。当大量用户到达社区时就会出现社区不能给每个用户提供服务的情况。这样用户就会在社区中排队，等待服务。当大量用户在社区时会对社区产生一些如人力资源、网络资源、系统资源等的成本。这些成本会对整个社区的运营产生一定的成本。这里要解决的两个重要的问题。第一是如何确定社区中排队的用户数，第二如何设置服务数使得社区的运营成本最少。

为了确定社区中排队的用户数，要先确定Web服务社区中的排队模型，本文作者研究用户服从泊松流到达服务社区。社区给用户提供的服务时间服从负指数分布。各个服务之间都是独立工作的。本文讨论的服务社区在提供服务时没有限制顾客来源和系统容量。

定义1 设M/M/n系统的输入过程{N(t),t≥0}为参数 的泊松过程，即到达间隔时间序列{Jk,k≥0}为i.i.d随机变量序列，且J1～Γ(1,λ)。服务机构有n个(n≥1)服务台，每个服务独立工作，且具有相同分布的服务时间B，B～Γ(1,μ)，即顾客的服务时间序列{Bk,k≥1}为i.i.d随机变量序列，且B1～Γ(1,μ)并设{Bk,k≥1}与{Jk,k≥1}独立。

由定义1知道在M/M/n排队模型中，顾客是服从泊松分布到达系统的，服务给用户提供服务是服从负指数分布的，所以，这里选择M/M/n。在确定好排队模型后可以利用排队的知识论得出在社区中排队的用户数。

Web服务社区中的排队模型为M/M/n,当用户按照泊松流到达系统时，社区不能给每个用户提供服务，所以在M/M/n模型排队下进行排队。排队会消耗一些成本，把这些资源统称为排队成本。社区在给用户提供服务时，服务本身也有其成本。在设置不同的服务数时，整个服务社区的运营成本不同。本文研究的重点是如何在服务社区中设置最优的服务数使得Web服务社区在低成本下运营。

定义2 记w为排队成本，服务的成本为a，社区提供的服务数c,系统中用户排队的长度为Ns。得到Web服务社区的成本函数

g(c)=ac+wNs

(1)

在此函数中，要计算出最优的服务数c，使得成本函数函数最小。这里排队成本、服务成本都是从实际生活中能得到，现在需要计算的就是系统中排队的用户数Ns。

1.3 Web服务社区的排队用户数

在M/M/n模型下，Web服务社区中可以同时提供c(c>1)个服务，用户服从泊松流到达，到达强度为λ。社区给用户提供时没有一个统一的时间，在M/M/n模型下社区给用户提供的服务时间服从负指数分布，强度为μ。本文讨论的服务社区在提供服务时没有限制顾客来源和系统容量。

(2)

式中

(3)

当系统处于平衡状态下，系统中的等待对长Ns是排队对长Nq与正在被服务的顾客数Nc之和。记作

Ns=Nq+Nc

(4)

当ρc<1时，系统中排队长度Nq为

(5)

当系统在平衡时正在被服务的顾客数Nc为

Nc=E[Nc]=ρ

(6)

所以,可以得到在系统在平衡状态时系统的平均顾客数

(7)

2 边际分析法

边际分析法是对某种变量的增加以及由其引起的总量的变化进行统筹考虑来寻求最优解。[10]。本文解决的问题是离散的，所以不能使用微积分原理。边际分析法在解决离散问题上的基本思想是追加下一个单位，然后两两比较，选择相对优的结果，然后再和其他的比较，直到选择最优的结果[11]。

本文利用边际分析法在解决离散问题上的思想。由定义(2)可知社区成本函数为g(c)=ac+wNs。由于c 是离散的，所以可以逐渐的增加c的值，所以可利用边际分析法求出最优的c。即c要同时满足

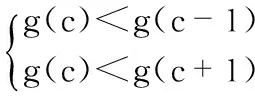
(8)

整理得到

(9)

在上式中，通过不断增加n的值来确定是否满足不等式。如果c等于某个值时满足不等式则将c的值输出，即得出c是Web服务社区中提供的服务数使得整个服务社区的成本最小。算法如下：

INPUT:Webservicesetλ,μ,w,a

OUTPUT:Minc

1if(ρc<1)

2Computep0(ρ0)

3 Ns(pc)← Nq(pc) + Nc(pc)

4forc=1to∞

5ifMincexist

3 实验结果与分析

由于现存的Web服务社区比较少，无法获得真实的数据，本文模拟银行排队的模型，c采集银行排队模型的数据。实验中，设置不同的λ，μ，w，a值，然后利用第三节研究的方法进行验证。

实验首先以Eclipse为开发工具，Java为开发语言，在JDK开发环境下进行实验的。实验中设置λ，μ，w，a值，这里令λ，μ不变，让w，a不断的变化，在这种情况下找出最优的c值。可以得到图3。

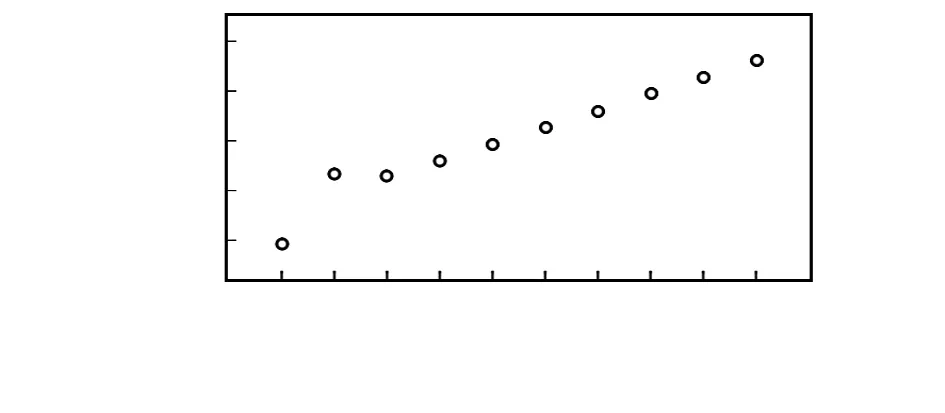
图3 服务数与社区成本的关系Fig 3 Relationship between service number and community cost

图3中,随着服务数不断增大时，整体的成本会随着增大。当c=1时，成本值为负数所以舍弃。但是在c=3的时，成本出现了最小值。所以使用边际分析法可以找到最优的服务数c。

为了方便看出二者的差异，实验中首先让参数μ变化，然后比较二者的运行时间。再令λ变化，其他参数不变。可以得到图4、图5。

图4 不同μ下边际分析法与非边际分析法的运行时间关系Fig 4 Running time relationship between marginal analysis method and non marginal analysis method with different μ

由图4可知可以看出，使用边际分析法的运行时间明显要小于非边际分析法，并且使用边际分析法的运行时间比较稳定，运算效率要高。

图5 不同λ下边际分析法与非边际分析法的运行时间关系Fig 5 Running time relationship between marginal analysis method and non marginal analysis method with different λ

由5图可以看出，使用边际分析法的运行时间明显要小于非边际分析法。

实验中由于不同PC机的CPU处理能力不同得到的运行时间也会不同，但是这里可以保证的是在不同的PC机上运行使用边际分析法所用的运行时间会比没有使用边际分析法的运行时间要短。

4 结 论

针对Web服务社区中最小成本运营的服务设置，本文首先，确定服务社区中用户排队的模型为多服务窗M/M/n。在M/M/n模型下，结合排队论的知识确定在排队稳定情况下服务社区中用户排队的长度。然后结合Web服务社区中的成本因素确定成本函数，并利经济学中的边际分析法进行计算分析，找出最优的服务数。

通过实验验证，使用边际分析法可以有效的找出最优的服务个数，实验也说明了使用边际分析法要比不使用边际分析法更有效率。下一步的研究是在M/M/n模型下的排队时间最短。

[1] Guo D K,Ren Y,Chen H H,et al.A QoS-guaranteed and distri-buted model for Web service discovery[J].Journal of Software,2006,17(11):2324-2334.

[2] Bentahar J,Maamar Z,Benslimane D.Using argumentative agents to manage communities of web services[C]∥Proceedings of the 21st International Conference on Advanced Information Networking and Applications Workshops,Washington D C,USA:IEEE Computer Society,2007:588-593.

[3] Li Ruixuan,Zhang Zhi,Wang Zhigang,et al.WebPeer:A P2P-based system for publishing and discovering Web services[C]∥Proc of the 2005 IEEE International Conference on Service Computing，Washington D C,USA:IEEE Computer Society,2005:149-158.

[4] Maamar Z,Lahkim Mohammed,Benslimane Djamal.Web Ser-vices Communities-Concepts & Operations[C]∥Proc of The 3rd Int’l Conf on Web Information Systems and Technologies,WEBIST’07,2007:323-327.

[5] Ali S,Omer R,Rashid A A.An extended registry for Web ser-vices[C]∥Proceedings of the Service Oriented Computing:Models,Architectures and Applications,SAINT—2003 IEEE Computer Society,Orlando,Florida,2003:85-89.

[6] Al-Masri E,Mahmoud Q H.Crawling multiple UDDI business registries[C]∥Proceedings of the 16th International Conference on World Wide Web,ACM,2007:1255-1256.

[7] Yahyaoui H,Maamar Z,Lim E,et al.Towards a community-based,social network-driven framework for Web services management[J].Future Generation Computer Systems,2013,29(6):1363-1377.

[8] Subramanian S.Highly-available Web service community[C]∥2009 the Sixth International Conference on Information Technology:New Generations,IEEE Computer Society,2009:296-301.

[9] Wang Lei,Liu Fangfang,Yu Jie,et al.Search of Web service based on community[C]∥2012 IEEE The 12th International Conference on Computer and Information Technology,2012:1072-1075.

[10] 李静江,刘治兰.管理经济学[M]．北京：华文出版社,2002.

[11] 邝美瑕.关于离散型随机变量的边际分析决策问题的探讨[J]．武汉粮食工业学院学报,1992(4):49-55.

Research on set of the optimal service number of web service community based on queue theory*

HE Chen-xiang， FU Xiao-dong， LIU Li， LIU Li-jun， HUANG Qing-song

(Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

Web service community collect similar Web services to provide services to users.There will be queuing phenomenon when a large number of users access to the community at the same time.Users will take up a portion of the resources when they are queuing in the community,so that a portion of the extra cost will be generated,aiming at this problem，study how to set up the optimal service number,so that the extra cost of this part is minimum.Give the definition of Web service community,and the problem of queuing in the service community is mapped into the problem of queuing theory,the queuing model isM/M/n.Calculate the queue length of users in steady state,and get the number of queuing users in the community.The cost function is determined by the cost factor in the Web service community.The optimal service number is obtained by the marginal analysis method in economics.Experiments show that the method can effectively find the optimal number of services,and the efficiency of the method is relatively high.

Web service； community of Web service； theory of queue； marginal analysis method

2015—11—13

国家自然科学基金资助项目(61462056，61462051，71161015，81360230)；云南省重点基金资助项目(2013FA013，2013FA032，2014FA028，2014FB133)

10.13873/J.1000—9787(2016)10—0056—04

TP 311

A

1000—9787(2016)10—0056—04

何晨翔(1989-)，男，安徽芜湖人，硕士，研究方向为服务计算、软件工程。