改进递归最小二乘RBF神经网络溶解氧预测*

袁红春， 潘金晶

(上海海洋大学 信息学院,上海 201306)



改进递归最小二乘RBF神经网络溶解氧预测*

袁红春， 潘金晶

(上海海洋大学 信息学院,上海 201306)

为提高溶解氧预测的准确性，将基于改进型递归最小二乘算法优化的径向基函数(RBF)神经网络方法应用于溶解氧预测。利用K均值聚类算法进行隐层单元中心选择；利用改进型递归最小二乘算法优化RBF神经网络隐含层到输出层的权值。仿真结果表明:该方法对溶解氧的预测具有较好的非线性拟合能力，预测精度优于RBF神经网络和递归最小二乘算法优化的RBF神经网络。

溶解氧预测; 改进型递归最小二乘算法; 径向基函数神经网络； 递归最小二乘算法

0 引 言

溶解氧易受水质，养殖密度等诸多因素影响,具有非线性，模糊不确定，多变量等特点[1]。传统的溶解氧预测方法主要包括：回归预测法[2～4],时间序列法[5,6]，水质模型预测法等。这些方法存在一些不足：回归预测法需要的样本量比较大，且预测精度不能保证；时间序列法操作简便，但缺点在于没有考虑整个水环境发展的新动向和其他因素的影响，准确性较差；而水质模型法的缺点在于所需参数多，费时费力，在实际应用中很难获得全部参数，预测效果不理想。随着计算智能与仿生技术的发展，涌现出许多基于计算智能的新型预测方法,主要包括：灰色理论法，人工神经网络法，支持向量回归机(SVR)等。灰色理论法在溶解氧数据序列不以指数规律变化时预测结果偏差较大；SVR具有坚实的理论基础,可获得全局最优解，但缺点在于SVR参数决定着模型性能，至今仍没有成熟的解决方案[7,8]。人工神经网络具有自主学习、信息记忆、知识推理、优化计算和非线性拟合能力强等特点，因而广泛用于水产养殖水质预测中[10]。

RBF人工神经网络是一种高效的前馈式神经网络，具有强大的非线性问题处理及泛化能力，广泛应用于溶解氧的预测。但RBF神经网络连接权值对神经网络的性能影响较大且收敛速度较慢，因而如何优化RBF神经网络的连接权值成为提高其逼近精度的关键。改进型递归最小二乘算法通过判断神经网络估计误差和逼近误差之间的大小关系，决定相关的连接权值的修改，提高了RBF神经网络的预测精度。

本文将改进型递归最小二乘算法与RBF神经网络相结合，对溶解氧进行预测，并通过实验验证了该模型在溶解氧预测方面的优势。

1 RBF神经网络

RBF神经网络[10]是一种性能优良的前向型神经网络，由输入层，隐含层和输出层三层组成。

RBF神经网络从输入层到隐含层的变换是非线性的，一般通过RBF来实现，如高斯函数

(1)

式中 σj为第j个感知的变量(可以自由选择的参数)，决定着该基函数围绕中心点的宽度。M是隐含层节点的个数，X=(x1,x2,…,xn)为网络的输入向量，Cj=(cj1,cj2,…,cjn)为隐含层第j个神经元的中心矢量，与X具有相同的维数。‖X-Cj‖向量X-Cj的欧几里得范数，φj(X)为隐含层第j个神经元的输出。而从隐含层到输出层的变换是线性的，网络输出为隐含层输出的加权求和，输出形式为

(2)

式中 y(k)为 输出层第k个节点的输出，L为输出节点数，φj(x)为隐含层输出,wkj为隐含层第j个神经元节点与输出层第k个神经元节点的连接权值。

2 算法原理与建模

2.1 改进型递归最小二乘算法

改进型递归最小二乘算法在RBF神经网络隐层到输出层的连接权值调整过程中不是对所有的权值参数进行修改，而是对估计误差大于或等于逼近误差项的相关神经元连接权值进行修改。改进型递归最小二乘算法具体内容如下[11]：

将RBF神经网络描述为线性回归模型形式

(3)

式中 y(t)为RBF神经网络的输出，ji(x)为第i个回归量，对应于神经网络隐含层输出Φ(x)，其值由当前输入x(t)确定，wi(t)为第i个线性参数；e(t)为其逼近误差项；K为线性参数的维数，对应于神经网络隐含层神经元数；在当前时刻t时，如果神经网络已经运行n步，将RBF神经网络描述为矩阵形式

Y(t)=J(t)θ(t)+E(t)

Y(t)= [y(1),y(2),…,y(t)]T∈Rn,

jT(i)=[j1(i),j2(i),…,jk(i)],1≤i≤n,

J(t)=[jT(1),jT(2),…,jT(t)]T∈Rn×K，

θ(t)=wT(t)=[w1(t),w2(t),…,wK(t)]T∈RK,

E(t)=[e(1),e(2),…,e(t)]T∈Rn

(4)

将回归量的参数用以下形式表示

(5)

在时刻t,定义一个K的埃尔米特矩阵Q

Q(t)=[JT(t)J(t)]-1

(6)

利用矩阵Q，学习过程如下

L(t)=Q(t)J(t)=Q(t-1)J(t)

=Q(t-1)J(t)[1+JT(t)Q(t-1)J(t)]-1

Q(t)=[I-L(t)JT(t)]Q(t-1)

(7)

为了加快学习过程的速度，将式(7)重新调整为

L(t)=Q(t)J(t)=Q(t-1)J(t)

=Q(t-1)J(t)[1+JT(t)Q(t-1)J(t)]-1

Q(t)=[I-αL(t)JT(t)]Q(t-1)

(8)

式中α=1,|ε(t)|≥|e(t)|;α=0,|ε(t)|≤|e(t)|,e(t)是逼近误差，ε(t)估计误差,即

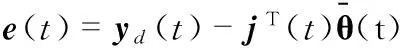
(9)

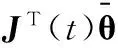
2.2 溶解氧预测相关指标选取

溶解氧是绝大部分海洋生物赖以生存的基本条件 。研究表明，温度直接影响水体中溶解氧含量，海水温度升高，动植物呼吸作用加强，有机物分解加快，消耗了较多的溶解氧 。一般来说，海水的温度越高，水体中溶解的盐分越大，水中的溶解氧越低。其次，pH也是影响水体中溶解氧含量的关键因素之一 。这种关系主要受控于水体中海洋生物的光合作用。光合作用可以表达为

C106H263O110N16P+138O2

(10)

光合作用消耗CO2和H+,使其在海水中的含量减少，导致pH升高；同时光合作用产生了大量的溶解氧，因而溶解氧含量随着pH的升高而增大。海水中的氧化还原电位也和水体中的溶解氧含量有着密切的关系，其数值与水体中溶解氧含量的对数呈线性关系，一般来说，水体中含氧量越低，氧化还原电位越低。

基于上述对海水中溶解氧相关指标的分析，本文选取近岸海域水质监测系统所监测到的水体的水温、盐度、pH以及氧化还原电位来对水体中的溶解氧含量进行预测。

2.3 数据样本与预处理

采用的水质数据为近岸海域水质监测系统2014年4月15日～4月30日的水质监测数据，该组数据由传感器采集取得。每2h取一组数据，总共202组：训练集(182×4)和测试集(20×4)，部分样本数据如表1所示。

为了精准预测溶解氧，将样本数据归一化至[-1,1]区间内

(11)

式中 xk为第k个输入样本，yk为第k个输入样本xk的归一化值，xmax,xmin分别为输入样本中的最大值及最小值，ymax,ymin的值分别为1，-1。

2.4 改进型递归最小二乘RBF神经网络溶解氧预测模型

创建三层RBF神经网络，网络的输入层是4种与溶解氧相关的水质指标值，网络输出为溶解氧(DO)，即输入层节点数为4；隐含层节点数为30，建模步骤如下：

1)当对RBF神经网络隐含层神经元数目M确定之后，从输入样本xi(i=1,2,…,n)中选择M个样本作为聚类中心；同时需要按照临近原则,如表1。

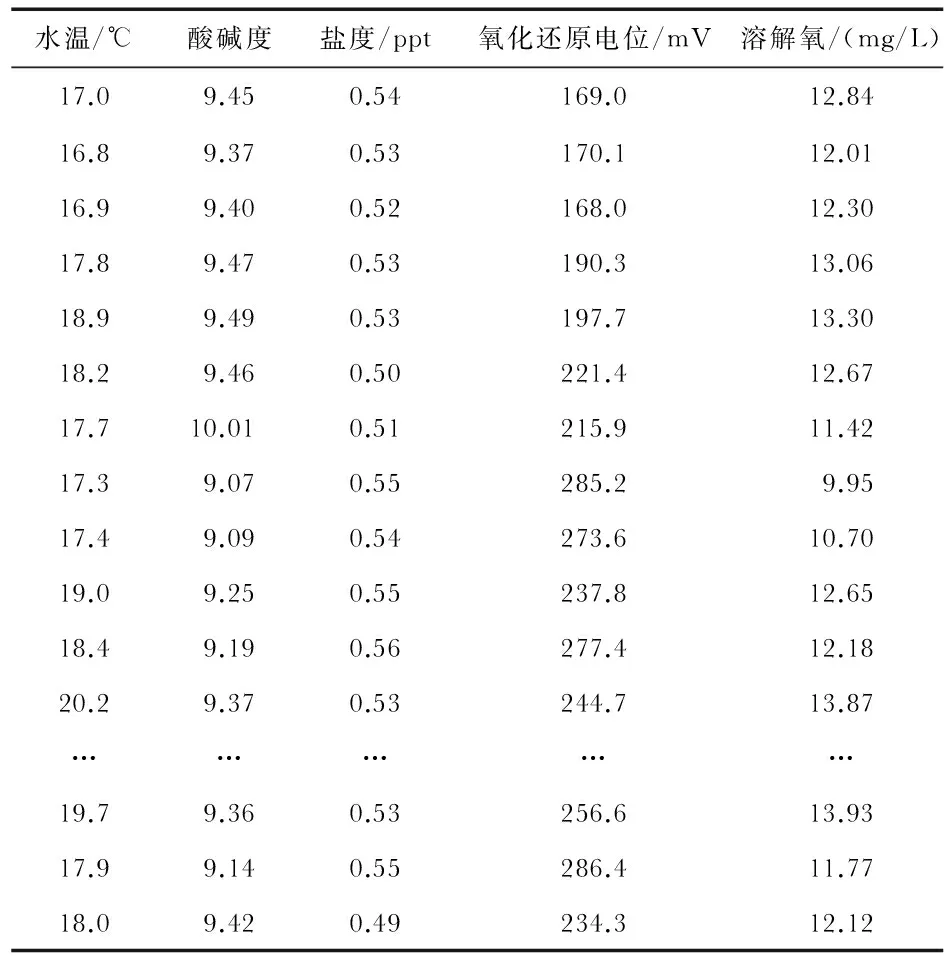
表1 样本数据

对样本数据进行分类处理。将满足dj=min|xi-Cj|(i=1,2,…,n;j=1,2,…,M)的xi分配给中心Cj(j=1,2,…,M)多输入聚类集合θj(j=1,2,…，M),即xi∈θj；先计算出聚类中心Cj(即θj中样本多平均值)，然后再具体求出θj的平均值

(12)

2)采用高斯函数作为RBF,得

(13)

采用以下公式计算σj，即

(14)

式中 dM为所选中心的最大距离。

3)RBF神经网络t时刻输出

y(k)=A(k,:)W(t)

(15)

随机产生t时刻初始权值W=rand(n,1),n为RBF神经网络隐层神经元的个数。

4)逼近误差函数为

e(k)=f(k)-y(k)

(16)

式中f(k)为期望输出值。

5)性能指标

(17)

6)计算增益向量

(18)

式中λ的选择范围一般在0.95≤λ≤0.99。当参数变化快时，λ取小点；当参数变化慢时，λ取大点。

7)计算t+1时刻神经网络权值

W(t+1)=W(t)+Q(k)e(k)

(19)

8)估计误差函数为

T(k)=f(k)-A(k,:)W(t+1)

(20)

9)比较估计误差与逼近误差的绝对值大小，如果逼近误差绝对值小于估计误差绝对值，则t+1时刻神经网络隐含层到输出层的权值不更新;否则，更新t+1时刻隐层到输出层的权值，权值更新公式为式(19)。

10)更新矩阵P(k)，即

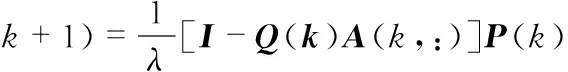
k=1,2,…,m

(21)

式中m为训练集的样本个数，设P的初始值为P(0)=αI∈Rn×n,Rn×n中n为神经网络隐含层的神经元个数。

11)对样本数据进行训练，如果样本数据没有训练完，返回步骤(1)重复上述过程；否则，如果性能指标J>Tol(Tol为期望性能指标),令J=0,返回步骤(2)对样本数据重新训练，否则结束训练，输出神经网络权值向量W，即为改进型递归最小二乘算法优化的RBF神经网络训练的隐含层到输出层的最优权值。

3 仿真结果与分析

3.1 改进型递归最小二乘RBF仿真结果

运用Matlab仿真如图1所示，改进型递归最小二乘算法优化的RBF神经网络模型得到的水溶解氧(DO)预测输出与期望输出有较好的吻合。

预测结果与隐含层节点数有关，从表2中得出，当隐含层节点数为30时，均方误差最小。

图1 改进模型预测结果Fig 1 Predicted results of improved model

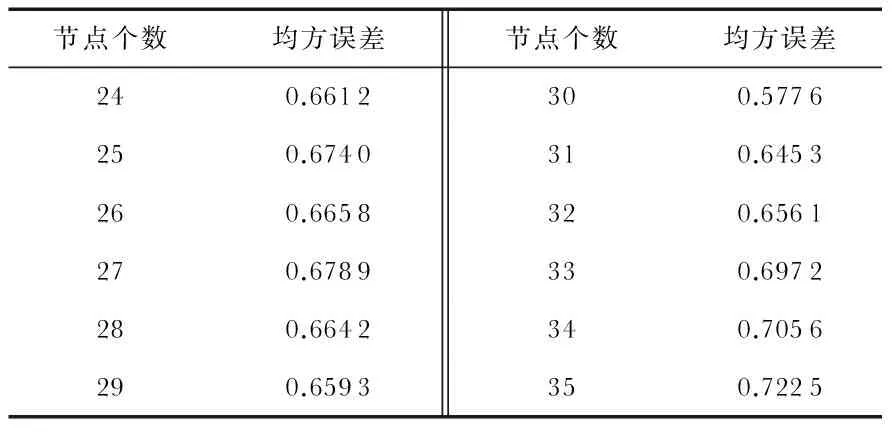
节点个数均方误差节点个数均方误差240.6612300.5776250.6740310.6453260.6658320.6561270.6789330.6972280.6642340.7056290.6593350.7225

3.2 预测算法比较

为了更好地分析改进型递归最小二乘RBF神经网络的溶解氧预测结果，用递归最小二乘算法优化的RBF与RBF神经网络也对溶解氧进行了预测。采用改进型递归最小二乘RBF，递归最小二乘RBF与RBF神经网络得到的溶解氧预测结果比较如图2和图3所示，包括两条曲线，预测曲线与误差曲线。从曲线可以看出，改进型递归最小二乘RBF神经网络的预测误差始终小于递归最小二乘RBF与RBF神经网络。从图中可以看出，改进型递归最小二乘优化的RBF神经网络预测模型的预测值更加接近溶解氧的实际值，比递归最小二乘算法优化的RBF与RBF神经网络更加准确。

图2 预测曲线Fig 2 Predicting curve

图3 误差曲线Fig 3 Error curve

4 结束语

本文以溶解氧的预测为例，针对近岸海域水质监测系统2014年4月16日～4月30日的水质监测数据，通过使用改进型递归最小二乘算法优化的RBF神经网络训练神经网络隐含层到输出层的网络连接权值，得到一种高效的人工神经网络。将获得的改进型递归最小二乘RBF神经网络模型与溶解氧预测系统结合，对RBF神经网络，递归最小二乘RBF神经网络以及改进型递归最小二乘RBF神经网络模型进行实验仿真并对预测结果进行了详细分析。结果表明：改进型递归最小二乘算法优化的RBF神经网络较之于RBF神经网络，递归最小二乘算法优化的RBF神经网络具有预测精度高，泛化能力强等性质，在溶解氧预测系统中的应用效果显著。

[1] 管崇武，刘 晃，宋红桥，等.涌浪机在对虾养殖中的增氧作用[J].农业工程学报，2012,28(9):208-212.

[2] 王 立，刘载文，吴成瑞.基于多元时序分析的水华预测及因素分析方法[J].化工学报，2013,64(12):4649-4655.

[3] 朱丽楠，官 涤，王永军，等.典型湖库富营养化的模糊综合评价研究[J].长江流域资源与环境,2012,21(9):1131-1136.

[4] 陈明千，李 艳，李克锋，等.水库降低水位运行对库区水质影响的预测研究[J].四川大学学报:工程科学版，2012,44(1):32-36.

[5] Wu J,Lu J,Wang J.Application of chaos and fractal models to water quality time series prediction[J].Environmental Modelling & Software,2009,24(5):632-636.

[6] Zou S,Yu Y.A dynamic factor model for multivariate water quality time series with trends[J].Journal of Hydrology,1996,178(1-4):381-400.

[7] Lü Jiake，Wang Xuan,Zou Wei.A hybrid approach of support vector machine with differential evolution optimization for water quality prediction[J].Journal of Convergence Information Technology,2013,8(2):1158-1163.

[8] Tan G H,Yan J Z,Gao C,et al.Prediction of water quality time series data based on least squares support vector machine[J].Procedia Engineering,2012,31:1194-1199.

[9] Xu L,Liu S.Study of short-term water quality prediction model based on wavelet neural network[J].Mathematical and Computer Modelling,2013,58(3～4):807813.

[10] Broomhaced Lowe.An efficient multiobjective learning algorithm for RBF neural network[J].Neurocomputing,1988,7(8):16-21.

[11] 乔俊飞，韩红桂.前馈神经网络分析与设计[M].北京:科学出版社,2015.

[12] 石晓勇，陆 茸，张传松，等.长江口邻近海域溶解氧分布特征及主要影响因素[J].中国海洋大学学报:自然科学版，2006,36(2):287-290.

[13] 王玉衡，蒋国昌，董恒霖.春季浙江南部海区溶解氧、pH和营养盐分布特征及相互关系研究[J].海洋学报，1990,12(5):654-660.

[14] 殷 燕，吴志旭，刘明亮，等.千岛湖溶解氧的动态分布特征及其影响因素分析[J].环境科学,2014,35(7):2539-2546.

[15] Tang Xiao，Wang Jia.Factors affecting the ORP in sea water[J].Corrosion Mechanism and Protection of Environmental Effect，2004(8):37-39.

Dissolved oxygen prediction based on improved recursive least square RBF neural network*

YUAN Hong-chun, PAN Jin-jing

(College of Information,Shanghai Ocean University,Shanghai 201306,China)

In order to improve accuracy of dissolved oxygen prediction,radial basis function(RBF)neural network based on improved recursive least square algorithm is applied to predict the dissolved oxygen.Using K means clustering algorithm to choose the center of hidden layer units and improved recursive least square algorithm is used to optimize the weights of hidden layer to output layer of RBF neural network.Simulation results show that the proposed method has good nonlinear fitting ability and its prediction precision is higher than RBF neural network and RBF neural network based on recusive least square algorithm.

dissolved oxygen prediction; improved recursive least square algorithm; RBF neural network; recursive least squre algorithm

2015—11—05

上海市科学技术委员会技术支撑项目(14391901400)

10.13873/J.1000—9787(2016)10—0020—04

TP 389.1

A

1000—9787(2016)10—0020—04

袁红春(1971-)，男，江苏海门人，博士，教授，硕士研究生导师,主要从事专家系统、智能计算、智能信息处理等研究工作。