实时嵌入式异构环境下多优先级混合任务调度动态策略*

马 晨, 肖智斌， 张 晶， 范洪博， 车国霖

(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)



实时嵌入式异构环境下多优先级混合任务调度动态策略*

马 晨, 肖智斌， 张 晶， 范洪博， 车国霖

(昆明理工大学 信息工程与自动化学院,云南 昆明 650500)

针对现有异构环境下的调度策略，引入迫切密度和剩余价值密度，分析迫切密度和剩余价值密度调节任务执行紧急程度的影响、对优先级制定,通过构建单有向无环图(DAG)系统模型实现了混合任务的动态调度。仿真实验结果表明：该调度策略在系统负载较高的情况下,仍有较优的任务执行效能和避免颠簸现象。

迫切密度； 剩余价值密度； 有向无环图； 动态调度； 颠簸； 实时性

0 引 言

随着实时嵌入式工业控制软件的不断发展，大量异构设备接入到信息物理融合系统](cyber-physical system,CPS)中]，由此形成了一个异构并行分布式处理环境， 将用户的任务分解成若干相关子任务进行并行处理，构建实时嵌入式系统任务调度形式相互作用模型]，可以有效地提高系统处理性能，从而并行协作完成任务。异构并行分布式处理系统与同构系统相比，具有多个不同架构的计算节点，这些节点在处理能力、存储方式、访问方式等上都存在差异]。如何将实时任务分解后分配到不同节点上进行调度处理和资源分配]便成为能否充分发挥并行分布式处理性能的首要问题8〗。

目前，针对异构并行分布式处理环境多以随机搜索算法、表调度算法、任务复制法为基础。遗传调度算法和基本粒子群调度算法]是常见的随机搜索算法，但遗传算法运行时需大量参数，交叉和变异概率需大量经验数据才能确定，且由于遗传算法自身存在早熟和不收敛，性能显著降低。

表调度法中，异构动态优先级任务表调度(heteroge-neous dynamic priority task scheduling，HDPTS)算法是异构环境下任务处理时间具有非单调性的动态优先级任务调度算法，虽实现调度顺序动态改变，但无法保证任务完成的可靠性，尤其是硬实时任务\〗。

任务复制法是对多个接受消息的处理器发送任务消息副本，将外部通信转化为内部通信，减少处理器间通信时间，但由于复制大量副本，降低了处理时间。

本文针对异构并行分布式处理环境中调度算法存在的不足,12〗，根据子任务间相互依赖关系构造有向无环图(directed acyclic graph,DAG)，并引入迫切程度和剩余价值密度概念，提出一种针对异构并行分布式处理环境下的多优先级混合任务动态调度策略,仿真实验结果表明:该调度策略在系统负载较高的情况下仍有较优的任务执行效能和避免颠簸现象。

1 多优先级混合任务动态调度策略

1.1 系统模型

1.1.1 DAG构建

本文将一组相互依赖的子任务用DAG来表示：

定义1G=(T,e),G′=(T′,e′)。其中，G为硬实时子任务的DAG，G′为软实时子任务的DAG。

定义2Tα={(tαi,i=1,2,3，…，n),α=1,2,3…N}为N个硬实时任务，且每个任务分解为n个有序硬实时子任务的集合。

本文假定单DAG只存在一个开始任务和一个结束任务。

1.1.2 相关定义

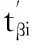
定义8 R={Rφ,φ=1,2,3，…，l}。其中，R为物联网所有处理资源的集合，l为处理资源个数，tiφ,p表示第i个子任务分配到Rφ上处于第p个位置。

因此，包含有若干相互依赖的子任务的集合可以定义如下

Tα={sTα,tαi,dLαi,DLα,δαi,ωαiφ,

ESTαiφ,p,EFTαiφ,p,LFTαiξ,p,Vαi,

VDαi,Vα,α=1,2,3,…,N}

(1)

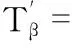
(2)

(3)

式中 Vαi×φ(1≤α≤N,1≤i≤n,1≤φ≤l)为Tα中的tαi在Rφ上的执行速率，该值可通过将子任务在相应处理资源下反复试验并经过统计计算得来。

结合式(3)和δαi，即可算出单个子任务在不同处理资源下的预估执行时间

(4)

根据公式(4)可知，在Rφ下无中断执行所需ωαiφ与δαi成正比，与vαiφ成反比。

式中ESTαiφ,p为tαi在Rφ上的最早开始时刻；ωαkλ为tαi的父任务tαk在Rλ上的预估执行时间；lagαiφ为tαk在Rλ上的等待或延时；cTαk,αi为父任务tαk与子任务tαi之间通信所花费的时间；EFTiφ,p-1为tαiφ,p在的Rφ上前一个位置上tαiφ,p-1的最早开始时刻。由于本调度方法采用抢占式策略，因此,当tαi被迫让出处理资源时，实际执行时间将延长，tαi的最早开始时间将推迟

EFTαiφ,p=ESTαiφ,p+minωαiφ

(6)

式中EFTαiφ,p为tαi在Rφ上的最早完成时刻

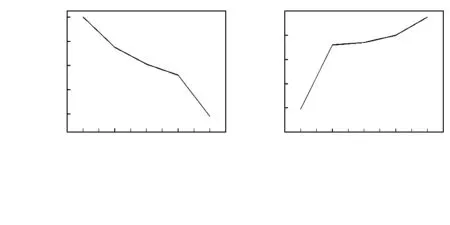
LFTαiφ,p=PESTαiφ,p+maxωαiφ,且LFTαiφ,p

(7)

式中LFTαiξ,p为tαi在Rφ上的最迟完成时刻。

ρVαi=Vαt/ωαiφ

(8)

式中Vαi为tαi的价值；ρVαi为tαi的价值密度。

价值密度ρVαi，即单位预估执行时间上的价值，与ωαiφ成反比，与Vαi成正比。

(9)

式中Vα为Tα的总价值。

1.2 多优先级分析

1.2.1 迫切密度

在本文以硬实时任务为例，引入迫切密度概念，保证任务能够在最迟完成时刻前完成，不影响子任务和后续任务执行。

证明：假设tαi在Rφ上的等待或延时时间为lagαiφ，预估执行时间为ωaiφ,设其在Rφ上最早开始时刻任务的执行迫切密度为ρEαi，且对迫切密度追加一个权重系数q，则

(10)

根据式(7)得

(11)

根据式(11)知，当比值大于1，子任务即使被分配到最快的处理资源上也可能无法在截止期内执行完成。

1.2.2 剩余价值密度

价值是实时任务系统中的内在属性，本文以硬实时任务为例，引入迫切密度概念，保证紧急任务有限执行。

定理2 价值密度等于子任务价值与预估执行时间之商，即单位预估执行时间内的价值。

证明：根据式(8)可知，价值密度为

ρVαi=Vαi/ωαiφ

若子任务已经执行的单位时间为γ，则子任务的预估动态价值(estimate dynamic value,EDV)为

(12)

式中γ为任务已执行单位时间逐渐递增且小于ωαiφ。

剩余价值密度为

(13)

定理3 当0≤γ≤ωaiφ时，对式(11)增加一个加速参数τ，τ>1且取定值，子任务的预估立即价值随γ递增。

证明：构造函数

(14)

并对式(13)求一阶导数， 即

(15)

1.3 动态抢占调度策略

异构并行分布式处理环境下调度一般包含两个问题：1)如何合理分配具有相互依赖性质的子任务到多处理资源上。2)分配在单处理资源上多个子任务顺序的排序，即任务调度\〗。

实时任务包含硬、软实时任务，软实时任务允许发生超时错误，且超时对系统影响较小；硬实时任务对时限要求较刚性，要求指定任务在规定时间内必须完成，一旦超时不仅对系统造成极其严重的影响\〗，诸如对实时任务有严格要求的产品一旦出现这种情况会造成无法想象的严重后果\〗。本文的动态调度策略为保证硬实时任务顺利完成，允许硬实时任务抢占软实时任务处理资源，在保证硬实时任务的执行可靠性下最大限度\〗的完成软实时任务。

在可抢占的动态实时任务调度中，任务的执行顺序会随着参数的改变而动态变化，当后续任务的优先级超过当前执行任务的优先级时便会发生抢占现象。随着后续任务占用处理资源，其他任务又重新开始进行优先级排序，若有多个任务的优先级交替上升从而反复抢占处理器，则称为“颠簸”现象，进行多次上下文切换，造成系统资源大量浪费。为了避免此类事件发生，合理的抢占策略是关键。本文的基本策略是：硬实时子任务可抢占软实时子任务，硬实时子任务之间可互相抢占。

依据前一节中所论述的ρEαi和ρRVαi，提出一种多优先级混合任务动态调度策略。本文所提出的调度策略以实现任务执行迫切程度和动态价值累积最优为目标。构造动态优先级函数：DPαi=m×ρEαi+n×ρRVαi，其中0≤m≤1,0≤n≤1为权重系数，且m+n=1。

由式(11)和式(13)可知

(16)

假设硬实时子任务tai被分配到处理资源cφ上，保证它能顺利执行完成的基本条件是maxωaiξ-lagaiφ>minωaiφ，随着等待时间lagaiφ的不断增加，其优先级也不断增加，若超过当前任务的优先级则会发生抢占，此时按照当前执行任务种类的不同有两种处理策略。

1.3.1 软实时任务

1.3.2 硬实时任务

设taj已执行时间为tajed,则剩余执行时间为ωaj-tajed。为了消除“颠簸”现象，此处分为两种情况：

2)被抢占过。为防止taj被频繁抢占导致执行效率不高，此时tai不进行抢占，若maxωaiφ-lagaiφ-ωajφ-tajed>minωaiφ，tai继续等待。若maxωaiφ-lagaiφ-ωajφ-tajed

2 实验仿真

2.1 仿真环境

仿真环境均为CPU为Intel(R) Core(TM) i5—4210H CPU @ 2.90 GHz 2.90 GHz，内存为8 G，64位操作系统的台式机上进行，实验平台采用Matlab实验仿真平台。试验中所涉及的时间参数都以EXCEL随机函数RAND的形式产生。

实验对本文提出的动态抢占调度策略进行基础性能分析，然后与传统的最小空闲时间优先(least slack first，LSF)调度算法，最早截止时间优先(earliest deadline first，EDF)调度算法进行对比。

2.2 仿真性能指标

实验中，采用的仿真性能指标为：任务累计价值和抢占次数。

2.3 仿真比较

2.3.1 基础性能分析

在该实验中，依据随机数产生取实验中所用参数如表1所示。

表1 实验所用参数

实验1 固定参数m=0.5,n=0.5,τ=2 ，变量参数q=0.2,0.4,0.6,0.8，分析q对调度策略基础性能的影响，实验结果如图1所示。

图1 变量参数q对调度策略基础性能的影响Fig 1 Influence of parameter q on basic performance of scheduling policy

实验2 固定参数m=0.5,n=0.5,q=0.5，变量参数τ=3,4,5,6,7，分析τ对调度策略基础性能的影响，实验结果如图2所示。

图2 变量参数τ对调度策略基础性能的影响Fig 2 Influence of parameter τ on performance of scheduling policy

实验3 固定参数τ=2,q=0.5，变量参数m=0.2,0.4,0.6,0.8,n=0.8,0.6,0.4,0.2，分析m,n对调度策略基础性能的影响。实验结果如图3所示。

图3 变量参数m,n对调度策略基础性能的影响Fig 3 Influence of parameter m,n on performance of scheduling policy

2.3.2 算法对比分析

算法对比分析将本调度策略与LSF,EDF～19〗进行对比，仿真实验在不同系统负载下，选取对比的三种调度算法，在仿真实验过程中所用参数依旧以随机数方式产生，在不考虑干扰因素情况下，仿真结果如图4。对影响仿真实验结果的干扰因素，将在以后的工作中进行研究分析。

图4 算法对比仿真实验结果Fig 4 Simulation experiment results of algorithms comparison

如图4(a),(b)所示:1)累计价值：当系统负载在1～3时，本调度策略劣于LSF，略优于EDF；当系统负载在3～7时，三种调度算法没有明显优劣程度；当系统负载愈来愈大时，本调度策略对比其他两种调度算法有明显优势。2)抢占次数：当系统负载在1～3时，本调度策明显优于LSF和EDF；当系统负载在3～7时，三种调度算法没有明显优劣程度；当系统负载愈来愈大时，本调度策略对比其他两种调度算法有明显优势。

综上所述，本调度策略在系统负载不断增大过程中，无论是累计价值，或抢占次数都明显优于其他两种算法。

3 结束语

本文通过比较传统的调度算法,21〗，分析了当前异构环境下调度算法存在的不足，根据分解后的硬实时和软实时任务的子任务之间的相互依赖关系构造有向无环图，建立单DAG异构系统模型，并明确模型内相关定义，通过引入ρEαi和ρRVαi概念，并对其做详细定义与相关证明，基于多优先级任务构造迫切密度和剩余价值密度优先级队列，提出了一种异构环境下多优先级混合任务动态调度策略，即保证了多优先级任务调度的实时性，使得混合任务得到高效处理，同时也避免了调度策略在抢占过程中的颠簸现象。最后利用不考虑干扰因素情况下的仿真实验，通过与相关传统算法进行比较，得出本调度策略在异构环境下，不仅提高了CPS实时嵌入式异构环境下调度策略的执行效能\〗，同时能够在高系统负载下较优地对混合任务进行调度，进而保证实时嵌入式工业控制系统交互行为的存在性和唯一性，更准确地表达系统资源分配与实时任务调度的确定性。

[1] 刘纯尧.信息物理融合系统的调度算法研究[D].上海：华东师范大学,2015.

[2] Bastoni A,Brandedburg B B,Anderson J H.An empirical compa-rison of global,partitioned,and clustered multiprocessor EDF schedulers]∥Proceedings of the 31st IEEE Real-Time System Symposium,San Diego,USA,2010:14-24.

[3] Jensen E D,Locke C D,Toduda H,A time-driven scheduling model for real-time operating systems]∥Proceedings of the IEEE Real-Time Systems Symposium,San Diego,CA,USA,1985:112-122.

[4] 朱怡安，黄姝娟，段俊花，等.新的混合关键任务调度算法的研究[J].电子科技大学学报,2014(2):268-271，286.

[5] 辛 宇，杨 静，谢志强.面向分布式环境的信号驱动任务调度算法[J].通信学报,2015(7):60-70.

[6] 孙 健，张兴军，董小社.异构平台实时任务的可用性提升容错调度算法[J].计算机研究与发展,2015(12):2669-2683.

[7] 孙力娟，魏 静，郭 剑，等.面向异构无线传感器网络的节点调度算法[J].电子学报,2014 (10):1907-1912.

[8] 彭 浩，韩江洪，陆 阳，等.多处理器硬实时系统的抢占阈值调度研究[J].计算机研究与发展,2015(5):1177-1186.

[9] 刘纯尧，张立臣.信息物理融合系统的动态多优先级调度[J].计算机科学,2015(1):28-32.[10] Qi X,Zhu D K,Aydin H.Cluster scheduling for real-time systems:Utilization bounds and run-time overhead[J].Journal of Real-Time Systems,2011,47(3):253-284.

[11] 曾增日.无线传感网络节点调度算法研究[D].长沙： 湖南大学,2015.

[12] 罗惠星.基于批量作业调度的算法研究[D].上海：上海师范大学,2015.

[13] 张银香.协作通信技术中的调度算法研究[D].北京：北京邮电大学,2015.

[14] 任健康.信息物理系统高效数据传输和调度机制研究[D].大连：大连理工大学,2015.

[15] 张忆文，郭锐锋.实时系统混合任务低功耗调度算法[J].吉林大学学报:工学版,2015(1):261-266.

[16] 王希杰.基于物联网技术的生态环境监测应用研究[J].传感器与微系统,2011,30(7)：149-152.

[17] 骆 坚，席 望，谢 鲲.基于异构比特速率的无线传感器网络拥塞控制技术[J].传感器与微系统,2015,34(11):23-26.

[18] Baruah S.Partitioned EDF scheduling:A closer look[J].Journal of Real-Time Systems,2013,49(6):715-729.

[19] 桑 磊，陆 阳，俞 磊.基于贪心策略的EDF调度算法优化[J].计算机工程,2015(12):96-100.

[20] 胡显俊，陈建新，周生强，等.IEEE 802．15．4实时通信调度算法研究[J].计算机科学,2015(B11):222-226,241.

[21] 田新越，李翔宇.无线传感器网络节点任务调度与功耗管理算法研究[J].传感器与微系统,2016,35(2):9-12.

Dynamic scheduling strategy for multi priority hybrid tasks in heterogeneous environment of real-time embedded systems*

MA Chen, XIAO Zhi-bin, ZHANG Jing, FAN Hong-bo, CHE Guo-lin

(Faculty of Information Engineering and Automation,Kunming University of Science and Technology,Kunming 650500,China)

Introduce concept of urgency density and surplus value density,analyze influence of urgency density and surplus value density on priority setting,adjusted the task execution degree of emergency based on weight coefficient and acceleration factor,and dynamic scheduling of hybrid task is achieved based on constructing single directed acyclic graph(DAG) system model.Simulation results show that the proposed scheduling strategy can achieve better task execution efficiency and avoid thrashing even at higher load level.

urgency density; surplus value density:directed acyclic graph(DAG); dynamic scheduling; thrash; real-time

2016—06—06

云南省应用基础研究计划重点项目(2014FA029)

10.13873/J.1000—9787(2016)10—0012—05

TP 18

A

1000—9787(2016)10—0012—05

马 晨(1989-)，男，辽宁沈阳人，硕士研究生，主要研究方向为实时与嵌入式软件、信息物理融合系统。