基于安时积分和粒子滤波修正的锂电池SOC估计*

张宏伟， 李建成， 张兵兵

(国防科学技术大学 电子科学与工程学院，湖南 长沙 410073)



基于安时积分和粒子滤波修正的锂电池SOC估计*

张宏伟， 李建成， 张兵兵

(国防科学技术大学 电子科学与工程学院，湖南 长沙 410073)

针对安时积分(AH)法的累积误差问题和卡尔曼滤波算法对系统噪声的限制，提出了粒子滤波(PF)修正安时积分误差的方案，并基于钴酸锂电池测试数据和电池等效电路模型，对算法进行仿真验证。通过与传统的AH和卡尔曼滤波法对比得出：基于AH和PF修正的方法荷电状态(SOC)估计效果较好，平均误差与标准误差均控制在2 %以内。

锂离子电池； 等效电路模型； 荷电状态； 粒子滤波; 安时积分

0 引 言

锂离子电池能量密度高，循环寿命长，电压平台高，绿色环保,锂电池的这些优势使其得到广泛的开发和应用[1]。因此，本文以锂电池的一种钴酸锂电池为研究对象。

由于电池内部复杂的电化学反应，电池荷电状态(state of charge,SOC)估计是一个非线性问题。针对非线性状态估计问题，在卡尔曼滤波的基础上，提出了扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波等等[2,3]，扩展卡尔曼算法在处理非线性问题时，使用一阶泰勒展开，因而引入了额外的误差，甚至导致滤波发散；其次，这些算法均要求观测噪声和过程噪声假设为高斯白噪声，这与实际情况不符，在实际应用中存在缺陷。粒子滤波(PF)不需要将系统噪声和观测噪声假设为高斯分布，在非线性非高斯模型中应用具有明显的优势，在处理非线性非高斯问题中显示了优越的性能，并在目标跟踪、导航定位、故障诊断、系统辨识、参数估计等领域得到广泛应用[4～6]。

本文首先介绍了PF的基本原理和实现步骤，然后在等效电路模型的基础上，建立了基于安时积分(AH)和PF修正的SOC估计方法，并通过电池测试数据对算法进行了验证。

1 PF算法

PF是一种基于蒙特卡罗仿真和序贯重要性采样的非线性滤波方法[7]。

PF算法就是基于贝叶斯估计和蒙特卡洛方法的近似数值解方法。PF算法的本质就是将整个状态空间的积分运算变为有限样本点的求和运算。标准PF在序贯重要性采样算法基础上增加了重采样算法，具体实现步骤如下：

1)初始化(k=0)

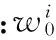
2)重要性采样

(1)

归一化权值

(2)

3)判断是否重采样

计算有效粒子数Neff，如果Neff

(3)

4)重采样

5)输出

(4)

在完成上述步骤之后，当下一时刻的测量值到来时，返回到步骤(2)，否则,结束。

2 基于AH和PF修正的SOC算法实现

2.1 PF算法的引入

根据上文关于PF理论的分析针对PF中两个关键问题：重要概率密度函数选取和重采样技术，在基本PF算法基础上进行改进。首先将高斯滤波和PF相结合，引入高斯PF，该滤波算法由Jayesh和Petar提出[8]。这种滤波算法用高斯分布近似重要密度函数产生PF的重要性分布，重要密度函数中包含新的观测信息，使得重要性概率分布更接近后验概率分布，避免了退化问题。采用高斯分布近似重要性分布使收敛性得到保证。由高斯重要密度函数得到的样本权值计算公式为

(5)

(6)

UL(k)=Uoc(SOC(k))+U1(k)+U2(k)+R0I(k)

(7)

式中 Ts为数据采样周期，CN为电池最大可用容量。

在选取好重要密度函数后，基于裂变自举PF思想[9]，采用裂变繁殖粒子的方法代替重采样。具体做法是：从k-1时刻得到的滤波结果，选用以该值为均值的一种均匀分布中采样生成新的粒子，然后用上述高斯分布近似重要密度函数产生PF的重要性分布，后验估计完成后对再生粒子的权值进行重新分配。这样既可覆盖权值小的粒子，也可以增加新的粒子，该方法避免了样本枯竭问题。

图1 电池等效电路模型Fig 1 Equivalent circuit model for battery

根据上述PF理论分析，结合本文建立的如图1所示的二阶电池等效电路模型及对应的系统方程式，制定了适合于SOC估计的改进PF方案，其基本步骤如下：

1)设置算法的初始参数，如粒子数N，高斯分布方差Q，PF修正算法开始结束的判别条件等；

5)输出SOC估计结果

(8)

6)判断是否达到修正结束条件，如果满足，则算法结束，否则,k=k+1，返回步骤(3)。

2.2 本文SOC估计与修正算法流程

在目前的SOC估计算法研究中，AH是产品化电池管理系统(batterymanagementsystem,BMS)中最常用的方法，AH计算简单、工程实现容易，但AH无反馈修正功能，由于BMS硬件数据采集精度限制，随着时间的累积，会出现较大的误差。虽然在工程应用中，在AH基础上，增加了开路电压法对初值进行修正，但当电池连续在线工作较长时间，误差得不到及时修正，SOC估计精度将大大下降。故本文SOC估计仍以AH为基础，再结合PF法进行SOC修正。

AH离散化后的计算式为

(9)

式中 SOCk-1和SOCk分别为上一时刻和当前时刻SOC对应的值，I(k)为当前时刻采集的电流值，CN为电池额定容量，Ts为数据采样周期，本文所有数据采样周期为1s。

本文SOC估计算法基本步骤如下：

1) 在电池开始工作前，首先通过开路电压法确定SOC初值。BMS采集电池搁置状态的开路电压值，通过开路电压得到此时对应的SOC值作为初值。

2)电池进入工作状态，BMS采集电池电流、端电压数据，通过式(9)AH估计SOC。

3)判断是否达到PF修正开始条件，达到则执行步骤(4)；否则，执行步骤(2)。

4)按照本文提出的PF算法步骤对SOC进行修正，并判断是否达到修正结束条件，达到则返回步骤(2)恢复AH估计SOC；否则，执行循环步骤(4)直至达到结束条件。

2.3 SOC估计结果分析

本文在对SOC估计算法进行验证时，针对电池实际使用过程中工况的不确定性，选取了不同工况的充放电电流进行电池测试和仿真验证。电池在实际应用中，电流、电压数据由BMS电路板元器件采集，电压采集芯片精度较高，但电流采集依靠霍尔传感器，测量精度一般只有1 %，传感器在使用过程中还会存在漂移电流[10]。为模拟BMS在电流数据采集过程中的噪声干扰，验证所提算法的可靠性，在标准的电流工况仿真数据中加入了干扰噪声。该电流噪声由均值分别为0，30mA的高斯噪声叠加而成，模拟实际电路中多种器件的叠加噪声及电流传感器的漂移电流。

1)脉冲放电工况算法验证

将电池脉冲放电工况测试数据载入到Matlab仿真程序中进行算法验证，算法仿真验证中，引入目前较常用的AH和EKF法，与本文提出的AH与PF修正相结合的算法(AH+PF)对比，SOC估计结果如图2，相应的估计误差如图3所示。其中，SOC实际值由电池测试系统获得。

图2 脉冲放电工况不同算法SOC估计结果Fig 2 Results of SOC estimation for pulse discharge condition

图3 脉冲放电工况不同算法SOC估计误差结果Fig 3 Results of SOC estimation error for pulse discharge condition

仿真结果表明：单独使用AH时，由于误差的累积得不到修正，SOC估计误差随着时间推移越来越大；EKF算法的闭环反馈修正效果使得SOC估计精度相对AH有了明显提高；三种算法SOC估计结果中，基于AH和PF修正的算法估计效果最好。

2)设备启动工况算法验证

为验证算法在不同工况下的适用性和复杂工况下的鲁棒性，选取设备启动(device start,DST)电流工况对算法进一步仿真验证。

不同算法的SOC估计及误差结果分别如图4、图5所示。从仿真结果可见，DST工况下，本文所提出的基于AH和PF修正的算法相比其他两种算法，仍具有较好的估算精度。表1统计出了两种工况下，不同SOC估计算法误差对比结果，可以看出AH估计误差最大达18 %，平均误差5 %以上，卡尔曼算法最大误差5 %，平均误差2 %以上。而基于AH和PF修正算法的最大误差、平均误差、标准差三项指标都优于上述两种算法，平均误差及标准差均控制在2 %以内，以上仿真对比验证了本文所提出的基于AH和PF修正算法估计SOC的可行性。

图4 DST工况不同算法SOC估计结果Fig 4 Results of SOC estimation for DST condition of different algorithms

图5 DST工况不同算法SOC估计误差结果Fig 5 Results of SOC estimation error for DST condition of different agorithms

3 结 论

本文结合AH和PF两种算法的优点，提出了基于AH和PF修正的锂电池SOC估计方法，通过与传统的AH和卡尔曼滤波法对比，在不同工况下，本文所提算法均具有较好的性能。本文钴酸锂电池试验数据均为实验室条件下测试所得，在实际工程中应用效果将是下一步重点研究内容。

表1 不同算法SOC估计误差统计

[1] 郭炳焜，王先友.锂离子电池[M].长沙：中南大学出版社，2002.

[2] Plett G.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 1:Background[J].J Power Sour,2004,134(2):252-261.

[3] Plett G.Extended Kalman filtering for battery management systems of LiPB-based HEV battery packs—Part 2:Modeling and identification[J].J Power Sources,2004,134(2):262-276.

[4] 程水英，张剑云.粒子滤波评述[J].宇航学报，2008，29(4):1099-1109.

[5] 杨小军，潘 泉.粒子滤波进展与展望[J].控制理论与应用，2006，23(2):261-265.

[6] 胡士强.敬忠良.粒子滤波算法综述[J].控制与决策,2005,20(4):361-365.

[7] 朱志宇.粒子滤波算法及其应用[M].北京：科学出版社，2010.

[8] Jayesh K H.Gaussian particle filtering[C]∥IEEE Tran-sactions on Signal Processing,2003，51(10)：2592-2601.

[9] 程水英，张剑云.裂变自举粒子滤波[J].电子学报,2008,36(3):500-504.

[10] 周越文，邓 俊，文 莹,等.基于霍尔电流传感器的电源监控系统设计[J].传感器与微系统，2015，34(10):54-56.

SOC estimation of lithium-ion battery based on algorithm of AH with PF correction*

ZHANG Hong-wei， LI Jian-cheng， ZHANG Bing-bing

(School of Electronic Science and Engineering，National University of Defense Technology，Changsha 410073，China)

Aiming at problems of accumulate-errors of Ampere-hour integral(AH) method and limitation of Kalman filtering algorithm on noise, a scheme of correction accumulate-errors of AH with particle filtering(PF) is given.Based on LCO battery testing data and model for battery equivalent circuit,the algorithm is verified by using simulation.Compared with AH method and Kalman filtering algorithm,the algorithm of AH with PF correction is better on estimation of state of charge(SOC),average error and standard error are both less than 2 %.

lithium-ion battery; equivalent circuit model; state of charge(SOC); particle filtering(PF); Ampere-hour integral(AH)

2015—11—30

国家自然科学基金资助项目(61303265)

10.13873/J.1000—9787(2016)10—0004—04

TP 212.3

A

1000—9787(2016)10—0004—04

张宏伟(1989-)，男，山西汾阳人，硕士研究生，主要研究方向为新能源应用技术。

研究与探讨