四鞍座设备的强度校核
郝兰
压力容器
四鞍座设备的强度校核
郝兰*
(南京天华化学工程有限公司)
将卧式容器的多鞍座问题转化为多个双鞍座卧式容器来计算。利用三弯矩方程,分别计算各鞍座处的弯矩、支承力和极值弯矩,找出最大弯矩和鞍座反力。按NB/T 47042—2014《卧式容器》中的公式和方法进行应力计算及校核,得到强度校核结果。
四鞍座弯矩应力计算强度校核卧式容器
长期以来,由于多鞍座卧式容器在设计和使用上存在一些问题,例如设计方法不可靠、鞍座沉降不均匀等问题,因此设计者在工业应用中都尽量避免采用多鞍座。但有些场合设备的尺寸较长,必须采用多鞍座支撑。例如:天然气净化装置中,钢制硫回收冷凝器;铁路枕木防腐行业用于浸注枕木的蒸制罐;炼油厂环保用废气排放烟囱等。这些设备均可视为超长的多支撑卧式容器。
1 四鞍座卧式容器设计计算方法简介
四鞍座卧式容器相对于双鞍座来说,中间增加了2个多余约束,静不定次数为二。假想在每个鞍座的上方,将容器切开并装上铰链,这就相当于把这些截面上的弯矩作为多余约束力,它满足三弯矩方程[1-2]。这样较长容器的多鞍座问题,就可化解为多个我们熟悉的双鞍座卧式容器问题来计算。
四鞍座卧式容器设计计算的思路如下:
(1)通过连续梁及三弯矩方程计算各鞍座处的弯矩;(2)结合各鞍座处的弯矩,计算各鞍座处的支承力;(3)根据剪力图与弯矩图的性质,计算容器上的极值弯矩;(4)通过上述计算找出最大弯矩和鞍座反力,并按NB/T 47042—2014《卧式容器》[3]中的公式及方法进行应力计算和校核。
2 四鞍座卧式容器的结构及参数
本文讨论的四鞍座卧式容器的结构如图1所示。该设备的有关参数如下所述。
封头(两只):3184.6kg(含直边段),δ=16mm;
筒体(9m):质量7667.5kg,名义厚度10mm;
鞍座(4只):质量1037×4=4148kg;

图1 四鞍座卧式容器
泵(2台):质量8000kg;
设备内介质(充装系数设为1):液体质量为147008.52+20160=167168.52kg;
筒径Di为3400mm,容器内压力为常压。
3 相关力学模型简述[2]
所讨论的四鞍座卧式容器的鞍座位置如图2所示。鞍座处的受力情况、剪力图和弯矩图如图3~图5所示。图中各符号的意义如下:
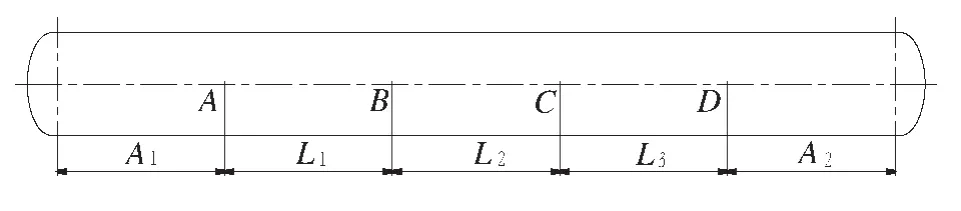
图2 鞍座位置

图3 受力情况
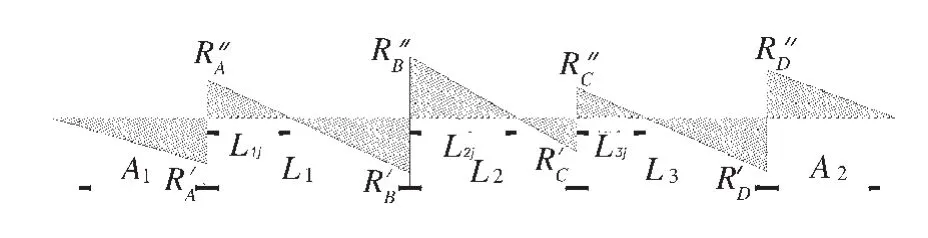
图4 剪力图
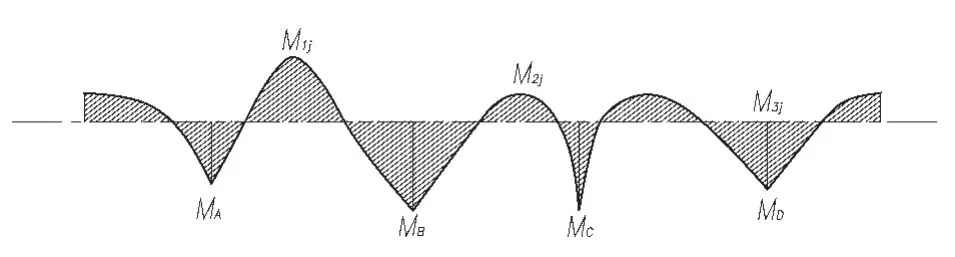
图5 弯矩图
A1——左边鞍座中心线至左封头切线的距离,为825 mm;
A2——右边鞍座中心线至右封头切线的距离,为825 mm;
hi——封头深度,为850 mm;
L1、L2、L3——鞍座AB间、BC间、CD间距离,为2450 mm;
L1j、L2j、L3j——鞍座AB间、BC间、CD间极值弯矩位置;
MA、MB、MC、MD——A、B、C、D鞍座处的弯矩;
M1j、M2j、M3j——AB间、BC间、CD间极值弯矩;
RA、RB、RC、RD——A、B、C、D鞍座处的支反力;
Ri——圆筒内半径,为1700 mm;
q——单位长度均布载荷;
设备总质量(含附件和充装介质)=190 168.6 kg;

4 计算过程[1]
目前多鞍座卧式容器的设计并没有统一的标准。本文采用三弯矩理论计算弯矩和鞍座支反力,并采用双鞍座卧式容器校核方法进行应力校核。
4.1鞍座处弯矩的计算

已知鞍座对称布置,即MB=MC。经计算:

4.2鞍座支反力的计算


所以,RA′=RD″,RA″=RD′,RB′=RC″,RB″=RC′。
考虑到支座不平、地基沉陷等因素,取1.2倍力作为鞍座设计力(参照HG 20582—2011《钢制化工容器强度计算规定》)[5],即:

同理RB=1.2(RB′+RB″)=RC=520 467.6 N
4.3各简支梁中间最大弯矩的计算
参见剪力图和弯矩图,即图4、图5。

根据剪力图和弯矩图,截面剪力为0的截面其弯矩为极值,即有
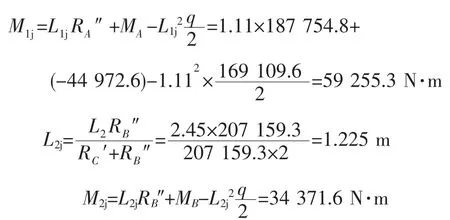
4.4应力计算和校核
4.4.1圆筒轴向应力计算和校核
4.4.1.1鞍座之间极值弯矩处圆筒截面上轴向应力
根据NB/T 47042—2014中的式(5)、式(6),可求得相邻鞍座之间极值弯矩处圆筒横截面上由压力及轴向弯矩引起的轴向应力。
鞍座A和B之间极值弯矩(M1j)处,圆筒横截面最高点处轴向应力为:

鞍座B和C之间极值弯矩(M2j)处,圆筒横截面最高点处轴向应力为:
σ1=16 174 940 N/m2
同理,鞍座A和B之间极值弯矩(M1j)处和鞍座B和C之间极值弯矩(M2j)处,圆筒横截面最低点处轴向应力分别为:
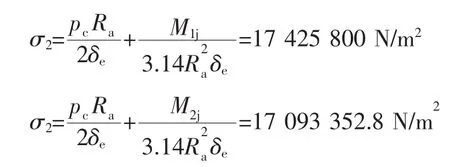
因此,鞍座A、B间极值弯矩(M1j)处横截面上:

鞍座B、C间极值弯矩(M2j)处横截面上:

由于对称性,鞍座C、D间极值弯矩(M3j)处横截面上的轴向应力与鞍座A、B间的情况相同。
式中pc——计算压力(含液柱静压力),为0.16MPa;
Ra——圆筒平均半径,Ra=Ri+δn/2=1705 mm;
δe——圆筒有效厚度,为8.2 mm;
M1——鞍座间极值弯矩;
δn——圆筒名义厚度,为10 mm。
4.4.1.2鞍座平面上由压力及轴向弯矩引起的轴向应力
鞍座平面上,由压力及轴向弯矩引起的轴向应力按文献[1]第86页式(7)、式(8)确定。
鞍座A处,圆筒横截面最高点或靠近水平中心线处(具体位置取决于鞍座处筒体是否有加强圈或被封头加强)的轴向应力:
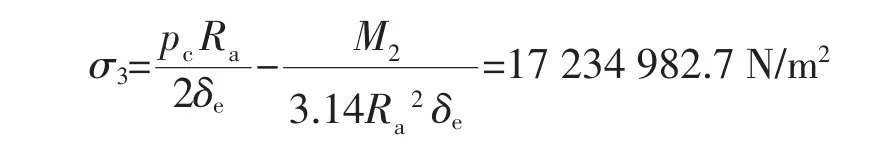
鞍座A处,圆筒横截面最低点的轴向应力:

式中M2——鞍座上的弯矩。
由NB/T 47042—2014中的表2知,当A≤Ra/2,或在鞍座平面上有加强圈加强圆筒时,取K1=1.0。
这样,经计算鞍座A处圆筒横截面上:?

同理,鞍座B处圆筒横截面上:
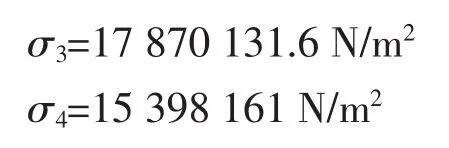
由于对称性,鞍座C处同鞍座B处,鞍座A处同鞍座D处。
4.4.1.3圆筒轴向应力的校核
根据文献[1]表3中圆筒轴向应力的校核条件,分下述两种情况。
(1)操作工况
对于操作工况,筒体内为常压,其最大应力取以上最大正值(拉应力),即在鞍座B和C平面上:
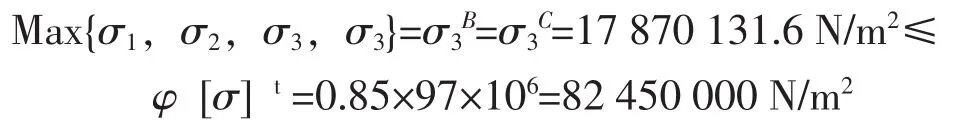
应力校核合格。其中,φ为圆筒的焊接接头系数;[σ]t为设计温度下壳体材料的许用应力。
(2)水压试验工况
对于水压试验工况(充满水),加压状态应满足以下条件,取以上最大正值(拉应力),即在鞍座B和C平面:

其中,Rel(Rp0.2)为圆筒材料在试验温度下的屈服强度或0.2%规定非比例延伸强度;数据177×106Pa为查《金属材料》[4]上册第一卷第202页表12获取。校核结论为符合要求。
4.4.2圆筒鞍座处横截面上有加强圈时筒体切向剪
应力计算和封头应力计算校核[3]
(1)边支座处横截面上
因A1=A2=825 mm<Ra/2=852.5 mm(其中Ra为圆筒的平均半径),根据文献[3]第7.3.1.2条,判定圆筒被封头加强。因此其最大剪应力根据文献[3]公式(10)计算:

封头的最大剪应力:

式中F——最大支反力,即RA、RD的最大值;
δe——圆筒有效厚度,为8.2 mm;
δhe——封头的有效厚度,按名义厚度δ=16mm计,δhe=14.2mm;
K4——当包角为150°时,取0.295。
(2)中间支座处横截面上

其中,F取RB′、RB″、RC′、RC″中最大值的1.2倍。
(3)切向剪应力校核
圆筒的切向剪应力校核:
τmax=11584452.7N/m2≤0.8[σ]t=77.6×106Pa应力校核合格。
封头的切向剪应力校核:
τhmax=6186319.7N/m2≤1.25[σ]t-σh=102.1×106Pa应力校核合格。
式中[σ]t——设计温度下容器壳体材料的许用应
力,为97 MPa;
σh——由内压在封头上引起的应力。
4.4.3圆筒周向应力计算和校核
依据文献[3]第83页,圆筒的有效宽度

式中b——支座的轴向宽度,为筋板长边与腹板
厚度之和,即b=b3+δ2=452 mm;
b3——计算圆筒与加强圈形成组合截面时,圆筒的有效宽度,mm;

δn——圆筒的名义厚度,为10 mm。
(1)加强圈在鞍座平面上的情况
“加强圈位于鞍座平面内”是指加强圈位于“鞍座平面内”两侧各小于或等于b2/2的范围内。
当加强圈位于鞍座A或D平面两侧各≤b2/2= 328 mm时,鞍座边角处圆筒的周向应力为[3]:

鞍座边角处加强圈内外缘表面的周向应力[3]:
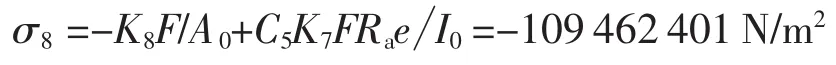
(2)加强圈靠近鞍座的情况
“加强圈靠近鞍座平面内”是指加强圈位于“鞍座平面内”两侧各大于b2/2且小于Ra/2的范围内。
加强圈位于“鞍座A或D平面内”两侧各大于b2/2=328 mm且小于Ra/2=852.5 mm的范围内,鞍座边角处圆筒的周向应力[3]:
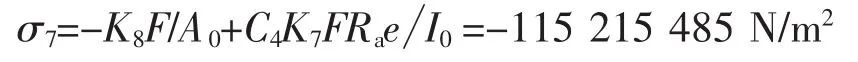
鞍座边角处加强圈内外缘表面的周向应力[3]:
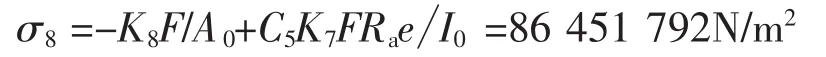
式中A0——一个支座的所有加强圈与圆筒起加强作用有效段的组合截面积之和,mm2;
I0——一个支座的所有加强圈与圆筒起加强作用有效段的组合截面对该截面形心轴X-X的惯性矩之和,见图6。
根据文献[3]相关计算方法,找出支座的所有加强圈(垫板及环筋)与圆筒三个截面(见图6阴影部分)各自的形心与面积如下:
①筒体:A1=2.14×10-3m2,y1=0.005 m;

图6 加强圈与鞍座
计算得yc=23.1 mm。
三个截面对形心轴的惯性矩为:
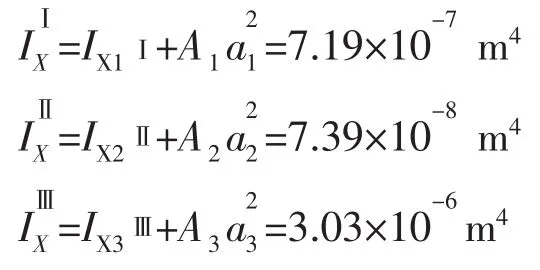
因此有

以上情况(1)、(2)分别为加强圈位于鞍座平面上或靠近鞍座两种情况下的受力状况。此时,取组合截面形心距圆筒内表面距离e为23.1 mm;Ra=1.705 m;F为1.2;A0=4.14×10-3m2;I0=3.823× 10-6m4。第1种情况加强圈在鞍座平面上,取C4= +1,C5=-1,K7=0.032,K8=0.302;第2种情况加强圈靠近鞍座,取C4=-1,C5=+1,K7=0.036,K8= 0.219。校核公式为σ7≤1.25[σ]t,σ8≤1.25[σ]tr,其中[σ]t与[σ]tr分别为设计温度下容器壳体材料与加强圈材料的许用应力,材料均为06Cr19Ni10,即[σ]t=[σ]tr=97 MPa。代入公式验证:

可见均满足周向应力强度要求。加强圈位置可灵活放置于鞍座附近。
4.4.4鞍座设计(见NB/T 47042—2014)
取b=452 mm,则腹板的水平分力为
Fs=K9F=0.259×271 876=70 416 N
查文献[3]表8,得鞍座包角为150°时,K9= 0.259。F为各鞍座的反力,为271 876 N。水平方向平均拉应力为

式中Hs——计算高度,取鞍座垫板底面至底板底
面距离和Ra/3两者中较小值,250 mm;b0——鞍座腹板厚度,22 mm;
br——鞍座垫板有效宽度,取br=b2,656 mm;δre——鞍座垫板有效厚度,14 mm。
σ9=4 795 423.6 Pa<(2/3)[σ]sa=80 000 000 Pa校核符合要求。
其中,查文献[1]表1,在-10℃≤t≤100℃时,[σ]sa=160 MPa;在100℃≤t≤200℃时,[σ]sa= 120 MPa;此处取苛刻条件,即取[σ]sa=120 MPa。
5 结论
(1)针对当前卧式容器日益大型化的趋势,四鞍座的设计从强度和结构上的可行性均得到理论的验证。
(2)设计原则一般为设一个固定支座和三个滑动支座。
(3)由于在固定支座上设置地脚螺栓,其应力通常超出许用值,因此采用固定支座与基础焊接的方法来满足要求。
[1]刘鸿文.材料力学[M].第4版.北京:高等教育出版社,1999:138-165.
[2]成大先.机械设计手册:第1卷[M].第5版.北京:化学工业出版社,2007:1-101,1-147.
[3]NB/T 47042—2014卧式容器[S].
[4]化工设备标准手册(第一卷):金属材料(上)[M].北京:化学工业部设备设计技术中心站,1996.
[5]HG/T 20582—2011钢制化工容器强度计算规定[S].
Four Saddle Equipment Strength Test
Hao Lan
By transferring the calculation model of horizontal multi-saddle vessel into multiple double-saddle vessel,the bending moment,bearing force and maximum bending moment of each saddle point were calculated separately through three moment equation.As a result,the maximum moment and support pressure could be obtained.According to the formulas and methods of horizontal vessel NB/T 47042—2014,the stress was calculated and checked,then the strength of the test results were obtained.
Four saddles;Bending moment;Stress calculation;Strength check;Horizontal vessel
TQ 050.2
10.16759/j.cnki.issn.1007-7251.2016.10.008
2015-10-01)
*郝兰,女,1977年生,高级工程师。南京市,211178。

