跨声速多级压气机中的非定常流场频域分析

赵军， 刘宝杰

1.中国民航飞行学院 航空工程学院， 广汉　618307 2.北京航空航天大学 能源与动力工程学院， 北京　100083



跨声速多级压气机中的非定常流场频域分析

赵军1， 刘宝杰2,*

1.中国民航飞行学院 航空工程学院， 广汉618307 2.北京航空航天大学 能源与动力工程学院， 北京100083

基于三维定常Denton程序发展了三维非定常计算程序，对三维跨声速多级压气机近失速点进行了定常与非定常数值模拟，并在此基础上对典型径向截面的非定常流场进行了频域分析。结果表明：通过对非定常频域图谱的研究，从一个全新的视角来分析非定常流场，可以看到一些在时域流场中很难直观看到的现象；轴向速度受尾迹的影响非常大，且在沿流向发展过程中，随着谐波阶次增加，幅值沿轴向的振荡幅度降低，幅值衰减的速度也加快；各叶排进口1阶谐波幅值在S3面内的分布受到下游叶排的势干扰，周向最大值点沿径向的走势与叶型的径向弯曲一致；气流密度、静压和总压受尾迹的影响较小，而气流静温、总温受尾迹的影响较大。

航空发动机； 跨声速； 压气机； 非定常计算； 频域分析

旋转叶轮机械内部的流动是非定常的。当前叶轮机械数值模拟普遍采用的有定常模拟技术和非定常模拟技术。前者在多叶排交界面处理时采用掺混面平均的方式忽略了上下游的非定常相互作用，而后者虽完整保留非定常细节却因计算量庞大而难以应用于工程设计。

1998年He和Ning[1]提出了一种求解非定常的新思路——非线性谐波法，并得到了进一步的发展[2-4]。该方法将非定常流场分成时均流场和脉动流场两部分进行耦合求解[5-7]。时均流场通过解包含确定应力的时均流动方程得到，而脉动方程则通过在频域内求解N阶谐波方程得到。由此，第1次提出了在频域场进行非定常研究的概念。

将时域信号变换至频域加以分析的方法称为频谱分析。频谱分析的目的是把复杂的时间历程波形经过傅里叶变换分解为若干单一的谐波分量来研究，以获得信号的频率结构以及各频率处的幅值信息。通过变换到频率域，研究者可以从一个全新的视角观察到很多信号里面隐含但在时域中不直观的信息。

目前，关于轴流叶轮机械转子与静子之间的非定常相互干扰作用的数值研究很多，大多数都采用Jameson的双时间步法。而对于轴流转子与静子之间相互干扰产生的非定常脉动的频域分析研究较少。尤其在多级跨声速压气机中，目前除He等的工作之外，从频域的视角深入分析非定常的文献很少。王英锋等[8]针对“IGV+Rotor”(Inlit Guide Vane， IGV,进口导流叶片)的单级低速轴流压气机进行了上游叶片尾迹对转子叶片非定常表面压力频谱特性影响的研究，通过用微型压力传感器测量转子叶片不同叶高位置压力波动情况，并对测得数据做了深入的频谱分析。魏宝锋等[9]采用NUMECA软件对某单级离心压气机算例进行了双时间步非定常数值模拟，并对离心叶轮与扩压器之间的非定常扰动进行了频域分析。

文献[10]基于NUMECA软件对单级轴流压气机进行非定常计算并开展了初步的非定常压力频谱研究。本文在其基础上采用基于三维定常Denton程序发展的三维非定常计算程序对某多级轴流压气机进行了定常与非定常数值模拟，并在此基础上对若干典型径向截面的非定常流场进行了频域分析，重点研究了非定常轴向速度场在频率域的特性。

1　数值方法

1.1定常计算

定常模拟工具是三维定常Denton程序[11]，该程序在本课题组所做研究中得到了广泛采用[12-15]。采用纯H型网格显式时间推进求解雷诺平均N-S方程，空间离散采用中心差分格式，并进行流向、径向和周向的光顺以提高稳定性，采用3层多重网格来加速收敛；湍流模型为混合长度模型；转静界面采用Denton发展的掺混面技术[16]，保证交界面上下游的流量通量、动量通量及能量通量守恒。

1.2非定常计算

计算域的选取采用了简单且广为使用的“模化叶片数”方法，便于周期边条的处理。在核心算法不改变的前提下，采用双重时间步法[17]在定常程序的平台上添加了物理时间步的循环，迭代过程中通过监测第2排叶片进口处的压力、速度以及计算域出口流量的脉动来判断收敛与否。

1.3快速傅里叶变换

本文的非定常计算结果中，空间每点非定常时变曲线分成90个离散点，在非定常计算收敛后，经二次Lagrange插值到均匀分布的128(即27)个点，而后进行快速傅里叶变换(Fast Fourier Transform, FFT)计算，保存前3阶谐波的实部和虚部，并计算出各阶谐波的幅值。

2　三维跨声速多级压气机算例

2.1算例介绍

该三维多级算例是一个两级高压压气机。为便于进行非定常计算对叶片数进行了调整，调整后一级转子(R1)、一级静子(S1)、二级转子(R2)、二级静子(S2)的叶片数分别为：42、63、42和63。非定常计算时采用叶片数模化的方法每排通道数分别为2、3、2和3。

网格：图1为S1面网格示意图。如图1所示，采用了Denton式样的纯H型网格，在前尾缘处和叶片表面进行局部加密，周向和径向网格点数均为37，轴向网格点数分别为135、115、115和135。对交界面处网格进行周向均匀化以提高非定常计算时该处的插值精度。转子R1和R2计算域内叶尖间隙的处理采用“削尖”的简单做法，间隙内分配了两道网格。

图1　S1面网格示意图Fig.1　Sketch map of grid in S1 plane

边界条件：进口给定总压168 000 Pa，总温340.0 K，进口切向气流角0°，进口径向气流角根据子午面通道斜率给定，出口给定轮毂静压360 000 Pa。

2.2定常计算

图2是S3面内流量平均的熵值S沿轴向的变化趋势，横坐标是轴向计算站序号，4个方框代表4个叶片区域，MIXPLANE 1～3分别代表掺混面R1/S1、S1/R2、R2/S2。从图2可见熵值呈单调上升趋势，在掺混面处有小幅跳跃，在标号A和B附近有较大的斜率，分别和叶中截面的相对马赫数云图(图3)中的激波位置对应。

图2　熵值沿轴向的变化Fig.2　Axial variation of entropy

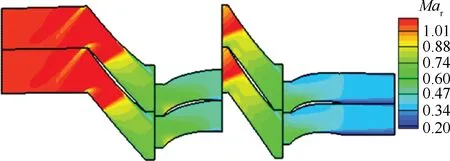
图3　叶中截面的相对马赫数Mar云图Fig.3　Contour of relative Mach number Mar at mid-height section in mid-span

由图3可以看出，R1中超声速来流经过一道脱体激波后变为亚声流，经过前缘圆角后在吸力面上重新加速为超声速流，并发出一系列膨胀波，最后以一道强的正激波结尾再次降为亚声流。因为计算状态为近失速点，R2中的激波已经被推出叶栅通道，由此可以推断该压气机的R2是最先失速级。

图4是叶中截面的熵值云图。由图4可以看出，转子吸力面上附面层沿流向逐渐增加，尾迹中熵值最大，经过掺混面处的周向掺混后静子主流区的熵值较转子有所增加，但静子尾迹的熵值较转子尾迹的小。

图4　叶中截面的熵值云图Fig.4　Contour of entropy at mid-height section

图5是第2级静子进口和出口处的周向流量平均参数沿径向的变化，限于篇幅，这里只选择总压和绝对马赫数。横坐标R*是无量纲的半径，0代表轮毂处，1.0代表机匣处。

从图5(a)的总压径向分布可以看到，该两级算例的径向分布较为复杂，表现为存在两个极大值点，这是多级叶排内流动复杂性的一种反映。因为端壁附面层的摩擦损失，在近端壁处总压较低；静子出口处的总压曲线较转子出口的要低，反映了静子中的流动损失；静子出口处的总压径向分布较进口波动幅值降低，则是静子中径向掺混的结果。

从图5(b)的绝对马赫数Maa径向分布可以看到，经过了静子的减速扩压，出口马赫数相比进口大幅降低。因子午面速度在静子前后没有太大的变化，可以认为绝对速度的降低主要体现在切向速度分量上。

图5　周向流量平均参数沿径向的变化Fig.5　Radial variation of circumferential mass-averaged parameters

2.3非定常计算

非定常计算采用Jameson提出的双重时间步推进，每个周期分为90个物理时间步，每个时间步内的最大虚拟迭代步数设为100。图6为邻近R1/S1掺混面位置，R1出口和S1进口处的轴向速度的时变曲线。图中Vx为轴向速度。由图6 可知，R1受到下游叶排的压力势干扰，S1受到上游叶排的尾迹干扰，使得轴向速度呈现出波形性，且周期性较好。这两个考察点距离很近，轴向速度波动幅值也相差不大，但由于分属转子和静子的计算域，所以R1出口的监测点实际上是在随转子转动而转动的，这就是S1进口监测点的非定常轴向速度脉动幅度大的原因。

图7(a)给出了某固定物理时刻非定常流动的熵分布等值线图，图7(b)是S1和R2交界面处的局部放大图。在S1中可以看到上游转子尾迹在静子中的发展，以及与静子叶表附面层的相互作用；在R2中同时存在R1(如图7(a)所示)和S1的尾迹(如图7(b)所示)；同样的，在S2中也可同时观察到S1和R2的尾迹，但因S1尾迹亏损深度较浅，兼在R2中的尾迹与主流的掺混，所以S2中的S1尾迹不是很清晰。由此可以推论，在压气机的Clocking研究中会发现R-R的Clocking效应比S-S大，文献[18]经过Clocking数值研究也得到了类似的结论。

图6　轴向速度Vx的时变曲线Fig.6　Variation of axial velocity Vx with time

图7　非定常流动的熵值等值线Fig.7　Isoline of entropy of unsteady flow

在得到各个物理时刻的流场之后，直接代数平均便可以得到非定常时均场，图8所示为时均场相对马赫数云图。可以看到与定常计算的结果相近，在近失速工况时R2的激波面已经被推出叶排通道。

图8　时均场相对马赫数Mar云图Fig.8　Contour of time-averaged Mar

3　频域分析

3.1叶中S1截面分析

图9给出了各叶排非定常轴向速度的1阶谐波的实部分布云图，后文中如果不特别指明，研究变量都默认为轴向速度。需要说明的是，本文所述1阶谐波对应的频率是上下游叶排的通过频率(Blade Passing Frequency， BPF)，2阶谐波对应的频率是上下游叶排的通过频率的2倍频，其余以此类推。因此，虽然4排叶片的幅值云图绘制在一起，但它们所对应的BPF各自意义不同，尽管数值上有相同的巧合情况。本文的非定常算例为2∶3∶2∶3，对于S1、R2来说，上下游的BPF是一致的，所以实部分布云图体现了上游叶排的尾迹干扰和下游叶排的势干扰，否则，仅仅一个叶排也需要分成两幅图才能分别表征上游叶排尾迹干扰的1阶谐波云图和下游叶排势干扰的1阶谐波云图。

图9中有4排叶片，从后往前逐一分析可以看出， S2中图像呈现出条带的形状且其走向和上游尾迹的方向相同，这是由于：①尾迹某瞬时扫过的区域具有一个特点，在以时间为横坐标的流场参数时变曲线上初始相位角近似相同；② 1阶谐波的实部/虚部是幅值与该角度的正弦函数/余弦函数的乘积，所以该角度在FFT分解时会保证实部(或虚部)在尾迹扫过区域的取值近似相等。条纹呈正负交替的出现也是正余弦函数值有正有负的特点所致。

图9　叶中截面1阶谐波实部VR的分布Fig.9　Real part of the 1st rank harmonic VR at mid-height section　

S2静子计算域内有5～6条条带，这点可以从流场非定常特征参数计算出来，S2计算域的轴向长度约0.122 245 m，轴向速度约150 m/s，尾迹通过时间大致为8.15×10-4s，而R2转子尾迹扫掠频率为6 678 Hz(9 540×42/60)，则S2计算域内尾迹条数为两者的乘积5.44，与频域中的条带数吻合。

同样的，R2中图像呈现出条带的形状而且其走向和S1尾迹的方向相同。R2计算域的轴向长度约0.066 567 m，轴向速度约170 m/s，尾迹通过时间大致为3.916×10-4s，而S1尾迹相对扫掠频率为10 017 Hz(9 540×63/60)，则R2计算域内尾迹条数为两者的乘积3.92，与频域中的4条条带相吻合。

S1中图像呈现出条带的形状较上述两排叶排要复杂一些，这是因为S1除受到上游叶排的尾迹干扰外，还受到下游R2叶排前缘激波的强烈上传势干扰的影响，如图10 S1、R2的静压云图所示，而R2、S2叶排则未受此影响。S1计算域中前半部分条带的走向和R1尾迹的方向相同，后半部分条带的走向则和R2前缘激波的走向相同。

图10　某非定常瞬时S1、R2内的静压ps云图Fig.10　Contour of static pressure ps in S1 and R2 at some unsteady time

而R1中没有尾迹干扰，出口处可见下游静子受到微弱的势干扰。

图11(a)给出了叶中截面1阶谐波的幅值分布云图。总体上R1的进口和S2的出口因远离脉动源，脉动幅值较弱。S1通道中因感受到上下游叶排的耦合干扰，脉动幅值最大，尤其是在出口，因本文算例是高速跨声速压气机的近失速点工况，波前马赫数较强，所以前伸激波导致的压力势干扰也随之加强。图11(b)、图11(c)各自给出了叶中截面的2阶、3阶谐波的幅值云图。对比可以看出，随着谐波阶次的升高，脉动幅值降低，周向的不均匀性减弱；通过S1通道中进出口处的脉动幅值对比，还可以看出非定常势干扰的谐波分量随谐波阶次的增加而降低的速度较尾迹干扰要快一些。在三阶谐波幅值云图上进口处已经明显高于出口。图中：Vx,1，Vx,2和Vx,3分别为轴向速度1、2和3阶谐波幅值。

图11　叶中截面1阶、2阶与3阶谐波的幅值云图Fig.11　Amplitude contours of the 1st, 2nd and 3rd rank harmonic at mid-height section

图12绘制了S2周向中间位置轴向速度1、2、3阶谐波幅值沿轴向的变化曲线。能够看到：① 进口处随着谐波阶次增加，脉动幅值降低；② 在脉动发展过程中，随着谐波阶次增加，幅值衰减的速度也加快；③ 幅值沿轴向的振荡幅度随谐波阶次增加而降低；④ 在出口处，各阶谐波脉动幅值并不为0，尤其是1阶谐波的分量还较大，这是出口的数值反射的缘故；⑤ S2叶排中存在轴向、周向甚至还有径向的压力梯度，且存在尾迹与附面层的相互作用，在这些复杂因素的影响下，兼有出口处数值反射的因素，导致1阶谐波的幅值沿着流向并不单调“衰减”。图13给出的叶中截面非定常脉动压力1阶谐波的幅值云图可以较为直观地观察到计算域出口的数值反射；文献[10]对NUMECA计算得到的单级跨声速轴流压气机非定常算例也观察到该现象。

图12　S2轴向速度前3阶谐波幅值沿轴向变化Fig.12　Axial variation of amplitudes of the first three rank axial velocity harmonics in S2

图13　叶中截面非定常脉动压力的1阶谐波幅值Fig.13　Amplitude of 1st rank harmonic of unsteady fluctuating pressure at mid-height section

图14绘制了S1进口轴向第3道网格处轴向速度1阶谐波幅值沿周向的变化曲线。该处的轴向速度脉动主要来源于上游R1的尾迹干扰，下游的势干扰相对较小。如果转子与静子之间的轴向间距足够大，那么静子计算域进口处的轴向脉动速度沿周向就是不变的。图14中的非定常速度的脉动幅值的变化就是因为受到静子的势干扰，所以其波峰、波谷的位置和静子叶栅通道的周向位置关联。确定应力建模时，如果采用Rhie[19-20]提出的简单的不考虑周向变化的建模方法会引入较大的误差。还可以看到，该曲线呈现出较好的周期性，没有出现Adamczyk[21]通道平均理论中的“通道差异”，则是因为S1和S2的叶片数完全相等，导致频域内的流场无差异。

图14　S1轴向速度1阶谐波幅值沿周向变化Fig.14　Circumferential variation of amplitude of the 1st rank axial velocity harmonic in S1

图15是R1出口倒数第3道网格处，叶栅中部位置的轴向速度经FFT后得到的频谱图。R1进口对应整个计算域的进口处的速度脉动很小不再给出。图15中：小方框内的数字为对应频率的序号，其中采样频率为427 392 Hz。频率分辨率设定为417.375 Hz，各序号对应的频率值为序号与该值的乘积。R1感受到S1的叶片扫掠频率(BPF)对应序号为24(对应频率值为24×417.375=10 017 Hz，以此类推)；感受到R2的叶片BPF对应序号为16，相应的，序号48代表S1 BPF的2倍频；序号32代表R2 BPF的2倍频，以此类推。由图15可见，出口处受S1 BPF的基频影响最大，脉动幅值为11.15 m/s，而R2非定常势干扰传到此处已经严重衰竭，R2 BPF基频对应的脉动幅值仅为0.41 m/s。

图16是S1进口第3道网格和出口倒数第3道网格处，叶栅中部位置的静压经FFT后得到的频谱图。后续2个叶排的监控点相对位置均与此相同。S1感受到R1的尾迹扫掠频率对应序号为16；因为R1、R2的叶片数目相等，感受到R2的势干扰扫掠频率对应序号亦为16，所以图中的振幅是上下游干扰的叠加。从进口的轴向速度频谱可以看出，BPF基频对应的幅值为26.70 m/s，因为此处距离R1出口的监控点较近，根据上文分析，该处R2激波引发的势干扰已经大大衰弱，此处振幅主要由R1的尾迹扫掠引起；S1出口轴向速度频谱中BPF基频对应的幅值为20.11 m/s，则主要由R2激波引发的势干扰所致。

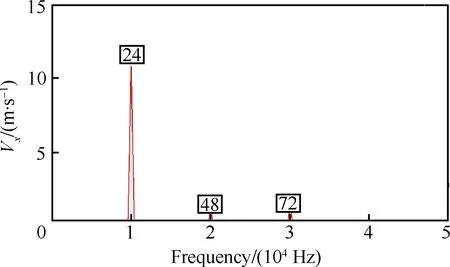
图15　R1出口的轴向速度频谱Fig.15　Spectrum of axial velocity at outlet of R1

图16　S1进口和出口的轴向速度频谱Fig.16　Spectrum of axial velocity at inlet and outlet of S1

图17是R2进口和出口处叶栅中部位置的轴向速度FFT后得到的频谱图。因为S1、S2的叶片数目相等，R2感受到上下游叶片扫掠频率对应序号均为24，所以图中的振幅是上下游干扰的叠加。出口处受S1和S2 BPF的基频(序号24)影响最大，脉动幅值为4.85 m/s，远小于S1出口的1阶谐波分量；而R1尾迹干扰传到此处已经严重衰竭，R1 BPF基频(序号16)对应的脉动幅值仅为1.38 m/s。

图18是S2进口处叶栅中部位置的轴向速度FFT后得到的频谱图。可以看到，S2感受到距离最近的R2的叶片扫掠频率对应序号为16，对应位置处的振幅也是最大的；在序号24处感受到了S1尾迹的微弱影响，对应的幅值仅为0.82 m/s，出口监测点位于计算域出口倒数第3道网格，存在明显的数值反射，此处不再分析。

图17　R2进口和出口的轴向速度频谱Fig.17　Spectrum of axial velocity at inlet and outlet of R2

图18　S2进口的轴向速度频谱Fig.18　Spectrum of axial velocity at inlet of S2

3.2S3截面分析

图19给出了S1、R2和S2进口处S3面(逆流向看)内的轴向速度1阶谐波幅值云图。由于R1进口处的轴向速度1阶谐波幅值很小，因此本文没有给出。如前所述，图像中呈现出通道的周期性；幅值沿周向波动，且最大值点的位置也随着径向位置的变化而变化，在图14中介绍过波峰波谷的位置更多受下游叶排的势干扰，图20则给出了同样视角的S2叶片的叶型。可以看到图19(c)中周向最大值点沿径向的走势与S2叶型的“C弯”一致，验证了上述分析。同样，从图19(a)也可以分析出S1叶型也设计成“C弯”，限于篇幅，本文不再给出S1的叶型示意图。

图19　S1、R2和S2进口1阶谐波幅值云图Fig.19　Amplitude contours of the 1st rank harmonic at inlet of S1， R2 and S2

图21给出了R1、S1和R2出口处S3面(逆流向看)内的轴向速度1阶谐波幅值云图。S2出口处存在数值反射，不再给出。图21(a)、图21(c)的转子叶栅通道中，左边为压力面的延伸区，右边为吸力面的延伸区(可参考网格示意图1)，两图的最大值点都位于吸力面与轮毂面的角区处，反映出该处的轴向速度受下游静子叶排的势干扰影响最大；但从绝对数值上看，较图21(b)中S1出口幅值的最大值都小得多；图21(b)中总体数值高则归因于R2前缘处强烈的激波干扰。

图20　S2叶型Fig.20　Profile of S2

图21　R1、S1和R2出口1阶谐波幅云图Fig.21　Amplitude contours of the 1st rank harmonic at outlet of R1, S1 and R2

图21(b)的静子叶栅通道中，左边为吸力面，右边为压力面。可以看到1阶谐波幅值在沿径向高度增加而增加的同时，周向也呈现出强烈的不均匀性:在低叶高区域，与转子叶栅通道中一致，吸力面处的脉动幅值更大一些；而在高叶高区域，当受到下游激波的强烈干扰时，压力面处的脉动幅值更高一些，结合图10的压力云图可以看到，这是因为S1压力面是下游激波势干扰的“迎风面”的缘故。

3.3其他参数分析

以上都是对轴向速度频域图谱的分析，其他如切向速度、径向速度与此类似，这里不再给出。图22给出了各叶中截面的静温、总温、密度、总压的1阶谐波幅值云图。从图22(a)、图22(b)可以看出，静温、总温谐波幅值云图与图11(a)的轴向速度的谐波幅值云图相类似。从图22(c)、图22(d)可以看出，密度、总压谐波幅值云图与图11(a)的轴向速度的谐波幅值云图并不一致，而是与图13给出的静压的1阶谐波幅值云图相类似，尤其是在S1叶栅通道中表现得最为明显。究其原因，是因为S1通道内气流受到强烈的R2前缘激波的势干扰所致。激波对总温没有影响，而在总温保持不变的情况下，静温和速度保持联动关系，这就是静温的频域图谱与轴向速度的谐波幅值云图类似的原因；而气流经过激波后，总压降低，静压升高，密度随之增大，三者保持联动关系，这就是S1叶排中密度、总压频域云图与静压的谐波幅值云图高度类似的原因；在S2叶排中因为没有S1那种强烈的激波干扰，仅受到上游叶排的尾迹干扰，所以谐波幅值云图与轴向速度相类似，条带与尾迹走向保持一致。

图22　叶中截面静温、总温、密度和总压的1阶谐波幅值云图Fig.22　Amplitude contours of the 1st rank harmonic of static temperature, total temperature, density and total pressure at mid-height section

4　结　论

通过对两级跨声速压气机典型截面非定常流场向频域的转换，在国内率先得到了较为系统的多级跨声速压气机内部各流场参数的频谱特征，分析得到以下结论：

1) 通过对非定常频域图谱的研究，从一个全新的视角来分析非定常流场，可以看到一些在时域流场中很难直观看到的现象，如出口处的数值反射。

2) 非定常轴向速度受尾迹的影响非常大，且在沿流向发展过程中，随着谐波阶次增加，幅值沿轴向的振荡幅度降低，幅值衰减的速度也加快。

3) 各叶排进口1阶谐波幅值在S3面内的分布受到下游叶排的势干扰，周向最大值点沿径向的走势与叶型的径向弯曲一致。

4) 本文算例中静温、总温1阶谐波幅值云图与轴向速度的频域云图相类似，而气流密度、总压的1阶谐波幅值云图与气流静压的1阶谐波幅值云图相类似，在S1中表现得最为明显，是由于S1通道内气流受到强烈的R2前缘激波的势干扰所致。

[1]HE L, NING W. Efficient approach for analysis of unsteady viscous flows in turbomachines[J]. AIAA Journal, 1998, 36(11)： 2005-2012.

[2]CHEN T, VASANTHAKUMAR P, HE L. Analysis of unsteady blade row interaction using nonlinear harmonic approach[J]. Journal of Propulsion and Power, 2001, 17(3)： 651-658.

[3]ALEXANDER P, BORIS L. Small disturbance navier-stokes method: Efficient tool for predicting unsteady air loads[J]. Journal of Aircraft, 2006, 43(1): 17-29.

[4]GABRIEL S, MEHMET I,ABDULNASER I, et al. A multi-blade-row linearised analysis method for flutter and forced response predictions in turbomachinery： ASME GT2006-90789[R]. New York: ASME, 2006.

[5]MAGNUS S, ERIKSSON L E. Modeling unsteady flow effects in a 3d transonic compressor: ASME GT2005-68149[R]. New York: ASME, 2005.

[6]VILMIN S, LORRAIN E, HIRSCH C. Unsteady flow modeling across the rotor/stator interface using the nonlinear harmonic method: ASME GT2006-90210[R]. New York: ASME, 2006.

[7]刘波, 王雷, 黄建. 非线性谐波法在双级对转压气机中的进一步校检[J]. 航空动力学报, 2013, 28(6)： 1333-1341.

LIU B,WANG L, HUANG J. Further validation of nonlinear harmonic method in two-stage counter-rotating compressor[J]. Journal of Aerospace Power, 2013,28(6)：1333-1341 (in Chinese).

[8]王英锋， 胡骏， 罗标能， 等． 上游叶片尾迹对转子叶片非定常表面压力频谱特性的影响研究[J]． 航空动力学报， 2006， 21(4): 693-699．

WANG Y F, HU J , LUO B N, et al. Effects of the up-stream blade wakes on the spectrum of rotor blade unsteady surface pressure[J]. Journal of Aerospace Power, 2006, 21(4): 693-699 (in Chinese).

[9]魏宝锋， 金东海， 桂幸民． 离心叶轮与扩压器相互干扰数值模拟[J]． 航空学报， 2012， 33(7)： 1173-1180.

WEI B F, JIN D H, GUI X M. Numerical simulation of impeller-diffuser interaction in centrifugal compressor[J]. Acta Aeronautica et Astronautica Sinica,2012,33(7):1173-1180 (in Chinese).

[10]赵军， 柳阳威， 刘宝杰. NASA67级非定常流场的频域分析[J]. 航空动力学报, 2007, 22(8)： 1371-1377.

ZHAO J, LIU Y W,LIU B J. Frequency-domain analysis of NASA67 unsteady flow field[J]. Journal of Aerospace Power,2007, 22(8)： 1371-1377 (in Chinese).

[11]DENTON J D. The use of a distributed body force to simulate viscous effects in 3D flow calculations: ASME 86-GT-144[R]. New York: ASME, 1986.

[12]陈懋章. 风扇/压气机技术发展和对今后工作的建议[C]//21世纪航空动力发展研讨会.北京:中国航空学会动力专业分会, 2000: 74-87.

CHEN M Z. Fan/Compressor technology development and the suggestions on future research[C]//Symposium on the Proceedings of Aero-engine in 21st Century. Beijing: Propulsion Branch of CSAA, 2000: 74-87 (in Chinese).

[13]刘宝杰， 邹正平， 严明, 等. 叶轮机计算流体动力学技术现状与发展趋势[J]. 航空学报, 2002, 23(5)： 394-404.

LIU B J , ZOU Z P , YAN M， et al. Present status and future development of CFD in turbomachinery[J]. Acta Aeronautica et Astronautica Sinica, 2002, 23(5)： 394-404 (in Chinese).

[14]邹正平, 徐力平. 叶轮机三维非定常流动数值模拟的研究[J]. 航空学报, 2001, 22(1): 10-14 .

ZOU Z P, XU L P.Numerical study of the 3-D unsteady flow in turbomachinery stages[J]. Acta Aeronautica et Astronautica Sinica, 2001, 22(1): 10-14 (in Chinese).

[15]周燕佩, 徐力平. 计算流体动力学在航空叶轮机械中的应用[C]//21世纪航空动力发展研讨会. 北京: 中国航空学会动力专业分会, 2000: 100-104 .

ZHOU Y P, XU L P. CFD application on aero-turbomachinery[C]//Symposium on the Proceedings of Aero-engine in 21st Century. Beijing: Propulsion Branch of the CSAA, 2000: 100-104 (in Chinese).

[16]DENTON J D. The calculation of three-dimensional viscous flow through multistage turbomachines[J]. Journal of Turbomachinery, 1992, 114(1): 18-26.

[17]JAMESON A. Time dependent calculation using multigrid with application to unsteady flows past airfoils and wings: AIAA-1991-1596[R]. Reston: AIAA, 1991.

[18]HE L. Analysis of rotor-rotor and stator-stator interferences in multi-stage turbomachines[J]. Journal of Turbomachinery, 2002, 124(5): 564-571.

[19]RHIE C M. Development and application of a multistage navier-stokes solver, Part 1: Multistage modeling using body-forces and deterministic stresses: ASME paper 95-GT-342[R]. New York: ASME, 1995.

[20]RHIE C M. Development and application of a multistage navier-stokes solver, Part 2: Application to a high pressure compressor design: ASME paper 95-GT-343[R]. New York: ASME, 1995.

[21]ADAMCZYK J J. Model equation for simulation flows in multistage turbomachinery: ASME paper 85-GT-226[R]. New York: ASME, 1985.

赵军男， 博士， 高级工程师。主要研究方向： 叶轮机械内复杂流动研究。

Tel: 0838-5182503

E-mail: 491452660@qq.com

刘宝杰男， 博士， 教授， 博士生导师。主要研究方向： 叶轮机械内气动热力学研究。

Tel: 010-82316419

E-mail: liubj@buaa.edu.cn

Frequency-domain analysis of unsteady flow in multi-stagetransonic compressor

ZHAO Jun1, LIU Baojie2,*

1. Aviation Engineering Institute，Civil Aviation Flight University of China， Guanghan618307, China 2. School of Energy and Power Engineering，Beihang University, Beijing100083, China

Three-dimensional unsteady solver has been developed based on three-dimensional Denton steady solver. Steady and unsteady numerical simulation have been conducted on multi-stage transonic compressor near stall point，and then frequency-domain analysis of unsteady flow field have been conducted on some typical radial sections. Frequency-domain research makes us analyze the unsteady flow field from a new perspective, and we can see some of the phenomena that are difficult to see in the time domain. The effect of the wake on axial velocity is very large, and in the developing process along the flow, with the increase of harmonic order, axial oscillation amplitude reduces, and the attenuation speed of the amplitude is also accelerating. The distribution of the 1st harmonic amplitude in the S3 plane is disturbed by the potential interference of the downstream blade row, and the maximum value point in the circumferential direction along the radial direction shaped as the blade profile. The effect of the wake on flow density, static pressure and total pressure is small, while the air static temperature and total temperature are greatly affected by the wake.

aero-engine; transonic; compressor; unsteady calculation; frequency analysis

2015-10-22； Revised： 2015-12-16； Accepted： 2016-01-08； Published online： 2016-01-1216:13

s： National Natural Science Foundation of China (51306201)； Natural Science Project of Sichuan Provincial Department of Education (16ZB0035); Science Research Foundation of Civil Aviation Flight University of China (J2014-38， J2015-28)

. Tel.： 010-82316419E-mail: liubj@buaa.edu.cn

2015-10-22； 退修日期： 2015-12-16； 录用日期： 2016-01-08；

时间： 2016-01-1216:13

www.cnki.net/kcms/detail/11.1929.V.20160112.1613.004.html

国家自然科学基金 (51306201); 四川省教育厅自然科学科研项目 (16ZB0035); 中国民用航空飞行学院科学研究基金 (J2014-38， J2015-28)

.Tel.： 010-82316419E-mail: liubj@buaa.edu.cn

10.7527/S1000-6893.2016.0012

V231.3

A

1000-6893(2016)06-1798-11

引用格式： 赵军， 刘宝杰． 跨声速多级压气机中的非定常流场频域分析[J]． 航空学报, 2016, 37(6): 1798-1808. ZHAO J, LIU B J. Frequency-domain analysis of unsteady flow in multi-stage transonic compressor[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(6): 1798-1808.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

URL： www.cnki.net/kcms/detail/11.1929.V.20160112.1613.004.html