例谈导数应用中的转化策略

◇　江苏　蒋丽丽

(作者单位：江苏省张家港市乐余高级中学)



例谈导数应用中的转化策略

◇江苏蒋丽丽

证明不等式或解不等式恒成立问题是函数综合问题的常考题型,解题方法主要是构造函数、利用导数求函数最值．但若根据所给的函数直接构造,常使函数单调性的求解陷入困境．这就需要我们在求导前对函数进行等价转化．下面引例1说明．

(1) 当x∈(0,+∞)时,f(x)>0恒成立,求a的取值范围.

1　分离参数

第(1)问求解中若由f(x)=aex-x-1>0直接求fmin(x)的最小值,则需要对a进行分类讨论,过程烦琐．对于含参不等式恒成立问题的求解,可根据函数的结构特征考虑将参数分离出来,进而可将函数具体化．注意参数分离的过程要具有等价性．

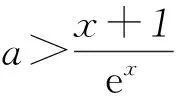
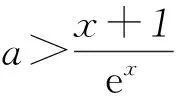
另外对于某些复杂的含参问题,若参数不能单独分离出来,可考虑将含参式整体分离.

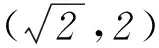
f′(x)=[-ax2+(2a2-2)x+2a]eax,

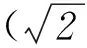
2　分离函数

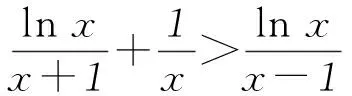
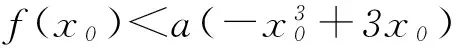
当x≥1时,ex-1/ex>0,x2-1≥0.又a>0,故g′(x)>0,所以g(x)是[1,+∞)上的单调递增函数,g(x)在[1,+∞)上的最小值是g(1)=e+e-1-2a.

此时无法直接比较ea-1与ae-1的大小,可对2式同时取自然对数,即比较a-1与(e-1)lna的大小,因此可构造以a为主元的函数．

当a=e时,ea-1=ae-1;当a∈(e,+∞)⊆(e-1,+∞)时,h(a)>h(e)=0,即a-1>(e-1)lna,故ea-1>ae-1.

3　二次求导

针对导函数的符号不易判断的情况,可再次构造函数,即设导函数为新的函数,或取导函数的局部(决定导数正、负符号的部分)来构造新函数,将问题转化为求新函数的最值问题,进而利用二次求导来证明该导函数在定义域上恒正或恒负,求出导函数的最值,判断导函数的符号后得到原函数的单调性．

续解:求导得

此时导函数的零点仍不可求,须继续寻找突破策略．

设t(x)=ex-x-1,则t′(x)=ex-1.令t′(x)=0,得x=0.所以t(x)在(-∞,0)上单调递减;在(0,+∞)上单调递增.当x=0时,tmin(x)=f(0)=0.

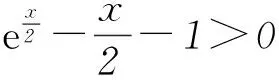
总之,在运用常规思路对上述问题求解中,要善于挖掘题目隐含条件,将原不等式进行等价变形,这是化简运算的一种有效途径．因此平时学习中要对所遇到的问题加以整理概括,才能不断提高我们分析问题与解决问题的能力．

(作者单位：江苏省张家港市乐余高级中学)