广义相对论中的时空结构
王晓松
(天津市南开区职工大学,天津 300102)
广义相对论中的时空结构
王晓松
(天津市南开区职工大学,天津300102)
广义相对论中的时空结构不同于狭义相对论中的时空结构,更不同于经典物理学中的时空结构,它说明宇宙中的时空结构可能是相当复杂的。这篇文章阐述广义相对论中的时空结构与以往所有的时空结构的基本不同之处。
时空结构;广义相对论;引力场方程;Schwarzschild解;间隔
广义相对论中没有可以统一使用的时空框架。每一个局域的时空状态都不相同。这里是用黎曼度规描绘引力时空的特性。于是,无限邻近的两个事件的间隔是:
ds2=-c2dτ=gμνdxμdxν
(1)
一、局域引力场的设计
我们没有必要处处都进行复杂的演算。设计一个局域的引力场。不要一提起引力场就想到地球的引力场。任何局域的引力场都有它自己的重力加速度,都符合自由落体运动的规律。场内的任何物体如果不受其他因素的干扰,都会沿着重力加速度的方向运动。
(2)
同时,固定于引力场中的坐标系为,这个坐标系也应当是正交的,于是就有:
ds2=-c2dτ2=-(dx0)2+(dx1)2+(dx2)2+(dx3)2(3)
下面我们做进一步的设计:因为是局域场,所以两个坐标系的时间变量可以认为是基本一致的,也就是:
(4)
再根据自由落体运动的规律,两个坐标系的关系应当如下:
(5)
这是由于这两个坐标系只有属于方向相同,但是做自由落体运动。其他的坐标分量则没有什么不同。
对上述坐标关系式求导,得到下列关系式:
(6)
将(6)带入(2),就有:
(7)
根据(5)式,自由落体运动所产生的位移:
(8)
另一方面,自由落体运动的系统其重力势能的变化为:
(9)
为纯粹地反映出引力场的性质,这里去掉了具有检验性质的自由落体运动的物体的质量,定义出引力势的概念,即是:
(10)
如果定义自由落体运动开始时的引力势为0,物体运动到引力场中某一位置时的引力势是,自由落体运动引力势是降低的,引力势能是减少的,所以有:
(11)
g2t2=-2φ
(12)
将(12)带入(7),可以得到:
(13)
对比一般意义上的间隔定义式:
ds2=-c2dτ=gμνdxμdxν
(1)
在这里,不为0的度规张量分量有(其余分量均为0):
(14)
这里需要说明的是,指标μ=0,1,2,3,指标ν也一样。但如果指标中不考虑时间分量的话,就定义指标A=1,2,3,指标B也是如此。这些问题以后不再赘述。
把任何引力场局域化,就可以得到沿着引力方向的坐标轴的度量张量分量与唯一的客观参数——引力势φ之间的关系。
二、引力场中引力势与时间的关系
根据:
(13)
我们可以想象引力场中的物体在某种条件下不发生任何位移,即:
dx1=dx2=dx3=0
(15)
但无论如何,一定有:
(16)
因为时间的流动是挡不住的。如果我们专门考虑这种情况,根据(13)、(14)和(1),就会有:
(17)
于是就有:
最后得到:
(18)
也就是说,广义相对论中时间的流动速度与引力有关,引力越强,则时间流动越慢。一旦引力为0,就回到了狭义相对论的状态。时间流动的快慢只与物体运动的速度有关。
三、引力场中引力势与空间的关系

(19)
在没有空间位移的条件下,考虑到间隔本身的原始定义,本引力场的固有时为:
(20)
于是,本次运动的固有时是:
(21)
根据(21),引力场中A点与B点之间的空间距离是:
(22)
再次考虑到间隔本身的原始定义,在此定义中,时间维度与空间维度是减法关系,但间隔中的时间正是以光速穿过其空间距离所用的时间。因此对于光讯号而言,这种想减的结果就是〇,所以对于光讯号而言:
ds2=gμνdxμdxν=g00(dx0)2+g0Adx0dxA+g0Bdx0dxB+gABdxAdxB=0
(23)
因为A和B同为非时间维度的指标,将相关项缩并,就得到:
g00(dx0)2+2g0Adx0dxA+gABdxAdxB=0
(24)
把(24)看做一个以(dx0)为变量的一元二次方程,解之既得:
(25)
这样就有:
(26)
(27)
其中,根号内第一项的第二小项将指标A更换成了指标B,这是合乎数学原则的。
(28)
这是在上式中将-dxA代换dxA所得到的光讯号从B⟹A时的结果,当然也进行了必要的,合乎逻辑的指标代表。
(27) +(28)得到:
(29)
根据(22):
(30)
其中:
(31)
(32)
现在再次考虑到普适的局域引力场中的自由降落体系的问题,根据:
(14)
CAB不为0的分量只有:
(33)
这样,根据(31),就有:
(34)
这是引力沿着x2方向运动时的情况。
由(34),由于一般意义上以远离引力源的位置的引力势为零,而物体在引力的作用下运动,引力势处于减量,这样引力势一般取负值。于是:
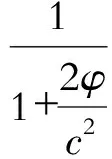
(35)
这样就有:

(36)
就是说引力越强之处,任意两点间的距离因为空间弯曲而变长了。引力越强,空间就越弯曲,任意两点之间的距离就越长。
四、归纳与总结
一般意义下的静态引力场(引力源不转动或者转动很慢),物体在引力的作用下做自由落体运动。只是其重力加速度在不同的引力源周围不同而已。同时,只要坐标设置合理,比如设置合理的球坐标(因为引力源一般可以近似地被看做是球状),那么参与运动过程的坐标维度一般只有两个,即时间维度和某一个空间维度。联想到Einstein方程的Schwarzschild解,
(37)
再联系(36)和(18),可以看出Schwarzschild解正是反映了本文所论述的广义相对论条件下的时空结构。本文不是要去分析Schwarzschild解,关于Schwarzschild解的问题,本人已经在《成功(教育版)》 -2008年9期发表的论文《论席瓦西尔(Schwarzschild)外部解》中做过详尽分析。
本文的目的就是通过其他的角度,经过分析说明:在引力场中,由于引力的作用,时间的流动会变慢,空间会扭曲,因而空间中任意两点间的距离会变长。引力越大,时间流动就越慢,空间就越扭曲,因而任何两点间的距离就会变得越长。这就是广义相对论框架下的时空结构。
[1]唐肇华,刘素芸,翁甲强编著. 广义相对论导论[M].桂林:广西师范大学出版社,1997.
[2]刘辽,赵峥,田桂花,张静仪著.黑洞与时间的性质[M].北京,北京大学出版社,2008.
[3]郭世堃编著.广义相对论导论[M].成都,电子科技大学出版社,2005.
Space-time Structure in General Theory of Relativity
WANG Xiao-song
(Tianjin Staff University of Nankai District, Tianjin, 300102)
the space-time structure in general relativity is different from the space-time structure in special relativity, and it especially differs from the space-time structure in classical physics, and it shows that the space-time structure in the universe may be quite complicated. This paper elaborates the fundamental differences between the space-time structure in general relativity and all previous spatiotemporal structures.
space-time structure; general relativity; gravitational field equation; Schwarzschild interpretation; interval
2016-09-02
王晓松(1961-),男,南开社区学院,副教授。
O412
A
1673-582X(2016)11-0095-06

