桥式起重机的二自由度内模防摆控制研究
王小静,陈志梅,邵雪卷
(太原科技大学电子信息工程学院,太原 030024)
桥式起重机的二自由度内模防摆控制研究
王小静,陈志梅,邵雪卷
(太原科技大学电子信息工程学院,太原 030024)
提出一种内模二自由度的控制方法,将桥式起重机的定位防摆控制转化为对定位、绳长控制系统的伺服跟踪,并利用起重机模型的强耦合性保持摆角稳定。根据内模控制理论设计二自由度控制器将系统的抗干扰性和跟随特性分开进行控制,增强了系统的鲁棒性。使得起重机小车和吊绳快速准确到达期望位置的同时抑制负载摆动,理论分析和仿真实验证明了该方法的可行性。
桥式起重机;耦合性;防摆控制;内模控制;二自由度控制
由于受外界各种因素的干扰(如:风力、摩擦力、力矩转动等),使得起重机精确定位和防摆控制相当困难,影响了系统的稳定性和定位精度。因此对起重机定位和防摆控制方法的研究具有深远意义。文献[1-2]在模糊控制的基础上提出了变论域模糊控制,解决了论域选择的难题。文献[4]提出了一种动态滑模控制方法,通过微分环节设计新的动态滑模面,加速了起重机的定位和防摆;也有学者采用终端滑模及二阶滑模的方法解决桥式起重机的定位防摆问题[5-7]。文献[8]将神经网络控制方法应用在起重机防摆控制中,取得了较好的控制效果。但上述方法无法让系统的抗干扰性和跟随性两者同时达到最优。
内模二自由度控制是一种新型的控制方法,其设计结构简单、调节参数少,通过两个控制器对抗干扰性和跟随性分别进行控制。文献[9]将内模二自由度控制运用在不确定延迟系统中,设计前馈、反馈两个控制器,对仅有的两个参数进行了整定。文献[10]设计了基于灵敏度函数的新型二自由度控制,实现跟随性和抗干扰性完全解耦。针对非自衡被控对象文献[11-13]提出了改进的内模二自由度控制,设计控制器镇定不稳定对象,增强了系统的鲁棒性。
针对桥式起重机防摆控制现有方法的不足,本文提出了一种前馈型二自由度内模控制方法。将系统简化为对定位控制系统和绳长控制系统的伺服跟踪,并利用起重机的强耦合性,通过调节定位控制系统来消除摆角。仿真研究结果表明该方法能同时实现对起重机的定位、绳长以及摆角的控制,提高了起重机的运行效率。
1 桥式起重机的数学模型
本文研究的是在提升载荷的同时有一个水平方向移动的起重机,将空间摆运动简化为平面摆运动,即二维空间的起重机模型,该模型是研究最为广泛的模型[14-15]。如图1所示为桥式起重机的二维空间结构:
M、m分别表示小车和负载的质量,l表示绳长,x表示位移,θ表示负载的摆角,g表示重力加速度,ux、ul分别表示水平运动和提升运动的摩擦系数,fx、fl分别表示小车水平驱动力和沿绳子提升力。根据起重机工作情况,给出如下假设和要求:

图1 二维桥式起重机系统模型
(1)钢丝绳的质量相对于吊钩及重物的质量忽略不计;(2)提升钢丝绳刚度足够大,其长度变化忽略不计;根据拉格朗日方程可以得到桥式起重机的二维动力学模型为:
(1)
(2)
对式(2)进行拉氏变换可得:
(3)
(4)
(5)
其中,F(s)=Fx(s).
由公式(3)-(4)可知,桥式起重机位移和摆角之间的耦合关系,如图2所示。
2 控制器的设计
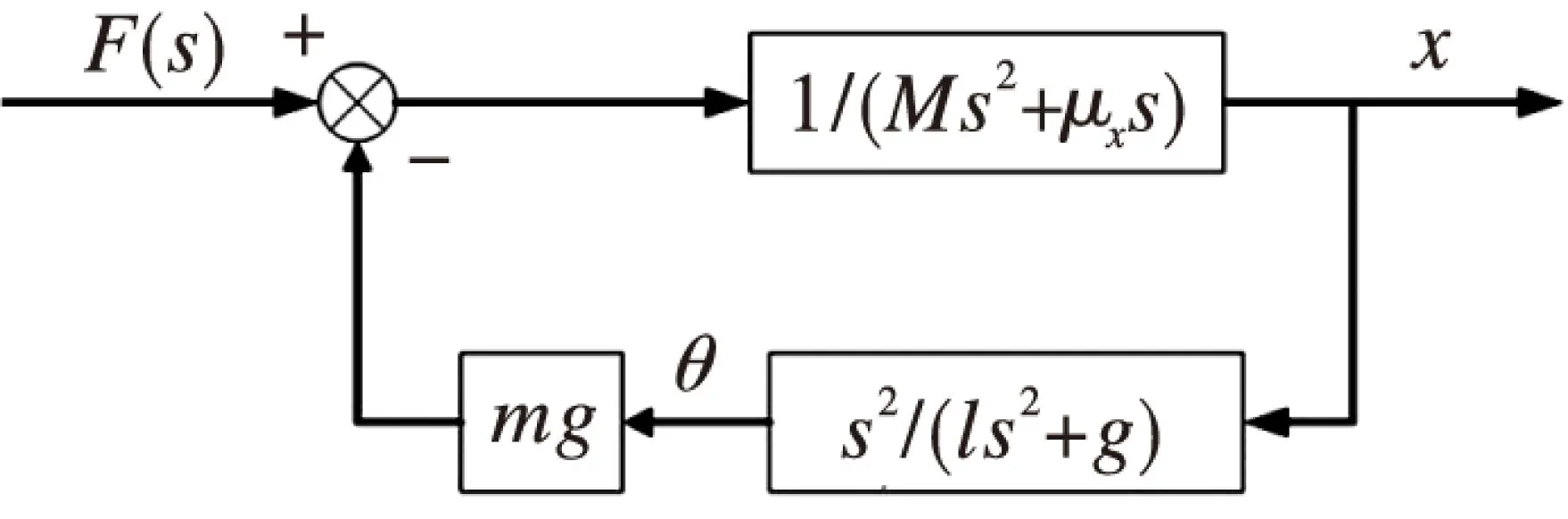
图2 桥式起重机位移摆角关系图
2.1 内模二自由度控制
内模二自由度控制由输入信号的前馈通道和按误差控制的反馈通道组成,其系统结构如图3所示,其中Q1(s)、Q2(s)为内模控制器,Gx(s)为被控对象,M(s)为对象模型,D(s)为系统的内部输入扰动,R(s)和Y(s)分别为系统的给定输入和输出。
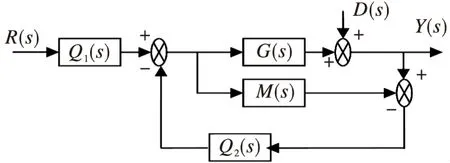
图3 内模二自由度控制结构图
由图3可知系统的输出:
(6)
(A)针对桥式起重机的绳长控制系统:
(7)
根据IMC原理,Gl(s)=Gl+1(s)Gl-(s),
Gl(s)=m/(ms2+μls),设计控制器如下:
(8)
(9)
f1(s)、f2(s)为控制器可实现因子,是一个低通滤波器,为了使起重机的绳长控制系统具有好的稳态和动态性能,本文选取:
(10)
则将式(10)代入式(8)、(9)得:
(11)
(12)
(B)针对桥式起重机定位控制系统以及摆角控制系统:
由图2可以看出起重机的摆角可以调节定位控制系统保持稳定,因此只考虑定位控制系统控制器的设计。为了使控制器设计方便,需要对其进行模型降阶。利用Matlab提供的最优模型降阶函数opt_app(),结合主导极点法对高阶系统进行降阶,得到降阶后的定位控制系统传递函数为Gx0(s)=K0/s(T0s+1).同绳长控制系统的设计原理,定位控制系统内模二自由度的控制器设计如下:
(13)
(14)
2.2 前馈型内模二自由度控制
由式(3)-(5)可知桥式起重机的定位、摆角和绳长控制系统都是非自衡系统,传统的内模二自由度控制在非自衡系统的应用中是有缺陷的。如果扰动从输入端进入系统,零极点的存在会使系统产生稳态误差甚至发散。为了消除因干扰带来的非零误差,本文在二自由度的基础上引入了前馈控制,在可测扰动信号的不利影响产生前,通过前馈通道抵消扰动对系统输出的影响,使得改进后的内模二自由度控制抗干扰能力大大提高。其结构图如图4所示:
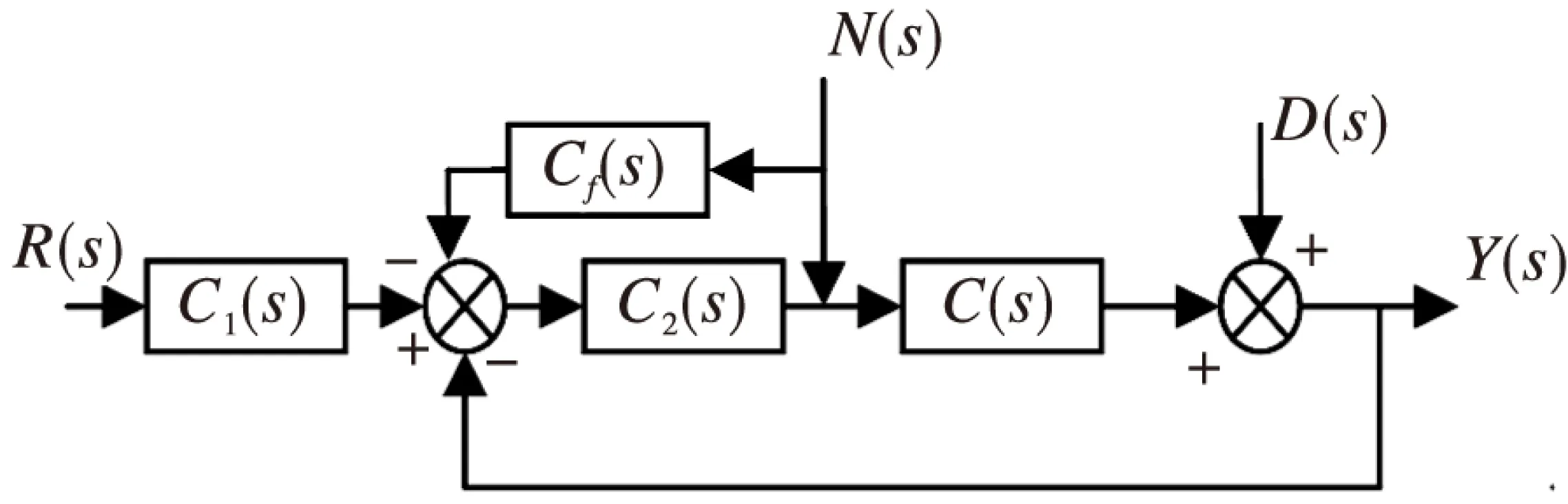
图4 前馈型二自由度控制结构框图
由图4可得:
(15)
(16)
(17)
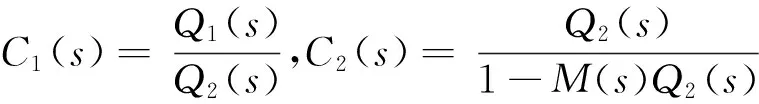
由式(15)-(17)可知,前馈控制器的加入并不影响输入的响应,改进后的内模二自由度不仅具有原来跟随性好、抗干扰能力强的特点,还可以减轻反馈控制的负担,削弱内部干扰的影响,使得响应速度加快。
针对起重机的定位控制系统和绳长控制系统,若要使扰动N(s)对系统的影响为0,需满足:
1+Cf(s)C2(s)=0
(18)
(19)
将式(8)-(10)代入式(19)得到定位、绳长控制系统的前馈控制器:
(20)
(21)
3 仿真研究
为验证所述方法的有效性,进行仿真实验。取参数:M=5 kg,m=10 kg,g=9.8 m/s2,μx=μl=0.2,λ1=0.2,λ2=1.35,λ3=0.01,λ4=0.156.期望的绳长ld=3 m(t≤25 s),ld=2 m(t>25 s);系统的给定输入为r(t)=1(t),扰动输入为dt=0.5(t-20),进行了两组仿真实验,第一组和文献[16]方法进行比较,仿真结果如图5-7所示;第二组将负载质量m=10 kg变为m=15 kg, 扰动输入为dt=0.5(t-20),验证了本文控制器的鲁棒性,仿真曲线如图8-10所示。由图(5)-(7)结果可以看出,本文方法在跟随特性和抗干扰特性方面优于文献[8]方法。在定位控制系统中达到期望位置所用的时间为5 s,负载摆角保持在0.05 rad内;有干扰时,摆角恢复到平衡位置所用时间大大缩短,振荡次数明显减少,对起重机绳长控制系统的影响明显小于文献[16]方法。由图(8)-(10)可以看出当负载的质量由m=10 kg转化为m=15 kg时,小车在8 s内、绳长在5 s内到达期望位置、摆角保持在0.05 rad内;有干扰时也可以快速回到稳定位置,说明系统具有强鲁棒性。
4 结论
本文采用内模二自由度控制方法对解耦后的定位和绳长控制系统进行伺服跟踪控制,利用起重机系统的耦合性达到消摆的目的。前馈控制器对扰动和建模误差进行补偿,减小了静态误差。仿真结果表明该控制器在吊绳长度变化的情况下实现了小车的快速定位和负载的防摆控制,控制器结构简单,鲁棒性强,对外界干扰具有较好的抑制效果。为桥式起重机的定位和防摆控制提供了一种新方法。
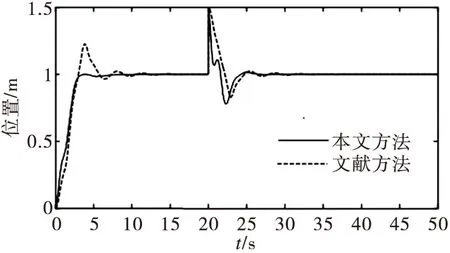
图5 位置仿真曲线
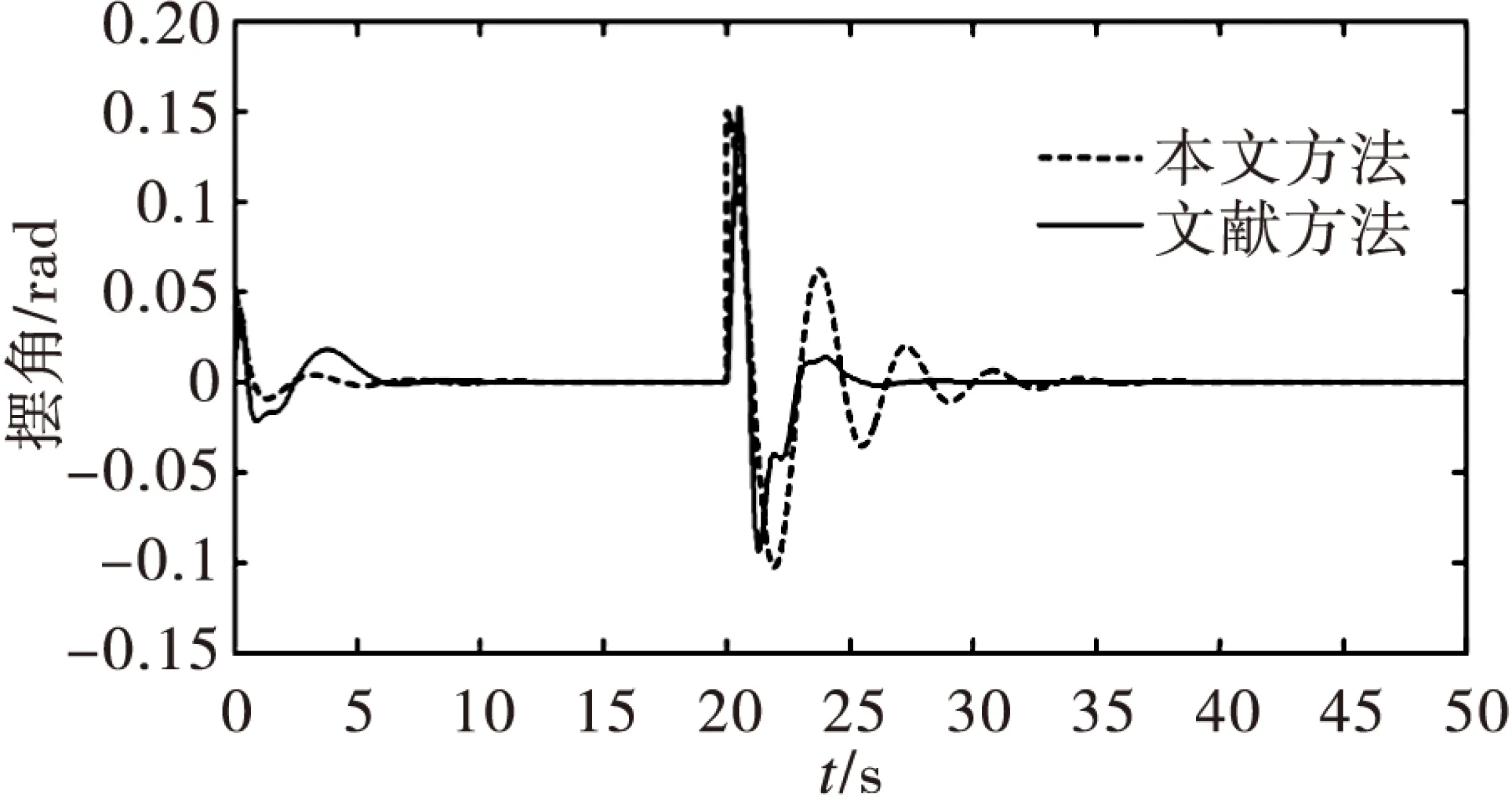
图6 负载摆角仿真曲线
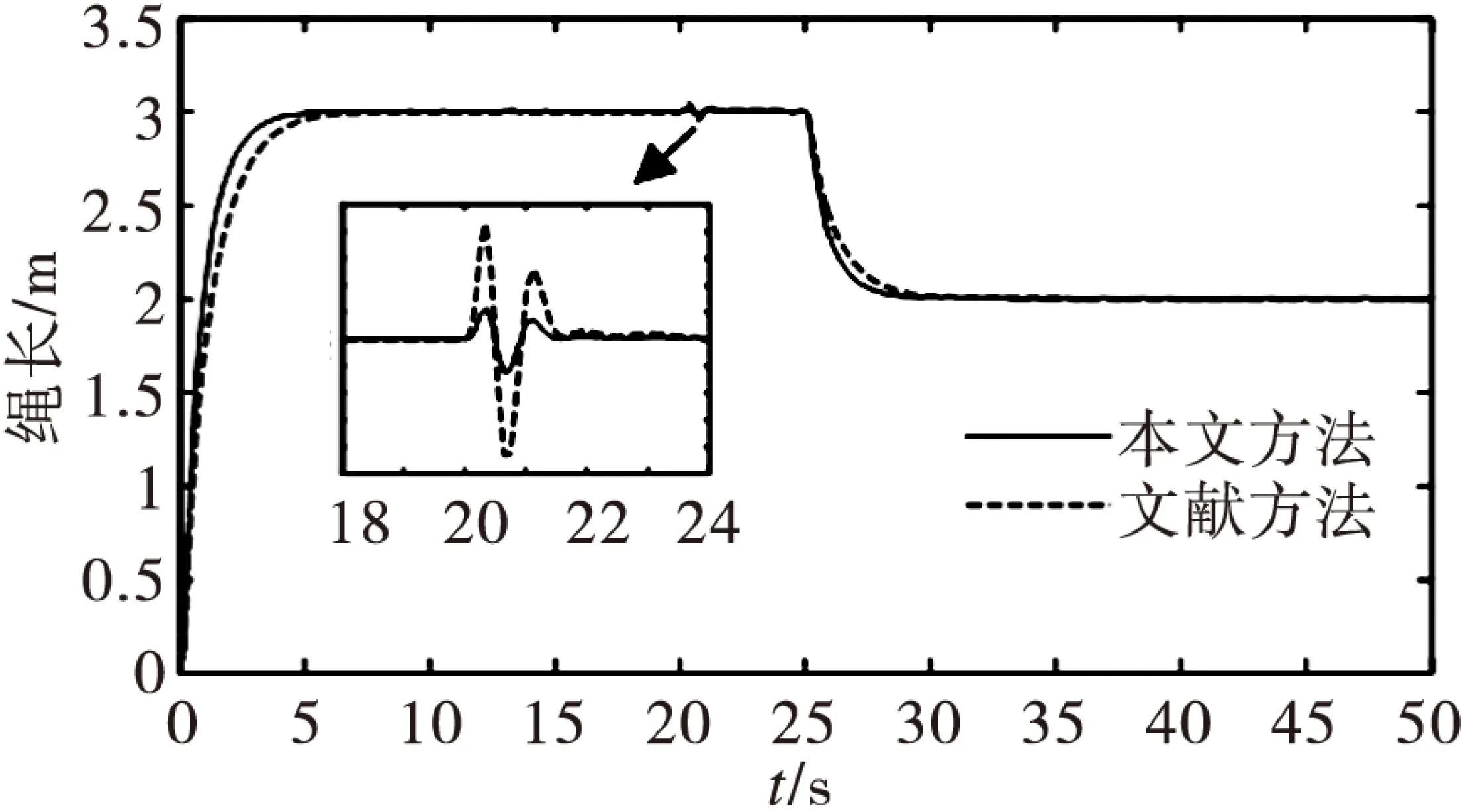
图7 绳长仿真曲线

图8 不同负载质量时位置仿真曲线
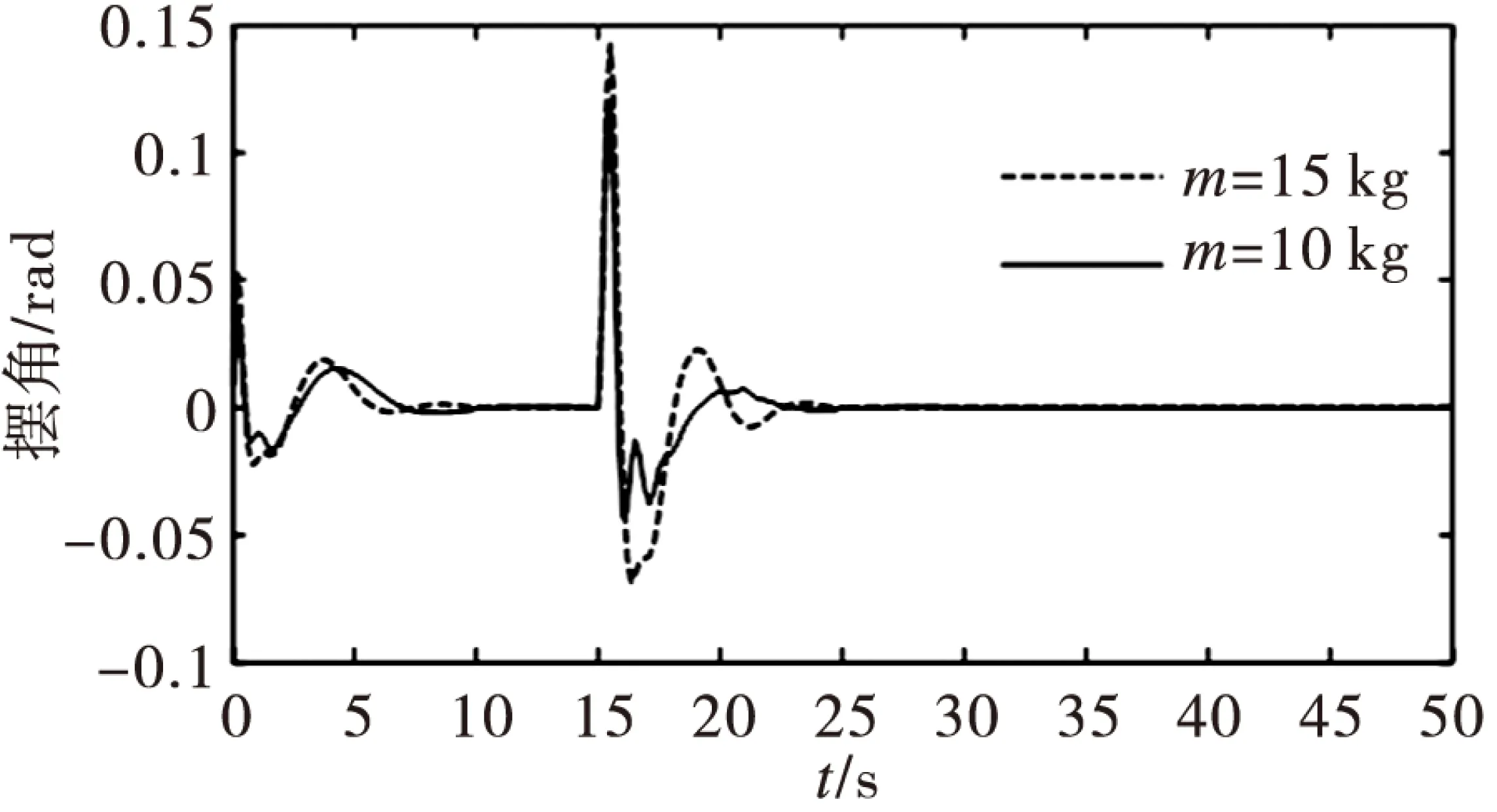
图9 不同负载质量时摆角仿真曲线
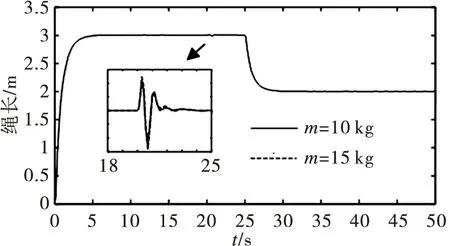
图10 不同负载质量时绳长仿真曲线
[1] 马海峰,丁国富.起重机定位和防摆的变论域模糊控制[J].系统仿真学报,2014,28(2):425-429.
[2] 王晓军,邵惠鹤.基于模糊的桥式起重机的定位和防摆控制研究[J].系统仿真学报,2005(4):936-939.
[3] SMOCZEK J.Fuzzy crane control with sensorless payload deflection feedback for vibration reduction[J].Mechanical Systems and Sial Processing,2014,46(1):70-81.
[4] 谭莹莹,徐为民,徐攀,等.基于动态滑模结构的桥式吊车防摇定位控制器设计[J].控制工程,2013(S1):117-121.
[5] LEE S H,PARK J B,CHOI Y H.Finite time control of nonlinear underactuated systems using terminal sliding surface[C]∥Industrial Electronics,2009.ISIE 2009.IEEE International Symposium on.IEEE,2009:626-631.
[6] PISANO A,SCODINA S,USAI E.Load swing suppression in the 3-dimensional overhead crane via second-order sliding-modes[C]∥Variable Structure Systems (VSS),2010 11th International Workshop on.IEEE,2010:452-457.
[7] XU W M,LIU B,CHU J X,et al.An anti-swing and positioning controller for overhead cranes based on multi-sliding mode method[J].Advanced Materials Research,2012,468:328-334.
[8] 何航,宛西原,胡宇.起重机模糊神经网络防摇摆控制仿真研究[J].自动化与仪器仪表,2014(1):10-14.
[9] SUTIKNO J P,AZIZ B A,YEE C S,et al.A New Tuning Method for Two-Degree-of-Freedom Internal Model Control under Parametric Uncertainty[J].2013,21(9):1030-1037.
[10] 胡明慧,邵惠鹤.基于灵敏度函数的二自由度控制系统设计与应用[J].上海交通大学学报,2007(11):1792-1795.
[11] 夏运霞,包启亮,李锦英.光电跟踪系统视轴稳定的鲁棒内模控制器设计[J].控制与决策,2013(7):1117-1120.
[12] 赵曜.改进型内模控制系统的稳定性与鲁棒跟踪条件[J].控制与决策,2007(4):477-480.
[13] VILANOVA R,ALFARO V M,ARRIEAT O.Simple robust autotuning rules for 2-DoF PI controllers[J].Isa Transactions,2012,51(1):30-41.
[14] KAYA I.Two-degree-of-freedom IMC structure and controller design for integrating processes based on gain and phase-margin specifications[J].Control Theory and Applications,IEE Proceedings-.IET,2014,151(4):481-487.
[15] ZHOU Y.The variable frequency speed control system based on the modified two-degree-freedom internal model control and its robustness analysis[C]∥Control and Decision Conference (CCDC),2010 Chinese.IEEE,2010:2719-2724.
[16] 王克琦.桥式起重机的定位和防摆控制研究[J].系统仿真学报,2007,19(8):1799-1802.
Research of Two-Degree-of-Freedom IMC Anti-swing Control for Bridge Crane
WANG Xiao-jing,CHEN Zhi-mei,SHAO Xue-juan
(Department of Electronic Information Engineering,Taiyuan University of Science and Technology,Taiyuan 030024,China)
A new positioning and anti-swing control scheme of two-degree-of-freedom internal model control (IMC)is proposed.The controller of bridge crane is changed to two servo-tracking subsystems with card position and cord length.Meanwhile,the angle of load should be kept stable by making use of the coupling of modules.The designed controller according to IMC theory can bring a process to keep good characteristics of required tracking and disturbance,as well as robustness.So the swing of heavy load can be restrained when the crane trolley and variable rope reach the expected position.Theoretical analysis and simulation results show the validity of this control method.
bridge cranes,coupling,anti-swing control,internal model control,two-degree-of-freedom
2015-09-30
山西省自然科学基金(2014011020-2,2014011020-1)
王小静(1991-),女,硕士研究生,主要研究方向为起重机定位防摆控制;通信作者:陈志梅教授,E-mail:zhimeichen400@163.com
1673-2057(2016)05-0337-05
TP273
A
10.3969/j.issn.1673-2057.2016.04.001

