一种求解二次模型信赖域子问题的Admas4隐式算法

王英慧，王希云

(太原科技大学 应用科学学院，太原 030024)



一种求解二次模型信赖域子问题的Admas4隐式算法

王英慧，王希云

(太原科技大学 应用科学学院，太原 030024)

基于信赖域子问题最优曲线的微分方程模型，在Hessian矩阵正定及步长固定的前提下，采用求解微分方程的Admas4隐式公式构造了一条折线，称Admas4隐式折线，用其代替最优曲线，提出求解子问题的新算法—Admas4隐式算法。数值结果表明Admas4隐式算法比R-K4算法效果好。

微分方程模型；信赖域子问题；Adams4隐式算法

在非线性优化中，信赖域方法不仅具有很好的可靠性和强适性，而且具有较强的收敛性。因而，自其出现起就受到高度重视，成为热点。信赖域方法实现的关键是每步迭代时要求解一个二次模型信赖域子问题，其形式如下：

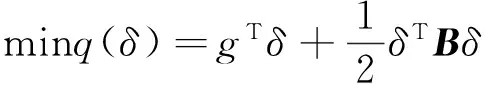
(1)

(1)中的各个参数表示的含义分别是：g∈Rn：目标函数在当前点的梯度，B∈Rn×n：目标函数在当前点处的Hessian矩阵或者它的近似矩阵，△∈R：信赖域半径，δ∈Rn：要求的变量。当△发生变化时，子问题(1)的解δ*在空间形成一条曲线——最优曲线。

针对最优曲线的参数方程，在Hessian矩阵正定的前提下，有如下微分方程模型[1]：

(2)

对于子问题(1)的求解，目前提出的方法主要有单折线法、双折线法、切线单折线法。后来李亮提出最优曲线的微分方程模型之后，基于此微分方程模型，先后提出了解决信赖域子问题的隐式分段折线法、分段切线法、平均欧拉算法及休恩算法[1-4]。后来又提出了解二次模型子问题的R-K4算法。该算法主要是利用解微分方程模型的R-K4公式，构造一条R-K4折线，进而用此折线代替最优曲线来求解子问题(1)的解。为进一步提高数值计算结果的精度，本文结合求解微分方程的较高阶的Admas4隐式公式[5]，构造了Admas4折线代替最优曲线来求解子问题(1)，并将数值结果与R-K4方法做了比较。

1 Adams4隐式折线的构造

Admas4隐式公式如下：

(n=2,3,4,…)

(3)

其中：

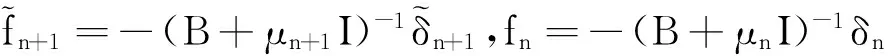
μn=μ0+nh.具体构造如下：

第一步：从初始点P0(μ0,δ0)开始，其中μ0=0，δ0=-B-1g.选取步长，用公式:

(4)

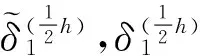
第二步：由常用的四阶龙格-库塔公式:

若记：f01=-(B+μ0I)-1δ0,

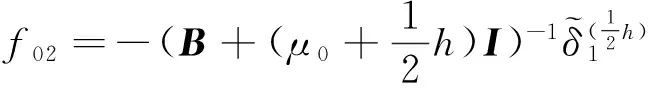
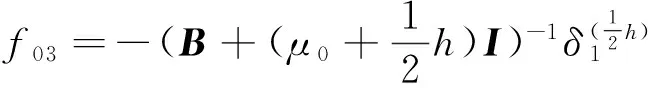
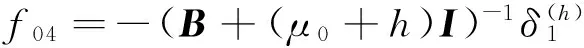
则：

(5)

计算出δ1，得出下一个节点P1(μ1,δ1)，其中μ1=μ0+h.同理计算出δ2，得到节点P2(μ2,δ2).

(6)

其中μ0=0，μn=μn-1+h,n=1,2,3,…,N.

2 对步长h的限定

为了使构造的折线满足引理6.4.1[6]，则步长需要满足下式:

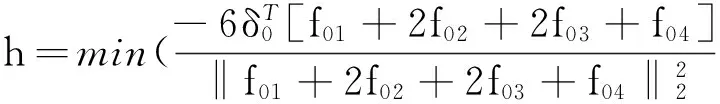
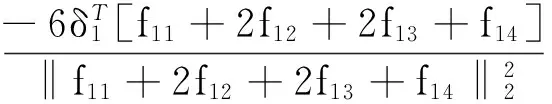
(7)

3 Admas4隐式折线路径的性质定理

定理1 设B对称正定，且当n=0,1时有:

gT[fn1+2fn2+2fn3+fn4]+

(8)

n=2,3,…时，有：

(9)

则δ(τ)满足：

(1)‖δ(τ)‖2关于τ为单调减函数。

(2)q[δ(τ)]关于τ为单调增函数。

证明：(1)当τ∈[μ0,μ1]，即τ∈[0,h0]时:

则：

由式(7)得：

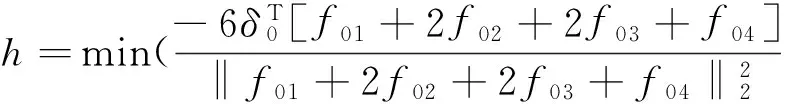
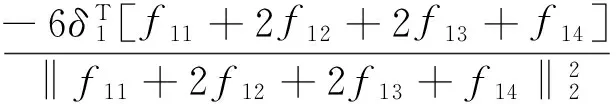
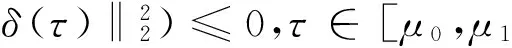
因此，‖δ(τ)‖2在区间[μ0,μ1]，[μ1,μ2]上为单调减函数。

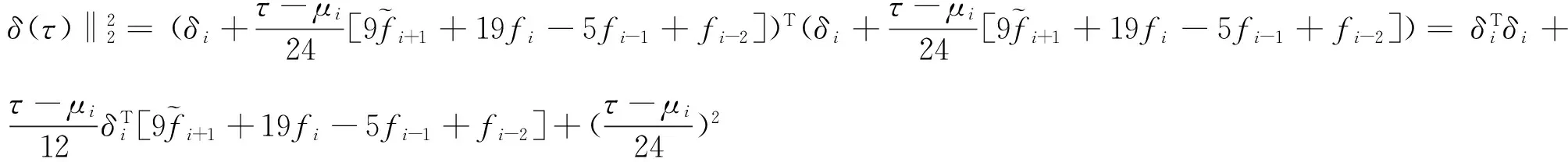
则：

由式(7)得：

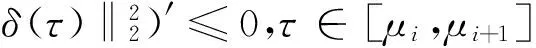
因此‖δ(τ)‖2在区间[μi,μi+1],i=1,2,3，…,N-1上为单调减函数。

(2)当τ∈[μ0,μ1]，即τ∈[0,h0]时:

则：

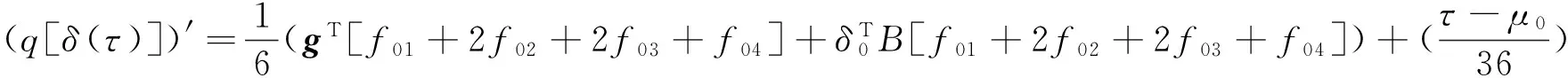
由已知条件式(8)：

gT[f01+2f02+2f03+f04]+

得：(q[δ(τ)])′≥0,τ∈[μ0,μ1].

同上，可以证明(q[δ(τ)])′≥0,τ∈[μ1,μ2].

所以q[δ(τ)]在区间[μ0,μ1]，[μ1,μ2]上关于τ为单调增函数。

对∀τ∈[μi,μi+1]，即:

(τ-μi)∈(0,hi),i=1,2,3,…,N-1时：

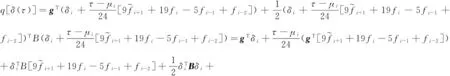
由已知条件(9)：

可得：(q[δ(τ)])′≥0,τ∈[μi,μi+1].

所以：q[δ(τ)]在区间[μi,μi+1]，i=0,1,2,3,…,N-1上关于τ为单调增函数。(证毕)。

4 算法描述

通过上面的讨论，下面给出Admas4隐式折线算法的具体步骤：

步0 给定梯度g，正定矩阵B，信赖域半径△.令n∶=0.

步1 令δ0=-B-1g.

步2 如果△≥‖δ0‖2，则取δ*=δ0，停止计算。否则，令n∶=n+1，转步3.

步3 选取适当步长，令:

其中μ0=0.令:

如果△≥‖δ1‖2，则取：

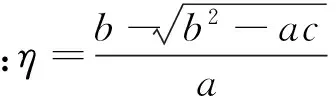
步4 令:

如果△≥‖δ2‖2，则取:

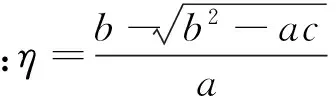
步5 根据公式:

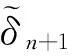
根据公式：

计算δn+1，转步6.

步6 如果△≥‖δn+1‖2，则取:

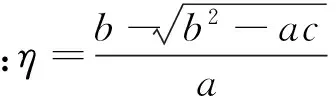
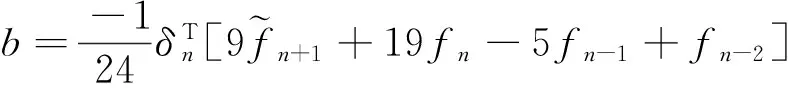
停止计算，否则令n∶=n+1，转步5.

5 Admas4隐式折线算法的适定性

由定理1可知下列结论成立：

定理2 设B对称正定，在Admas4隐式算法中，对任意给定的信赖域半径△<‖B-1g‖2，则存在自然数N使得‖δN‖2≤△.

定理1和定理2说明对任意给定的信赖域半径△，在Admas4隐式折线δ(τ)上的近似解存在且唯一。并且用Admas4隐式算法求信赖域子问题(2)的最优解时，最优解δ*在信赖域边界上取得。

6 数值实验

对于附录中给定的测试函数1和测试函数2的信赖域子问题(1)，取h=0.1，选取不同的信赖域半径△，然后将Admas4隐式算法利用MATLAB进行了数值实验。并且用该算法求得的测试函数在近似最优解的函数值与R-K4方法进行比较，数值结果分别列在表1和表2中。

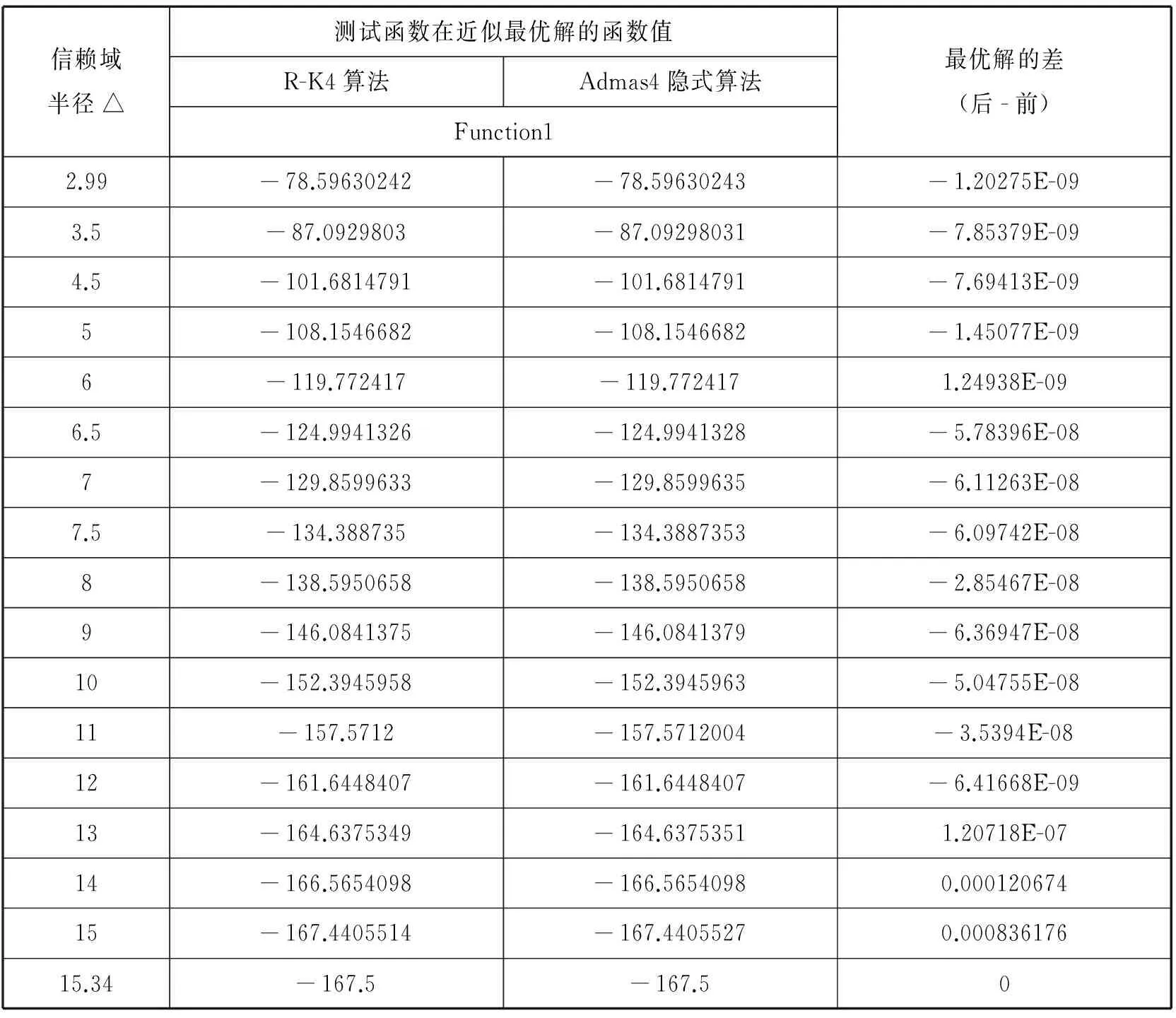
表1 测试函数1的数值结果

从表1和表2的数值结果可以看出，本论文所提出的Admas4隐式算法是有效且可行的。对于测试函数1和测试函数2，当信赖域半径△<‖B-1g‖2时，除了信赖域半径在‖B-1g‖2附近的情况，Admas4隐式算法求得的测试函数在近似最优解的函数值比R-K4效果要好；当信赖域半径△≥‖B-1g‖2时，则Admas4隐式算法与R-K4算法所求得的测试函数在近似最优解的函数值相同。因此，本论文所构造的Admas4隐式算法比R-K4算法更好地近似了最优曲线，而且Admas4隐式算法也是一个很好的求解信赖域子问题(1)的折线法。

对于测试函数1，‖B-1g‖2=15.34.对于测试函数2，‖B-1g‖2=10.01.

附录：测试函数

Function1：

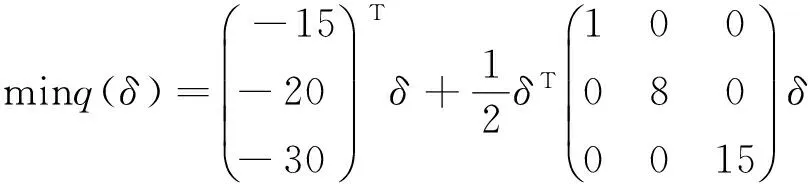
s.t.‖δ‖2≤△.

Function2：

s.t.‖δ‖2≤△

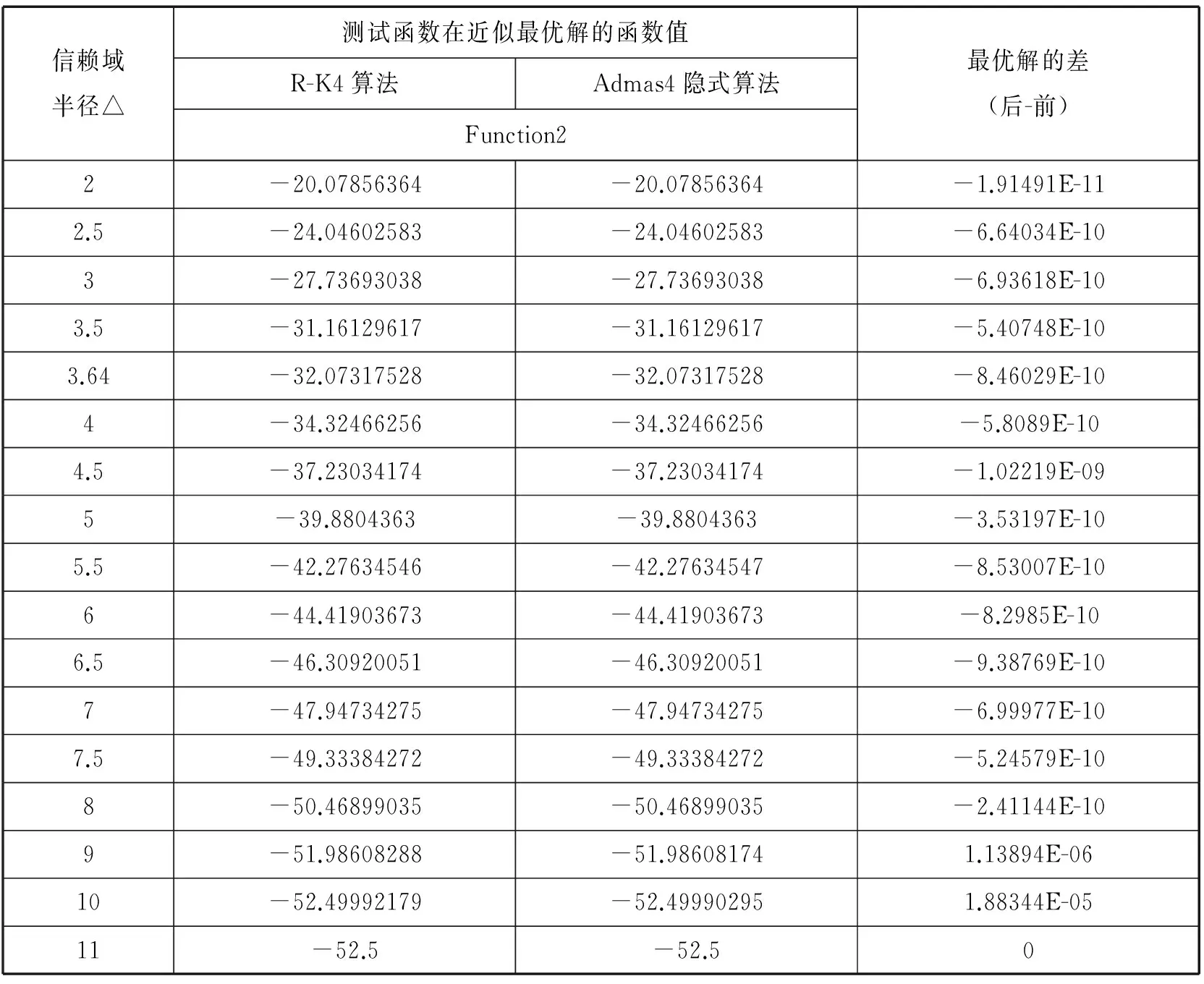
表2 测试函数2的数值结果

[1] 王希云，李亮，于海波.解决信赖域子问题的隐式分段折线算法[J].应用数学和力学，2014，35(6)：610-619.

[2] 王希云，李亮，张雅琦，等.一种求解二次函数模型信赖域子问题的分段切线法[J].应用数学，2015，28(1)：26-32.

[3] 朱帅，李亮，王希云.一种求解二次模型信赖域子问题的新算法[J].西南民族大学学报，2014，40(1)：91-96.

[4] 李亮，王希云，张雅琦，等.一种求解二次模型信赖域子问题的休恩算法[J].太原科技大学学报，2014，35(2)：151-155.

[5] 林成森.数值计算方法[M].北京：科学出版社，2005.

[6] 李董辉，童晓娇，万中.数值最优化算法与理论[M].北京：科学出版社，2010.

An implied Adams4′s Algorithm for Solving Trust-region Subproblems with Quadratic Model

WANG Ying-hui，WANG Xi-yun

(School of Applied Science，Taiyuan University of Science and Technology，Taiyuan 030024，China)

In the premise of Hessian matrix as a positive definite matrix and fixed step，a broken line is constructed by implied Adams4′s method according to the differential equation model，which is defined as Admas4 implicit broken line instead of the optimal curve.Through the comparison with the R-K4 method，the results indicate that Adams4 implicit algorithm has obvious advantage over the R-K4 method.

differential equation model，trust-region subproblems，implied Adams4′s method

2015-09-23

山西省高校‘131’项目基金

王英慧(1987-)女，硕士研究生，主要研究方向为最优化理论与应用。

1673-2057(2016)05-0406-06

O221

A

10.3969/j.issn.1673-2057.2016.04.014