沥青路面三维纹理分形维数及其抗滑性能

钱振东，薛永超，张令刚



沥青路面三维纹理分形维数及其抗滑性能

钱振东，薛永超，张令刚

(东南大学智能运输系统研究中心，江苏南京，210096)

研究沥青路面抗滑性能与三维纹理分形维数的关系。成型4种SMA沥青混凝土车辙板，采用数字图像处理技术重构车辙板表面三维纹理模型，实测车辙板表面构造深度检验重构的三维纹理模型的有效性，通过差分盒维数法计算三维纹理模型的分形维数，研究分形维数与抗滑性能的关系。研究结果表明：重构的三维纹理模型在纹理构造特征上以较高精度恢复原沥青路面的表面形貌，计算的分形维数与实测的摆值、构造深度具有良好的相关性，可以较好地表征沥青路面的抗滑性能；构造深度随着分形维数的增加而减小，摆值随着分形维数的增加先减小后增加。

沥青路面；抗滑性能；三维纹理模型；分形维数

国内外大量研究表明，沥青路面的抗滑性能与路面表面纹理具有紧密联系，路面表面纹理可以较好地反映沥青路面的抗滑性能[1−4]。目前，人们对于沥青路面表面纹理特性的研究大多采用二维断面轮廓，但实际沥青路面表面纹理是三维的，二维轮廓断面仅能反映片面的形貌特征。数字图像处理技术可以通过物体表面的二维灰度图像重构物体表面的三维形貌[5−6]。王端宜等[7−9]将数字图像处理技术引入沥青路面表面构造深度测量，通过对沥青路面二维灰度图像像素分析，恢复路面三维纹理模型，并提出计算沥青路面构造深度的积分方法，对研究沥青路面的抗滑性能具有重要意义。对沥青路面表面纹理构造的传统描述参数一般包括轮廓参数(轮廓算术平均偏差和轮廓均方根偏差)、统计分布参数、形状分布参数(偏态系数和峰态系数)、支承面积曲线等统计学参数，但沥青路面表面纹理变化是一种非平稳的随机过程，传统描述参数随着量测尺寸和区间的变化表现出不稳定性[10−11]。因此，对沥青路面表面纹理特性的研究，需要确定合适、稳定的描述参数。沥青路面表面三维纹理模型的分形维数可以较好地表征其所具有复杂结构的数量以及复杂结构的精细程度，是沥青路面分形特性的主要参数，分形维数越大，则沥青路面表面形貌越复杂，细节越丰富，因此，考虑将沥青路面的抗滑性能与其分形维数建立关系。本文作者成型4种不同级配类型的沥青混凝土车辙板，应用数字图像处理技术对车辙板表面三维纹理模型进行重构，在确定重构模型有效性的基础上，计算模型的分形维数，并与沥青路面抗滑性能建立关系。

1 沥青路面表面三维纹理模型重构

制备4种级配类型的沥青混凝土车辙板，对车辙板的表面纹理进行数字图像获取以及预处理，根据处理后的图像重构三维纹理模型。

1.1 沥青混凝土车辙板制备

SMA沥青混凝土具有良好的表面纹理构造，从图像处理角度，骨架结构的路面表面纹理更利于图像识别。选取SMA16，SMA13，SMA10和SMA5这4种典型级配类型，采用SBS改性沥青和玄武岩集料，其基本性能参数见表1及表2，分别成型4组车辙板试件，每组3块。试件成型采用轮碾法，其长×宽×高为300 mm×300 mm×50 mm，试验参照JTG E20—2011中的T0703规程进行。4种SMA沥青混凝土的设计级配及其最佳油石比(即沥青与集料的质量比)如表3所示。

表1 SBS改性沥青的性能参数

表2 玄武岩集料的性能参数

1.2 数字图像提取及预处理

采用数码相机及固定支架等设备。数码相机拍摄车辙板表面时会发生漫反射，图像上每个像素灰度代表路面对应点的凹凸状况。图像提取的主要步骤包括：调节相机高度和角度，使之镜头距车辙板试件表面 20 cm，且与车辙板试件表面垂直；调整光照角度，并使ISO、光圈、快门等相机参数为最佳组合；拍摄车辙板试件的上表面，并存储为RAW格式。

数字图像不可避免的存在噪点，须进行降噪处理。通过MATLAB对所拍图像使用中值滤波算法进行降噪处理。

1.3 三维纹理模型重构

由于MATLAB对图像处理的大小有限，图像尺寸越大，处理速度越慢，且可能发生溢出错误，故将降噪后的车辙板表面数字图像进一步切割为150像素×150像素进行分析。采用MATLAB将切割后的图像转换为灰度图像，通过MATLAB读取灰度图像的坐标和灰度，得到该图像的像素矩阵，根据像素矩阵重构车辙板表面的三维纹理模型，如图1所示。

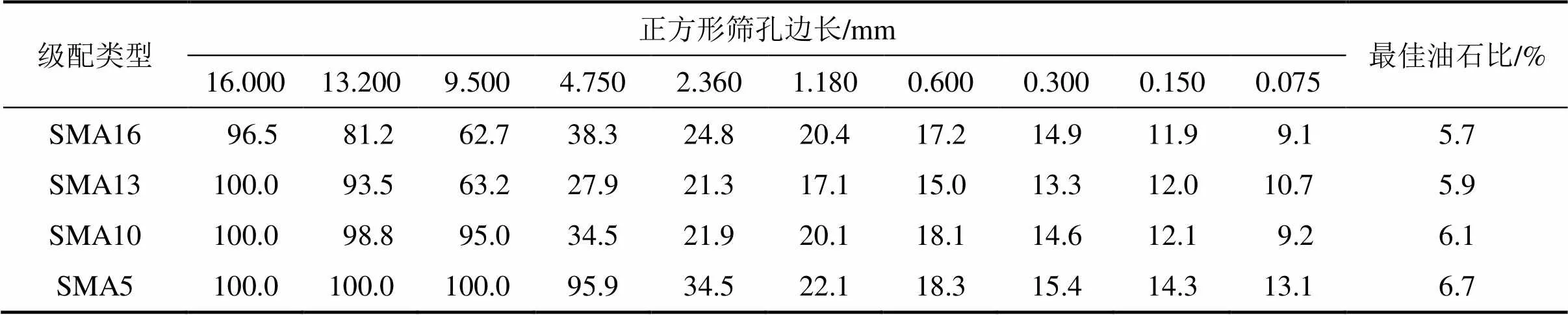
表3 设计级配及其最佳油石比

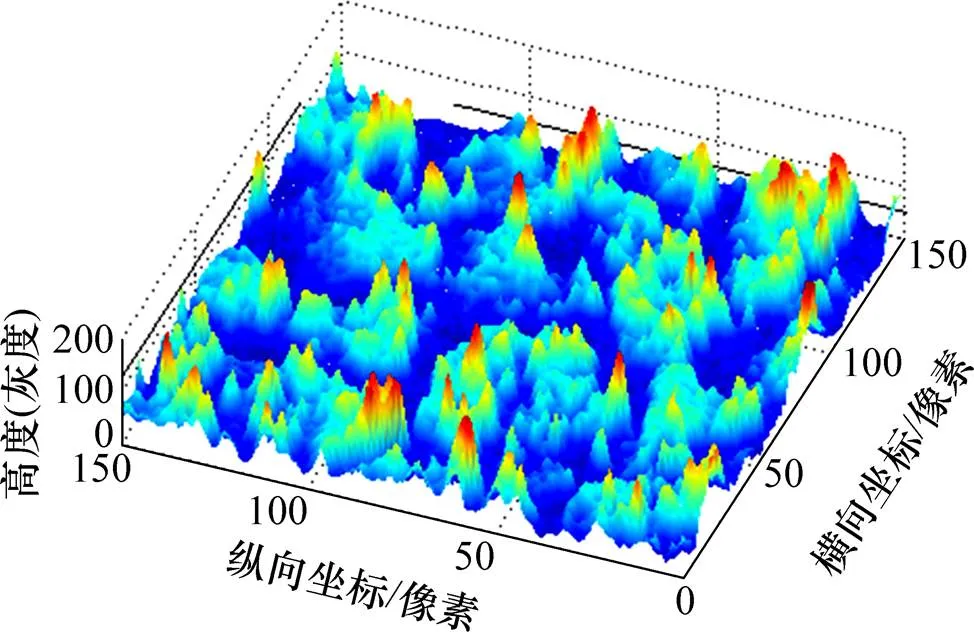
图1 沥青路面表面三维纹理模型

从图1可以看出：重构的三维纹理模型具有与车辙板表面类似的纹理构造特征，包括显著的凸峰与 沟壑。

2 三维纹理模型有效性检验

通过试验测出沥青混凝土车辙板表面的真实构造深度以及摆值，并与用灰度作为基本单位计算的构造深度进行对比分析，以验证三维纹理模型的有效性。

2.1 抗滑性能参数实测

用于描述沥青路面表面抗滑性能的参数主要有构造深度D和摩擦摆值BP。用手工铺砂法测定四组车辙板的构造深度，以反映路表的宏观纹理；用摆式仪法测定4组车辙板的摩擦摆值，以反映在宏观纹理和微观纹理共同影响下路表的综合抗滑性[12]。对4组车辙板进行编号(共12组)，试验结果如表4所示。

2.2 三维纹理模型构造深度计算

铺砂法中构造深度为所用细砂体积与铺砂圆形面积的比值，运用到三维纹理模型中纹理曲面(，)与铺砂平面0围成的空间体积与铺砂面积的比值，其中由有限个离散的数据点构成的纹理曲面(，)的解析式为

式中：为沥青路面表面纹理构造的高度；为三维纹理模型的横向坐标；为三维纹理模型的纵向坐标。将纹理曲面(，)与铺砂平面0围成的空间看作由一个个微小的长方体构成，每个长方体对应着1个像素点。由于铺砂测量中，存在部分区域是没有被细砂覆盖的，这部分区域的高度较大，在计算空间体积时需要将这部分区域删掉，即留下高度顶点为铺砂平面0的长方体。留下的长方体的高度H表达式为

式中：为铺砂区域；为圆形铺砂区域的直径。

将式(3)中所有与高度有关的参数都用相应的灰度来代替，则计算的T实际上是一种用灰度作为基本单位的构造深度，具体的计算通过MATLAB编写程序完成，步骤如下。

1) 对铺砂后的车辙板进行与铺砂前的车辙板一样的图像处理，直至转换为灰度图像，采用大津法获取阈值[13−14]，得到铺砂图的二值图，如图2(a)所示。大津法是一种阈值确定方法，该方法具有自适应性，它根据图像灰度的分布特性，将其分割成背景与目标2部分。计算这2部分的类间方差，其值越大，表明背景与目标的差异越大[15]。

2) 提取二值图的边缘图像，将二值图、边缘图与铺砂原图对比，反复调整二值图的阈值，直至三者的轮廓互相匹配为止。边缘图与铺砂原图分别如图2(b) 与2(c)所示。

3) 当三者的轮廓相匹配时，计算此时露出铺砂平面的面积与总面积的比值，根据此比值确定铺砂前的三维纹理模型的铺砂平面位置，如图2(d)所示。

表4 抗滑性能参数实测结果

*:BP为摆式仪法中的摩擦摆值；数字1~12为车辙板编号。

(a) 二值图；(b) 边缘图；(c)铺砂原图；(d) 三维纹理模型里的铺砂平面

4) 根据铺砂平面的位置计算铺砂平面的灰度，并计算纹理曲面不同位置的灰度及像素点的个数，将灰度作为式(3)中相应的高度代入式(3)，计算最后用灰度作为基本单位表示的构造深度。

2.3 有效性检验

选取每组车辙板中的前2块，对它们的实测构造深度与用灰度表示的构造深度进行回归分析，分析结果如图3所示。

从图3可以看出：用灰度表示的构造深度与实测构造深度具有很好的一次函数关系，表明灰度只是构造深度的一种等比例放大表示，这与实际情况相符，进而说明重建的三维纹理模型在纹理构造特征上较好地恢复了原沥青路面的表面形貌，而且精度较高。

运用图3中的一次函数关系，将用灰度表示的构造深度换成用高度表示的构造深度，并与每组车辙板中第3块的实测构造深度进行比较，如图4所示。从图4可见：构造深度计算值与实测值相差很小，误差在允许范围之内，再次证明重建的三维纹理模型较好地表征了原沥青路面表面形貌的纹理构造特征，所构建的三维纹理模型是有效的，可用于后面的分形性质计算。

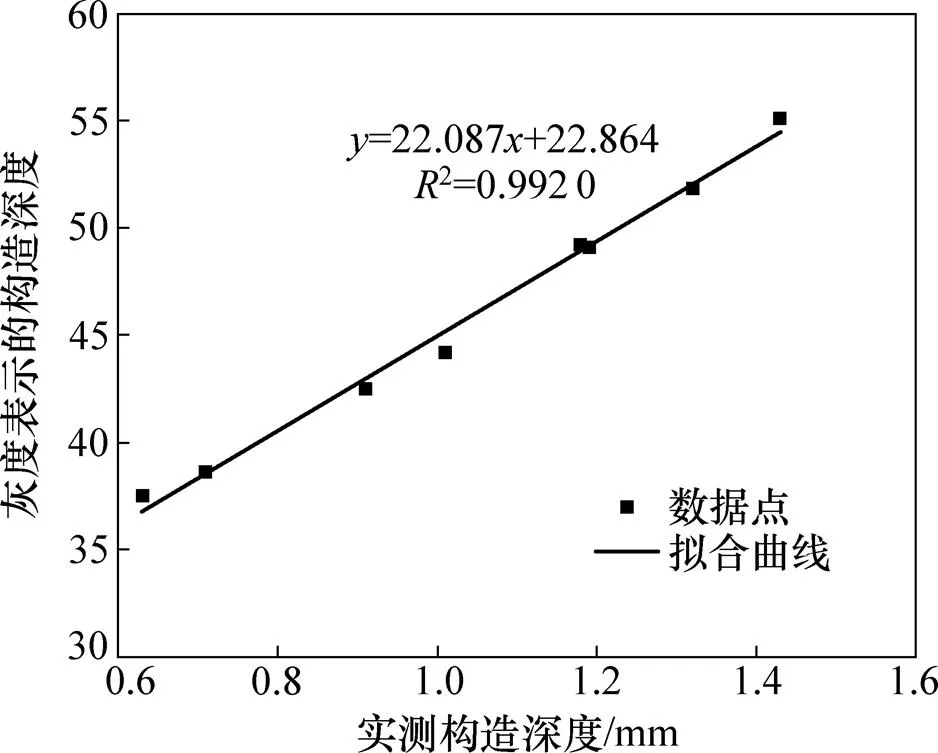
图3 回归分析结果

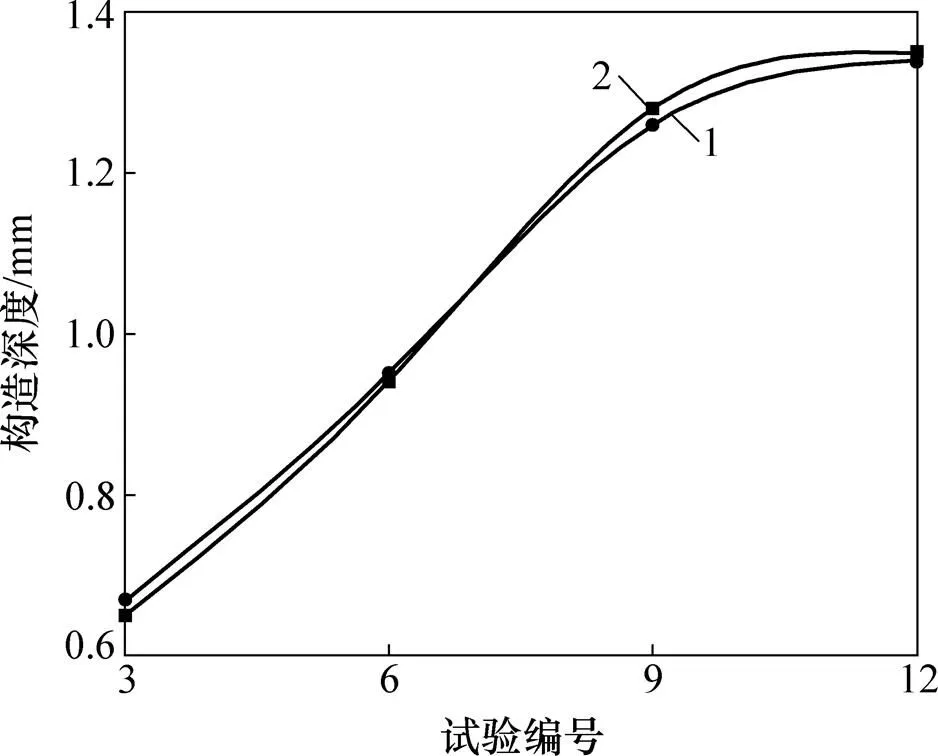
1—实测构造深度；2—计算构造深度。

3 沥青路面抗滑性能分析

3.1 分形维数计算方法优选

采用傅里叶反变换法编写MATLAB程序，模拟不同分形维数的分数布朗运动曲面[16]，分别应用变分法、功率谱法和差分盒维数法计算曲面的分形维 数[17−19]，结果如表5所示。

从表5可见：变分法与功率谱法计算布朗运动曲面时稳定性较差，对分形维数变化过分敏感；差分盒维数法计算值与理论值接近，且具有较好的稳定性，算法简单明了，便于编写程序。为此，本文选取差分盒维数法计算沥青路面表面三维纹理的分形参数。

3.2 分形维数计算

差分盒维数法计算过程为：将垂直投影为×的三维空间曲面在投影得到的平面上分割成×的网格(/2≥≥2，其中，为三维空间曲面垂直投影的边长，为切割的网格边长，且为整数)；令=/，对于三维空间曲面，轴与轴表示平面位置，轴表示高度(灰度)，−平面被分割成许多×的网格，在每个网格上，是一系列××的盒子。其中，为盒子高度(灰度)，令=/。

设三维空间曲面高度在第(，)网格中最小值落在第个盒子中，最大值落在第个盒子中，则有

其中：r(，)为覆盖第(，)网格曲面中的盒子数。覆盖整个曲面需要的盒子总数()为

则根据定义分形维数为[19]

针对不同的，利用最小二乘法对数据点(ln1/，ln())进行线性拟合，可求得直线方程：

结合式(6)，式(7)中斜率即为分形维数。

将前面得到的12块车辙板表面三维纹理模型网格化，应用MATLAB编程进行分形维数的计算，所有车辙板的分形维数见表6。以SMA5类型的第1块为例，得到分析维数拟合曲线如图5所示。

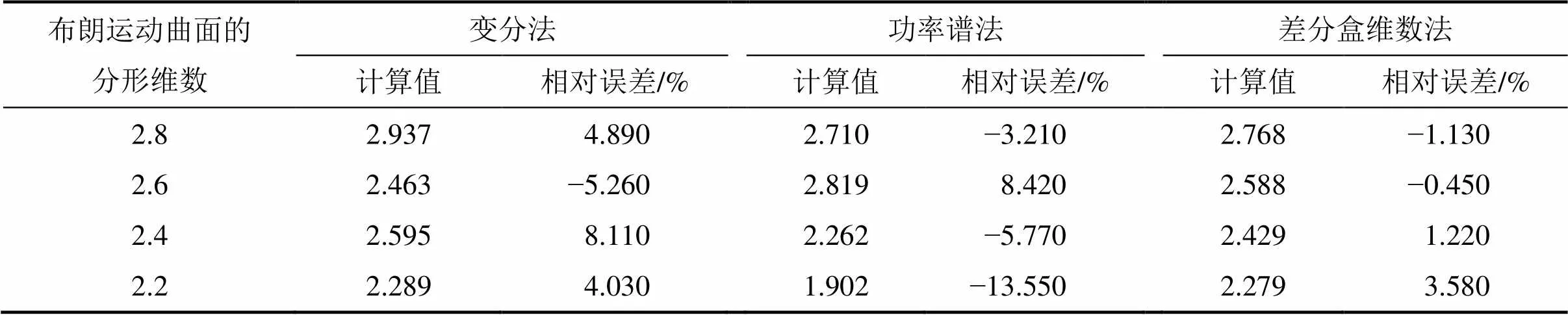
表5 分形维数计算结果

表6 分形维数

*: 数字1~12为车辙板编号。

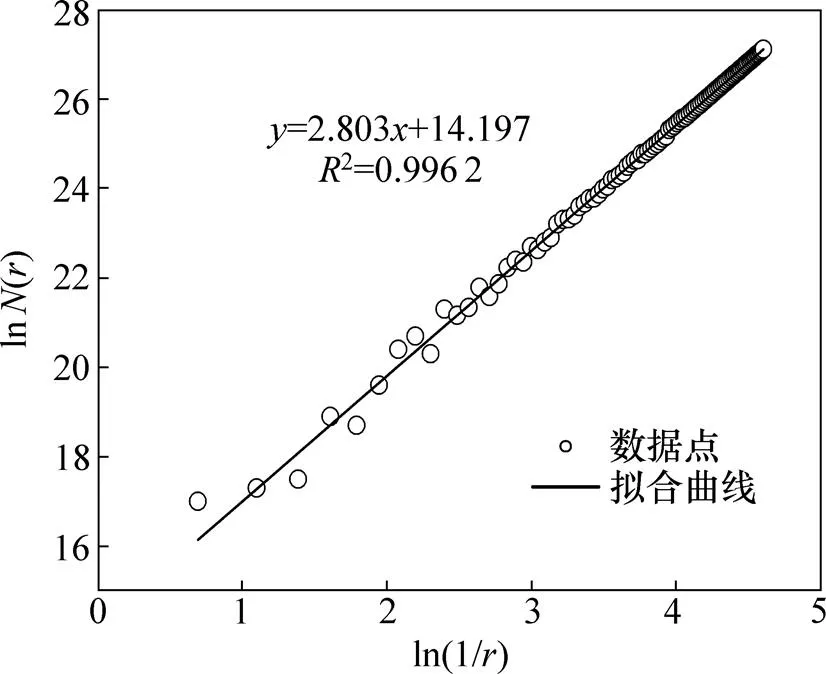
图5 分形维数拟合曲线

从图5和表6可以看出：使用差分盒维数法拟合的直线具有很好的相关性，车辙板试件表面三维纹理在图中的尺度范围内具有很好的分形特征，求得的分形维数误差均较小，并且随着集料最大粒径的增加，分形维数表现出变小的趋势，这与实际情况相一致；随着最大粒径增大，混凝土整体“变粗”，表面形貌则表现出凹凸峰的高度与间距变大，构造的复杂程度降低。

3.3 三维纹理分形维数与抗滑性能的关系

为了研究三维纹理分形维数与抗滑性能的关系，对表2中实测的构造深度和摆值与表4中的三维纹理分形维数进行回归分析，分析结果如图6所示。

从图6(a)可以看出：构造深度随着分形维数的增大而减小，这是因为分形维数表征的是沥青路面表面形貌的复杂性和自相似性；当分形维数较小时，沥青路面表面纹理构造的复杂程度较低，具体表现为凹凸峰的高度与间距较大，即构造深度较大；当分形维数较大时，沥青路面表面纹理构造较丰富，凹凸峰的密度较大，即构造深度较小。

从图6(b)可以看出：分形维数与摆值并非具有完全单调的递增或递减关系，在最低点的左侧，摆值随着分形维数的增大而减小；在最低点的右侧，摆值随着分形维数的增大而增大。这是因为摆值是沥青路面表面宏观纹理与微观纹理综合作用的结果，当分形维数较小时，集料最大粒径较大，摆值主要受最大粒径影响；随着分形维数增加，集料最大粒径减小，摆值减小；当分形维数较大时，集料最大粒径较小，摆值主要受集料表面微观纹理影响，随着分形维数增加，集料表面纹理更加精细复杂，摆值增大。

从图6可以发现分形维数与构造深度具有相关性较好的二次函数关系，与摆值具有相关性较好的三次函数关系，说明根据图中拟合的公式，沥青路面表面三维纹理计算的分形维数可以较高精度地表征沥青路面表面的抗滑性能，而且作为一种能同时表征构造深度与摆值的参数，能避免根据某单一参数设计出“粗而不糙”的路面；同时，分形维数的测定具有简单方便、再现性强以及对路面无损伤等特点，可以应用于沥青路面抗滑性能的实时监测。

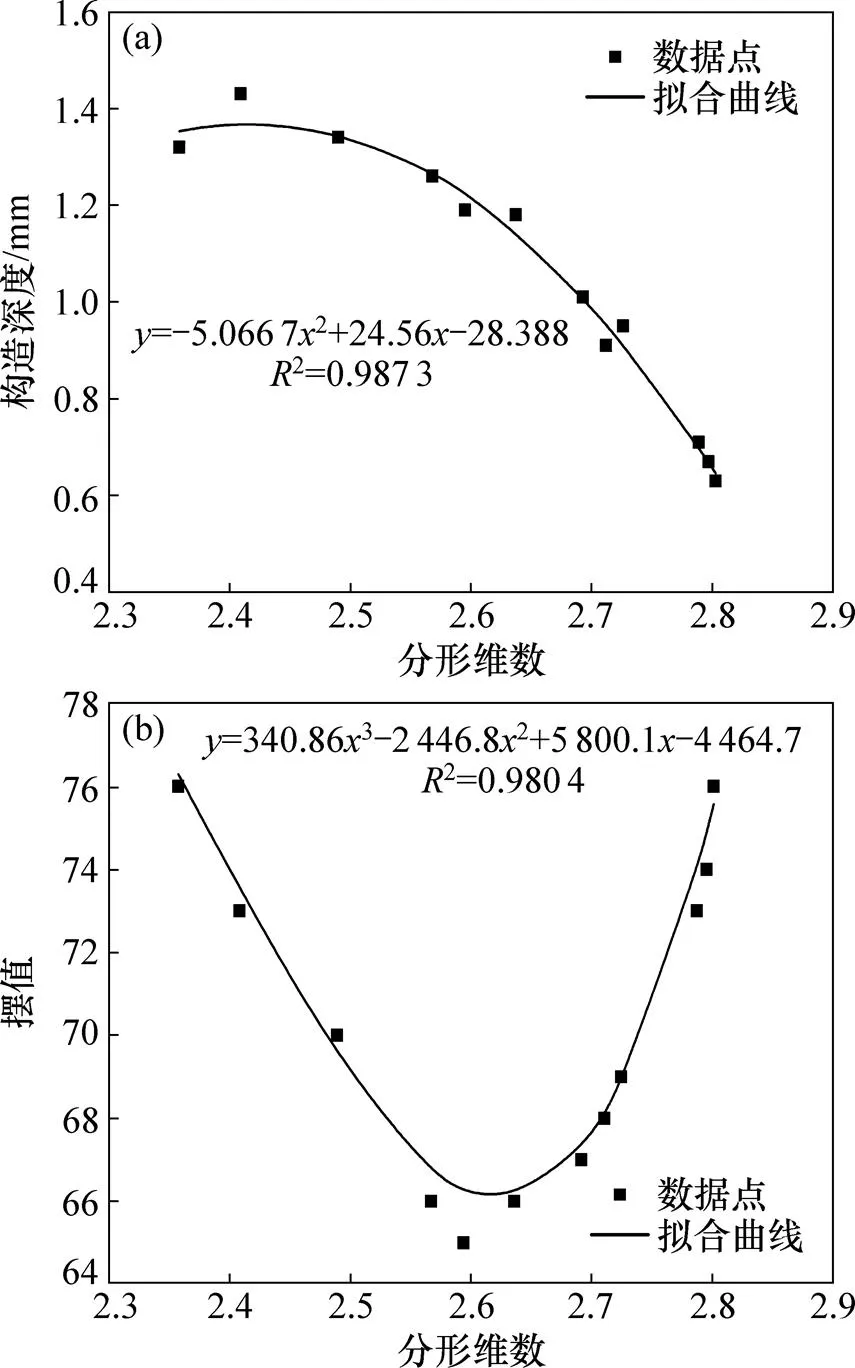
(a) 构造深度与分形维数的关系；(b) 摆值与分形维数的关系

4 结论

1) 根据沥青路面表面的数字图像重构的三维形貌模型，在纹理构造特征上能较好地恢复原沥青路面的表面形貌，可用于分形维数的计算。

2) 针对不同分形维数的分数布朗运动曲面，差分盒维数法的计算结果与理论值最接近，且具有较强的稳定性。

3) 通过差分盒维数法计算的沥青路面表面三维纹理的分形参数误差较小，并且随着集料最大粒径的增大，分形维数表现出变小的趋势，这与实际情况相一致。

4) 沥青路面表面三维纹理的分形特征明显，构造深度随着分形维数的增加而减小，摆值随着分形维数的增加先减小后增加。通过相应的拟合公式可以较好地表征沥青路面的抗滑性能，应用于沥青路面的级配设计及质量监测。

由于试验条件的限制，本文只针对SMA沥青混凝土进行了相关研究，同时没有考虑光照等条件对数字图像提取的影响，因此，数字图像处理技术的普适性还有待进一步研究。

参考文献：

[1] MILLER T, SWIERTZ D, TASHMAN L, et al. Characterization of asphalt pavement surface texture[J]. Transportation Research Record: Journal of the Transportation Research Board, 2012, 2295(1): 19−26.

[2] 童申家,谢祥兵, 赵大勇. 沥青路面纹理分布的分形描述及抗滑性能评价[J]. 中国公路学报, 2016, 29(2): 1−7. TONG Shenjia, XIE Xiangbing, ZHAO Dayong. Fractal description of texture distribution and evaluation of skid- resistance performance for asphalt pavement[J]. China Journal of Highway and Transport, 2016, 29(2): 1−7.

[3] 孙璐, 游克思, 王易阳, 等. 道路因素对车辆侧翻的影响分析[J]. 东南大学学报(自然科学版), 2013, 43(3): 644−648. SUN Lu, YOU Kesi, WANG Yiyang. Influence analysis of road conditions on vehicle rollover[J]. Journal of Southeast University(Natural Science Edition), 2013, 43(3): 644−648.

[4] 杨群, 王胜科, 郭忠印. 二级公路短隧道多孔混凝土磨耗层设计与施工[J]. 建筑材料学报, 2007, 10(4): 473−477. YANG Qun, WANG Shengke, GUO Zhongyin. Application study on open graded cement concrete used in second class short road tunnel[J]. Journal of Building Materials, 2007, 10(4): 473−477.

[5] HORN B K P. Height and gradient from shading[J]. International Journal of Computer Vision, 1990, 5(1): 37−75.

[6] HORN B K P, BROOKS M J. The variational approach to shape from shading[J]. Computer Vision Graphics Image Process, 1986, 33(2): 174−208.

[7] 王端宜, 李维杰, 张肖宁.用数字图像技术评价和测量沥青路表面构造深度[J].华南理工大学学报(自然科学版), 2004, 32(2): 42−45. WANG Duanyi, LI Weijie, ZHANG Xiaoning. Evaluation and measurement of asphalt pavement surface texture depth with digital image technique[J]. Journal of South China University of Technology(Natural Science Edition), 2004, 32(2): 42−45.

[8] 宋永朝, 闫功喜, 隋永芹, 等. 基于数字图像处理技术的沥青路面表面纹理构造分布[J]. 中南大学学报(自然科学版), 2014, 45(11): 4075−4080. SONG Yongchao, YAN Gongxi, SUI Yongqin. Texture structure distribution of asphalt pavement surface based on digital image processing technology[J]. Journal of Central South University (Science and Technology), 2014, 45(11): 4075−4080.

[9] 邹丽琼, 周兴林, 胡怡玮. 基于显微视觉的沥青路面微观纹理三维重构[J]. 武汉科技大学学报, 2015, 38(4): 297−301. ZOU Liqiong, ZHOU Xinglin, HU Yiwei. Three-dimensional reconstruction of asphalt pavement microtexture based on micro-vision[J]. Journal of Wuhan University of Science and Technology, 2015, 38(4): 297−301.

[10] LEONARDI G. Fractal dimension for the characterization of the porosity of asphalt concretes[J]. Archives of Civil Engineering, 2010, 56(4): 321−333.

[11] MALAL K, IGNACIO A, TOM S. Long-term skid resistance of asphalt surfacings: correlation between Wehner–Schulze friction values and the mineralogical composition of the aggregates[J]. Wear, 2013, 303(1): 235−243.

[12] 董祥. 胶粉负载型路面尾气降解复合材料的路用性能[J]. 建筑材料学报, 2011, 14(6): 785−790. DONG Xiang. Pavement performances of composite material with rubber powder loading photocatalyst for pavement automobile exhaust degradation[J]. Journal of Building Materials, 2011, 14(6): 785−790.

[13] MIZUSHIMA A, LU Renfu. An image segmentation method for apple sorting and grading using support vector machine and Otsu’s method[J]. Computers and Electronics in Agriculture, 2013, 94: 29−37.

[14] MOGHADDAM R F, CHERIET M. AdOtsu: an adaptive and parameterless generalization of Otsu’s method for document image binarization[J]. Pattern Recognition, 2012, 45(6): 2419−2431.

[15] OTSU N. A threshold selection method from gray level histograms[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1979, 9(1): 62−69.

[16] CIESIELSKI Z, KAMONT A. Levy’s fractional Brownian random field and function spaces[J]. Acta Scientiarum Mathematicarum, 1995, 60(1): 99−118.

[17] KOEPFLER G, LOPEZ C, MOREL J M. A multiscale algorithm for image segmentation by variational method[J]. SIAM Journal on Numerical Analysis, 1994, 31(1): 282−299.

[18] SARKAR N, CHAUDHURI B B. An efficient differential box-counting approach to compute fractal dimension of image[J]. IEEE Transactions on, Systems, Man and Cybernetics, 1994, 24(1): 115−120.

[19] 杨彦从, 彭瑞东, 周宏伟. 三维空间数字图像的分形维数计算方法[J]. 中国矿业大学学报, 2009, 38(2): 251−258. YANG Yancong, PENG Ruidong, ZHOU Hongwei. Computation of fractal dimension for digital image in a 3-D space[J]. Journal of China University of Mining & Technology, 2009, 38(2): 251−258.

(编辑 陈灿华)

3-D textural fractal dimension and skid resistance of asphalt pavement

QIAN Zhendong, XUE Yongchao, ZHANG Linggang

(Intelligent Transportation System Research Center, Southeast University, Nanjing 210096, China)

The relationship between skid resistance and three-dimensional (3-D) textural fractal dimension of asphalt pavement was studied. At first, four kinds of SMA rut plate specimens were formed and the 3-D textural models of rut plate specimens were reconstructed based on digital image processing technology. According to the measured texture depth, the effectiveness of models was then examined. In the end, the fractal dimension was calculated by differential box-counting method and its relationship with skid resistance was studied. The results show that the reconstructed 3-D textural model accurately restores the surface topography of original asphalt pavement on the textural structure characteristics. The calculated fractal dimension has a good correlation with measured British pendulum number and texture depth, and can well represents the skid resistance of asphalt pavement. The texture depth decreases all the time with the increase of the fractal dimension, but the British pendulum number decreases to the minimum value and then increases.

asphalt pavement; skid resistance; 3-D textural model; fractal dimension

10.11817/j.issn.1672-7207.2016.10.041

U416.217

A

1672−7207(2016)10−3590−07

2015−11−15；

2016−01−20

国家自然科学基金资助项目(51178114)(Project (51178114) supported by the National Natural Science Foundation of China)

钱振东，博士，教授，博士生导师，从事新型道路路面材料研发与应用、桥面铺装及修复关键技术的研究；E-mail：qianzd@seu.edu.cn